不同管径管外含空气/CO2蒸汽冷凝传热特性分析
彭翔, 边浩志, 周书航, 李文涛, 曹夏昕
(1.哈尔滨工程大学 核科学与技术学院, 黑龙江, 哈尔滨 150001; 2.哈尔滨工程大学 黑龙江省核动力装置性能与设备重点实验室,黑龙江 哈尔滨 150001)
当反应堆发生失水事故(loss of coolant accident,LOCA)时,一回路内冷却剂释放到安全壳内形成大量的高温高压气体。为了保证安全壳的完整性,第三代核电机组“华龙一号”设计了能动的安全壳喷淋系统与非能动安全壳热量导出系统(passive containment heat removal system,PCS)[1-5]。在PCS换热器的传热过程中,含大量不凝性气体蒸汽冷凝是影响换热器性能及系统排热能力的关键环节[6-7]。因此,在含不凝性气体蒸汽冷凝研究方面,国内外学者都已经投入了较大精力。Othmer[8]已经发现,在蒸汽的冷凝过程中,引入质量分数为0.5%的空气,就可使冷凝传热系数降低50%。Dehbi[9]通过较大范围的压力变化与不凝性气体浓度变化的实验,拟合出了新的实验关联式。近期,边浩志[10]在收集了Dehbi[9]、Su[11]、Fan[12]等的实验数据后,结合自己的所得到的试验数据,拟合出了一个新的实验关联式。该关联式充分考虑了空气的浓度、压力、壁面过冷度等相关参数的影响,具有较高的参考价值。
现有的研究虽然都涉及到含有不凝性气体的蒸汽冷凝,但是除空气外,其重点都放在了氢气或氦气等气体上。在严重事故条件下,堆芯熔融物与安全壳内的混凝土发生作用(the molten corium-concrete interaction,MCCI),将会产生大量的CO2,CO2扩散至安全壳内,浓度可达10%~20%[13-15],在局部隔间内CO2的浓度会进一步提高。同时,考虑到CO2的分子量为44,大于空气(29)与蒸汽(18)的分子量,也显著大于氢气的分子量(2),这必然对冷凝过程产生不同于氢气的影响。此外,在换热器设计过程中,也会考虑使用不同管径的传热管,因此有必要在不同管径条件下进行含有空气/CO2的蒸汽冷凝传热特性研究。
1 数值计算模型
1.1 基本控制方程
本文基于CFD方法开展数值模拟研究。通过有限体积法对特定的初始条件和边界条件进行守恒方程的计算。主要的守恒方程包括质量守恒方程、动量守恒方程、能量守恒方程以及组分守恒方程,这4种守恒方程的表达式如下:
1)质量守恒方程:
(1)
2)动量守恒方程:
(2)
3)能量守恒方程:
(3)
4)组分守恒方程:
(4)
式中:w为速度矢量;P为表面力,N/m2;f为体积力,N/m2;t为时间,s;E为能量,J;Sm为质量源项,kg/(m3·s);Spv为动量源项,N/m3;Sh为能量源项,J/(m3·s);ω为质量分数;D为扩散系数, m2/s;下角标j表示不同类型的气体。根据Bian[16-17]的研究,本文将使用可实现的k-ε湍流模型进行大空间自然对流的模拟计算。
1.2 冷凝模型
本文所使用的冷凝模型是基于Fick定律的扩散冷凝模型。该模型在实际应用中需要引入相关的源项方程对控制体内的流动与传热过程进行辅助求解。本文所使用混合气体涉及蒸汽、空气、CO2这3种成分,因此,冷凝管近壁面处的蒸汽质量通量为:
(5)
(6)
mcond=mcond,1+mcond,2
(7)
质量源项:
Sm=Sv=mcond/Δ
(8)
式中Dij为混合气体中成分i与j之间的扩散系数,根据Visser[18]的研究,使用下列公式进行计算:
(9)
(10)
(11)
式中:A为常数,0.01 m2/s;T表示温度,K;M表示摩尔质量,kg/kmol;ν表示扩散体积,cm3/mol;P表示压力,Pa;下角标s表示蒸汽,a表示空气,c表示CO2。
Bian[17]考虑到抽吸效应的影响,对气体的分子扩散率进行修正:
Dsa,eff=0.001 43θcDsa
(12)
Dsc,eff=0.001 43θcDsc
(13)
Dac,eff=0.001 43θcDac
(14)
(15)
(16)
θc=2.98+52 000×(7×10-5)θB
(17)
动量源项:
Spv=Smv
(18)
能量源项:
Sh=Smhv
(19)
本文建立的模型中,通过多尔顿分压定律(20)与安托因方程(21)判断蒸汽是否发生冷凝。如果壁面温度低于该蒸汽分压下的饱和温度,则蒸汽在此处发生冷凝。
Pi=XiP
(20)
(21)
式中:Pi为混合气体中某一组分的分压,Pa;Xi为组分气体i的摩尔浓度。
2 计算模型的验证
2.1 几何模型与网格独立性检验
为了进行含空气/CO2的管外冷凝换热研究,以位于哈尔滨工程大学的COAST(condensation and species transport) 装置为原型,1∶1的尺寸建立了本次计算的几何模型。其中气空间的主体为直径1.5 m,高2.1的圆柱体,同时圆柱体的顶部为高度为0.42 m的蝶形封头,筒体壁面与蝶形封头壁面在计算中均设置为绝热壁面条件。传热管壁面为恒壁温边界条件,其直径为19 mm、长1 m,下底面距离气空间底部0.5 m。为了保证计算过程中气空间压力与蒸汽含量相对稳定,将气空间底面设置为质量流量入口,根据User-Defined Function (UDF)计算气空间内蒸汽的冷凝量,并赋值到底部入口,如图1所示。

图1 几何模型Fig.1 Geometry model
为验证网格基本尺寸与网格数量对冷凝换热系数大小的影响,根据上述几何模型,分别采用网格基本尺寸为0.2、0.1、0.08、0.04、0.035、0.03、0.025 m,对系统压力0.4 MPa、冷凝管壁面过冷度40 ℃、蒸汽摩尔分数0.66、CO2摩尔分数0.1的典型工况进行计算,冷凝换热系数h的计算结果如图2所示。
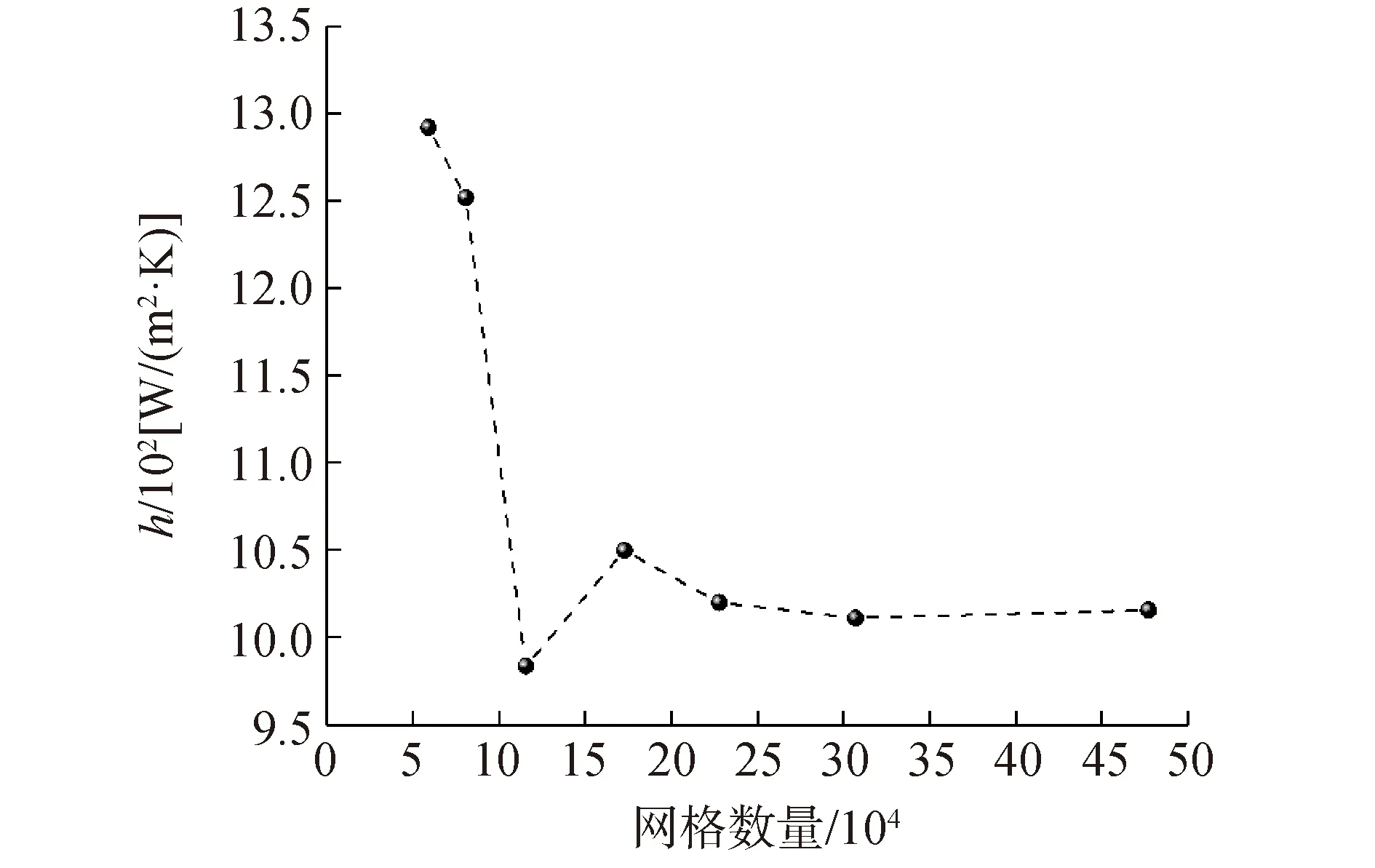
图2 网格独立性检验结果Fig.2 The result for the mesh independence analysis
由图2可以看出,随着网格数量的增加,冷凝换热系数的计算结果逐渐趋于稳定,当网格基本尺寸小于0.04 m,网格数量大于172 480时,网格数量的增大对冷凝换热系数的影响小于5%。结合Bian[5]的研究结果,即主流网格尺寸不应大于0.04 m,本次的网格基本尺寸设为0.03 m,网格数量为303 664。网格实际效果及壁面Y+值如图3所示。

图3 网格划分效果及壁面Y+值Fig.3 Mesh generation effect drawing
由图3可以看出,在此网格条件下,传热管壁的Y+值严格小于5,满足低Y+值壁面处理的要求[13]。
2.2 模型验证
为了验证上述物理模型的可靠性,将模拟计算结果与位于哈尔滨工程大学的COAST 实验数据进行对比,结果如表1所示。由表1可以看出,模拟计算所得冷凝传热系数与试验结果的最大误差小于15%,具有较高的计算精度,后续研究将使用此模型进行计算分析。

表1 冷凝传热系数的试验与模拟计算结果对比Table 1 Comparisons between the experimental and numerical HTCs
3 计算结果及分析
3.1 CO2浓度对高浓度蒸汽冷凝传热的影响
当反应堆发生大破口失水事故时,安全壳内的压力会迅速增大到0.462 MPa的压力峰值。此后,PCS系统投入运行,安全壳内的压力与温度会逐渐降低,最终在0.3~0.4 MPa的范围内小幅波动[19]。因此本文模拟的系统压力设为0.4 MPa,壁面过冷度为40 K,蒸汽的摩尔分数为0.66。在空气中逐渐提高CO2的浓度,不同管径条件下,冷凝换热系数的变化如图4所示。

图4 CO2对冷凝传热系数的影响(Xs=0.66)Fig.4 The effect of CO2 on CHTC in 0.66 steam concentration
由图4可以看出,气空间内只包含蒸汽与空气时,传热管冷凝换热效率较低,冷凝换热系数普遍低于1 000 W/(m2·K)。但在混合气体中加入部分CO2后,传热管的整体换热能力呈现增强趋势,在此工况的极限条件下,即混合气体中只包含蒸汽和CO2时,冷凝换热系数可达到1 220 W/(m2·K),相较于空气,整体换热能力提高了近30%。此外,图中还给出了相同热工参数条件下传热管管径的影响规律。结果表明,随着传热管管径的增大,冷凝换热系数逐渐减小,这与不含CO2条件时的规律相同[20-22]。纵向对比可知,CO2对冷凝换热系数的提升幅度会随管径的增大而增大,12 mm直径传热管在只有CO2与蒸汽条件下的传热系数比空气-蒸汽条件提升了12.37%,而38 mm管径的传热管,提升幅度可达42.27%。
蒸汽浓度为0.66时,近壁面处的蒸汽浓度较高,CO2对蒸汽扩散的阻碍作用较弱。传热管中部(Z=1 m)处的蒸汽浓度分布如图5所示。

图5 传热管近壁面蒸汽浓度分布(Z=1 m)Fig.5 The radial distribution of steam concentration at Z=1 m
从图5可以看出,当气空间内只有蒸汽/空气与只有蒸汽/CO2时,传热管近壁面处的蒸汽浓度分布并未发生显著变化,即蒸汽浓度并未对冷凝传热系数产生显著影响。图6为距离传热管3 mm处气空间的密度与流速分布。

图6 近壁面气体密度与流速分布Fig.6 Gas density and velocity distribution near the wall
由图6(a)可以看出,由于CO2的密度较大,在混合气体中加入CO2后,混合气体的整体密度增大了25%左右,同时,根据理想气体状态方程,CO2较大的分子量使得其密度对温度的变化更为敏感。混合气体中的CO2浓度增大后,气体的密度变化幅度增大,引起了如图6(b)所示的气体流速的增大,进而提高了冷凝传热系数。
3.2 CO2浓度对低浓度蒸汽冷凝传热的影响
在低蒸汽浓度条件下,CO2对不同管径传热管冷凝换热的影响如图7所示。由图7可知,在低蒸汽浓度条件下,高浓度CO2对冷凝换热系数的整体趋势与高蒸汽浓度条件的趋势基本一致。低CO2浓度时,根据式(9)~(17)蒸汽在CO2的扩散系数小于蒸汽在空气中的扩散系数,因此加入CO2后,近壁面蒸汽的扩散能力降低,使得冷凝换热系数由一定程度的降低[23]。但随着CO2浓度的增大,混合气体的密度增大,自然循环能力增强,近壁面的气体流速及湍流程度增大,其促进了蒸汽的对流传质,使得冷凝换热系数逐渐增大,如在19 mm管径传热管上,蒸汽-CO2混合气体的冷凝换热系数较蒸汽-空气的换热系数提高了43.75%。
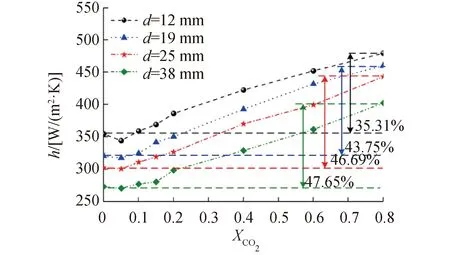
图7 CO2对冷凝传热系数的影响(Xs=0.2)Fig.7 The effect of CO2 on CHTC in 0.2 steam concentration (Xs=0.2)
3.3 CO2浓度对传热管局部冷凝特性的影响
蒸汽摩尔浓度为0.66,不同CO2浓度条件下,冷凝传热系数在传热管上的轴向分布如图8所示。

图8 传热管上冷凝传热系数轴向分布Fig.8 The distribution of CHTC in different CO2 concentration
传热管的位于Z=0.5 m至Z=1.5 m处。从图8中可以看出,在蒸汽与空气的混合气体中引入CO2,并不会对冷凝换热系数在传热管上的轴向分布趋势产生影响。该分布趋势为:在传热管上自上而下,冷凝换热系数呈现先减小后增大的分布趋势。同时,CO2浓度增大后,冷凝换热系数在传热管中部的增长速度也会增大,如由Z=1.30 m至Z=0.51 m,CO2的摩尔分数为0时,冷凝换热系数由881.86 W/(m2·K)增加到987.44 W/(m2·K), Δh=105.58 W/(m2·K);相同高度下,CO2的摩尔分数为0.34时,冷凝换热系数由1 077.37 W/(m2·K)增加到1 448.16 W/(m2·K),Δh=370.79 W/(m2·K)。
图9为不同管径传热管近壁面(距离壁面3 mm)的蒸汽浓度轴向分布。从图9中可以看出,沿传热管自上而下分布,蒸汽浓度都是呈现先降低后升高的趋势,这一分布趋势与冷凝换热系数的轴向分布保持一致。同时,气空间内加入CO2后,冷凝换热系数在传热管中下部的回升幅度显著变大。

图9 传热管近壁面处蒸汽浓度轴向分布Fig.9 The distribution of steam concentration near the wall
在传热管上部,蒸汽接触到冷的传热管壁而发生冷凝,使得该处的蒸汽浓度由主流蒸汽浓度的0.66迅速降低至0.485左右,导致冷凝换热系数减小。而后,随着传热管对气空间的降温沉降作用越来越明显,加之气体流速增大,气体的搅混程度增大,使得近壁面处的蒸汽浓度有所回升(如图9所示),这使得冷凝传热系数也随之增大。同时,由于CO2较大的气体密度与密度变化幅度更大的特性,气空间内存在CO2时,传热管中下段的自然对流强度更大,造成了换热系数在该处较大的回升幅度。
4 结论
1)在相同条件下,传热管的管径越小,冷凝换热系数越大。同时CO2对冷凝换热系数的提升随管径的增大而增大。
2)CO2会通过改变传热管近壁面处的蒸汽浓度与气体流速(气体搅混程度)对蒸汽的冷凝传热特性产生影响。
3)在高蒸汽浓度下(蒸汽摩尔分数为0.66),在空气中加入CO2气体,会通过增大近壁面处的气体密度变化,即增强了大空间自然对流强度,促进蒸汽的对流传质,以显著增大冷凝传热系数,相较于蒸汽-空气,蒸汽- CO2条件下的冷凝传热系数可提高31.37%。
4)在空气中加入CO2不会改变冷凝传热系数在传热管上的轴向分布趋势。冷凝传热系数的轴向分布趋势为:传热管顶部冷凝传热系数最大,随传热管向下延伸,冷凝传热系数先迅速降低而后缓慢增大,且CO2的加入会极大地提升换热系数在中下部的回升速度。

