基于改进粒子群算法的平房仓粮温BP神经网络预测模型建立
王 赫, 曹 毅, 李 玉, 林 琳, 任丽辉, 刘国辉, 周钢霞
(辽宁省粮食科学研究所,沈阳 110032)
我国是粮食生产和消费大国,也是粮食储备大国,粮食作为关乎国计民生的重要战略资源和特殊商品,粮食安全是关系社会经济发展以及国家安全独立的重大战略问题。平房仓一直是我国粮食储藏的主力仓型,特点是仓容大,隔热防潮性能相对较好,并配有粮温检测、机械通风等系统,为安全储粮提供可靠保证。由于仓内储粮体积巨大,而且粮堆传热速度慢,其内部粮食被外围粮食包裹而起到很好的保温作用。但外围粮食受到外界温度变化的影响,会与内部粮食之间存在明显温差,可能会导致局部持续发热的情况出现,加快微生物繁殖生长,最终导致粮食霉变,从而影响粮食的品质,对粮食的储存产生危害[1]。因此,为了保证平房仓内储存的粮食品质,预防不正常粮温的出现,粮食温度的预测模型的研究和应用具有十分重要的现实意义。
近些年来随着人工智能算法的发展,基于智能计算的粮情预测模型也引起了众多科研人员的关注,并取得了一定的研究成果。张忠杰等[2,3]以储粮生态系统、多场耦合和“通风窗口”理论为基础,汇集 WU模型、粮温变化正弦模型和热质传递模型及相关经验模型编制了粮情云图动态分析软件。王传旭等[4]结合Kriging插值和BP神经网络来预测粮仓温度场。张明跃等[5]提出了基于时间-空间相结合的粮温预测模型。黄琦兰等[6]提出了提出一种基于粒子群算法(PSO)和最小二乘支持向量机(LSSVM)的粮情安全性预测模型。
本研究在传统的BP神经网络预测模型的基础上引入改进的粒子群算法对神经网络中的权值和阈值进行不断优化,改进后的粒子群算法拥有更好的局部寻优能力和全局寻优能力,使优化后的BP神经网络能快速的从历史粮温中总结平方仓粮温变化规律,实现平房仓粮温的预测。
1 材料与方法
1.1 数据的采集与整理
本项目实验数据取自辽宁省粮食科学研究所跟踪检测获得的中储粮沈阳直属库实仓温度数据,通过平房仓内的温度监测点实时监控来获取粮仓粮食内部不同位置的温度,其中平房仓内部的温度监测点分布俯视图如图1所示,一共分为4层,每一层有包含104(8×13)个温度监测点。考虑到平房仓内部粮食中间的冷心作用,使得中间位置的粮食受外界环境的影响较小,而粮仓四周的粮食受外界环境的影响较大。本预测模型初步选取的测温点数据分为2个部分,第1部分选取靠近边界的温度监测点(四周墙壁、顶层和底层);第2部分选取的温度监测点位置为中间位置的温度测点。通过对不同位置的温度监测点的粮食温度数据进行训练、预测,来建立不同温度监控点的预测模型,以实现对不同温度监控点位置粮食温度的精确预测。
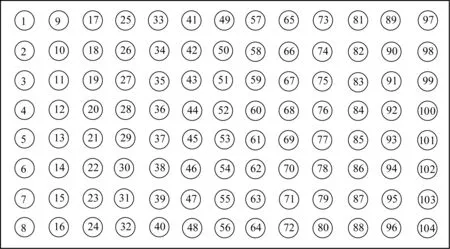
图1 平房仓内部温度监测点分布的俯视图
1.2 历史粮食温度数据的预处理
现取2018年和2019年2个整年的粮食温度的数据,将2018年的粮食温度数据作为训练集建立预测模型,把2019年的粮食温度数据作为测试集来检验模型的预测效果。利用归一化的方法对初始数据进行处理,公式为:
y=(x-xmin)/(xmax-xmin)
(1)
式中:x为输入的粮食温度;xmin和xmax分别为输入的最小值和最大值;y为归一化的输出向量。上式将数据归一化到[0,1]区间内,预测结束后再将数据反归一化为实际数据。
预测模型的输入由是k个历史时刻的粮食温度组成的,通过这些历史数据来预测下一时刻的目标值。下一时刻的真实测量值则作为输入进行滚动预测,以此类推,直到整个时间序列预测完成。模型预测的策略如表1所示。
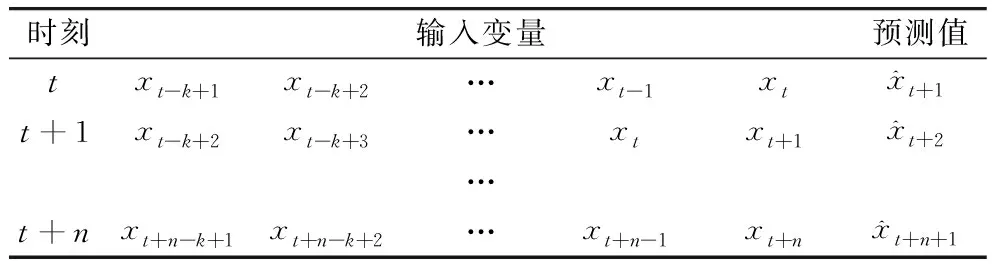
表1 模型预测的策略
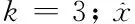
2 粮温预测模型的建立
2.1 建立基于BP神经网络的预测模型
BP(Back Propagation)神经网络全称为误差反向传播神经网络,包含输入层、隐含层和输出层构成。同一层的节点之间互不相连,而不同层之间全部互联,输入层、输出层的节点数的选取通常取决于输入及输出向量的维数,隐含层节点数目没有明确的规定,通常根据实际情况来确定。BP神经网络具有能逼近任意一个非线性映射函数的特性,且无需建立数学解析式模型,因此在预测方面的应用最为广泛。其网络结构如图2所示[7-10]。

图2 BP神经网络内部结构图
BP神经网络是将训练出的所有信息以神经元节点权值和阈值的形式存放在训练网络中,通过正向传播和反向传播不断迭代,从而使该网络有较好的自学习效果和泛化能力[11-15]。预测模型将2018年平房仓粮食温度的数据作为训练集,通过设定初始的阈值和权值以及一定数目的迭代次数来训练BP神经网络来获取预测模型,在第t次迭代的正向传播中,其隐含层的第j个神经元的输出结果为:

(2)

(3)
其中选取的激励函数f为Sigmoid函数:
(4)
则其第t+1次迭代的反向传播为:
(5)
(6)
(7)
式中:xi为第i个输入;ω为连接权值;α和β为阈值;Ij为第j个隐含层输出;M和N为隐含层和输出层神经元个数;yk为第k个输出层神经元的输出;ek为第k个输出层神经元的输出误差值。
2.2 粒子群算法的改进
粒子群优化算法(PS0)是一种基于群体智能理论的优化算法,首先通过优化一群粒子,然后不断迭代并跟踪当前最优的粒子来搜索最优值。设多维搜索空间中,存在m个粒子构成一个群体,在第t次迭代中,第i个粒子的速度和位置为Xi,t和Vi,t,粒子通过2个最优解来更新自己的合适位置和速度。这2个最优解分别为粒子自身找寻的最优解即个体极值Pi和整个种群当前找寻的最优解即全局最优解Gi。在迭代过程中,粒子通过公式进行更新自己的速度和新的位置:
Vi,t+1=w·Vi,t+1+c1·rand·(Pi-Xi,t)+c2·rand·(Gi-Xi,t)
(8)
Xi,t+1=Xi,t+λ·Vi,t+1
(9)
式中:w为惯性权重;rand为[0,1[之间的任意随机数;c1和c2为学习因子;λ为速度系数并且λ=1。
由于基本的粒子群算法的收敛速度和全局寻优能力有限,本温度预测方法提出用非线性变化的惯性权重来代替固定的惯性权重来提高粒子群算法的性能。新的非线性变化的惯性权重表达式为:
(10)
式中:wmin和wmax分别为惯性权重w的最小值和最大值;t为当前迭代次数;tmax为最大迭代次数。当t较小时,w接近于wmax,并且w的减少速度也较慢,这保证了粒子群算法的全局寻优能力;随着t增大,w以非线性变化递减且w的减少速度加快,提高了粒子群算法的局部寻优能力,从而使改进的粒子群算法能更灵活地调整局部寻优能力和全局寻优能力。
2.3 平房仓粮温预测模型的建立
利用改进的粒子群算法优化的BP神经网络具体建模流程图如图3所示。该流程图主要包括:BP神经网络的结构构建、改进的粒子群算法优化BP神经网络权值和阈值以及BP神经网络训练和预测。具体步骤为:设计BP神经网络各层神经元节点数。本预测模型设置BP神经网络输入层神经元个数为3;隐含层神经元个数设置为10;输出层神经元个数为1。

图3 粮食温度预测模型的流程图
将BP神经网络的初始权值和阈值转化成粒子群算法中的粒子,随机初始化粒子的速度Vi和位置Xi,将预测结果与实际值的平方和作为适应度值。

(11)

通过改进的粒子群算法计算个体和全局的最优极值。
Vi,t+1=w·Vi,t+1+c1·rand·(Pi-Xi,t)+c2·rand·(Gi-Xi,t)
(12)
Xi,t+1=Xi,t+λ·Vi,t+1
(13)

(14)
式中:w为惯性权重;rand为[0,1[之间的任意随机数;学习因子c1=c2=2,最大和最小的惯性权重分别为wmax=0.9;wmin=0.1;λ为速度系数并且λ=1;最大迭代次数tmax=2 000;t为当前迭代次数。
将第3步经过改进的粒子群优化算法得到的最优极值即最优初始权值和阈值矩阵代入BP神经网络公式中:
(15)
(16)

(17)
建立BP神经网络,参数设置如表2所示。用平房仓2018年历史数据作为训练数据,2019年平房仓温度测试数据作为测试数据分别对神经网络训练和测试,并将改进的BP神经网络温度预测模型的输出预测结果和2019年的实际温度测量数据进行对比,预测模型建立完成。

表2 BP神经网络参数设置
3 结果与分析
根据预测模型及方法,选取位于粮堆不同位置和深度具有代表性的温度监测点进行温度预测并将预测结果与传统BP神经网络预测结果进行对比,图4和图5分别为平房仓第1层1号、平房仓第3层1号测温点温度预测结果对比图。根据预测结果可知,与实际温度相比,平房仓第1层1号测温点的BP神经网络温度预测结果在初始时刻及末端时刻的预测结果误差较大,且预测结果具有一定程度的波动。结合图5中平房仓第3层1号测温点温度预测结果可知,改进后的粒子群算法优化后的BP神经网络预测误差更小,整体预测结果与实际粮食温度趋势吻合,而传统BP神经网络预测结果中具有较大的顶峰误差,且预测结果的波动程度更高,稳定性较差。

图4 平房仓第1层1号测温点温度预测对比曲线(2019年数据)
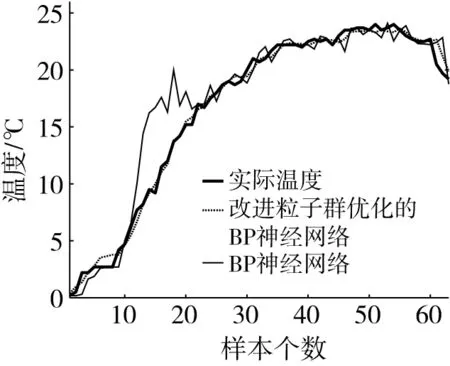
图5 平房仓第3层1号测温点温度预测对比曲线(2019年数据)
为了对比预测模型与BP神经网络预测的效果,保证预测结果的精确性和可靠性,在粮食温度预测效果的评测上,选取平均绝对误差(MAE)和均方根误差(RMSE)来表示。

(18)

(19)


表3 预测模型与BP神经网络预测误差对比
由此可知,预测模型能够更好地实现不同传感器位置下粮食温度的精准预测,其预测结果误差更小,预测曲线与实际温度分布曲线更加吻合。同时,在预测过程中,改进后粒子群算法优化的BP神经网络的初始及末端时刻预测误差更小,预测过程中的波动程度及顶峰误差更低。
4 结论
提出了一种基于改进后的粒子群算法优化BP神经网络的粮食温度预测方法。针对平房仓内部不同温度监测点处的粮食温度建立预测模型对仓内不同位置的粮食温度进行细化,利用改进后粒子群算法强大的局部及全局寻优能力,优化BP神经网络的权值与阈值,可以更精确地定位到不正常粮温出现的位置,较传统的BP神经网络预测拥有更精确的预测精度,更小的预测误差,实现平房仓内不同温度监测点处粮食温度的精准预测。通过改进后的粒子群算法优化BP神经网络,能够提升不同温度监测点处的粮食温度的预测精度,降低传统BP神经网络预测中的顶峰误差,提升预测结果的平滑性。与传统BP神经网络相比,该算法在各传感器处的粮食温度预测精度均有一定的提升,提升程度最大的为75号第3层,其均方根误差降低约1.075,平均绝对误差降低约1.829。改进后粒子群算法优化的BP神经网络预测结果能够更好地学习粮食温度的数据特征,预测结果更加吻合实际粮食温度数据,对实际工程应用具有重要意义。

