基于相场方法的多孔合金马氏体相变模拟*

李腾 邱文婷 龚深2)†

1) (中南大学材料科学与工程学院,长沙 410083)

2) (中南大学粉末冶金国家重点实验室,长沙 410083)

相比块体材料,多孔材料中孔洞的存在影响形状记忆合金马氏体相变的演化过程,包括马氏体变体形貌、分布以及自协调效应.实验结果表明,引入金属-空气界面可以细化马氏体变体组织,从而可提升合金的阻尼性能.本文在实验观察中发现界面周围没有出现马氏体变体的浮凸,且存在非相变组织,分析认为多孔材料中存在的金属-空气界面并不是自由表面.基于与时间相关的金茨堡-朗道方程构建了不同界面约束下的三维相场模型,研究了多孔材料中约束界面对马氏体变体自协调效应的影响.在金属-空气界面附近模拟得到了细小的马氏体变体自协调形貌,与实验结果一致.在界面约束条件下,体系主要以降低应变能的方式实现总能量的最小化.不同界面条件下的模拟结果表明,提高多孔材料的比表面积是得到更多细小马氏体变体组织的有效手段.

1 引言

形状记忆合金中存在具有不同位向关系的马氏体变体,在外界存在周期性应力时,变体间的孪晶面发生移动并重新排列,以非弹性应变的方式实现能量松弛,外部振动通过界面处的摩擦而损耗,从而实现阻尼效应[1-5].研究表明,当金属内部孔隙达到一定密度时,样品的力学性能将有所牺牲,但会提升样品的阻尼性能以及能量吸收能力[6-8].多孔形状记忆合金同时具备多孔结构与马氏体相变属性,从而具有较好的阻尼减振性能.

多孔形状记忆合金的阻尼性能已得到了许多验证[7-10].但相比块状形状记忆合金,多孔材料中存在着大量微米级或纳米级的孔隙,以及形状各异的金属-空气界面.界面在空间上阻断了合金马氏体相变的连续性,破坏了马氏体变体间的自协调效应[11,12].因此马氏体相变在多孔合金界面处受到约束,使得块体马氏体相变规律无法直接应用于多孔材料中.

目前针对马氏体相变的组织结构模拟方法主要包括分子动力学(MD)[13]和相场方法(PF)[14]等.其中分子动力学是从原子尺度出发,通过计算体系内各粒子的相互作用势,从而建立一组运动方程并对其进行求解,因而适用于几纳米到几十纳米的三维空间尺度,在介观领域中的模拟上略有不足,常应用于纳米晶马氏体相变的模拟[15,16].而相场方法最大的特点是扩散界面的定义,使得在微结构演化过程中不需要通过数学方程明确跟踪界面位置.因此,可以预测相变过程中观察到的复杂晶粒形态的演变,而无需对晶粒形状进行任何先验假设.相场方法通过一组在时间与空间上连续的相场变量动力学方程来分析微观结构的演变过程,其演化驱动力来源于系统总自由能的降低,为进一步研究其界面约束的包括局部化学能、梯度能、弹性能以及由于磁场或静电作用带来的其他能量.同时相场方程具有唯象的特点,基于一般热力学和动力学原理可导出相场变量的演化方程,而无需对单个原子分子进行处理.其计算尺度通常为纳米和微米级,适用于介观尺度下的模拟[17-19].

金属-空气界面在此前的相场研究中被认为是自由表面,即马氏体相变产生的应变能可以在此处通过变形浮凸的方式释放,马氏体能垒因此得以降低,并促进了马氏体相变的进一步发生[20-22].在Song 等[23]的研究中,自由表面附近的马氏体相变完成时间更短,残余奥氏体含量相比非自由界面(约束界面)更低,Malik 等[24]的研究同样表明,自由表面下的马氏体变体间的厚度相比约束界面下有所增大,变体与变体间的界面数量降低.这是因为马氏体与母相由于切变与晶格畸变产生的应变能在自由表面处释放,因此相变引发的应变能仅存在于变体板条的边界,为进一步降低系统总能,变体间的边界数量将会有所减少[25,26].但如果将多孔形状记忆合金中的金属-空气界面理解为自由表面,即使是在孔隙率仅40% 的多孔形状记忆合金中,马氏体相变的应变能也会得到充分的释放.而在马氏体的逆相变过程中,相变驱动力是原本作为阻力的应变能,由于应变能在前一阶段没有积累,按照自由表面理论,马氏体的逆转变将无法发生[26],这与事实是矛盾的.

本文通过烧结蒸发工艺[27]制备了多孔CuAlMn形状记忆合金.合金发生马氏体相变后,金属-空气界面平滑连续,没有观察到马氏体的浮凸现象,并且在界面周围观察到非相变组织.因此可认为在多孔合金中,金属空气界面是非自由表面,即马氏体无法在此处释放积累的应变能.为进一步分析非自由界面对多孔形状记忆合金马氏体相变的组织结构影响,本文以Cu-11.9Al-2.5Mn 合金为例,通过3D 相场模拟计算了该合金在非自由表面约束下的马氏体相变微结构演化过程,以及马氏体生长过程中的自由能密度变化.结合TEM 分析,揭示了马氏体的自协调效应在金属-空气界面约束下的影响,并对可能出现的其他界面类型下的马氏体相变的形貌、组织变化进行预测以及自由能密度分析.

2 三维相场模拟

2.1 化学能

系统中总的自由能E被认为由两部分组成,即化学能Echem与弹性能Eelast[28].其中化学能由系统热力学性质决定的局部化学能和描述界面能量的梯度能组成[21]:

其中,f0表示奥氏体的化学自由能,通常被设置为0.而 Δf(T) 代表在T温度下,奥氏体转变为马氏体的局部化学能密度的变化,可以通过相变潜热Q,以及相平衡温度T0求得:

{ηi}=η1,η2,···,ηp是相场模拟一组描述马氏体(有序)状态的序参量,其中n为变体的数量.这n个定义在0 到1 之间的连续场变量η1,η2,···,ηn,描述马氏体相变中奥氏体与马氏体的状态.母相奥氏体对应的序参量η1=η2=···=ηn=0 的情况,而马氏体变体i对应着ηi=1而ηj=0 ,其中ηj ∈{η1,η2,···,ηn}(j/=i).方程中A,B,C,D是描述局部化学自由能密度方程的形状常数,本文取A=1,B=15,C=7,D=7.βij(p) 为正定二阶张量,r为空间坐标.本工作假设界面能是各向同性的,即βij(p)=βδij,其中β是正常数,δij是克罗内克符号.

2.2 弹性能

在马氏体相变过程中,弹性能来源于马氏体与母相间由于晶格畸变所产生的应变能,是应力状态与马氏体分布状态共同作用的结果.在相场模型中,应变能对自由能的贡献可以通过序参量{ηi}计算得出.在单晶完全约束条件下(即假设εa=0),根据Khachaturyan[29]的微弹性理论,系统的总弹性能Eelast可以表示为

其中,cijkl是弹性模量张量是变体p对应的无应力应变张量,即在无应力状态下,达到平衡态时晶格的Bain 畸变的应变大小.其中符号〈···〉为

2.3 动力学方程

在相场模型中,马氏体相变的演变过程由时间相关的金茨堡-朗道 (Time Dependent Ginzburg-Landau,TDGL) 方程控制[30,31]:

其中,Etotal是系统总能量,是系统化学能与弹性能之和.L为动力学系数,通常取1,在本文孔洞模拟中将孔洞内部的动力学系数L设置为0,使孔洞不直接参与马氏体相变.式中ξp(r,t) 是Langevin 噪声项,在时间和空间维度上都是均匀的,并且符合涨落耗散定律的要求[31],因此满足

式中,kB是玻尔兹曼常数,δ(r-r′)是德尔塔函数.

通常为计算方便,对系统的动力学方程在数值求解时,需要对时间于在单位上进行归一化,即无量纲处理以消除不必要的参数.定义为无量纲时间,无量纲空间坐标=r/l0,其中l0是晶格单元的长度.因此无量纲处理后的相场动力学方程为

3 相场模拟的参数

本文以Cu-11.9Al-2.5Mn 合金的DO3→M18R马氏体相变为例,通过相场方法研究其马氏体相变过程中变体自协调效应受多孔合金中孔洞界面的影响,以及在其他类型孔洞界面下的微结构演化过程和自由能变化情况.由马氏体晶体学的对称性可知,M18R 马氏体相变中独立的变体最多有12 个,分别对应12 种无应力应变张量3,···,12),由下式给出:

其中,β,ρ,τ,σ是与晶格畸变有关的常数,由母相和马氏体的晶格常数决定.Cu-11.9 Al-2.5 Mn合金的马氏体晶格常数[32]a=0.4475 nm,b=0.5229 nm,c=3.815 nm,β=89.6°.通过文献[33]中的计算方法可以得到ρ=0.24548,β=-0.19167,τ=0.01237,σ=0.05511,为简化计算,本研究选择以4 变体代替12 变体进行计算.

在Cu-11.9Al-2.5Mn 合金中,E=120 GPa,v=0.3,As=315°,Ms=210°[34],因此相平衡温度T0=(Ms+As)/2=262.5 ℃,相变潜热Q=3.75×107J/m3[35],过冷度为100 ℃.模拟中无量纲梯度能系数,动力学常数L=1 .在本研究中网格单元长度l0可以通过计算得出,式中γ为界面能量密度,取γ=21 mJ/m2[36],因此得到l0=2.25 nm.经试验得,时间步长取0.01 时,具有能使得模型收敛的同时具有足够的精确性,总步长取20000,即=200 .相场模型在NVIDIA GeForce RTX 3090中以Python 代码的方式实现.

4 实验结果与讨论

为验证多孔形状记忆合金在阻尼减震中的优异性能,制备了块状Cu-11.9Al-2.5Mn 合金以及多孔Cu-11.9Al-2.5Mn 合金.块体的CuAlMn 合金P2'内耗峰峰值为0.2,当孔隙率达到45%时,内耗峰增大达到0.22 左右,多孔CuAlMn 合金的相变内耗峰峰值随着孔隙率的增大而增大.多孔形状记忆合金之所以能提升更高的阻尼性能,除了孔洞结构相较于块体结构能在周期性振动条件下导致的基体应力、应变分布不均,进而产生畸变和膨胀而耗散能量外,还包括多孔结构中丰富的金属-空气界面对马氏体相变的组织约束作用.为进一步研究界面约束对马氏体组织形貌的影响,对两种结构的CuAlMn 合金进行TEM 观察,其中图1 分别是对块状的CuAlMn 形状记忆合金以及通过烧结蒸发工艺制备得到的多孔CuAlMn 形状记忆合金的TEM 照片,以及对应的组织示意图.从图1 得知,两者均观察到了平行的马氏体变体条纹,变体条纹边界清晰,厚度相对均匀.块状的CuAlMn 合金中马氏体变体条纹尺寸在60—120 nm 之间,而多孔CuAlMn 合金中马氏体变体条纹尺寸为20—50 nm.相较于块体合金,多孔合金的马氏体变体条纹明显细化,出现了更多马氏体-马氏体界面.进一步观察发现,在多孔合金中的金属-空气界面并没有因为马氏体相变导致的表面浮凸出现界面的变形.相反,从图1 观察到,孔周围存在一个尺寸在10 nm左右(最薄处为5 nm)的非马氏体组织.金属空气界面处的非相变组织阻碍了马氏体相变的进一步进行,由于其无法发生马氏体相变,使得非相变组织所在的影响区域无法参与马氏体变体的自协作效应中,阻碍了系统自由能调节,从而约束了基体组织的马氏体相变行为.

为研究界面约束对马氏体结构的影响,建立基于TDGL 的相场动力学方程,对CuAlMn 合金的马氏体相变动力学进行了模拟.无界面约束下的CuAlMn 形状记忆合金的马氏体相变相场模拟结果如图2 所示,与块体合金相对应.图2(a)所示为20000 步长下的3D 模拟组织形貌结构,其中不同颜色所代表的四变体呈现自适应结构,边界清晰,马氏体变体条纹平行与母相(110)晶面,这与铜基形状记忆合金的发生马氏体相变时的晶体学位向关系相符.图2(b)是图2(a)中水平方向的2D切面,在二维视图中可观察到变体条纹厚度约为100 nm,与图1(a)中观察到的尺寸基本一致.图2(c)为各变体在各步长下的含量变化,可根据其含量变化方式分为3 个阶段: 形核期(0—2000 步长)、长大期(2000—4500 步长)以及稳定期(4500 步长后).在进入稳定期后,马氏体总含量已接近100%,各变体含量趋于稳定,变体间的边界在此阶段逐渐清晰.观察到在模拟结果中,各变体含量基本接近,符合块体马氏体变体生长的动力学规律.对比模拟结果与CuAlMn 马氏体TEM 照片,可以认为在无界面约束的块体合金中,马氏体相场模拟形貌与实际形貌基本符合.

为探究金属-空气界面处非相变组织对马氏体相变的影响,解释多孔合金中马氏体变体条纹细化的原因,在相场模型中金属-空气界面内的组织以相场动力学系数设置为0 的方式设计为非相变组织.从而使得此区域无法发生马氏体相变,同时也不会产生马氏体相变的相变应变,因此非相变组织与金属基体间存在受材料连续性约束的非自由表面.图3 为非自由界面约束下CuAlMn 合金马氏体相变的相场模拟结果,图3(a)是非自由界面示意图,球形的非相变组织置于模拟单元的中心,其界面半径为135 nm.相场模拟的3D 结果如图3(b)中所示,可以观察到四变体的自适应结构,与无界面约束下马氏体形貌模拟结果相比,界面约束下的马氏体条纹明显细化,变体间界面数量明显增多,但变体仍保持相互平行的形貌,同时边界清晰.图3(c)为非自由界面约束模拟中其各变体的含量的变化,形核期和长大期阶段基本符合无界面约束下的马氏体相变的模拟规律.而在稳定期,非自由界面约束下的马氏体变体两两一组,彼此间在含量上具有较为明显的差异.图3(d)对应图3(b)中的水平2D切面,从切面中可以观察到在界面约束下的马氏体变体条纹厚度均匀,约为34 nm,这与在图1(b)中的TEM 观察结果相符.

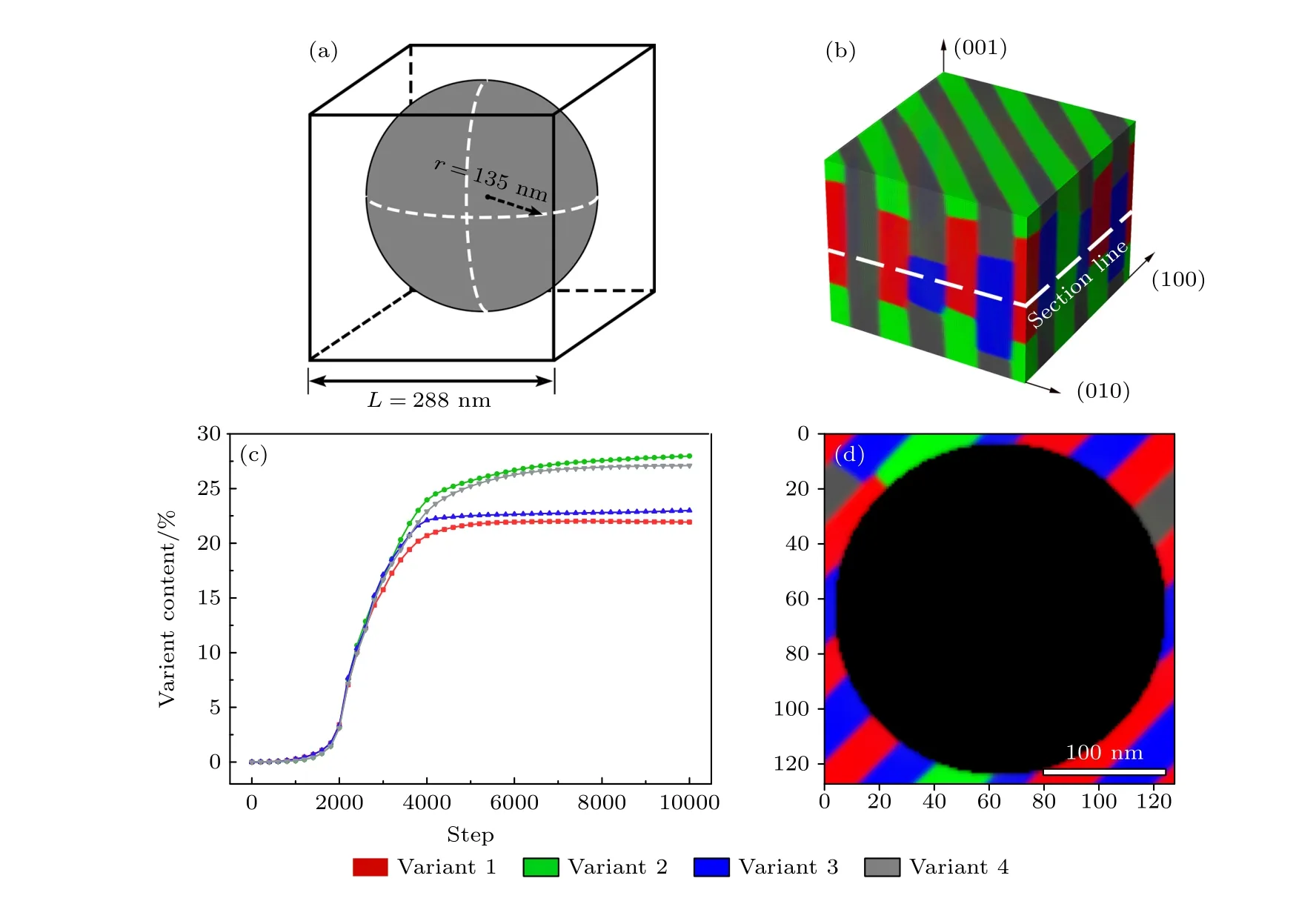
图3 CuAlMn 合金在非自由界面约束下的马氏体相变相场模拟结果 (a)模型中的非自由界面示意图;(b) 20000 步长下的3D 模拟照片;(c)各变体含量随模拟步长的变化;(d) 20000 步长下的2D 模拟切面Fig.3.Phase-field simulations of CuAlMn martensitic transformation under non-free interface constraint: (a) Schematic diagram of non-free interface in the model;(b) 3D simulation image at 20000 steps;(c) content of each variant with simulation step;(d) 2D simulation section at 20000 steps.

导致马氏体变体条纹细化、界面增加以及各变体含量不均匀性提高的原因是多孔材料中金属-空气界面的引入.在金属-空气界面周围的非相变组织无法参与马氏体相变,阻碍了变体自适应结构在界面处的形成,限制了变体间的应力调节作用,因此在界面附近无法形成如图2 中的理想的四变体自协调形貌.受材料连续性影响,界面处的非相变组织对周围母相的马氏体相变具有约束作用,从而导致其周围形成的马氏体的平均自由能相对于无界面约束下的马氏体有所提高.

为进一步从能量角度分析金属-空气界面对马氏体相变带来的影响,通过(1)式与(3)式计算了不同约束条件下的马氏体整体平均自由能密度变化,以及局部自由能密度分布情况,如图4 所示.设图2(a)中的无界面约束下的马氏体相对于母相的整体平均自由能密度变化为-E0(E0>0) .图4是2D 水平切面处的组织形貌与自由能密度分布结果,其中图4(a),(b)是在图2(a)的模拟结果中添加了半径为r=135 nm 的非相变组织后,呈现的新的组织形貌以及自由能密度分布.在对无界面约束的模拟结果中添加非相变组织后,其整体平均自由能密度上升至-0.66E0.图4(c),(d)为图3(d)所对应的非自由界面约束下的组织形貌以及自由能密度,其整体平均自由能密度为-0.81E0.可以发现在多孔材料中非自由界面的影响下,模拟单元的整体平均自由能相对于块体材料无界面约束下的马氏体有所上升,这表明界面的存在提高了材料整体的能量.

图4 CuAlMn 合金在非自由界面约束下的水平切面形貌及自由能密度分布 (a),(b)在无界面约束的模拟结果(图2)中添加非相变组织后的形貌及自由能密度分布;(c),(d)非自由界面约束下的形貌及自由能密度分布.其中(b),(d)中的颜色代表自由能的相对大小(下同)Fig.4.The morphology and distribution of the free energy density of CuAlMn alloy in horizonal section under non-free interface constraint: (a),(b) Morphology and free energy density distribution with non-transformed structure added in the simulation results without interface constraints (Fig.2);(c),(d) morphology and free energy density under non-free interface constraint.The color in(b) and (d) represents the relative size of free energy density (the same below).

通过对图4(a),(b)与图4(c),(d)中,具备相同非相变组织下不同变体组织结构的平均能量的对比,说明在非自由界面的影响下,图4(c),(d)中所对应的变体条纹厚度小、马氏体-马氏体界面数量多的结构,在能量角度上更加稳定.在本文的相场模拟中,系统的能量由局部化学能、梯度能以及应变能组成,马氏体-马氏体界面数量的增加会带来梯度能的提升.而在化学能基本没有改变的情况下,图4(c),(d)相比图4(a),(b)具有更低的平均自由能密度,从能量角度分析这是由于应变能的下降.可以认定在非自由界面的影响下,尽管较细的变体条纹会带来更大的梯度能,但有助于在变体的自协调过程中降低体系的应变能,从而使得整体能量达到更加稳定的状态.从图4(b),(d)中自由能密度分布情况可以发现,相对于细化的变体组织,在界面处周围具有较厚变体条纹的图4(b)中,马氏体变体内部出现了更大比例的高能态区域.在这些区域内无法实现马氏体变体的自协调,从而累积了较大的马氏体转变应力,并有进一步转化为其他变体的趋势.在图4(d)中仅在部分变体间、约束界面周围分布了高自由能密度区域,在能量角度具有稳定性.这进一步说明了在金属-空气界面影响下,细密的变体条纹具有相对稳定的结构.

非相变组织与基体形成的非自由表面在CuAlMn 合金的马氏体相变中会细化界面周围马氏体变体的自协调条纹,为进一步探究在相对远离非自由表面的组织的马氏体相变行为的差异性,在相场模型中设计了不同半径的非相变组织.图5 是对CuAlMn 形状记忆合金在局部非自由界面约束下的马氏体相变的相场模拟结果,包括马氏体的形貌、变体含量变化以及水平切面中自由能分布情况.图5(a),(b)是非自由表面在模拟单元中的示意图,其半径为67.5 nm.

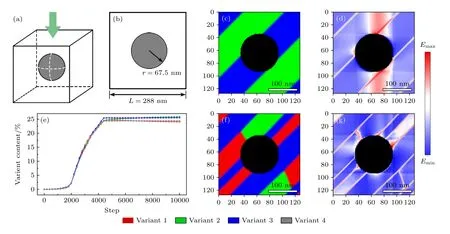
图5 CuAlMn 合金在局部非自由界面约束下的马氏体相变相场模拟 (a),(b)模型中的局部非自由界面示意图;(c),(d)在无界面约束的模拟结果(图2)中添加局部界面约束后的水平切面形貌及自由能密度分布;(e)各变体含量模拟结果;(f),(g)局部界面约束下的水平切面形貌及其自由能密度分布Fig.5.Phase-field simulations of martensitic transformation of CuAlMn alloy under localized non-free interface constraint: (a),(b) Schematic diagram of localized non-free interface in the model;(c),(d) morphology and free energy density distribution in horizonal section with localized non-free interface added in the simulation results without interface constraints (Fig.2);(e) content of each variant with simulation step;(f),(g) morphology and free energy density in horizonal section under localized non-free interface constraint.

在图5(f)马氏体形貌的2D 截面中可以观察到,马氏体变体条纹只在非自由界面周围的影响区域出现了较细的条纹,约为33 nm,而在远离非相变组织的区域变体条纹厚度约为70 nm.局部非自由界面约束下的马氏体变体含量在达到稳态后,与图3(c)中非自由界面约束下的模拟结果类似,各变体含量呈现一定差异,但含量不均匀性相对较小.

上述现象是因为非相变组织的尺寸降低,界面对整体的平均影响也随之减弱,界面对组织马氏体相变的影响主要体现在界面周围一定范围内的影响区域,在界面影响区内金属基体受到界面的约束,马氏体变体条纹通过细化以降低系统总能.而在远离界面的区域,界面对组织的约束力相对较小,其形貌规律则与无界面约束条件下的马氏体形貌相符.因此如图5 所示的局部非自由界面约束的马氏体相变模拟结果,在总体变体含量不均匀性方面介于非自由界面约束与无界面约束的结果之间.

图5(c),(d)是在无界面约束下的模拟结果中添加了如图5(a)所示相同大小的非相变组织,通过新的组织结构计算得到的自由能密度分布情况,其相对于母相的平均自由能密度变化为-0.89E0.而图5(f),(g)为局部非自由界面约束下的CuAlMn马氏体相变的形貌与能量分布情况,其平均自由能密度变化为-0.95E0,相比前者不仅在平均能量上有所降低的同时,高自由能密度区域的分布也局限于部分边界处.可以认为,局部的非相变组织(非自由界面)只在一定范围内的影响区域中约束变体自协调条纹的尺寸,这种协调关系虽一定程度增大了系统的梯度能,但使应变能降低从而降低整体的平均自由能,使合金达到稳定状态.

多孔材料中由于孔洞分布具有一定随机性,通常会出现由多孔组成的复杂非自由表面约束体系,因此在复杂界面下的马氏体会同时受到多个界面产生的约束.为进一步探究多重界面对马氏体形貌及其生长规律的共同约束机制,在相场模型中引入了一组单个半径为72 nm 的双重非自由界面.图6(a),(b)展示了TEM 中双孔处的马氏体形貌,可以观察到在孔间马氏体变体平行条纹厚度为30—70 nm,相较于其他区域厚度较小.金属-空气界面边界连续且清晰,马氏体在此处没有形成浮凸,同时在界面处观察到与图1(b)类似的非相变组织.双孔非自由界面在模型中放置的位置如图6(d),(e)所示,图6(c)是双重界面约束下的3D 模拟结果,可以观察到变体条纹总体平行.在水平切面图6(f)中可以观察到,在双重界面共同影响的区域的变体条纹厚度约为36 nm.从图6(g)中的含量变化上分析,变体间含量存在局部差异,不均匀性介于界面约束(图3)模拟结果与局部界面约束(图5)模拟结果之间.从形貌上看,双孔界面影响下的马氏体形貌与局部非自由界面约束下的马氏体形貌类似,即在界面影响区域内变体条纹较细小,而远离孔影响区的条纹相对较粗.为进一步从能量角度分析双重界面约束下的马氏体组织形貌构成,对比了在同类型双重界面约束下的不同形貌的马氏体变体组成的自由能密度分布情况.如图7(a),(b)所示,在向无界面约束的模拟结果中添加双重非相变组织后,在界面周围变体内大部分区域均表现出较高自由能密度,系统平均自由能密度变化为-0.78E0,整体上来说能量是不稳定的.而在图7(c),(d)所示的马氏体变体构成模式下,界面共同作用区间出现能量稳定区域.系统平均自由能密度变化为-0.93E0,在数值上接近于图5 所对应的局部非自由界面约束下的系统能量变化.双重界面约束体系并没有因为界面数量的增加导致系统自由能变化同比例增大,这是双重非自由界面对孔间组织共同作用的结果.

图6 CuAlMn 合金在双重非自由界面约束下的马氏体相变 (a),(b)TEM 照片;(c)20000 步长下的3D 模拟照片;(d),(e)模型中的孔洞示意图;(f) 20000 步长下的2D 模拟切面;(g)各变体含量模拟结果Fig.6.Martensitic transformation of CuAlMn alloy under the double non-free interface constraint: (a),(b) TEM images;(c) 3D simulation image at 20000 steps;(d),(e) schematic diagram of double non-free interface in the model;(f) 2D simulation section at 20000 steps;(g) content of each variant with simulation step.

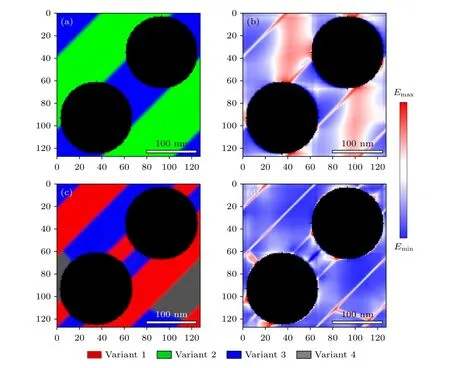
图7 双重非自由界面约束下水平切面形貌及自由能密度分布 (a),(b)在无界面约束的模拟结果(图2)中添加双重界面约束后的形貌及自由能密度分布;(c),(d)双重界面约束下的形貌及自由能密度分布Fig.7.The morphology and distribution of the free energy density in horizonal section under double non-free interface constraint:(a),(b) Morphology and free energy density distribution with double non-free interface added in the simulation results without interface constraints (Fig.2);(c),(d) morphology and free energy density under double non-free interface constraint.

上述模拟结果分析,多孔CuAlMn 合金在不同界面约束下的变体自协调效应与马氏体形貌,与TEM 中观察到的实验结果符合较好.基于此,使用相场模型预测分析了其他类型的孔洞界面约束对马氏体相变的影响,包括引入不同尺寸的四重界面、方形界面,如图8 和图9 所示.图8 所示为四重界面约束下的变体自适应形貌结果,从图8(a),(b)中的模拟形貌中可以观察到,在单个非相变组织半径r=67.5 nm 的四重界面约束模拟中,观察到其变体在各个位置上厚度均匀,尺寸上与图3中(r=135 nm)单一界面约束下基本一致,为30 nm,相比局部界面约束与双重界面约束的结果厚度分布更加均匀.

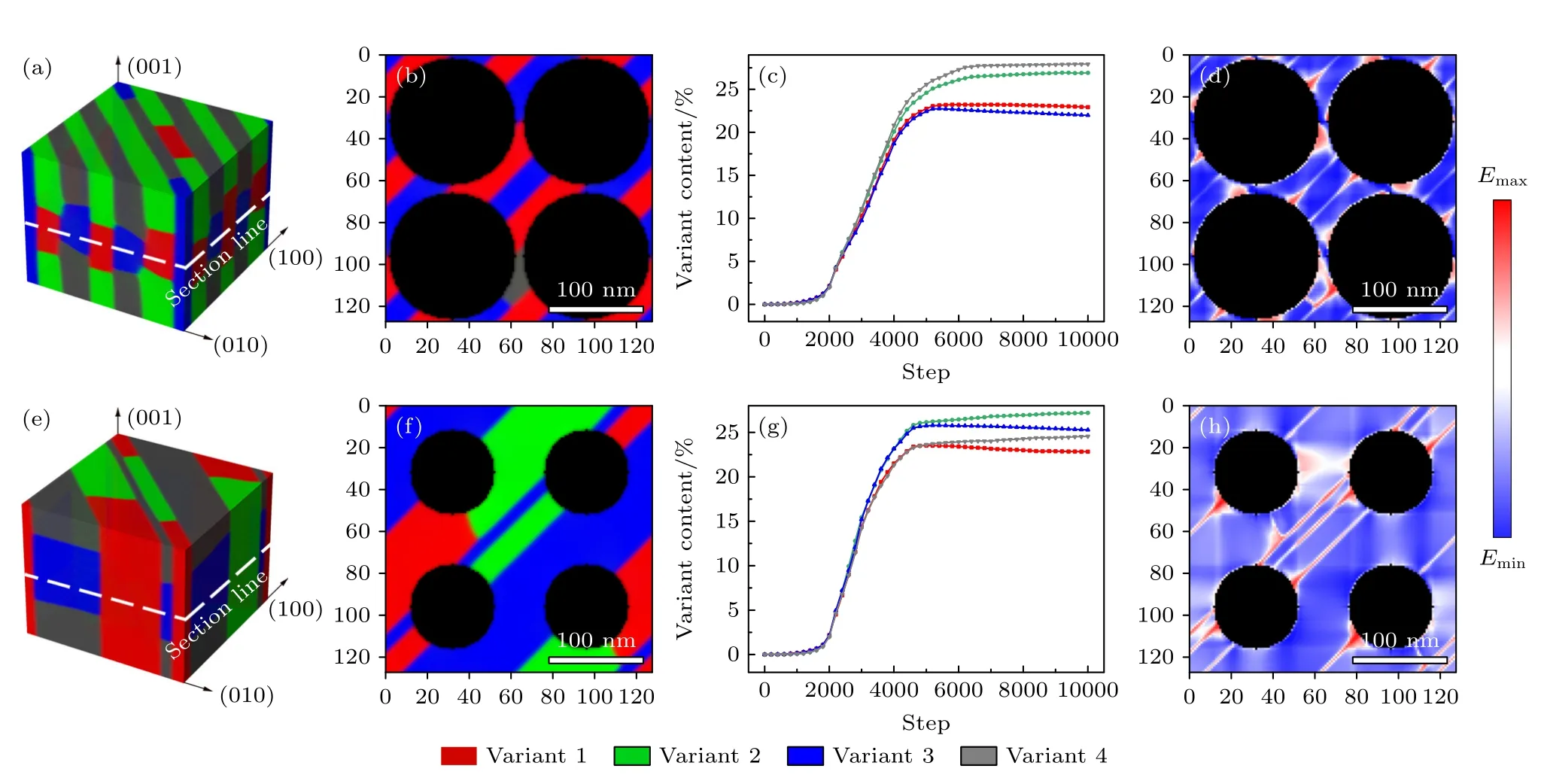
图8 CuAlMn 合金在四重非自由界面约束下的马氏体相变相场模拟结果,3D 模拟形貌,2D 切面形貌,各变体含量变化以及自由能分布示意图 (a)—(d)单个半径r=67.5 nm 的四重界面约束;(e)—(h)单个半径r=45 nm 的四重界面约束Fig.8.Phase-field simulations of the martensitic transformation of CuAlMn alloy under quadruple non-free interface constraint,3D simulation morphology,2D section morphology,variation of content of various variants and free energy distribution diagram:(a)—(d) Under the quadruple interface constraint of a single radius r=67.5 nm;(e)—(h) under the quadruple interface constraint of a single radius r=45 nm.

图9 CuAlMn 合金在方形非自由界面约束下的马氏体相变相场模拟,3D 模拟形貌,2D 切面形貌,各变体含量变化以及自由能分布示意图 (a)—(d)边长L=243 nm 的方形界面约束;(e)—(h)边长L= 198 nm 的方形界面约束Fig.9.Phase-field simulations of the martensitic transformation of CuAlMn alloy under square non-free interface constraint,3D simulation morphology,2D section morphology,variation of content of various variants and free energy distribution diagram:(a)—(d) Under the square interface constraint of a single side length L=243 nm;(e)—(h) under the square interface constraint of a single side length L=198 nm.

而在图8(e),(f)中,发现在r=45 nm 的小尺寸四重界面约束体系的模拟中,其变体厚度尺寸在空间分布并不均匀,整体形貌上与图5 中r=67.5 nm的局部界面约束下的模拟结果类似.从形貌角度分析,在非自由界面约束中,增大界面数目与增大非相变组织的半径对马氏体自适应结果的影响相似,都增大了界面影响区在样品中的比例,有助于变体条纹的细化作用.从图8(c),(g)中含量随步长的变化可以发现,界面的数量的增加同样会带来最终稳态下,变体含量间的差异性.通过图8(d),(h)的能量分析,发现在不同尺寸界面约束下,系统的能量分布均能保持在一个稳定水平,变体内部能量稳定,具有较高自由能的区域集中于变体间的边界.图9 展示两种不同尺寸的方形非自由界面约束,通过引入了不同边长的方形界面,模拟了稳态下的马氏体自适应形貌与各变体含量的变化情况.模拟结果与本文此前得到的结论相符,均可以观察到引入非自由界面后变体条纹的细化.相比尺寸小的方形界面,尺寸更大的方形界面的引入对变体条纹的细化作用更加明显,同时在含量变化上,其各变体含量的不均匀性也更加明显.结合以上模拟结果,可以认为在多孔材料中,通过增大多孔材料的比表面积,增大金属-空气非自由界面影响区域在样品中的比例,例如采用方形孔洞,更多的球形孔洞,可以使样品中马氏体组织变得更细小,马氏体变体之间的界面面积也会随之增大,从而具有更好的阻尼性能.

5 结论

1)基于与时间相关的金茨堡-朗道方程构建了不同界面约束下的相场模型.无界面约束、非自由界面约束、双重非自由界面约束中所模拟的结果均与实验观察到的形貌一致.实验及计算结果均表明,在金属-空气界面处的非相变组织的约束下,马氏体变体间的自协调形貌明显细化.

2)模型计算结果分析表明,引入非自由表面的尺寸、数量的增大,变体间含量的不均匀性也随之提高.结合自由能计算分析,组织细化虽一定程度增大了梯度能,但通过大幅降低整体应变能从而使系统总能量降低.

3)基于以上相场模型,研究了多孔材料中其他界面类型的约束下马氏体变体间自协调形貌的变化规律.结果表明,增大多孔形状记忆合金的比表面积,马氏体变体组织有变细小的趋势,从而进一步提升材料的阻尼性能.