用于星间激光干涉测量的分频相位计辅助弱光锁相*

乐陶然 穆衡霖 徐欣 谈宜东 尉昊赟 李岩

(清华大学精密仪器系,精密测试技术及仪器国家重点实验室,北京 100084)

弱光锁相是星间激光干涉测距的重要环节,通过锁相环跟踪外差干涉光信号相位.受散粒噪声、激光频率噪声等各类噪声限制,锁相环内部本地振荡器信号与外差信号间存在一定相位差,而锁相环的鉴相范围只有正负半个周期,若相位差某时刻超过鉴相范围,则本地振荡器在反馈调节下可能会进入错误的工作点,出现周跳,导致后续相位重构出错.本文提出了基于引力波探测背景的一种周跳诊断方法,在原锁相环基础上引入一个具有更大鉴相范围的辅助分频相位计,可以对锁相环是否出现周跳提供判断依据.结合已有的锁相环及噪声理论,建立了分频相位计的理论模型,以此数值模拟了分频相位计工作,模拟结果表明,分频相位计可以实现大范围鉴相,具有判断弱光锁相周跳的能力.

1 引言

星间激光干涉测量为现阶段空间引力波探测首选方案,天基引力波干涉仪用于探测低频段的引力波信号,干涉仪对应的工作基线可从几十万千米到几百万千米[1-5].激光干涉太空天线(LISA)是由欧洲航天局20 世纪80 年代提出,美国航天航空局共同参与的低频段引力波探测计划,中心敏感频段为0.1 mHz—1 Hz[6].LISA 使用3 个航天器组成三组星链,航天器距离在250 万千米左右,每个相邻航天器对之间有双向激光连接,每艘宇宙飞船上都有2 个测试质量,使得6 个宇宙飞船间连接形成3 个迈克耳孙干涉仪.LISA 通过测量迈克耳孙干涉仪两臂末端的惯性测试质量的位移来探测引力波[6].

在太空中,卫星间相对运动造成的多普勒频移可高达几MHz[7],因此LISA 等天基干涉仪采用外差干涉法测量航天器间位移[7,8].探测器得到的外差信号经模数转换器(ADC)数字化,在现场可编程门阵列(FPGA)中处理,通过锁相环[7,9]测量外差信号的相位,确定航天器间的位移.对于重力测量卫星 (GRACE-FO)和LISA 等天基干涉仪,锁相环需要实现长距离的相位跟踪,GRACE-FO 为几百千米[8],LISA 则是数百万千米[6].本地卫星发射的激光束经过长距离传输后,只有一小部分能被远端卫星的探测器接收到,以LISA 为例,其接收激光功率在100 pW[1].考虑到散粒噪声与本地光光强相关,即使通过较强的本地光来放大外差信号,信噪比也较低,加上如激光频率噪声、时钟抖动噪声等噪声的引入,误差相位抖动可能超出锁相环工作范围,因此需要对噪声传递过程给出全面的理论建模,估计误差相位大小[10].

Gerberding 等[11]提出了线性的星间干涉数字锁相环模型,验证其在较宽的频率范围内能高精度地测量外差信号相位.但是锁相环鉴相范围有限,较大的误差相位会使线性模型失效,即锁相环出现周跳,导致相位重构出错[12].Samuel 等[13]根据锁相环模型优化锁相环带宽,最小化由散粒噪声和激光相位噪声引起的误差相位标准差,实验设计的数字锁相环可以实现最低接收功率30 fW 的弱光锁相,周跳率小于0.01 s—1.Liang 等[14]从理论上分析了电子噪声、激光振幅噪声和散粒噪声对信噪比的影响,通过优化电路参数和光功率,提高了信噪比,实现了13 pW 光功率的低噪声锁相.并设计实验验证弱光锁相中主要的噪声来源[15].弱光锁相理论的发展不仅为技术本身提供依据,更对LISA和太极计划(TAJI)的时延干涉(TDI)仿真建模提供了依据[16].除了光路和电路上的改进,最近有学者提出通过结合光频梳采用特定的TDI 组合可以有效地降低弱光锁相噪声,简化后处理[17].虽然可以通过优化锁相环带宽等方法可以降低周跳发生概率,但仅凭单独的锁相环无法判断周跳是否发生.

本文在已有的锁相环模型基础上提出使用分频相位计辅助判断周跳的方法.将输入的外差信号转为方波信号N分频.并与锁相环缩小1/N的输出信号通过数字时间芯片(TDC)比较确定相位差.相较于一般的锁相环,分频相位计具有更大的鉴相范围,能够判断锁相环是否工作在错误锁定点.将弱光锁相模型与分频相位计原理结合,提出针对弱光锁相环节的分频相位计理论模型,并通过模拟验证理论模型正确性,结果说明分频相位计能在大范围内准确输出相位差,具有判断锁相环周跳的可行性.

本文在后续的弱光锁相环模型中总结了已有的锁相环及噪声模型,给出误差相位的表达式,并依次评估各类噪声的影响.提出分频相位计辅助的周跳诊断,给出辅助分频相位计工作原理及理论模型.并在实验模拟中给出基于分频相位计工作过程的时序模拟及结果.

2 弱光锁相环模型

2.1 星间锁相环原理

两个航天器间传输激光的相位随光程变化而变化.因此通过跟踪接收光场相位变化,就可以测量航天器间的位移.

图1 为干涉探测系统及锁相环的简化模型,主激光器输出的本地光和远端从激光器输出的信号光在探测器上干涉,探测到的电信号输入模拟前端电路、经ADC 转换成数字信号后进入基于FPGA的锁相环.

图1 星间激光干涉系统及锁相环Fig.1.Intersatellite laser interference system and phase-locked loop (PLL).

探测器探测信号可写为

其中PLO为本地光光功率,Psig为信号光光功率,fhet为外差频率,φhet(t) 为需要跟踪的外差相位.

本地振荡器为数控振荡器(NCO),其输出写为

其中fnco为NCO 输出频率,φnco(t) 为NCO 输出相位.

如图2 所示,使用混频器将两路信号相乘,经过低通滤波后得到

图2 锁相环构成Fig.2.Phase locked loop structure.

图3 线性锁相环模型框图Fig.3.Block diagram of the linearized PLL model.

Δf=fnco-fhet为NCO 与外差频率之差,εe(t)=φhet(t)-φnco(t)为NCO 和外差相位之差.在锁定状态下,NCO 频率认为等于外差频率,即 Δf为0,NCO 与外差信号相位差为小量.如果频率不相等,只要频率差在相位计[18]的拉入范围内,相位计仍然能够跟踪外差信号.在锁定状态下,滤波器输出

滤波器输出可近似正比于误差相位用来负反馈,通过比例积分(PI)控制器更新NCO 频率,使NCO 频率一直锁定在外差频率上.PI 控制器的输出以及预测的NCO 频率输入到相位增量寄存器(PIR)中作为频率驱动信号,频率驱动信号送入数控振荡器,在相位累加器(PA)中积分,得到NCO输出信号总相位,经查找表(LUT)输出正弦和余弦信号.正弦信号和余弦信号分别与探测器信号做乘法用于反馈更新及IQ 解调重构相位[19,20].

2.2 噪声模型

根据来源可将噪声分为干涉测量系统噪声和锁相环数字电路噪声.目前对弱光锁相涉及的各类噪声源已有全面的理论模型,本节对这些模型进行总结并评估噪声大小.

2.2.1 干涉测量系统噪声

干涉测量系统引入的噪声包括激光相位噪声、散粒噪声和光电探测器噪声.自由运转的Nd:YAG固体激光器相位噪声可写为[21]

由于量子涨落,光电探测器探测到光子数存在不确定度,即散粒噪声.可以计算出散粒噪声引起的相位噪声为[21]

其中P为参考光功率,对于LISA,接收光功率典型值为100pW[21],可以估计出散粒噪声约为6.9×10-6

光电检测系统引入加性噪声不仅有散粒噪声,还包括各种电学噪声.如暗电流、负载电阻的热噪声和1/f型噪声,这类噪声与光功率无关,可以通过优化电路来降低,而散粒噪声完全依赖于PD 接收到的光功率及其转换效率[22].在低参考光功率条件下,散粒噪声是主要的加性噪声源,因此后续只考虑散粒噪声产生的加性噪声.

2.2.2 锁相环内噪声

电子锁相环内产生噪声主要来源于各类量化噪声以及晶体振荡器的时间抖动.数字信号将连续信号截断为2 进制的N位,可以认为在原信号上叠加一个均匀分布白噪声,线性功率谱密度为[11]

其中,fsamp为采样率,ADC 将信号以有限位数采集相当于在原信号上添加了加性噪声,对于8 位,采样频率fsamp=40 MHz 的ADC,其引入的相位噪声为 0.56×10-6

相位读出误差是指NCO 中相位累加器的有限N位位数造成的读出误差.设相位累加器位数32 位,采样频率40 MHz,相位量化噪声为9×

NCO 输出相位的分辨率受到频率寄存器位数的限制,而频率的量化误差随时间的积分转化为相位误差.设采样频率40 MHz,寄存器位数32 位,相位读取误差产生的相位噪声为0.6×(1 Hz/f)×10-6

除了输出频率的分辨率受限外,NCO 内部超稳振荡器不能做到绝对稳定,其时间抖动造成的相位噪声称为时钟噪声,时钟噪声不仅与时间抖动大小有关,还和外差频率成正比.对于自由运转的晶体振荡器,其时间抖动噪声可估计为7×10-14·(1 Hz/f)在外差频率25 MHz的最坏情况下[21],时间抖动噪声为2.1×(1 Hz/f)×

外差频率25 MHz 时,各类噪声总结如表1 所示,散粒和激光相位噪声为主要贡献,因此后续只考虑散粒噪声和激光相位噪声对误差相位的影响.

表1 弱光锁相噪声总结Table 1. Noise of weak light phase locking.

2.3 锁相环噪声传递

不考虑回路延迟下,传递函数写为

其中k是控制器中比例路径的增益,m是积分路径的增益,一级积分项相对二级积分项变化较慢,因此增益带宽主要由一级积分项决定,增益带宽可近似表示为

为了保持良好的相位裕度,通过调节增益比将二级积分器占主导地位的频率保持在增益带宽频率的1/8[24].(8)式包含外差信号大小A,因此入射光功率的变化会影响传递函数大小及带宽[24].

根据2.2 节噪声分析及本节的锁相环模型,可以得到误差相位信号谱密度表达式:

(11)式中与散粒噪声相乘项为低通滤波函数,与激光相位噪声相乘项为高通滤波函数,说明控制器带宽越高低频激光相位噪声滤除得越多,而同时引入的散粒噪声越多.

图4 所示为相位误差的标准差作为相位计带宽的函数,计算不同接收光功率下(1 pW,10 pW和100 pW)自由运转激光和稳频激光两种光源的相位误差曲线.随着带宽的降低,不同接收功率的误差相位曲线收敛于激光相位噪声,而随着带宽的增大,曲线收敛于散粒噪声.由于稳频的激光光源相位噪声更低,其最小误差相位标准差比在相同功率下的自由运行激光要低,相位计更不容易失锁,且能够在更宽的带宽范围内保持低相位误差.

图4 误差相位标准差与带宽关系 (a)自由运转激光;(b)稳频激光Fig.4.Standard deviation of phase error as a function of bandwidth: (a) Free-running laser;(b) frequency-stabilized laser.

2.4 非线性与周跳

以上锁相环模型建立在线性近似的基础上,若误差相位εe超过大约1/4 周期后线性模型就会失效.

如图5 所示,误差相位大小超过1/4 周期后,(4)式低通滤波得到的 s in(εe) 不能再近似为εe,反馈信号不再随误差相位增大而增大.误差相位超过1/2 周期,反馈信号与误差相位不再同号,此时锁相环提供的反馈反而会让误差相位增大,远离正确的锁定点.当锁相环重新锁定时NCO 输出相位可能会与外差信号相位相差一个周期 2π,锁相环工作在错误的锁定点,这种现象称为周跳(cycle slip).周跳发生概率与误差相位大小有关,误差相位的增大会使周跳更容易发生,可将噪声视为高斯分布,某时刻误差相位超过0.5 cycles 时发生周跳,当误差相位标准差为0.1 cycles,周跳概率约为5×10-7,当标准差为0.2 cycles,则周跳概率约为0.01[24].

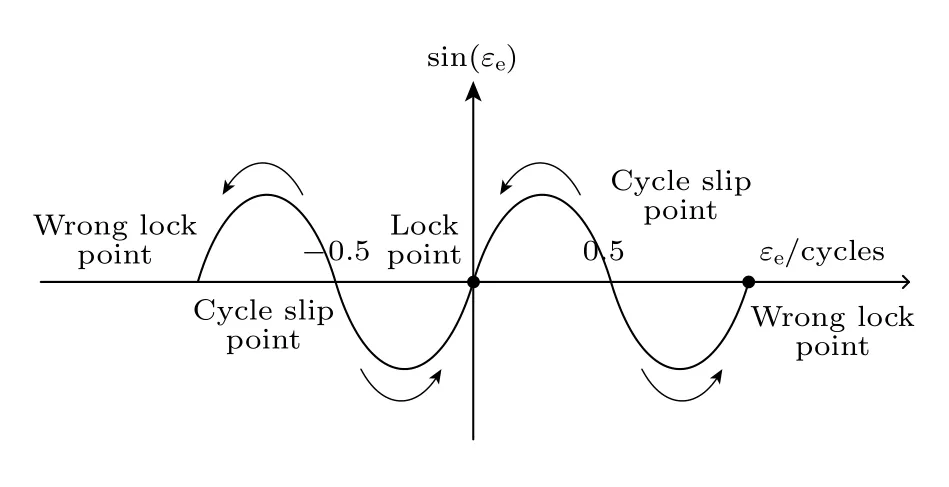
图5 锁相环中的周跳Fig.5.Cycle slipping in a phase locked loop.

对于星间激光干涉测量任务,周跳会使重构得到的相位出现整周期偏差.除了降低误差相位减小周跳的概率外,可以引入辅助相位计判断周跳是否发生,为相位重构提供修正依据.

3 分频相位计辅助的周跳诊断

为了实现周跳诊断,可以在原有的锁相环基础上添加一个鉴相范围更大的辅助相位计,将信号分频扩大相位差判断范围.数字信号电子分频可以使用计数器或锁相环实现,如图6 所示,通过计算两路方波信号上升沿时间差确定相位差,数字相位测量不受非线性影响,因此鉴相范围可以达到半个周期,经过电子分频后可以进一步扩大鉴频范围.经过N分频后,数字信号的相位噪声幅度变成原来的1/N,同样采样抖动或是量化误差带来的相位噪声分频后也会缩小到原来的1/N,因此总相位噪声为原来的1/N.与方波信号不同,普通的模拟信号分频技术如米勒分频器[25]引入的相位噪声较大,不适用于高精度的相位计,因此模拟信号要实现分频,可以先转成同频同相的方波信号.图7 所示为分频相位计的原理图,光电探测器信号经过带通滤波后提高信噪比,使用迟滞比较器将正弦信号转换为同频的方波信号,由于门限电压及传输延迟,比较器输出信号相对输入的正弦信号有时间延迟,将比较器输出分频得到时间数字芯片TDC 的一路输入.辅助相位计中的本地振荡器根据PIR 读出端口得到缩小1/N倍的频率驱动信号,输出与原锁相环同频同相的方波信号作为TDC 第2 路输入.计算得到两路方波的上升沿时间差,确定误差相位大小,商用时间数字芯片如TDC-GP22 双通道模式时间分辨率约为45 ps,对20 MHz 的外差信号,相位分辨率约为0.007 rad,满足诊断需求.

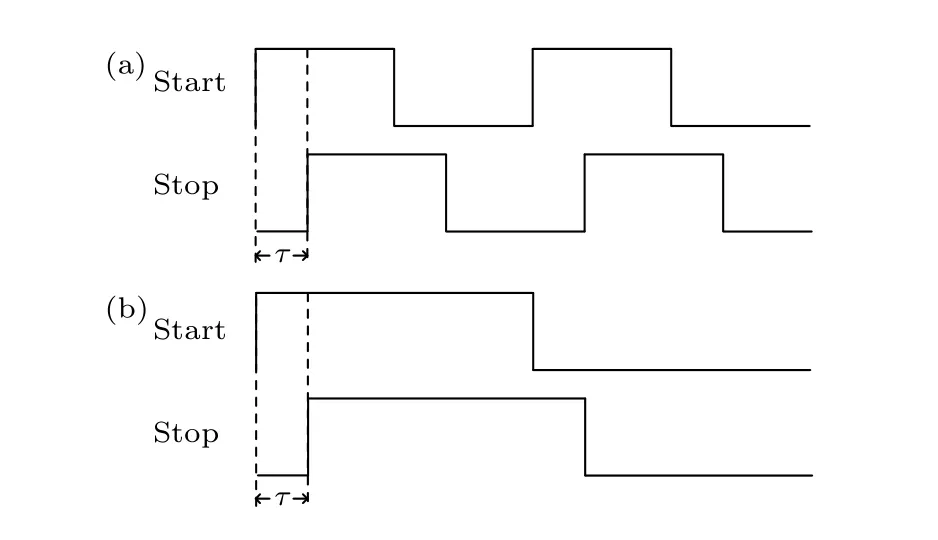
图6 (a)方波信号相位差测量;(b)分频后的方波信号Fig.6.(a) Square wave signal phase difference measurement;(b) square wave signal after frequency division.

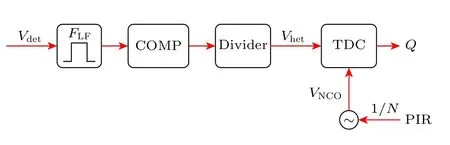
图7 分频相位计模型Fig.7.Frequency division phase meter model.

光电探测器输入信号可写为

其中A为信号幅度,φlaser为激光相位噪声为散粒噪声.使用一个带宽1 MHz 的FIR 带通滤波器,其中心频率由锁相环内NCO 频率决定.可以计算经过滤波器后散粒噪声标准差为(Psig=100 pW,Fug=1 MHz)

而在一个拍频信号周期内自由运转激光相位噪声标准差:

σφshot≪1表明滤波后信号信噪较好,散粒噪声大小远小于信号幅值,σlaser≪1 表明在一个拍频周期内相位噪声几乎不改变正弦波形状.若正弦信号淹没在噪声中,或者一个周期内正弦信号严重变形,比较器无法准确地将正弦信号转为方波.

由于散粒噪声的存在,输入信号在门限值附近有微小抖动,可以设置合适的迟滞比较器上下门限电压ug,确保散粒噪声基底不会造成输出电压的抖动.比较器输出方波可以写为

将方波信号输入除法器,分频得到一路TDC输入信号:

τdivider为比较器传输延迟,以商用比较器SY89230 UMG 为例,其传播延迟最大0.85 ns,抖动标准差为1 ps,外差频率25 MHz 情况下对应相位延迟约为0.134 rad,相对于整周期可以忽略,因此后续不考虑该项.锁相环频率寄存器输出为NCO 信号频率,从PIR 读取口分出一路并将值缩小1/N后输入到分频相位计的NCO 中,输出与锁相环内NCO同频同相的方波信号,写为

其中t1和t2分别为两路信号测量到上升沿时各自的时间,考虑到φCOMP和φNCO两路信号受带宽限制没有高频分量,可以认为φhet(t2)≈φhet(t1) .(18)式可写为

其中φhet(t)-φNCO(t) 可以写为 Δφ(t) .

观察到测量的上升沿时间差不受信号分频的影响,若不进行分频,当时间差τ超过半个周期时,辅助相位计就无法判断相位差;使用N分频后,相位计鉴相范围扩大N倍,辅助相位计能在时间差τ超过半个周期情况下鉴相.将(16)式和 (17)式代入(19)式,得到相位差频谱:

(20)式与图3 中Q点输出频谱相同,即分频相位计和原锁相环都有鉴相的作用.根据(11)式,锁相环误差相位为

由于散粒噪声直接影响了鉴相,分频相位计得到的相位差与锁相环误差相位有一定偏差,这与原锁相环结果相同[11].若锁相环工作在激光相位噪声主导频段,则(20)式和(21)式可改写为

此时分频相位计输出可以直接反映误差相位大小.下文将构造噪声时间序列模拟相位计的工作,说明分频相位计判断周跳的可行性,并验证分频相位计输出在一定情况下可以直接反映误差相位的大小.

4 实验模拟

4.1 噪声时间序列

设外差频率25 MHz,TDC 内部频率1 GHz,分频相位计做10 分频.模拟在时间域上进行,已知激光相位噪声、散粒噪声及各类噪声的谱密度,为了恢复噪声在时域的随机性,可以为各类噪声分别生成一组随机的相位谱,噪声谱密度和相位谱构成了完整的噪声信息,通过傅里叶变换即可得到噪声的时间序列.

图8(a),(b)分别为构造的激光相位噪声和散粒噪声序列谱密度及二者谱密度的理论值,构造的相位噪声和散粒噪声密度与理论值符合得较好,说明生成的时域序列可以较好地表示对应的噪声.

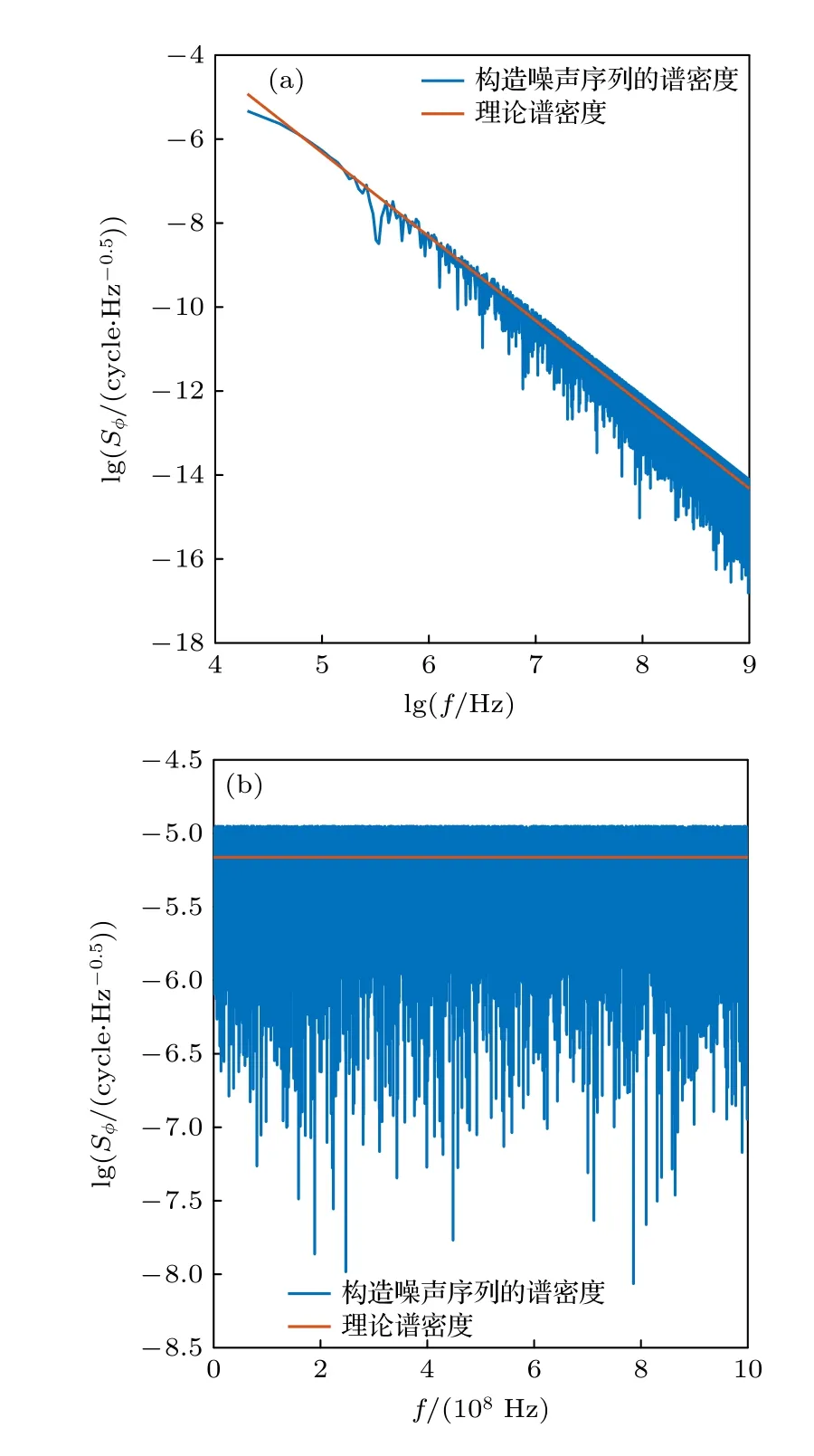
图8 (a)构造的激光相位噪声谱密度与谱密度理论值;(b) 构造的散粒噪声谱密度与谱密度理论值Fig.8.(a) The constructed spectral density and theoretical value of spectral density of laser phase noise;(b) the constructed spectral density and theoretical value of spectral density of granular noise.

4.2 模拟相位计工作

在生成激光相位噪声及散粒噪声后,按(12)式构造外差信号序列,设A=1 V,在此情况下φshot×1 V[11].设计一阶巴特沃斯滤波器作为带通滤波,中心频率25 MHz,带宽1 MHz,得到滤波后信号如图9(a)所示,信号有较高的信噪比.通过模拟迟滞比较器将正弦信号转为方波,设置上下门限电压为0.05 V,对应相位误差约为0.05 rad,考虑到散粒噪声引入的加性噪声标准差约为0.0069 V,0.1 V 的门限电压可以较好地消除散粒噪声基底可能引起的抖动.得到方波序列后,用类似D 触发器分频的原理对信号做分频,结果如图9(b)所示.

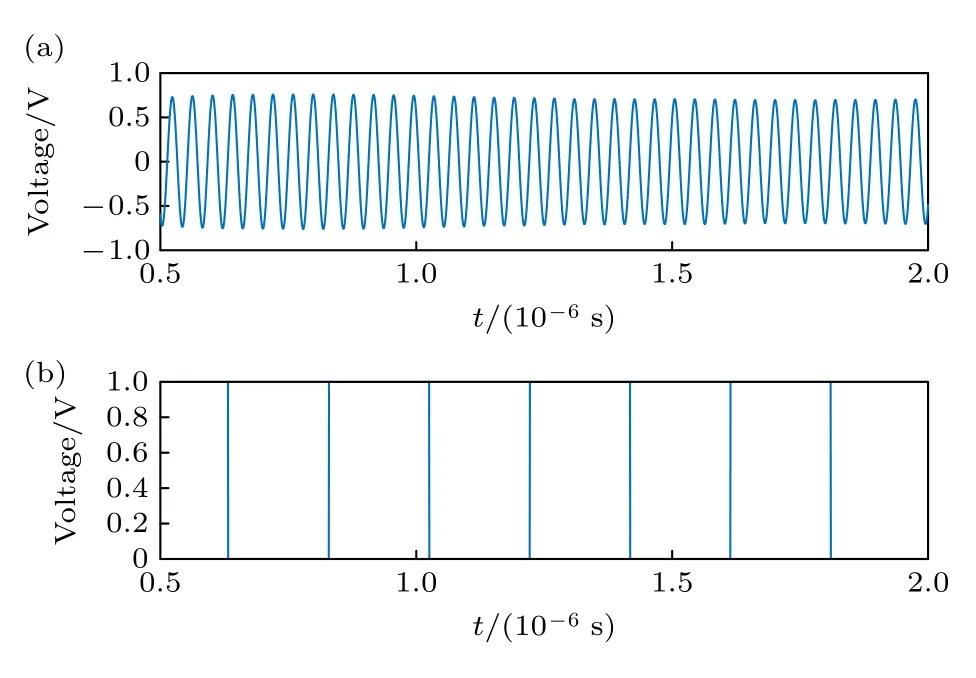
图9 (a)滤波后得到的正弦信号序列;(b)将正弦信号转方波并经过10 分频后的结果Fig.9.(a) The sinusoidal signal sequence obtained after filtering;(b) converting sinusoidal signal into square wave and passing through 10 frequency division.

辅助相位计NCO 相位时间序列由φNCO(f) 傅里叶变换得到,φNCO(f) 中的激光相位噪声和散粒噪声为图8 中的数据.两路方波信号作为输入计算上升沿时间差,最终相位计得到两路信号相位差Δφ(f),由(19)式知相位分辨率为

以外差信号频率25 MHz,采样率频率1 GHz 为例,相位分辨率 Δφmin≈0.079 rad .实际的TDC 相位分辨率会更高.

4.3 实验结果

首先使用两路相位差从-10π 递增到 1 0π 的正弦波时间序列作为预设的外差信号和PIR 端口信号,经过模拟得到相位计输出相位差,如图10 所示.考虑到TDC 测量时间的单向性,当相位差为负时,相位计输出与相位差相差整周期,图中预设相位差从-10π 到0 时,分频相位计输出从 1 0π 到20π,预设相位差从0 到 1 0π 时,分频相位计输出同步,表明分频相位计能在鉴相范围内正确地输出两路相位差.

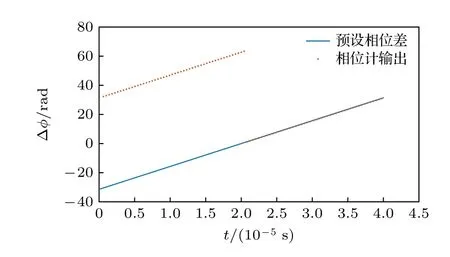
图10 分频相位计输出正确地表示相位差Fig.10.The output of frequency divider phase meter correctly represents the phase difference.

为了验证系统具有判断相位周跳的能力.在生成的φNCO时间序列上减少和增加一系列整周期模拟锁相环周跳.根据分频相位计的理论分析知,锁相环工作在错误的锁相点不改变相位噪声谱密度,但 NCO 输出和外差信号相位相差整数周期,超出了锁相环鉴相范围.设分频相位计做10 分频,锁相环带宽为1 kHz,得到分频相位计输出如图11所示,在图11(a),(c),(e)中,NCO 信号分别减小 2π,4π和6π 相位,对应的相位计输出 Δφ(t) 表明外差信号比锁相环NCO 信号相位增大 2π ,4π和6π .在图11(b),(d),(f)中,NCO 信号分别增大 2π ,4π 和6π 相位,对应的相位计输出 Δφ(t) 表明外差信号比锁相环NCO 信号相位减小 2π ,4π和6π .因此分频相位计可以判断锁相环是否工作在正确的锁定点,而其他鉴相方法如IQ 解调方法不能做到.

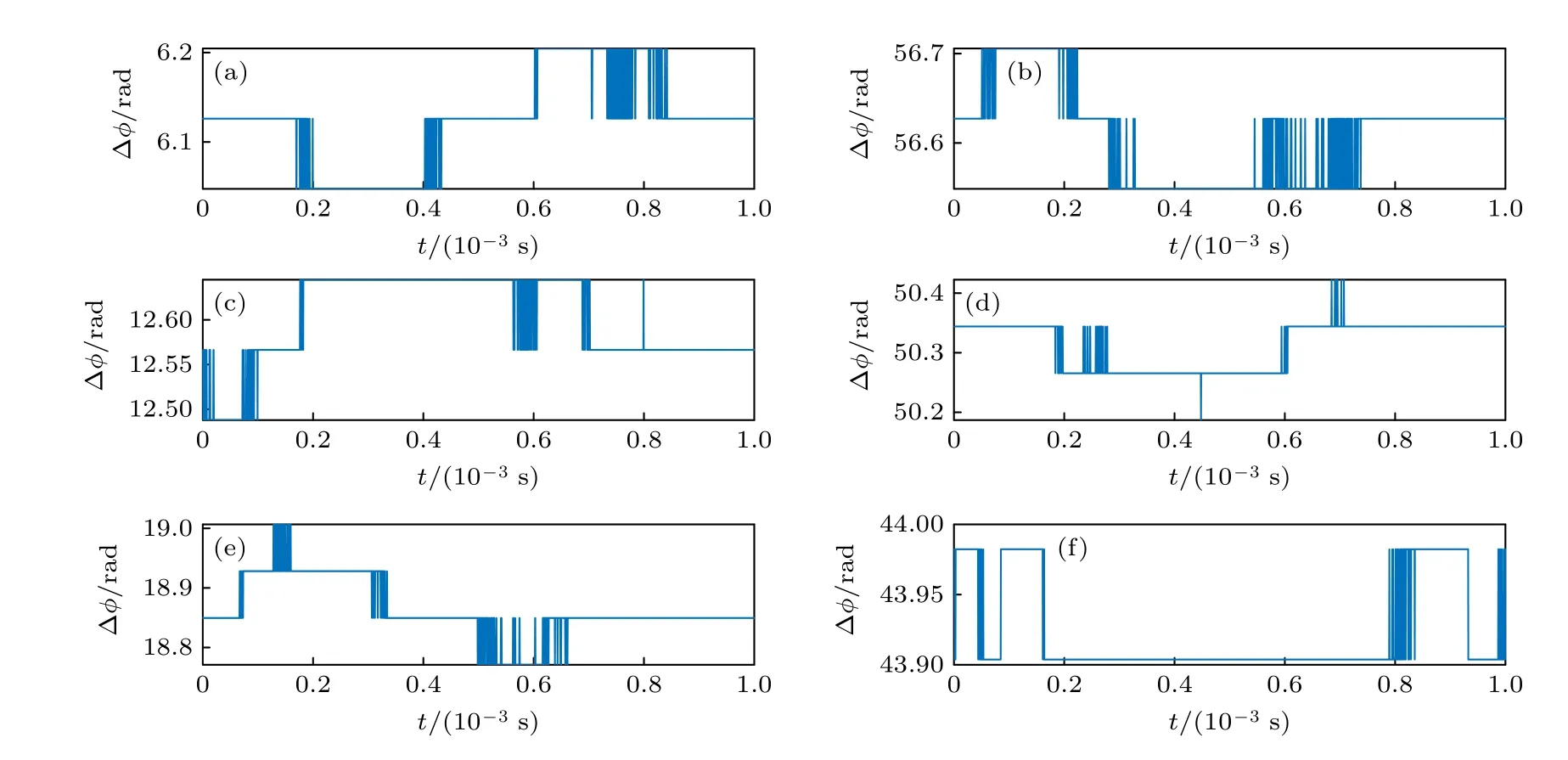
图11 (a),(b) NCO 相位减小或增大 2 π 分频相位计的输出;(c),(d) NCO 相位减小或增大 4 π 分频相位计的输出;(e),(f) NCO相位减小或增大 6 π 分频相位计的输出Fig.11.(a),(b) NCO phase decreases or increases by one period,the output of the frequency divider phase meter;(c),(d) NCO phase decreases or increases for two periods,the output of the divider phase meter;(e),(f) NCO phase decreases or increases for three periods,the output of the divider phase meter.

为了验证分频相位计输出与误差相位的关系,图12 所示为锁相环带宽100 Hz 下一段时间内误差相位以及分频相位计输出的时间序列,考虑到相位差小于0 时图像不直观,这里相位差添加了一个偏置 π .图12 所示为分频相位计输出和误差相位相当,两者存在一定偏差,为门限电压引起的相位误差,因此在激光相位噪声主导的频段内,分频相位计输出可以直接反映误差相位的大小,这与(22)式,(23) 式给出的结论相同.

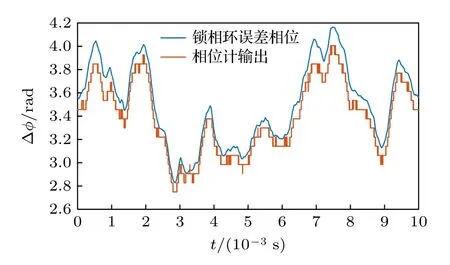
图12 一段时间内的误差相位和分频相位计输出Fig.12.Error phase and frequency division phase meter output over a period of time.

以上模拟结果说明基于星间激光干涉的分频相位计具有大范围鉴相的特点.当相位差变化超出一般相位计鉴相范围时,分频相位计可以正确输出而不发生周跳.分频相位计与一般相位计输出相同,在激光相位噪声主导的情况下,相位计输出可以直接反映误差相位,并通过数值模拟直观地验证了这一点.

5 结论

本文建立了数字弱光锁相环模型,评估了各类噪声的影响.根据最主要的两种噪声(激光相位噪声及散粒噪声)给出了误差相位的理论谱密度.考虑到锁相环的鉴相范围有限,较大的误差相位或会导致周跳,使锁相环工作在错误的锁定点.本文提出分频相位计解决鉴相范围较小的问题,首先将输入的外差正弦信号转为同相方波进行数字分频后作为TDC 一路输入,再将锁相环提供的累计相位除以N,输出同相方波信号作为TDC 另一路输入,通过TDC 计算上升沿时间差获得两路信号相位差.模拟结果表明该分频相位计的输出能正确反映两路原始信号的相位差,由于分频相位计具体更大的鉴相范围,其输出可以判断锁相环是否工作在正确的锁相点,并在一定条件下直接反映误差相位大小,验证了分频相位计模型,说明使用分频相位计用于判断周跳具有一定可行性.本文提出的辅助分频相位计可以运用在以 LISA 为代表的弱光锁相任务中,对锁相环的工作状态做出诊断.未来将开展进一步实验探究各类参数对相位计性能的影响.例如根据分频相位计理论,N分频的N越大鉴相范围越大,随之带来的是周跳反应时间的延长,实际情况可能需要权衡这两方面.目前的理论只考虑了分频相位计对弱光锁相任务的作用,未来可以结合锁臂和时延干涉技术分析分频相位计对整个探测系统的贡献.