双链超导量子电路中的拓扑非平庸节点*

关欣 陈刚

1) (太原学院材料与化学工程系,太原 030032)

2) (山西大学激光光谱研究所,量子光学与光量子器件国家重点实验室,太原 030006)

3) (山西大学极端光学协同创新中心,太原 030006)

4) (郑州大学物理学院,郑州 450001)

拓扑无能隙系统作为不同量子相的连接,目前已经成为备受关注的前沿科学.超导量子电路作为一个重要的全固态量子器件是宏观调控量子效应的优秀平台.本文在超导量子电路中构建了双链的Su-Schrieffer-Heeger(SSH)模型并发现了拓扑非平庸的节点.首先设计了电容耦合的双链transmon 比特,之后用两个交流微波驱动每一个transmon 比特,从而实现比特间耦合强度的独立调控,最后通过选择比特间合适的耦合参数实现交错的双链SSH 模型.接下来探索了交错双链SSH 模型的拓扑性质,首先计算了k 空间中双链SSH 模型的本征能量,并发现了两种类型的相边界.之后在参数空间中画出了拓扑相图,发现了两类拓扑绝缘相,其拓扑数分别为1 和—1,对应有两类边界态.拓扑相图也进一步给出了两类相边界的分布以及它们两侧拓扑数的值.最后分析了两类相边界的拓扑性质,发现其中一类拓扑相边界对应的能带有两个拓扑非平庸的节点.本文的工作为探索链条型物理系统、拓扑物态以及节点型拓扑半金属提供了新的途径.

1 引言

近年来,微纳米技术的快速发展使得全固态量子器件超导量子电路成为了量子信息[19-22]、量子计算[23-26]以及量子模拟[27-34]的优秀平台.相比于其他量子平台,超导量子电路系统在扩展性、集成性、调控性等方面都具有更大的优势[35-38].基于这些优势,大量的量子模拟工作已经在超导量子电路系统中实现,如多体局域化[28]、动力学量子相变[27]、磁性物理[29,30]、量子行走[39]以及拓扑材料[31,32]等.最近,实验[40]上已经实现了由24 个最近邻耦合的transmon 比特构造的双链结构,并模拟出了双链玻色-哈伯德模型,进一步探索了系统中单激发和双激发的动力学特性.同时,实验[41,42]中实现了transmon 比特之间耦合强度的独立可调,并且模拟出了单链的Su-Schrieffer-Heeger (SSH)模型,进一步观测到了拓扑非平庸的磁子绝缘体[31].因此,基于目前的实验现状,可以通过改变双链transmon 比特间的耦合强度在超导量子电路中实现双链SSH 模型.

基于以上的实验及理论工作,本文提出了利用transmon 比特实现耦合强度独立可调的双链SSH 模型的可行性实验方案,并在这一模型中发现了拓扑非平庸的节点.本文首先设计了电容耦合的双链transmon 比特,然后用两个交流微波驱动每一个transmon 比特,从而实现比特间耦合强度的独立调控,最后通过改变比特间耦合参数实现交错耦合的双链SSH 模型.接下来探索双链SSH 模型的拓扑性质,首先计算k空间中双链SSH 模型的本征能量,并发现了两种类型的相边界.之后在参数空间中画出拓扑相图,发现了两类拓扑绝缘相,拓扑数分别为1 和—1,对应有两类边界态.拓扑相图也进一步给出了两类相边界的分布以及它们两侧拓扑数的值.最后分析了两类相边界的拓扑性质,将布洛赫态映射为k空间的矢量场,发现第一类相边界对应能带的节点处,矢量场存在两个扭结.两个节点有相反的拓扑荷分别为1 和—1,并且受到平移和反转对称性的保护.另外,本文发现第二类相边界的能带节点是拓扑平庸的.本文的工作为探索链条型物理系统、拓扑物态以及节点型拓扑半金属提供了新的途径.

2 理论模型

目前,双链耦合的超导量子比特链已经在实验上实现[40].基于这一实验,本文用transmon 比特设计了双链的Su-Schrieffer-Heeger (SSH)模型.如图1(a)所示,两条比特链中所有最近邻比特之间都通过电容进行耦合,相应的拉氏量表示为

图1 双链SSH 模型 (a) 两条transmon 比特链分别标记为A 和B.每个transmon 比特都与其最近邻比特两两耦合.这里所有的耦合器均为电容. Q νj 表示的是第ν 条链上的第j 个比特. C νj 和分别是第ν 条链上,第j 个比特的有效电容和约瑟夫森能.Cνij 是耦合第ν 条链上,第i 和第j 个比特的电容. C ABj 表示A,B 两条链上第j 个比特之间耦合的电容. φ νj 是第ν 条链上,第j 个比特的约瑟夫森结的相位.本文中transmon 比特的约瑟夫森结由超导量子干涉仪(SQUID)形成,是SQUID 中每个约瑟夫森结的能量.每个比特都受到两个外加磁通的调制.(b) 双链SSH 模型示意图,图中红色和蓝色的实心球表示SSH 模型中一个原胞的两种比特Fig.1.Two-leg SSH model: (a) Two-leg (labeled respectively by A and B) superconducting circuits with transmon qubits.The qubits are coupled with their nearest-neighbor sites.All couplers are capacitors. C νj andare the effective capacitance and the Josephson energy of the qubit at the jth site on the ν th leg. C νij and C ABj are the capacitors to couple the qubits at the jth site on the ν th leg with its nearest-neighbor sites along each leg and between the legs,respectively. φ νj is the phase of the Josephson junction of the qubit at the jth site on the ν th leg.The Josephson junction of the transmon qubit is a superconducting quantum interference device(SQUID).is the Josephson energy of SQUID.Each qubit is modulate by two external magnetic fluxesand

式中,每条链上比特的位置用j标记,不同的链用ν=A/B来标记.第ν条链上,第j个比特的电容用Cνj来表示.第ν条链上,第j个比特的约瑟夫森能用表示.第ν条链上,第i和第j个比特之间耦合的电容用Cνij表示.A,B两条链上第j个比特之间耦合的电容用CABj表示.第ν条链上,第j个比特中约瑟夫森结的相位用φνj表示,φ0=1/(2e)是其量子化单位.〈i,j〉是每条链上最近邻比特的求和.如果选择为正则坐标,相应的正则动量可以表示为

为了实现双链SSH 模型,需要调节比特间的耦合强度,本文利用两个交流微波对每个transmon比特进行驱动.实验上可以通过磁通偏置线实现这种驱动[41,42].如图1(a)所示,将transmon 比特的约瑟夫森结替换成超导量子干涉仪(SQUID).将两个独立可控的交流磁通设置在SQUID 的回路中

3 拓扑相图

式中ε(k)=(εx,εy,εz) ,其中εx=(t1+t2)cos(k)+1,εy=(t1-t2)sin(k),εz=0 .是三维泡利算符.k空间中的能谱可以通过对角化哈密顿量(28)式得到:

讨论 SPT多好发于30岁左右的年轻女性[4]。Papavramidis等[5]的一组大数据中97.8%的患者为女性，平均年龄为22岁。Yu等[6]报道中国人SPT患者男女比例为1∶8.37，平均年龄27岁，本组患者女性占85.19%，平均年龄为30岁，与文献报道结果相符。

由(29)式可知,能谱的两个能带会在ε±=0时发生简并.当ε±=0 时有:

其中kc是能带简并点的波矢.通常情况下,参数空间中能带简并点两侧的拓扑性质会发生变化.由(30)式和(31)式可知,根据kc的不同取值,拓扑相边界可以分为两类.第一类是当kc/=0 时,有t1=t2以 及 c os(kc)=-1/(2t2) .第二类是当kc=0 时,即 s in(kc)=0 时,有 c os(kc)=-1/(t1+t2) .那么,可以得到第一类相边界:

第一类相边界的能带有两个节点±kc.第二类相边界的能带有一个节点kc=π 或kc=0 .两类相边界有两个交点,为t1=t2=±1/2 .本文将两类相边界以及交点t1=t2=±1/2 上对应的能带图画在了图2中,可以更直观地看到第一类相边界对应能带的两个节点(图2(a))以及第二类相边界对应能带的一个节点(图2(b)).另外,第一类相边界能带的两个节点在相边界交点处相遇,变为一个节点(图2(c)).

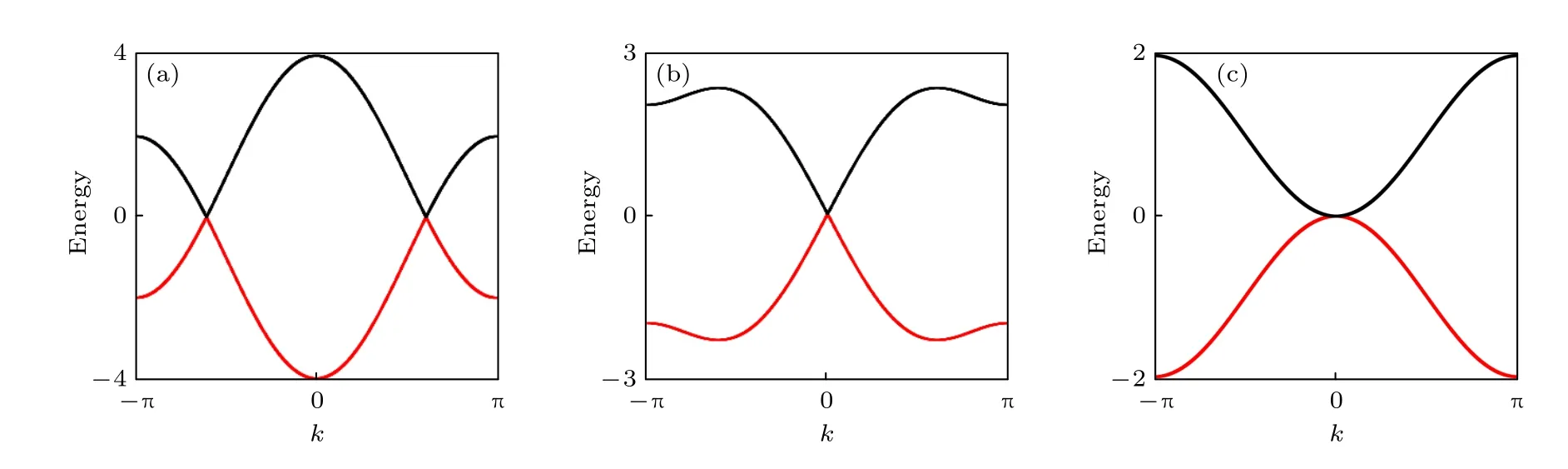
图2 双 链SSH 模型的能谱图 (a) t1=t2=1.5 ;(b) t1=-1.5 和t2=0.5 ;(c)t1=t2=-0.5Fig.2.Energy bands of SSH model: (a) t1=t2=1.5 ;(b) t1=-1.5 and t2=0.5 ;(c) t1=t2=-0.5 .

接下来,进一步探索相边界两侧的拓扑性质.首先需要计算拓扑不变量.本文中,由于哈密顿量有PT 对称性,因此根据Altland-Zirnbauer拓扑分类[44],能带的拓扑不变量为绕数:

根据拓扑不变量N的分布,图3 给出了参数空间中的相图.图中红色实线标记的是第一类相边界((32)式),发现相边界两侧的拓扑不变量分别为—1 和1.这表明第一类相边界的两侧区域中,能带都是拓扑非平庸的,并且两侧区域的拓扑不变量之差为2.黑色实线标记的是第二类相边界((33)式),边界两侧的拓扑不变量分别为0 和1 或0 和—1.这表明第二类相边界两侧中总有一侧是拓扑平庸的,另一侧是拓扑非平庸的,并且两侧区域的拓扑不变量之差为1.

图3 双 链SSH 模型在参数空间 t1-t2 中的拓扑相图.深绿色的区域是拓扑数 N =-1 的区域,浅咖色的区域是拓扑数 N =1 的区域,浅绿色的区域是拓扑数 N =0 的区域;红色的线标记的是第一类相边界,黑色的线标记的是第二类相边界Fig.3.Topological phase diagram in the t1-t2 plane.The bottle green,light coffee color and pale green areas indicate the areas with N =-1,N =1 and N =0 respectively.N denotes the winding number.The red and black lines indicate the first and second phase boundaries respectively.

接下来进一步讨论开边界条件下相图中不同区域的特性.根据体边对应原理[45,46],当体态表现为拓扑非平庸时,边界态是没有能隙的.因此,图3中的拓扑非平庸区域在开边界条件下其能带会出现准0 能模.为了证明这点,图4 给出出了开边界条件下的能带图以及相应的波函数.图4(a1)是N=1时对应的能带,可以看出,在能量0 点处出现了两个简并的能隙闭合点.相应的波函数ψα(j)画在图4(b1)中,可以看出其呈指数地局域在系统的边界上,这正是拓扑相在开边界条件下的一个显著特征.图4(a2)和图4(b2)是N=-1 时对应的能带及波函数,它们与图4(a1)和图4(b1)有相同的特征.图4(a3)和图4(b3)是N=0,也就是拓扑平庸时对应的能带及波函数,可以发现此时0 能简并消失,出现能隙,并且波函数没有边界局域的特征.

图4 开边界能带和边界态 (a1) t1=1.5 和 t2=0.5 ;(a2) t1=0.5 和 t2=1.5 ;(a3) t1=0.5 和 t2=0.3 .(b1 )—(b3 )是(a1)—(a3)中第20 个能带的波函数Fig.4.Energy bands with open boundary condition with (a1 ) t1=1.5 and t2=0.5 ;(a2 ) t1=0.5 and t2=1.5 ;(a3 )t1=0.5 and t2=0.3 .The wave functions corresponding with the 20th energy bands of (a1 ),(a2 ),and (a3 ) are plotted in (b1 ),(b2),and (b3),respectively.

4 节点的拓扑特性

由上文知,系统存在两种类型的相边界.可以发现,这两类相边界最显著的不同是,第一类相边界两侧的相区域都是拓扑非平庸的且拓扑数相差2;第二类相边界两侧的相区域总有一侧是拓扑平庸的,另一侧拓扑非平庸且两侧拓扑数相差1.那么这两类相边界是否有不同的拓扑性质呢? 本节将讨论这个问题.

由哈密顿量(29)知,ε在布洛赫球的x-y平面上的轨迹为一个正椭圆:

对于第3 节中拓扑数为1 和—1 的相区域,该椭圆运动轨迹的旋转方向相反但均将原点 (0,0) 包含在椭圆内部(图5(a)和图5(b)).而对于拓扑数为0 的相区域,该椭圆始终没有将原点 (0,0) 包含在椭圆内部(图5(c)).布洛赫球上的原点正是上文中得到的能级简并点.这与第3 节得到的结论是一致的.那么,当参数取在相边界上时,椭圆轨迹会有怎样的变化呢? 对于第一类相边界,参数满足(30)式,椭圆轨迹方程(35)变为布洛赫球x轴上的线段(图5(d)):

图5 不同参数下 ε 在布洛赫球的 x -y 平面上的轨迹 (a)拓扑数 N =1 时 ε 的轨迹,参数设定为 t1=1.5 和 t2=0.5 ;(b)拓扑数 N =-1 时 ε 的轨迹,参数设定为 t1=0.5和t2=1.5 ;(c)拓扑数 N =0 时 ε 的轨迹,参数设定为 t1=1 和t2=-0.7 ;(d)参数满足第一类相边界 t1=t2 时 ε 的轨迹,参数设定为 t1=t2=1 ;(e)参数满足第二类相边界t1+t2=1 时 ε 的轨迹,参数设定为t1=0.8 和 t2=0.2 ;(f)参数满足第二类相边界 t1+t2=-1 时 ε 的轨 迹,参 数设定为 t1=-1.3和t2=0.3 .图中红点表示原点,箭头表示轨迹的运动方向Fig.5.The curve of the vector ε in x -y plane of the Bloch sphere with (a) t1=1.5 and t2=0.5 ;(b) t1=0.5 and t2=1.5 ;(c) t1=1 and t2=-0.7 ;(d) t1=t2=1 ;(e) t1=0.8 and t2=0.2 ;(f) t1=-1.3 and t2=0.3 .The red points and arrows indicate the origin points and direction of the curve respectively.

显然,这是一个以 (1,0) 为平衡位置,4|t1|为振幅的简谐振动.对于第二类相边界,参数满足(31)式,椭圆轨迹(35)式仍为一个正椭圆(图5(e),(f)):

该椭圆的半轴长度分别为1和|2t1±1|,并且可以注意到,该椭圆会经过原点 (0,0) .至此可以看到,ε在这两类相边界上有完全不同的运动轨迹.最重要的是,轨迹方程(36)在完成一个振动周期后会经过两次原点 (0,0),并且两次运动轨迹的方向相反,而轨迹方程(37)在完成一个运动周期后只经过了一次原点 (0,0) .从这里可以看出第一类相边界上的能带是拓扑非平庸的,而第二类相边界上的能带是拓扑平庸的.

接下来,分析拓扑相边界的另一些拓扑特性.首先,在k空间定义一个三维的矢量场F(k) :

其中sgn(·)是符号函数.可以看出,场F存在扭结,扭结出现在kc=arccos(-1/2t1) 的位置,在第一布里渊区 (-π,π] 中,kc有两个取值.这两个扭结正是第一类相边界的能带简并点.两个扭结的拓扑荷分别为1 和—1.为了直观地看到场F的扭结,图6 给出了(40)式中自旋期待值随k的变化.从这里也能够判断出,第一类相边界上的两个能带简并点(也称为节点)是受到拓扑保护的.

图6 参数设定为 t1=t2=1 (第一类相边界上)时矢量F(k) 随波矢k 的变化.图中箭头表示自旋的方向,kc 为能级简并点处的波矢Fig.6.The variation of the vector F (k) as k changes with t1=t2=1 .The arrows and kc indicate the direction of the spin and degenerate energy point respectively.

对于第二类相边界,即参数满足|t1+t2|=1时,场矢量F(k) 为

此时场矢量F与k无关,也就是说这时不存在扭结.因此,这时的节点是拓扑平庸的.

至此,了解到只有第一类相边界的能带节点是受到拓扑保护的,因此在这一节点处一定有其独有的对称性.接下来讨论这一问题.当系统处在第一类相边界时,参数满足t1=t2.这时系统不再是双链SSH 模型,而变成了两条完全相同的比特链.这时会出现两个双链SSH 模型中没有的对称性.这两个对称性分别用一步平移算符和子格子反演算符来刻画.这两个算符的作用分别为

由上文知,节点出现在波矢为kc的位置,对应的能量简并本征态为

这些本征态满足:

这说明本文第一类相边界的节点受到一步平移对称性和子格子反演对称性的保护.

5 结论

本文提出了利用transmon 比特实现耦合强度独立可调的双链SSH 模型的可行性实验方案,发现了拓扑绝缘体和两类不同拓扑性质的相边界.构建模型时,本文首先设计了电容耦合的双链transmon 比特,然后用两个交流微波驱动每一个transmon 比特,从而实现比特间耦合强度的独立调控,最后通过改变比特间耦合参数实现交错的双链SSH 模型.双链SSH 模型是探索拓扑物态的重要模型之一,本文提供了一种构建双链SSH 模型的新途径.接下来探索了交错双链SSH 模型的拓扑性质,首先计算了k空间中双链SSH 模型的本征能量,并发现了两种类型的相边界.之后在参数空间中画出了拓扑相图,发现了两类拓扑绝缘相,其拓扑数分别为1 和—1,对应有两类边界态.拓扑相图也进一步给出了两类相边界的分布以及它们两侧拓扑数的值.最后分析了两类相边界的拓扑性质.本文将布洛赫态映射为k空间的矢量场,发现第一类相边界两个能带节点处的矢量场有两个扭结.两个节点的拓扑荷分别为1 和—1,并且受到平移和反转对称性的保护.另外,本文发现第二类相边界的能带节点处的矢量场不存在扭结,节点是拓扑平庸的.本文的结果填补了超导量子电路系统中实现双链SSH 模型的空白,并为探索链条型物理系统、拓扑物态以及节点型拓扑半金属提供了新的途径.