基于PSO-BP优化MPC的无人驾驶汽车路径跟踪控制研究*

史培龙 常宏,2 王彩瑞 马强 周猛

（1.长安大学，西安 710064；2.比亚迪汽车有限公司，西安 710119）

主题词：无人驾驶 路径跟踪控制 模型预测控制 粒子群寻优 BP神经网络

1 前言

无人驾驶汽车的关键技术包括环境感知、决策、运动规划和跟踪控制等。其中路径跟踪的目标是在保证行驶稳定性的前提下，使被控车辆沿着期望的路径行驶。目前常用的路径跟踪控制方法有斯坦利（Stanley）前轮反馈控制[1]、比例积分微分（Proportional Integral Derivative，PID）控制[2]、滑模控制[3]、线性二次最优（Linear Quadratic Regulator，LQR）控制[4]以及模型预测控制（Model Predictive Control，MPC）[5]等算法，MPC以车辆动力学模型作为预测模型，加入约束条件，能够显著提高控制精度。

Falcone 等[6]基于线性车辆模型建立了MPC 路径跟踪控制器，并对轮胎侧偏角进行约束，提高了车辆在低附着路面上的跟踪精度及稳定性；龚建伟等[7]利用MPC 算法进行路径跟踪，通过离散变步长，提高车辆高速行驶时的跟踪实时性，同时考虑了车辆操纵稳定性问题；张睿等[8]采用基于非线性预测及沿轨迹线性化的MPC 算法，提高了路径跟踪的实时性以及车辆在低附着系数路面条件下的跟踪精度。然而，上述研究并未考虑跟踪控制器时域参数对控制效果的影响。刘溯奇等[9]针对不同车速下恒定预测时域跟踪误差大的问题，设计了适用于变车速、变预测时域的MPC 控制器，以此提高控制精度；白国星等[10]设计了可变预测时域的MPC 路径跟踪控制器，利用三次多项式拟合最佳预测时域与速度的关系，在不同车速下使用不同的预测时域参数，提高了控制器对速度的自适应性。但是，上述研究忽略了不同路面附着系数与时域参数的关系。吴施鹏等[11]基于MPC 算法，利用遗传算法获得最优时域参数，提高了车辆在低附着路面条件和高速行驶时的行驶稳定性；范贤波等[12]采用模糊控制法对MPC 控制器的预测时域及控制时域进行在线优化，根据车辆的横向及纵向车速自适应选择预测时域参数，优化后的MPC 控制器提高了车辆路径跟踪的稳定性及跟踪精度。但对时域参数进行在线优化会增加MPC 的计算量，影响控制器的实时性。

综合考虑时域参数、路面附着条件及控制时效性对控制效果的影响，本文利用粒子群寻优-反向传播（Particle Swarm Optimization-Back Propagation，PSO-BP）离线优化MPC 控制器的预测时域和控制时域参数，通过在不同路面附着系数及车速条件下自适应选择最优时域参数，保证控制器具有较好的效果。

2 车辆动力学模型

汽车是高度非线性的复杂系统，车辆模型越复杂，其仿真结果越接近真实运动规律，但当系统模型复杂时，计算量增加，会降低控制器的时效性，影响跟踪效果，甚至引发危险。为此，本文对车辆模型进行简化，建立了三自由度车辆动力学模型[13]，如图1 所示。建模过程考虑了转向轮轮胎的侧偏特性，忽略了垂向运动、空气动力学特性、横向载荷及前、后轴荷转移带来的影响。

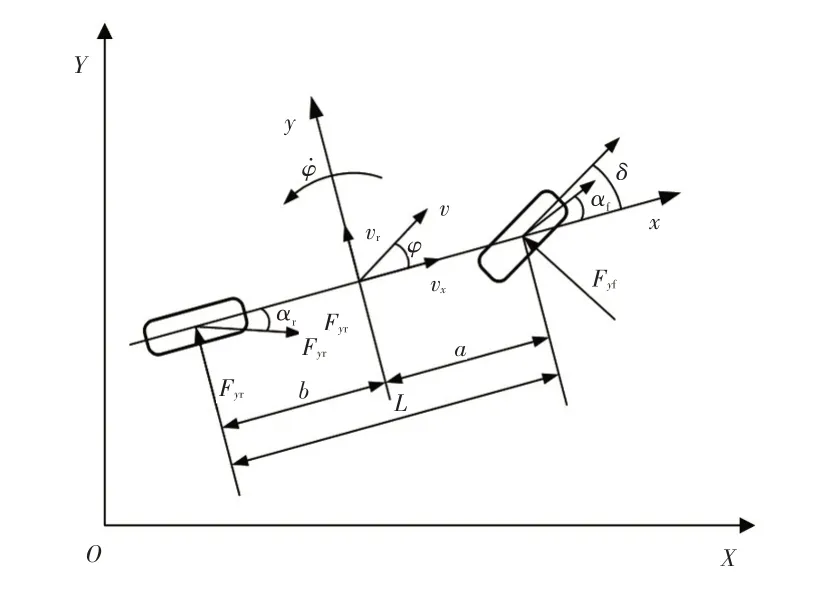
图1 三自由度车辆动力学模型

由牛顿第二定律可得：

式中，m为整车整备质量；φ为车辆的航向角；Fxf、Fxr分别为前、后轴轮胎的纵向力；Fyf、Fyr分别为前、后轴轮胎的侧向力；vx、vy分别为质心的纵向及横向速度；Iz为绕z轴的转动惯量；a、b分别为质心到前、后轴距离。

大地坐标系与车身坐标系的转换以及车辆动力学模型为：

式中，Ccf、Ccr分别为车辆前、后轮侧偏刚度；Clf、Clr分别为前、后轮胎纵向刚度；Sf、Sr分别为前、后轮胎纵向滑移率；δf为前轮转角；X、Y为车辆在大地坐标系下的纵向、横向位置。

3 基于PSO-BP优化的MPC跟踪控制器设计

3.1 MPC路径跟踪控制器设计

3.1.1 MPC控制器

MPC由预测模型、滚动优化和反馈校正3个部分组成，其流程如图2所示。MPC控制器依据预测模型及目标函数进行最优求解，得到最优序列u(t)并输出，通过滚动优化、反馈校正保证被控车辆沿着期望路径行驶。考虑到车辆模型的非线性特性，为了提高控制精度，本文基于非线性MPC模型进行路径跟踪控制器设计。

图2 基于MPC的路径跟踪控制流程

3.1.2 预测模型及其离散化

本文采用三自由度车辆动力学模型作为控制器的预测模型。式（2）经状态转换，得到系统状态为：

系统输出量η为：

η的构造公式为：

3.1.3 目标函数与约束条件设计

考虑到跟踪过程中车辆的稳定性，为车轮转角变化量和跟踪误差分别赋予权重，建立目标函数。设控制器预测时域为Np，控制时域为Nc，建立目标函数：

式中，ηref(k+i)、η(k+i)分别为以当前时刻k起，预测时域Np内第i个时刻的期望输出量、输出量预测值；ρ为常量；ε为松弛因子；Q、R分别为跟踪过程中准确性和平稳程度的权重。

式（7）中第1 项为系统输出与期望轨迹间的偏差，表征无人驾驶汽车路径跟踪的准确性，第2项为系统输入的变化量，表征车辆路径跟踪过程中的平稳程度。为获得最优解，目标函数改写为：

为了防止控制量超出范围，对输出的前轮转角和增量进行约束：

式中，Umin、Umax分别为车轮转角的最小值和最大值；ΔUmin、ΔUmax分别为车轮转角增量的最小值和最大值。

3.2 路径跟踪控制器设计

3.2.1 评价指标

为了保证控制精度和车辆行驶稳定性，建立评价函数，判断时域参数Np和Nc的优劣。文献[14]以平均横向偏差、最大偏差和平均横摆角偏差作为路径跟踪准确性评价指标，文献[15]以质心侧偏角和横摆角速度作为车辆行驶稳定性的评价指标。为此，本文选择平均横向偏差emean、最大横向偏差emax、最大质心侧偏角βmax和最大横摆角速度作为路径跟踪过程评价指标。

路径跟踪时，emean、emax越小，控制器精度越高；βmax、超过路面允许值[16]时，车辆将失稳。βmax、、车速及路面附着系数存在约束关系：

式中，g为重力加速度；μ为路面附着系数；v为车辆行驶速度。

为了消除不同量纲的影响，将评价指标emean、emax、βmax和进行归一化处理。用最大横向偏差和平均横向偏差归一化总和E表征控制器的控制精度；用最大横摆角速度、最大质心侧偏角归一化总和W表征行驶稳定性。

考虑到Np较大时，能够预测未来更多信息，转向动作时间充裕，车辆行驶稳定性较好，但控制精度会降低，因此一组Np和Nc控制参数难以保证控制精度E和稳定性W同时达到最小。为此，设计评价函数S，获得最优时域参数时，能够兼顾控制器控制精度和跟踪时车辆的行驶稳定性的时域控制参数：

式中，A为控制精度E的权重；B为稳定性W的权重。

3.2.2 基于PSO-BP的MPC时域参数优化策略

为了获得不同路面附着系数及车速下的最优时域控制参数，本文提出基于PSO-BP 算法的MPC 优化策略，如图3 所示。首先，训练基于BP 神经网络模型，输入层为时域控制参数Np、Nc、路面附着系数μ和车速v，输出层为控制精度E和稳定性W；其次，在不同μ和v条件下产生粒子群，并赋予粒子不同的时域控制参数Np、Nc，再次获得E和W；通过不同的Np、Nc进行迭代寻优，利用评价函数S判断Np、Nc是否为最优时域参数，直至达到最大迭代次数，并输出最优时域参数，由MPC控制器进行路径跟踪控制。

图3 基于PSO-BP算法的MPC优化策略

3.2.3 不同时域参数下试验数据获取

为了获取最优时域参数Np、Nc，利用设计的MPC 路径跟踪控制器获取试验数据，并对数据进行分析处理。在路面附着系数μ=0.4，车速分别为18 km/h、36 km/h 和54 km/h低、中速条件下，以及μ=0.8，车速分别为18 km/h、36 km/h、54 km/h、72 km/h 和90 km/h 低、中、高速条件下，利用遍历的方法，对不同时域参数Np和Nc的MPC控制器进行仿真，得到评价指标emean、emax、和βmax。Np的取值范围为15～36，Nc的取值范围为1～Np-1，剔除异常值后获得数据4 094组，训练数据结构如图4所示。

图4 训练数据结构

3.3 BP神经网络训练

利用获取的试验数据训练BP神经网络，其中80%的数据作为训练集，剩余20%的数据作为测试集。输入层为路面附着系数μ、车速v以及时域控制参数Np和Nc，输出层为控制器控制精度E和车辆行驶稳定性W，隐藏层数为3层，每层神经元数量为50个，最大迭代次数为1 000次，最大均方误差为0.000 01，训练迭代过程如图5所示。

图5 BP神经网络训练效果

由图5 可知，第378 次迭代时，均方误差9.991×10-6小于0.000 01，停止迭代，此时相关性系数R=0.999 96，拟合效果较好。此时，输出控制精度E和稳定性W的训练集拟合效果和测试集预测效果如图6和图7所示，控制精度E训练集及测试集拟合最大误差分别为0.038和0.062，稳定性W训练集及测试集拟合最大误差分别为0.023 和0.051，真实值与预测值基本吻合，表明神经网络训练和测试效果较好。

图6 控制精度E神经网络训练和测试结果

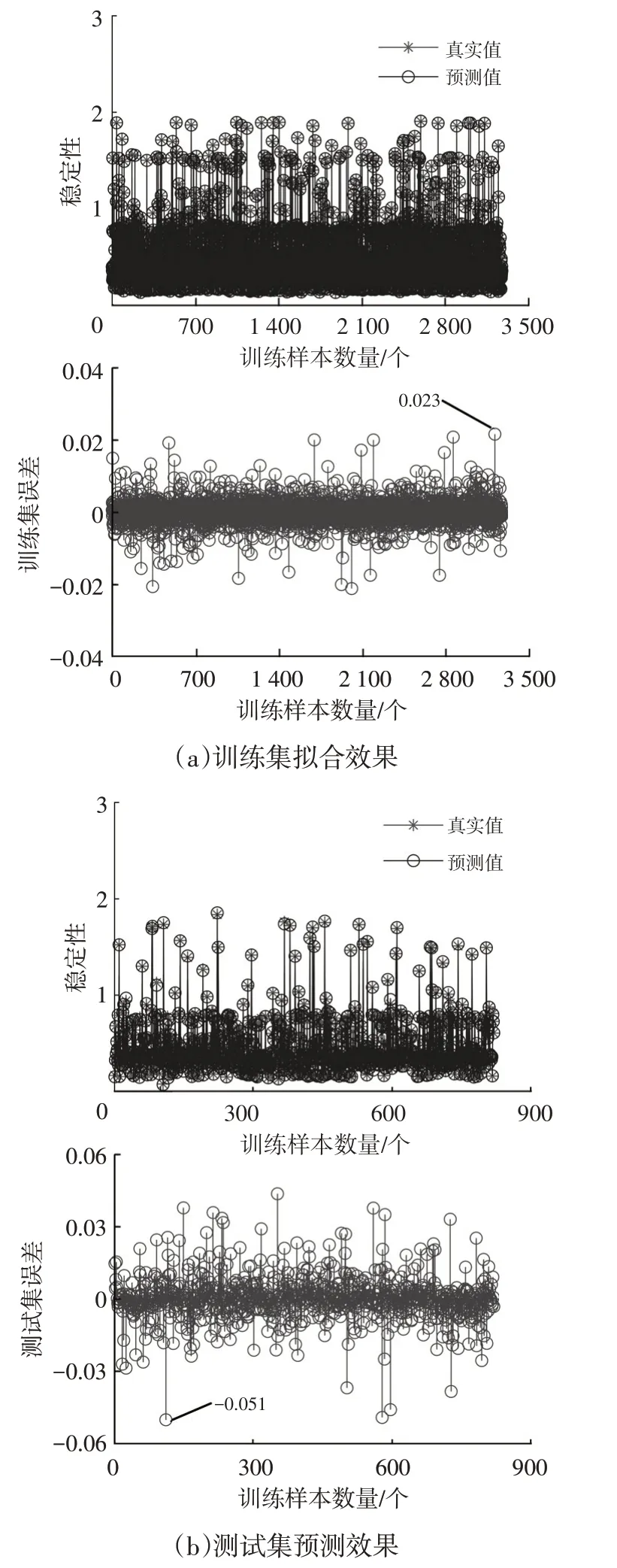
图7 稳定性W神经网络训练和测试结果

4 基于PSO-BP优化的MPC控制器仿真验证

为了验证本文设计控制器的实际效果，分别进行低路面附着系数低速工况、高路面附着系数低速和高速工况及中路面附着系数中速工况双移线跟踪仿真对比验证。考虑实际运行安全因素，取目标函数权重A=8、B=2。

4.1 低路面附着系数低速工况双移线跟踪仿真

设置路面附着系数μ=0.4、车速v=40 km/h，利用PSO-BP 算法得到Np=15、Nc=7；选择对比验证固定时域参数Np=25、Nc=10。将参数输入MPC控制器进行仿真，各评价指标如表1所示，跟踪效果及跟踪偏差如图8所示，质心侧偏角及横摆角速度如图9所示。

表1 低附着低速工况仿真结果

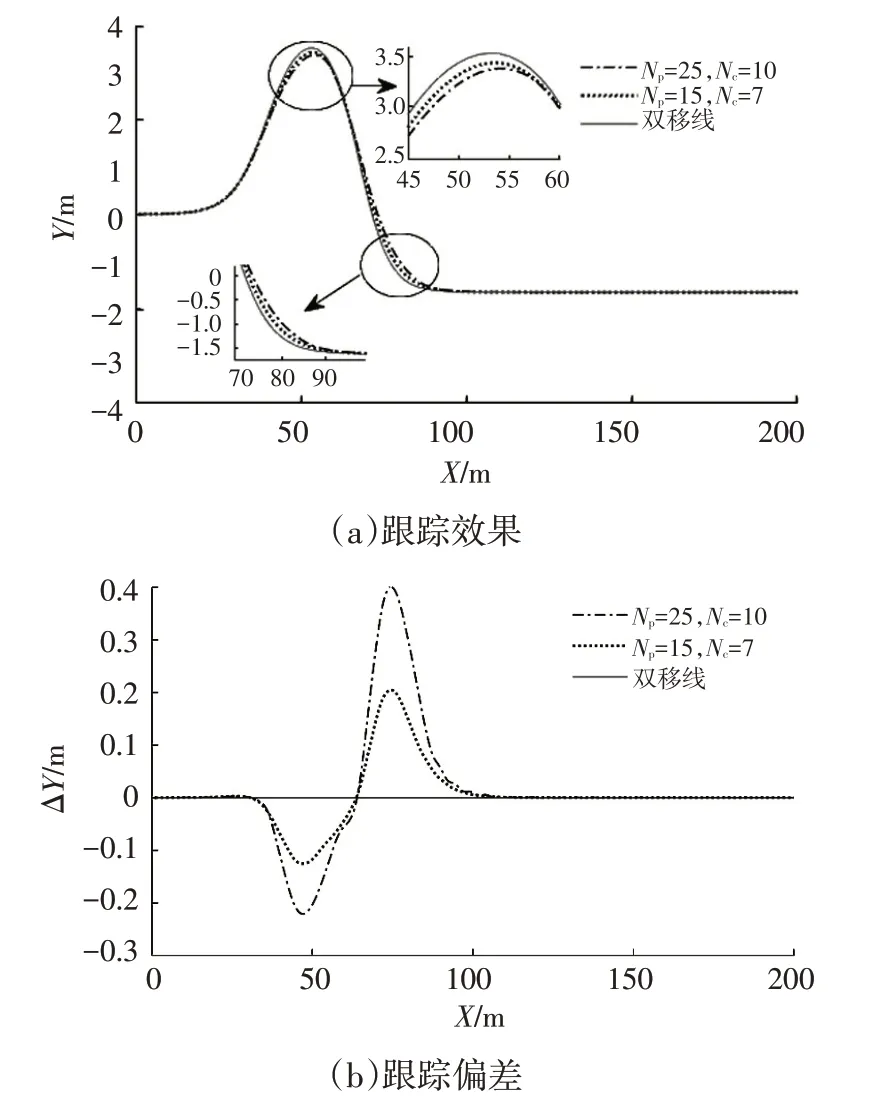
图8 低附着低速工况跟踪效果及横向偏差

图9 低附着低速工况质心侧偏角及横摆角速度变化

由表1可知，固定时域MPC横向偏差的最大值和平均值均大于PSO-BP优化的MPC对应值，其最大值分别为0.400 5 m 和0.204 7 m，后者降低了近50%。仿真结果显示，PSO-BP优化的MPC控制器最大质心侧偏角和最大横摆角速度较固定时域MPC 控制器大，但二者仅相差0.014°和0.042(°)/s，因为后者采用了较大的时域控制参数，车辆稳定性相对增加，但横向偏差较大。由图8 可知：PSO-BP 优化的MPC 控制器控制车辆跟踪的横向偏差始终小于固定时域MPC作用时的横向偏差；2种控制器分别作用时，质心侧偏角及横摆角速度相差较小，均能保证车辆进行路径跟踪时的稳定性，如图9 所示。由此可见，PSO-BP优化的MPC路径跟踪控制策略能够提高路径跟踪精度。

4.2 高路面附着系数低速工况双移线跟踪仿真

设置路面附着系数μ=0.8、车速v=40 km/h，利用PSO-BP 算法得到Np=12、Nc=3；选择对比验证固定时域参数Np=25、Nc=10。将参数输入MPC控制器进行仿真，各评价指标如表2所示，跟踪效果及跟踪偏差如图10所示，质心侧偏角及横摆角速度如图11所示。

表2 高附着低速工况仿真结果

图10 高附着低速工况跟踪效果及横向偏差

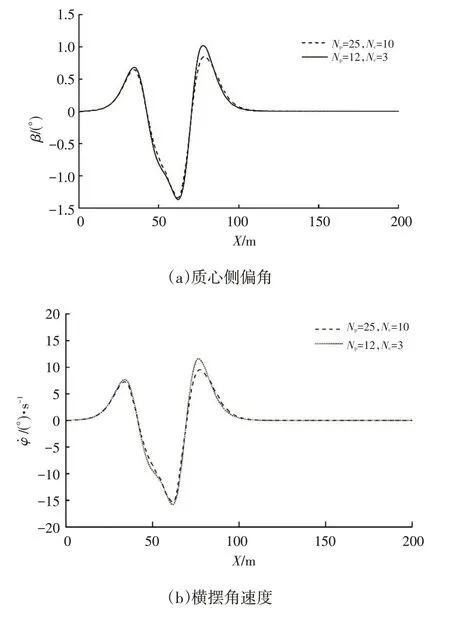
图11 高附着低速工况质心侧偏角及横摆角速度变化

由表2可知，固定时域MPC横向偏差的最大值和平均值均大于PSO-BP优化的MPC对应值，其最大值分别为0.351 7 m 和0.157 8 m，后者降低了55%。仿真结果显示，PSO-BP优化的MPC控制器最大质心侧偏角和最大横摆角速度较固定时域MPC 控制器略大，但其仅相差0.226 7°和0.455 8(°)/s，因为后者采用了较大的时域控制参数，车辆稳定性相对增加，但其横向偏差较大。由图10可知：PSO-BP优化的MPC控制器控制车辆跟踪的横向偏差始终小于固定时域MPC 作用时的横向偏差；2 种控制器分别作用时，质心侧偏角及横摆角速度相差不大，均能保证车辆进行路径跟踪时的稳定性，见图11。由此可见，PSO-BP优化的MPC路径跟踪控制策略能够提高路径跟踪精度。

4.3 高路面附着系数高速工况双移线跟踪仿真

设置路面附着系数μ=0.8、车速v=80 km/h，利用PSO-BP 算法得到Np=36、Nc=21；选择对比验证固定时域参数Np、Nc不变。将参数分别输入控制器进行仿真，得到仿真结果如表3、图12及图13所示。

表3 高附着高速工况仿真结果

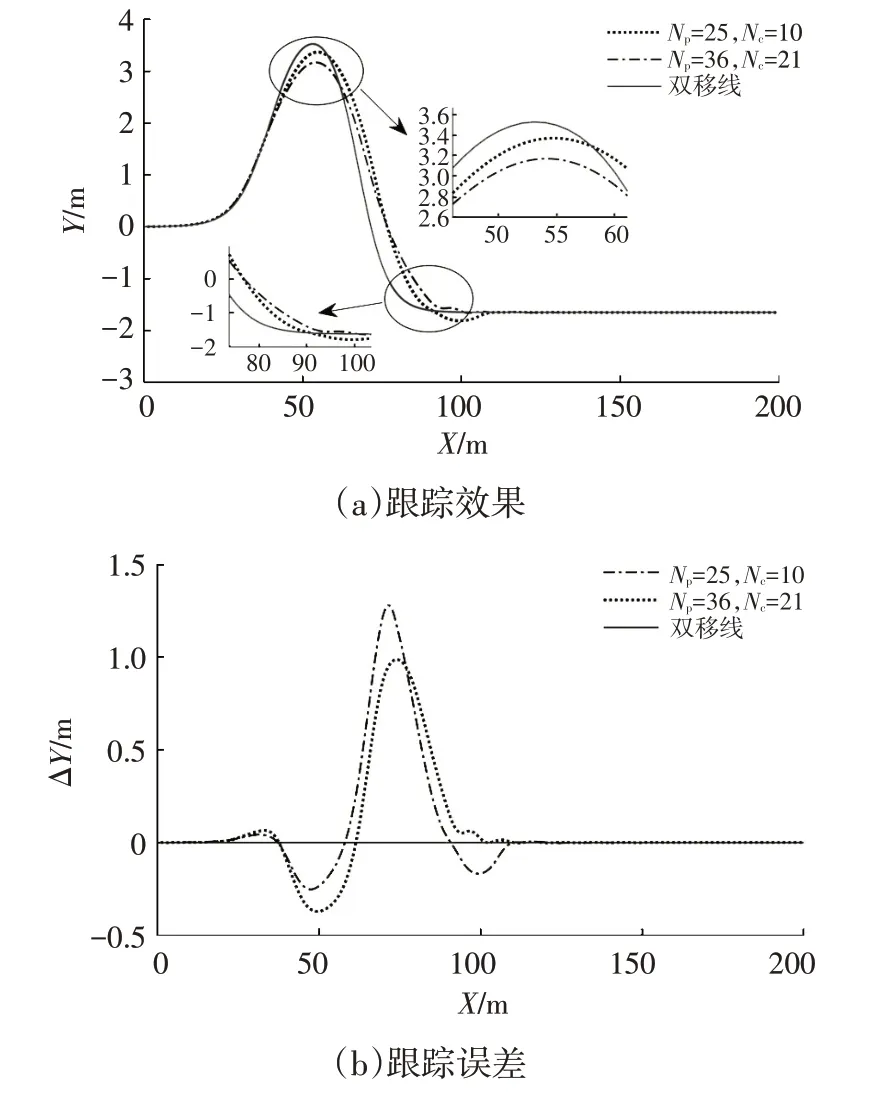
图12 高附着高速工况跟踪效果及横向偏差

图13 高附着高速工况质心侧偏角及横摆角速度变化

由表3可知：相比于固定时域MPC，PSO-BP优化的MPC各项评价指标均小于前者；前者横向偏差较大，控制精度较低，最大质心侧偏角接近10°，最大横摆角速度达到39.476(°)/s，车辆行驶稳定性较差，可能产生侧滑等危险。

4.4 中路面附着系数中速工况双移线跟踪仿真

设置路面附着系数μ=0.6、车速v=60 km/h，利用PSO-BP 算法得到Np=19、Nc=9；选择对比验证固定时域参数Np、Nc不变。将参数分别输入控制器进行仿真，得到仿真结果，如表4、图14及图15所示。

表4 中附着中速工况仿真结果

图14 中附着中速工况跟踪效果及横向偏差

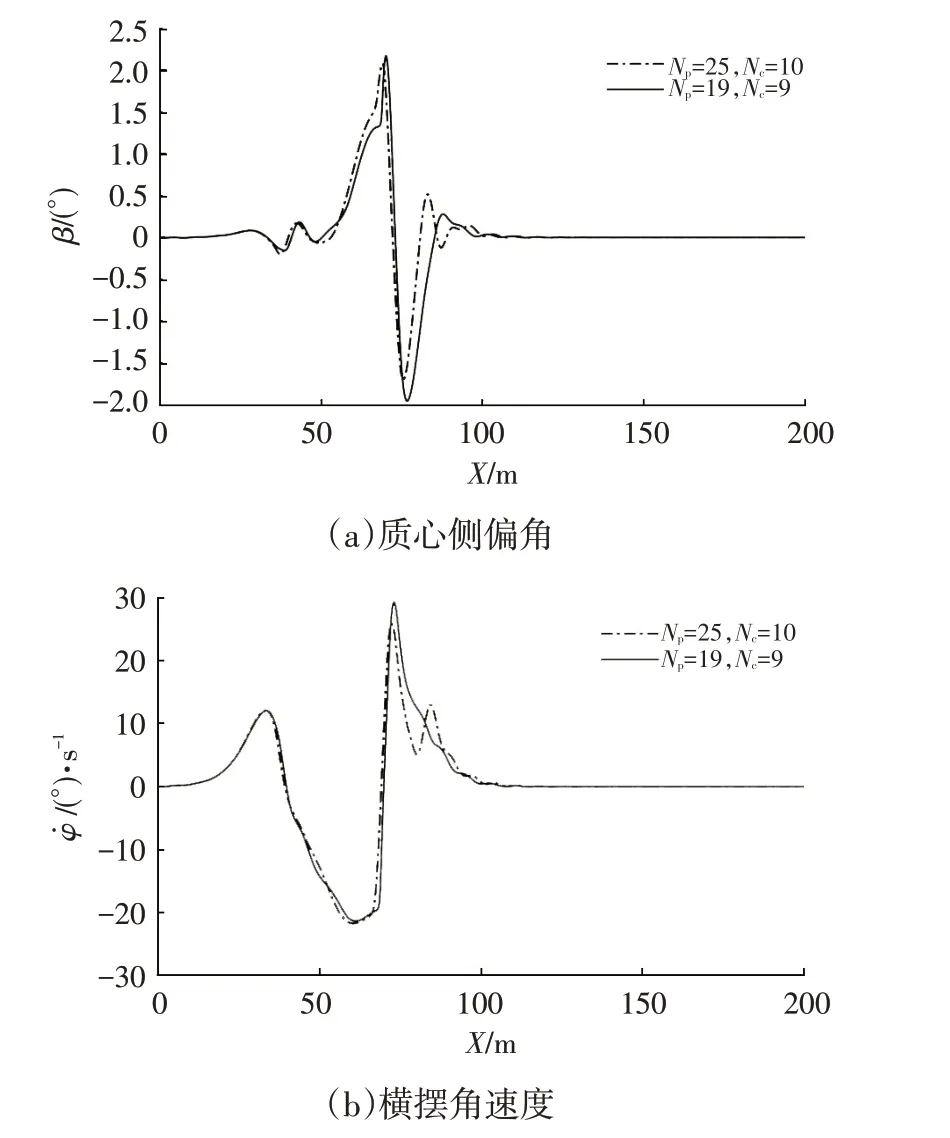
图15 中附着中速工况质心侧偏角及横摆角速度变化

由表4可知，固定时域MPC横向偏差最大值和平均值均大于PSO-BP 优化的MPC 对应值，分别为0.531 m和0.441 m，最大质心侧偏角和最大横摆角速度小于后者，但是后者显著提高了跟踪精度，如图14所示。由图15 可知，后者最大质心侧偏角和横摆角速度分别为2.168°和20.457(°)/s，车辆处于稳定状态，在保证车辆稳定性的前提下，能够提高跟踪精度。

4种工况下双移线跟踪仿真验证结果表明：车辆以中低车速行驶时，基于PSO-BP获得时域参数的MPC控制器，能够在保证车辆行驶稳定性的前提下提高控制器的跟踪精度；车辆高速行驶时，利用PSO-BP 优化算法获得时域参数的MPC 控制器，不仅能够提高控制器的跟踪精度，还能提高车辆的行驶稳定性。

5 结束语

为了兼顾时域参数、路面附着条件及控制时效性对无人驾驶汽车路径跟踪控制效果的影响，本文提出了基于PSO-BP优化的MPC路径跟踪控制策略，并在低路面附着系数低速、高路面附着系数低速、高路面附着系数高速及中路面附着系数中速工况下验证了控制效果，得出以下结论：

a.PSO-BP优化后的MPC控制器路径跟踪过程中，高附着、低附着路面低速工况下横向控制精度提高了50%以上；中速工况和高速工况下横向控制精度分别提高了20%和9%。

b.基于PSO-BP 优化的MPC 路径跟踪控制策略能够依据路面附着条件和车速自适应Np、Nc参数，与固定时域参数相比，不仅能提高车辆路径跟踪精度，还能兼顾车辆行驶稳定性。

c.利用PSO-BP 离线优化MPC 控制器的预测时域和控制时域参数，利用BP神经网络泛化能力，降低在线数据复杂程度，可有效提高控制的时效性。

本文BP 神经网络训练样本附着系数只有0.4 和0.8，后续研究工作需要进一步优化；控制策略仅在仿真环境验证，需要进一步开展实车验证。