既有网壳结构显著构件损伤识别方法

吴 俊

(同恩(上海)工程技术有限公司, 上海 200433)

0 引 言

随着既有结构的逐渐老化,加之不间断的服役使用,为避免在未来可能造成的灾难性后果,对既有结构进行损伤评估的需求受到高度重视。由于既有结构损伤情况的复杂性和隐蔽性,使用传统的检测手段很难确定损伤的精确位置和损伤程度。特别是对于具有海量构件和节点的既有网壳结构,更是难以通过检测每一根构件或节点的方式来识别损伤。与此同时,由于大多数既有结构均处于服役状态,使用具有破坏性的有损检测方法不是理想手段,往往也不被允许。基于此,许多学者在过去二十年来提出了多种用于识别损伤构件或节点的无损识别技术[1-3],其中包括了整体结构的损伤识别技术[4-7]以及一些聚焦于局部构件[8]或节点[9]的识别方法。

其中一类常见的无损识别方法是基于结构模型矩阵修正(例如质量、阻尼即刚度矩阵)的模型更新技术[10-11]。Zimmerman等首次提出了一种更新结构刚度矩阵的最小秩摄动理论[12-13]。随后,Kaouk等又提出了最小秩摄动理论的结构质量矩阵更新方法[14]。Mares等利用了遗传算法来识别弹性结构中的构件损伤位置和损伤程度[15]。该方法的假定前提是结构处于弹性阶段,但是当结构发生累积损伤后,往往伴随着几何非线性或材料非线性,因此该假定的适用范围是非常有限的。Rao等进一步发展了遗传算法在结构损伤识别领域的应用,将其用于识别振动物体的损伤[16]。该方法通过引入结构刚度折减系数,对理想的有限元模型进行参数化建模。利用遗传算法的特性,有限元模型的刚度折减系数可以通过最小化总体方差的方式进行定参。Meruane等提出了一种混合实数编码的遗传算法[17],通过损伤“惩罚”,可以确定桁架结构中的损伤位置和程度。这种改进的遗传算法的特点在于不需要完整测量桁架结构的所有自由度,便能提供相比于传统方法而言更为精确的解决方案。Perera等考虑了单元弯曲刚度的折减系数,提出了一种遗传算法来预测梁的损伤位置和严重程度[18]。Perera等考虑到建模误差,通过群体优化对多目标损伤识别进行了改进,从而改进了遗传算法[19]。

结构自振频率和振型亦可作为模型更新的参数,从而进行结构损伤识别。通过该方法,Weber等提出了一种损伤检测方法[20],通过正则化模型更新的手段逼近真实结构模型。Kaveh等提出了一种改进的带电系统搜索算法(CSS)识别桁架结构的损伤[21]。Esfandiari等提出了一种基于自振频率的刚度折减方法识别结构损伤[4]。该方法中,自振频率被表征为刚度折减的函数,结构模态的变化被表征为一组理想结构模态的线性组合。

然而,基于频率和模态的损伤识别方法存在噪声或测量误差等问题[22-23]。在损伤识别过程中若忽略这些误差特征往往会造成错误的识别结果[24]。为此,寻找一种不被测量噪声误差影响的稳定特征值将有利于提高损伤识别的精度。而利用依赖于载荷的Ritz向量作为模态向量的替代品,被证明可用于结构的损伤识别。Cao等提出了一种Ritz向量的提取技术[25],可通过单台或多台振动台测试来提取结构的Ritz向量。即使如此,仍然很难直接从振动测试中识别Ritz向量。Sohn等提出了一种基于柔度矩阵的方法[26-27]从测得的振动数据中提取Ritz向量,并可采用一种贝叶斯概率方法利用Ritz向量对结构进行损伤识别检测。Taylor等提出了一种用于非正交Ritz向量提取的改进算法[28],可以更准确地识别结构构件损伤位置和程度。Ritz向量由于采用了依赖于线性代数方程组的求解方法,而非矩阵特征向量的求解,因此其对测量过程中的噪声和误差敏感度远低于模态向量。鉴于上述事实,Ge等利用残余力方法定位结构中的损伤区域[29]。Yang等发展了残余力方法,利用不完全测量的模态参数进行损伤识别[30]。但是,该方法将结构损伤视为节点自由度方向上的刚度降低,导致计算结果不能直接用于识别构件损伤。Yun等改进了一种基于动态残余力测度的参数子集选择方法[31],用于多构件损伤定位,但该方法的应用受到结构尺度的限制。

本文提出一种用于既有网壳结构显著损伤构件识别的改进残余力向量分解法(简称RFD),可以根据测量获取的网壳结构固有特征向量的变化识别损伤特征。通过定义的沿构件轴向投影方向上的无量纲模态变形,可以将所测得的特征向量采用改进残余力向量分解法转化为一组多元线性方程组,用以定位具有显著刚度折减情况的构件。根据网壳结构构件和节点数目的相对关系不同,讨论了3种计算条件,特别是当多元线性方程组的解不唯一时,利用Ritz向量的灵敏度分析和模态置信准则(MAC)筛选出网壳结构的次要构件,并作为附加约束条件引入。与框架或桁架结构不同,网壳结构模态参与质量比(MPMR)不会随着模态阶数的增加而有规律地降低[32]。同时,通过构造网壳结构算例,阐述改进残余力分解法的计算过程并验证其有效性。

1 改进残余力分解法

网壳结构是一种刚性空间结构,其整体形状是一个空间曲面,结构中的每一根构件均是直杆,网壳结构同时兼具桁架和壳体的特征。从宏观角度来看,网壳结构的力学特征更接近于壳,结构所受的外部荷载主要通过面内轴向薄膜力平衡和传递,如图1所示。因此,网壳结构的整体稳定承载能力,特别是单层网壳结构,对构件的损伤更为敏感。基于网壳结构的力学特性,本文采用以下假定进行损伤识别分析。

假定1:对于既有网壳结构,其服役阶段的荷载主要由面内薄膜力和面外弯矩(在其失稳之前)所平衡,因此,网壳结构中的构件主要均承受轴向力,面外弯矩可以忽略,在损伤识别过程中可主要考虑轴向刚度。

假定2:既有网壳结构的大多数构件在服役期间均处于弹性阶段,因为网壳结构的承载能力大多通常由其整体稳定承载力所主导,因此,可假定既有网壳结构的构件在损伤识别分析过程中保持弹性,而不考虑塑性效应。

假定3:在损伤识别过程中,既有网壳结构的外部荷载及其等效质量是可以被统计的。本文所提出的改进残余力分解法不考虑结构损伤过程中的质量变化。

假设构件损伤对既有网壳结构质量特征矩阵的影响可以忽略不计,则具有p个测量模态的n个自由度无阻尼结构的特征值问题可以表达为:

[(Ku-ΔK)-λjMu]{φ}j=0

(Ku-λjMu){φ}j=ΔK{φ}jj=1,2,…,p

(1)

式中:Mu为既有网壳结构的质量矩阵,在损伤识别过程中可认为其保持恒定;Ku为既有网壳结构未损伤情况下的刚度矩阵,实际情况下很难精确获得完善结构未损伤情况下的刚度矩阵,可采用理想有限元模型代替未损伤结构;λj和{φ}j分别为既有网壳结构有损伤情况下的第j阶特征值和相应的特征模态向量;ΔK为对应于结构刚度折减的整体刚度摄动矩阵,用于表达结构真实刚度矩阵和理想刚度矩阵之间的差值。令:

bj=(Ku-λjMu){φ}j

(2)

式中:bj为第j阶残余模态力。

将式(2)代入式(1),得:

ΔK{φ}j=bj

j=1,2,…,p(3)

可知,一旦确定了结构第j阶自振频率和模态,则bj便可确定。

本文的目标是计算获得杆件刚度折减的相对程度,因此,整体刚度摄动矩阵ΔK可以用参数化的方式表达,即:

(4)

r={rs}

s=1,2,…,N(5)

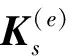
图2 RFD方法的计算概念示意Fig.2 The calculation concept schematic of RFD method

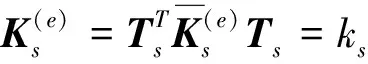
(6)

其中

ks=EsAs/ls

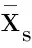
(7)

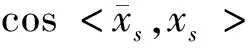
将式(4)、式(6)代入式(3)中,则与构件s相关的残余模态力向量可表示为:

(8)

式中:bj,m,s,bj,n,s分别为节点m,n的残余力向量。

式(8)可以进一步分解为:

(9)

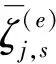
(10)

(11)

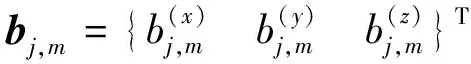
式中:Nm为与节点m相连的结构构件数量;bj,m为节点m的残余力合向量;sign(s)为符号函数,当构件s的局部坐标方向始于节点m,则sign(s)=-1,否则sign(s)=1;同理,对于节点n,表达式意义相同。进一步地,式(11)可以简化为:

(12)

考虑到结构中所有M个节点,式(12)可以被进一步表达为方程组的形式:

(13)

式中:Nm为与节点m(m∈[1,M])相连的所有构件数量,对应于方程第m行。值得注意的是,式(5)中的参数集r={rs}(损伤系数)在这里是未知量,是方程(13)的自变量。由于方程式中仍然存在耦合的未知参数而难以直接求解,因此,进一步假设每一个节点都与所有构件相连,则方程(13)可以被表达为:

(14)

式中:M为节点总数;N为构件总数;A3M×N为方程的系数矩阵的代号。如果构件s与节点m不相连,则参数km,s=0,否则km,s=ks。方程(14)可以被理解为残余力向量bj,m的分解,以平衡由于损伤而引起的残余模态力(图2)。求解方程(14),则可得到损伤系数r={rs}的原始解。

2 改进RFD方法的计算条件

2.1 构件重要性

利用整体结构的质量矩阵和刚度矩阵计算的Ritz向量对结构刚度敏感,这是因为其优势在于每一个Ritz向量都描述了涵盖一部分范围内的结构频率和模态向量[28]。因此,当某个构件刚度降低时,解析Ritz向量将产生相对于理想结构的特定扰度。构件对结构刚度的贡献越大,则Ritz向量的扰度越明显。因此,解析Ritz向量的扰度可以作为构件重要性的指标。一个n自由度(nDOF)无阻尼结构模型的振动方程可以表示为:

(15)

式中:K和M分别为结构刚度和质量矩阵;p为代表输入力空间分布的n×1向量。第一个Ritz向量v1可用质量归一化结构在以向量p形式静力荷载作用下的静态变形表示,其表达式为:

(16a)

(16b)

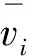
(17)

经过Gram-Schmidt正则化[33]和质量归一化,可以得到线性独立的Ritz向量vi,即:

(18a)

(18b)

令V0为完善结构的Ritz向量集合,即:

V0={v1,v2,…,vz}0

(19)

式中:z为扩展的Ritz向量集合的数量。如果一个构件s刚度降低,则Ritz向量集可以(MAC准则)表达为:

(20)

式中:rs为构件s的刚度折减系数,与前述概念相同。模态保证准则(MAC准则)[34]是模态向量相似性分析的方法之一。MAC准则有3个等效公式来评估相似性,其中之一可用于向量集,其等效公式表达为:

(21)

式中:{vj}0为完善结构Ritz向量集中第j阶向量;{vj}s为单元s刚度降低后的结构Ritz向量集中第j阶向量;IC(s)为构件s的重要性系数,即若构件s的刚度折减对Ritz向量的扰动程度越小,则A(V0,Vs)值越接近于1,构件s的重要程度也越低。

2.2 附加约束确定方法

对于既有网壳结构而言,方程组(14)的系数矩阵A3M×N在通常情况下不是一个方阵。因此,整个计算过程将分为3种情况。1)如果系数矩阵的秩小于N,方程组将得到无穷解,计算过程中需要引入附加约束使结果具有唯一性;2)如果3M≥N且rank(A3M×N)=N,则方程组具有唯一解,无须附加约束;3)若3M≥N且rank(A3M×N)>N,这是一个过拟合问题,可通过最小二乘法来求解。本节将主要讨论第一种需要附加约束的情况。

假设一个构件对结构整体刚度几乎没有贡献,那么该构件即使严重损坏也很难被识别。因此,可以合理地假设结构中最不重要的构件没有损坏,并将其作为方程求解的附加条件。由前文可知,对于构件s的重要性程度,可通过式(21)计算其重要性系数IC(s)来表征。计算所有构件的重要性系数后,按升序排列,IC值越大,其构件重要性程度越高。若IC=1,则表示构件对结构刚度没有贡献。而后,从低到高逐个选择重要性系数最低的构件,将其损伤系数rs设为0,以作为求解损伤系数方程组的附加约束。作为附加约束的构件数量由求解方程组的系数矩阵A3M×N的秩而定,即:

ri=0

i=1,2,…,n(22)

其中n=N-rank(A3M×N)>0

根据上述过程,将这n个最不重要构件的损伤系数rs值设置为0是合理的,因为这些构件的刚度贡献太小对整体结构刚度没有影响。随后,可通过联立等式(14)和式(22)来求解损伤系数DP值。

2.3 有效模态确定方法

由于所提出的改进RFD方法的推导过程是基于第j阶模态向量,因而,其应用显然受到模态选择的影响。传统高层结构的模态特征一般由前几阶模态控制,但既有网壳结构的模态特征与传统高层结构非常不同,呈现簇状模态分布,甚至在几十阶后的模态仍有可能对网壳结构产生较大影响,因而难以直接选择前几阶作为有效模态,因此,针对既有网壳结构,非常有必要讨论如何确定合适并且有效的模态作为损伤识别的输入条件。通常,将模态质量参与系数(MPMRs)[35]用作有效模态选择的参数:

(23)

式中:{φj}为第j阶模态向量;{dr}为模态方向r的单位向量。

与传统多高层结构不同,网壳等空间结构的模态质量参与系数随着模态阶数的增加并不会有规律地下降。实例图3a给出了典型既有网壳结构的模态质量参与系数计算结果。可看出:模态质量参与系数并不是随着模态阶数增加而递减的。值得注意的是,图3a、图6a中的模态质量参与系数峰值均在高阶模态中出现。与此同时,现有试验结果表明,在模态试验中又很难激发网壳结构中MPMR值接近或等于0的模态。因此,针对网壳结构选择最低的n阶模态作为计算输入条件是不合理的,应通过确定一个合理的阈值δ,选择模态质量参与系数大于阈值的模态作为有效模态输入,即Ljr≥δ。采用每一种选择得到的模态,都可以用来计算一组结构构件损伤系数集合r={rs}。根据crossMAC准则[34],不同的模态对结构的不同损伤状况敏感程度是不同的,因此,应将每一种

被选择的有效模态都用作输入条件,损伤识别的最终结果取决于所有计算结果的综合分析。

3 实例分析

3.1 结构模型

本文设计了一个K6型单层网壳结构(图4)作为既有网壳结构算例来验证本文提出的RFD方法。结构的几何及物理参数见表1。结构由72根热轧无缝钢管构件(不包括四周环绕的支座之间的环向构件)和19个非支座节点组成。结构荷载包括球节点附加质量、屋面板及吊顶悬挂重量以及其他活荷载,均简化为节点集中荷载。

表1 模型参数Table 1 Model parameters

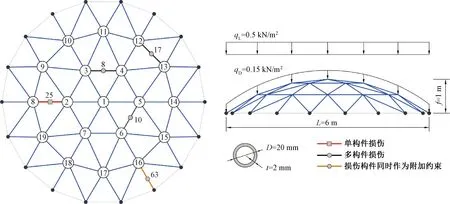
图4 K6型单层网壳结构模型Fig.4 Kiewitt-6 single-layer latticed shell structure model

算例中,非支座节点数量M=19,构件数量N=72,其结果为3M

1)依次削弱结构中每一根构件的轴向刚度,保持其余构件刚度不变。保证每一根被削弱的构件的刚度折减百分比相同,如20%。因为构件重要性系数的计算过程是线性的,因而只要各构件依次削弱的折减率相同,无论折减率取值大小,构件重要性的相对关系是不会改变的;

2)每一次构件刚度削弱后,计算前5阶Ritz向量;

3)根据式(21)计算并对重要性系数进行排序;

4)经升序排列后,选择最低IC值的前15根构件作为附加约束的构件。

3.2 单构件损伤识别

假定仅25号主肋杆构件发生严重损伤(图4),轴向刚度折减50%。在这种情况下,损伤后结构的动力特性及其MPMRs计算结果如图3a所示。为了筛选有效模态,将阈值设为10%。基于该条件,共筛选出5个有效模态,包括第8、9、19、21、22阶模态。对于每一个被筛选出的有效模态,在计算中考虑5%的随机噪声[30],用以模拟模态检测采集时的误差等,该噪声将直接叠加于模态数据中,如图3b所示。

联立等式(14)和式(22),则可计算出单损伤构件的K6型网壳结构损伤系数集(DPs),结果如图5所示。表明:模态8,9,21成功识别出了构件25的损伤,而模态9对该构件的损伤并不敏感;虽然模态22识别出了构件25的损伤,但却错误地将构件1识别成了严重损伤构件,可能的原因在于构件1与构件25的位置非常接近。因此可以得出结论,模态8,9,21对5%噪声干扰是稳定的,综合考虑上述识别结果,对于单一构件损伤的K6网壳结构,其损伤构件25可以被成功识别。

a—模态8; b—模态9; c—模态19; d—模态21; e—模态22。图5 单构件损伤识别的计算结果Fig.5 Calculation results of single member damage identification

3.3 多构件损伤识别

假定构件8,10,17均作为显著损伤构件(图4),每根构件的轴向刚度均折减50%。为了反映RFD方法的应用普适性,在本例中将3根损伤构件均设为环杆,损伤后结构的动力特性及其MPMRs计算结果如图6a所示。将有效模态选择的阈值设为10%,则共有4个模态被选中,包括模态9,19,21,22。与单构件损伤结构的计算相类似,对于每一个被筛选出的有效模态,在计算中考虑5%的随机噪声。随后对每一个输入的模态,计算结构的损伤系数rs值,并将计算结果正则化处理,如图6b所示。可知:模态9,19,21成功地识别出了构件8,10,17的显著损伤;但模态21的计算结果错误地识别了构件44的损坏;而模态22则没有成功识别出损伤构件。因此可以得出结论,模态9,19,21可以用于识别多个损伤构件,且对测量噪声稳定。所提出的RFD方法具有识别多个显著损伤构件的能力。

a—多构件损伤模型MPMRs; b—多构件损伤识别(模态9); c—多构件损伤识别(模态19); d—多构件损伤识别(模态21); e—多构件损伤识别(模态22); f—将损伤构件63作为附加约束的情况。图6 不同参数对构件损伤的影响Fig.6 Different parameters’ influence on member damage

3.4 损伤构件作为附加约束

实际情况中,严重损伤构件有可能是作为附加约束的构件。为了验证在这种情况下RFD方法对其他构件损伤的识别结果,假定构件25和63的轴向刚度折减50%,如图4所示。与此同时,根据构件重要性的计算结果,构件63同时也被设置为附加约束。选择模态8作为有效输入模态,采用与单个构件损伤识别相同的计算过程得到识别结果,如图6c所示。结果表明,计算结果成功地识别了构件25的显著损伤。因此,作为附加约束的构件损伤对其余构件损伤的识别没有显著不利影响。

4 结 论

本文提出了一种实用的RFD方法用于识别既有网壳结构中损伤构件的分布位置。根据网壳结构特点和模态残余力分解法,推导出一组多元线性方程组来计算结构构件的损伤系数。根据构件数量N和节点数量M的不同关系,讨论了3种计算过程的解决方案。针对无穷解的普遍情况,通过建立基于Ritz矢量敏感度分析的构件重要性分析方法,基于部分最不重要构件对结构刚度贡献很小的特点,将筛选出的部分不重要构件设定为完好无损,以此作为附加条件引入计算中,使方程组具有唯一解。

通过建立K6型网壳结构实例,验证了RFD方法的有效性,并得出以下结论:

1)分别讨论了单构件损伤和多构件损伤情况下的损伤识别,计算结果表明,RFD方法在两种条件下均成功识别出损伤构件。

2)讨论了将损坏构件作为附加约束的一种特殊情况。结果表明,作为附加约束的损伤构件不会影响其他受损构件的识别。

3)如果某个构件与损伤构件相邻,虽然可能会错误地将该构件识别为损伤构件,但仍能定位显著损伤构件的主要分布区域。另外,不同模态输入条件的识别结果也不同。为了消除错误的识别以及遗漏,有必要综合所有计算结果来分析判断最终识别结果。