空调烟机管路系统异响分析及优化
徐雪峰, 余丙松, 陈振雷*,, 李刚刚, 王 勇
(1.宁波大学 海运学院, 浙江 宁波 315211,E-mail:chenzhenlei@nbu.edu.cn;2.宁波方太厨具有限公司, 浙江 宁波 315336)
随着经济社会的发展,人们对生活品质的要求也越来越高,空调烟机便应运而生,其将空调的制冷功能和油烟机的抽油烟功能有机集成为一体,解决了用户夏季在厨房做饭环境闷热、大汗淋漓这一痛点问题,大大提升了厨房环境的舒适性。但由于机器内部有空调系统的存在,不可避免的会产生振动和噪声。由于空调配管的管壁薄,直径小,质量轻,支承简单,管道系统的刚度较低,质量分布不均匀,在工作时很容易产生强烈的振动,造成结构的损坏[1]。因此管道系统在空调结构中起着举足轻重的作用,是空调结构减振降噪的主要研究对象。
因此,大量学者针对空调管路系统的振动问题做了许多研究。文献[2-4]通过有限元法,在模态分析的基础上进行了随机振动分析, 计算出管路系统的疲劳寿命,提出了相应的管路优化方案。文献[5-8]利用有限元的方法对管路系统进行模态仿真计算,发现问题频率,进而对管路进行结构优化,使之与激励源的基频或倍频相错开,避免了共振的产生。张晓伟等人利用有限元法,对空调管路系统进行仿真计算,通过调整壁厚和配重和两个变量,有效的抑制了空调管路系统的噪音[9]。文献[10-12]采用模态实验和响应测试的方法获取了空调室外机管路的振动特性,同时利用有限元分析软件对管路振动特性进行研究,得到了管道的固有频率和振动响应,并采用增加阻尼块的方式减小了管道的振动。
本文针对空调烟机长时间停机以后再开机时,压缩机配管振动剧烈,产生短暂异响问题展开研究。首先进行了压缩机激励源振动测试和管路系统模态测试,排除了在正常工作状态下管路系统固有频率与压缩机基频或倍频相近而产生共振的问题。其次,在标定完成的有限元模型上计算管路系统所受内压对模态的变化规律。通过分析,在U型管存在积液内压不均情况下,管路系统1阶固有频率和激励源基频相近是管路产生共振和异响的原因。最后通过对管路结构重新设计,改变管路走向,避免积液的产生,消除共振和异响,并通过试验验证。
1 理论分析
1.1 模态分析理论
结构模态是由结构本身的特性与材料特性所决定的,与外载等条件无关。通过模态分析可以确定部件的固有频率和振型等[13]。对于一个具有多自由度的系统,运动微分方程为:
(1)
式中:M—质量矩阵;C—阻尼矩阵;K—刚度矩阵;x—位移矢量;f(t)—激励矢量。
在不计阻尼的情况下,式(1)对应的齐次方程可以简化为:
(K-ω2M){φ}=0
(2)
由式(2)可求得特征值ω2,ω为系统固有频率,ω对应的特征向量{φ}即为固有频率对应的振型,由ω=2πf(t)可求出结构的各阶固有频率及振型[14-15]。
1.2 控制方程
流体力学三大基本方程为连续性方程、能量方程和动量方程,即流体流动必须满足质量守恒定律、牛顿第二定律和动量守恒定律[16]。基于这些基本的物理原理,引入流体力学的湍流模型,构建出流体的运动模型。
(1) 连续性方程

(3)
式中:ρ为密度;t为时间;U=ui+vj+ωk,u,v,ω表示流速在x,y,z坐标方向的分量。
(2) 量方程
(4)
式中:P为流动压力,μ为流体动力黏度,SMx为流体源。
(3) 量方程
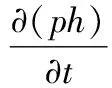
(5)
式中:λ为流体的导热系数,h为流体比焓,Sh微流体的内热源,φ为耗散函数。
(4)k-ε湍流模型方程
(6)
式中:μt为湍流粘度,Cμ为湍流粘性系数,k为紊流动能,ε为紊流动能耗散率。
2 振动测试与分析
2.1 压缩机激励源振动测试

▲图1 激励源振动测试测点布置
压缩机作为空调系统唯一激励源,因此需要对压缩机进行振动测试,找到压缩机的激励频率。本次测试采用的DH5922N动态信号测试分析系统对压缩机机进行振动测试( 采用三向传感器)。测点布置在压缩机缸体上,如图1所示。
压缩机经过多次振动数据的测试,测试结果基本一致,测点的X、Y、Z三个方向的加速度频谱如图2所示,3个方向产生振动峰值的频率一致,激励源压缩机的基频为50 Hz。

▲图2 激励源的振动加速度频域图
2.2 管路系统模态测试
模态测试是获取空调管路系统在正常状态下的固有频率和相应的振型一种有效方法。本次测试采用DH5922N动态测试仪、三向加速度传感器和模态冲击力锤对空调烟机中的管路系统进行模态测试。由于压缩机配管质量较轻,因此本次测试采用单点激励单点响应的测试方法,冲击力锤的锤击信号作为输入信号,三向加速度传感器采集的振动信号作为输出信号,实验模态测试将获得结构的频率响应函数,并由此求出其模态特性[17]。
管路系统模态测试结构布点图和现场测试安装照片如图3和如图4所示。

▲图3 管路系统模态测试结构的布点图

▲图4 管路系统模态测试现场图
对三组模态测试数据进行汇总整理,如表1所示,以三组数据的平均值作为正常状态下管路系统的前六阶固有频率。

表1 管路系统模态测试数据
由上述测试数据对比分析可见,正常状态下管路系统的前六阶固有频率与激励源基频或倍频不一致,因此正常工作状态下不会产生共振而出现异响。
3 模态分析
为了找出管路长时间停机再启动状态下振动过大、产生异响的原因,考虑U型管长时间停机后底部有积液,再启动后管路堵塞、单侧内压增加对管路固有频率的影响,需要进一步研究管路系统正常状态下和堵塞状态下的有限元模态分析。
3.1 管路系统正常状态下模态分析
3.1.1 有限元模型的建立
空调烟机的管路系统主要由压缩机、回气管、排气管、储液罐等组成。空调管路系统几何模型示意图如图5(a)所示。本研究压缩机配管,和压缩机缸体其厚度远小于另外两个维度方向尺寸,因此配管及缸体仿真模型选用壳单元网格进行处理。管路系统的有限元模型的节点总数为23 437,单元总数为11 695,单元尺寸范围在1 mm~5 mm。建立的空调烟机管路系统有限元模型如图5(b)所示。
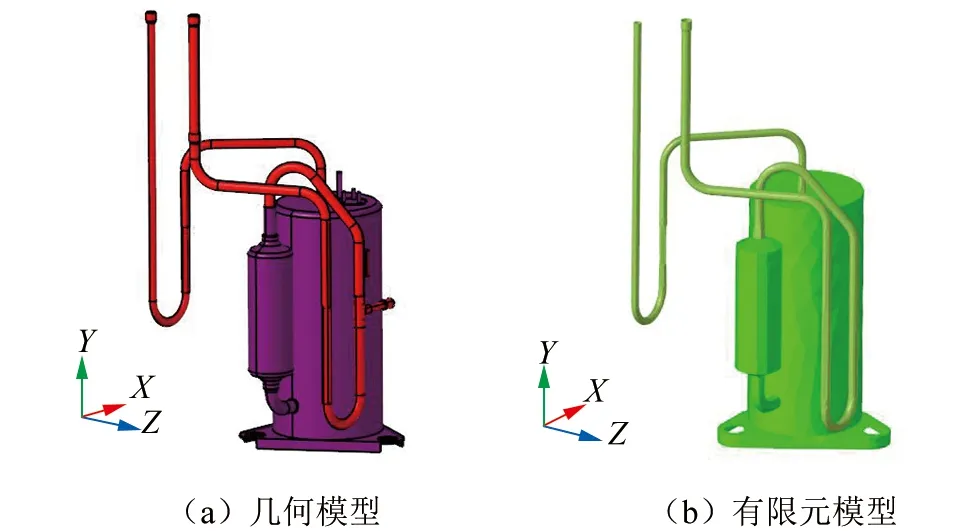
▲图5 空调烟机管路系统模型
3.1.2 材料参数和边界条件的设定
(1)空调烟机管路系统各部件材料特性
空调烟机管路系统各部分的材料属性如表2所示。
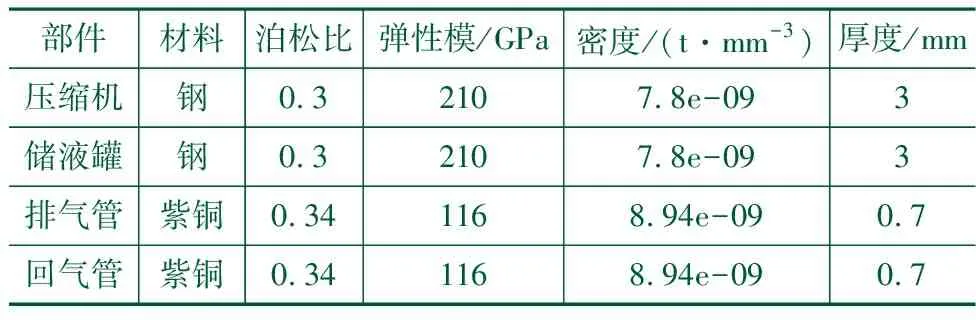
表2 管路系统各组成部分的材料属性
(2) 约束条件的设定

▲图6 弹簧约束假设
针对空调压缩机的实际运行状况,压缩机通过橡胶底座与底板钣金件相连,同时排气管和回气管分别与散热片、冷凝器相连,为了提高仿真计算的精度,假设弹簧约束处理,并根据实际测试情况分别确定三方向上的弹簧刚度。弹簧约束假设如图6所示。
3.1.3 管路系统仿真模型标定
在仿真模型初建完成后,根据测试数据,对初建模型进行边界条件的敏感性分析,最终确认排气管弹簧约束处X、Y、Z三方向的刚度分别为:13 500 N/mm、810 N/mm、810 N/mm;回气管弹簧约束处三方向的刚度分别为:11 100 N/mm、667 N/mm、667 N/mm;压缩机脚垫弹簧约束处三方向刚度分别为800 N/mm、800 N/mm、800 N/mm,计算该管路系统的仿真模态,完成与测试模态的标定。图7为管路系统前二阶约束模态云图。
管路系统正常状态下模态有限元结果与测试结果的误差对比如表3所示。由表3可知,测试结果与仿真结果相比较,各阶模态固有频率的最大误差均在10%以内,说明此有限元模型能够较准确地模拟管路的实际结构。

表3 正常状态管路系统模态有限元结果与测试结果的误差

▲图7 管路系统前二阶约束模态云图
3.2 管路系统堵塞状态下模态分析
为了找出异响原因,假设U型管有积液存在,计算管路制冷剂受堵状态下内压计算,并将此内压加载到受载管路的模态仿真计算中,寻找空调烟机长时间停机后再开机时产生短暂异响的原因。
3.2.1 堵塞状态下管路内压计算
(1) 流体域建模
考虑U型管存在积液,对排气管路进行CFD数值模拟,气相和液相的冷媒同时存在于管路中,不考虑相变过程。为了使模型在迭代计算中有较好的收敛性,在模型中建立了边界层。气相制冷剂R22材料属性设置为:密度ρ=0.085 g/cm3、动力粘性参数v=1.418×10-5kg/(m·s)。液相制冷剂R22材料属性设置为:密度ρ=1.082 g/cm3、动力粘性参数v=1.231×104kg/(m·s),流体域模型如图8所示。

▲图8 流体域模型

▲图9 固体域和流体域网格图
(2) 管路及流体域网格划分
空调管路是一个光滑的曲管结构,考虑管路的流固耦合作用,所以网格划分包括固体域和流体域网格,并且在两域的交界处,建立流固耦合面(Fluid Solid Interface),这样流体和固体之间的载荷能够在流固耦合面上进行传递[18]。流体单元为R22,固体单元为铜管。其中流体域共包含159 581个节点和30 200个单元,固体域共包含70 320个节点和11 534个单元。固体域和流体域网格图如图9所示。
(3) 管路及流体域的边界条件
计算管路在单向流固耦合作用下的流体仿真时,压力的求解是瞬态条件下的求解,根据工程实际,设置其进口压力为2.06 MPa,出口压力为1 MPa。湍流模型的选择为标准k-ε模型,假设排气管路U型管处的积液量为10 mm、20 mm、30 mm高三种情况,分别进行CFD数值模拟,求得其最大冲破积液瞬间的压力值。
(4) 堵塞状态下管路内压计算结果与分析
通过Fluent计算,分别得到了积液量为10 mm、20 mm、30 mm高三种情况冲破瞬间的流场云图,如图10所示。由流场计算结果可知,当U型管处积液量分别为(10、20、30)mm高时,最大冲破压力分别对应为(2.831、3.352、4.463)MPa。

▲图10 三种工况流场计算结果图
3.2.2 管路系统受载状态下模态分析
表4为不同积液高度下管路单侧受载对应的3种工况(其中工况4、5为无积液工况),计算管路系统不同受载情况下固有频率。表5为上述工况及上节已对标完成的管路系统正常工作状态下模态分析结果。

表4 空调烟机仿真管路堵塞和畅通模态计算工况
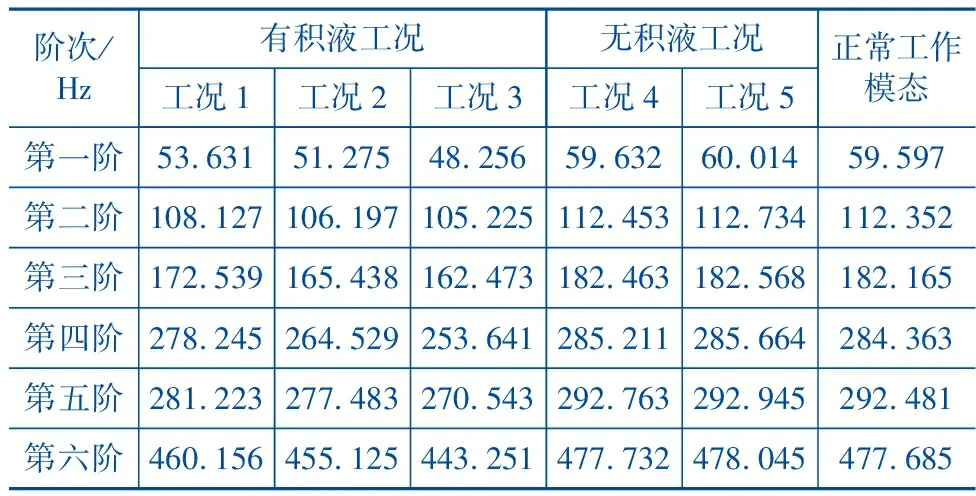
表5 管路系统不同工况下的固有频率值
对表中数据分析可知:当管路整段加压相同时,管路系统各阶固有频率与其正常工作状态下模态相比,略有增加,但变化很小,原因是均匀内压下对其系统刚度有少许增加。当考虑U型管处有积液存在,排气管U型管两侧所受压力不同时,其各阶固有频率值与正常工作模态相比,会有较大减少。原因是不均匀管路压力作用下导致管路系统刚度改变不均。其中模拟积液存在的前三个工况,管路系统第一阶固有频率从59.957 Hz分别下降至(53.631、51.275、48.256)Hz,与激励源压缩机基频50 Hz较为接近。
4 管路系统异响优化分析
4.1 优化设计及仿真结果
通过仿真计算,验证了积液的存在导致空调烟机长时间停机再开机时有异响产生这一假设。以下通过对管路结构重新设计,改变管路走向,避免积液的产生。具体的结构改变如图11所示。
以已建立的管路系统模态分析流程和边界条件,对上述管路系统优化方案进行模态分析验证。图12为优化后管路系统的前二阶模态云图,表6为管路系统优化后前六阶固有频率值。

表6 优化后管路系统的前六阶固有频率

▲图11 管路系统的优化方案

▲图12 优化后管路系统的前二阶模态云图
由表6可知,优化后的管路系统,通过改变排气管结构走向,避免停机状态下有积液的产生,并通过模态仿真计算验证,其前六阶固有频率成功避开了激励源压缩机的基频和倍频,避免共振的产生,消除了异响。
4.2 试验验证
根据管路系统的优化方案对该空调烟机管路系统进行优化改进,改进以后空调烟机在长时间停机以后再开机时无异响。此外,还对改进以后的管路系统进行了模态试验,表7为仿真结果和测试结果对比分析。由表可见,各阶模态固有频率的最大差别均在10%以内,说明仿真模型相对精确,再一次验证了优化后管路系统前六阶固有频率与激励源压缩机基频或倍频无重合和相近,避免共振的产生,消除了异响。

表7 优化后管路系统的仿真值和模态测试值误差对比
5 总结
本文以某空调烟机为例,通过管路异响分析对其进行分析优化,建立一套集理论分析、仿真模拟及试验测试的民用机械减振降噪分析流程,为后续同类产品消除异响提供有益的参考。主要结论如下:
(1) 管路正常工作状态下,管路系统前六阶模态和激励源基频及倍频并不重合和相近。
(2) 当管路整段加压相同时,管路系统各阶固有频率值与其正常工作状态下模态相比,会有微量的提升,但变化很小;在U型管积液单侧内压较大,管路系统各阶固有频率值与其正常工作状态下模态相比,会有较为明显的下降,管路1阶固有频率和激励源基频相近是管路产生共振和异响的原因。
(3) 通过改变排气管管路结构,进行优化,避免了积液的产生,同时使该设计的管路系统前六阶固有频率与激励源压缩机基频及倍频相错,试验测试验证了上述改进设计的有效性。

