面向区域化综合能源调度的负荷预测算法设计

苗福丰，吴豫

（国网河南省电力公司，河南郑州 450052）

能源是保障国家经济发展和人民生活的命脉。多年来，人类的发展均依靠传统的化石能源，而随着化石能源枯竭与各种新能源技术的发展，世界能源结构将出现重大变革[1-4]。2020 年，我国提出了“碳中和”及“碳达峰”的双碳目标，这意味着清洁能源将逐渐占据能源消费的主导地位。“十四五”是我国实现“双碳”目标的关键窗口期，故深入开展多种能源协作的综合能源系统研究，并提高清洁能源消费占比与化石能源利用率，对于降低碳排放均具有积极的意义。在此背景下，小范围、区域化的综合能源系统将扮演更为重要的角色[5-13]。但目前，综合能源系统的应用仍存在诸多亟待解决的问题，其中之一便是综合能源系统内的风能、太阳能等一次能源的供应具有波动性及随机性。因此，只有精确实现区域内的负荷预测才能实现各种能源形式的有机调度。

近年来，随着人工智能技术的发展，将负荷预测问题转化为时间序列的处理问题，再借助神经网络（Back Propagation，BP）、支持向量机（Support Vecor Machine，SVM）与小波分析等方法来进行数学分析，成为了解决能源负荷预测的主要思路[14]。该文针对某区域的综合能源系统建立了调度模型，然后在时间序列分析的基础上引入了循环神经网络中的Seq2Seq（Sequence to Sequence）模型，实现了对负荷的预测。

1 理论基础

1.1 综合能源系统调度模型

区域综合能源系统，是“双碳”背景下的基础供电单元。在该系统中存在多个能源源头，且不同能源形式互相耦合。对于综合能源系统的调度，与传统的电力系统有较大区别。在满足安全、平稳供电的前提下，综合能源系统还需最大程度地降低运行成本及提升清洁能源占比。文中的区域综合能源系统组成结构[15]如图1 所示。

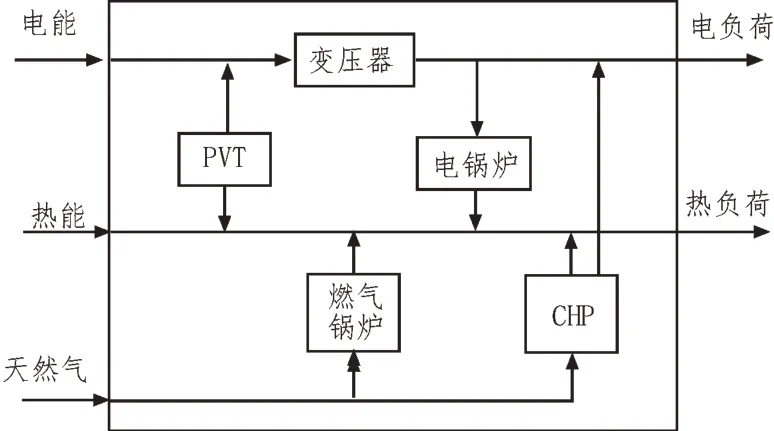
图1 区域综合能源系统结构图

将区域能源的综合调度问题进行抽象，能够转化为数学中的非线性规划问题。记F为图1 系统的运行成本，则该问题的目标函数可写作：

其中，Ek、Gk、Pk、Lk分别是购电成本、天然气成本、设备维护成本、设备启停成本，且各自的计算方式如下：

其中，ζ、λ分别是各自的归一化适应度，w是个体位置，P、F、L为相应的成本计算核函数，T为总的运行时间。

根据非线性规划模型的定义，需找到实现函数目标的约束条件。对于区域综合能源系统，首先变压器Ti、输电线路Pe、电锅炉Pb、燃气锅炉TF等功率器件要满足其功率限制：

其次，系统内的天然气输入Gin满足其上下界与天燃气管网Gfmn的压力约束：

1.2 区域内负荷的短期事件预测算法

功率负荷是区域内能源综合调度的唯一依据，因此在进行能源调度前需对调度时刻的能源负荷大小进行预测。短期的负荷预测精度与预测时所使用的算法相关联，所以为了提升预测精度，该文提出了一种基于时间序列及Seq2Seq 网络的预测算法[16-18]。

Seq2Seq 是一种特殊的循环神经网络（Recurrent Neural Networks，RNN）。传统的神经网络中，不同元素间相互独立，而信号通过全连接的方式在输入层、隐藏层及输出层之间相互传递，且同一层节点间没有信号传递。但在处理时间序列问题时，不同时间节点之间的数据是有关联的，因此传统的神经网络不再适用。在此种场景下，通常使用图2 所示的循环神经网络。

图2 RNN网络结构示意图

从图2 中可以看出，RNN 网络同样包括输入层x、隐藏层h、输出层y，且不同的隐藏层之间相互连接。对于t时刻隐藏层的状态ht，有：

t时刻的输出yt为：

其中，U、W、V是网络中信号传递使用的共享参数，f、g分别为隐藏层与输出层的激活函数。

从图2 中还能看出，在经典的RNN 结构中，输入及输出的序列维度是相同的，这与该文的应用场景不符。因此，文中引入了Seq2Seq 循环神经网络，该网络的基本结构如图3 所示。

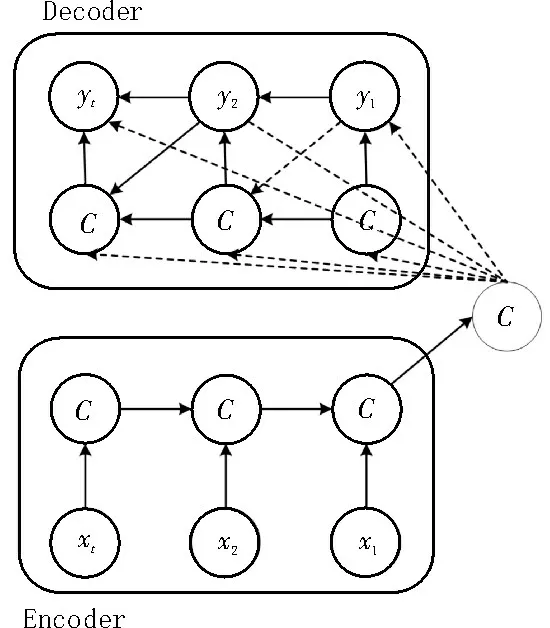
图3 Seq2Seq结构示意图

Seq2Seq 由编码器Encoder 和解码器Decoder 组成。在t时刻，Seq2Seq 将输入序列X={x1，x2，…，xm}，依次输入编码器的输入端，通过编码器中预置的非线性变换单元得到中间向量并存储在c中。随后，解码器利用c中的信息与t-1、t-2、…、t-N前N个时刻的输出值得到输出yt，Seq2Seq 模型的数学表达如下：

从式（10）可以看出，通过引入编解码器实现了输入输出序列的可变，从而保证了RNN 网络在电力负荷预测场景中的可用性。编码器的非线性变换函数可根据RNN 网络的应用场景进行选择，该文使用的是GRU（Gate Recurrent Unit）函数。GRU 中包含了更新门r、输出门h及输入门z共3 个门，其信号的流转过程如下：

2 方法实现

2.1 实验设计

在上文中，首先将区域综合能源系统的能源调度问题转换为数学中的非线性规划问题，并给出了待调度区域的数学模型。随后，针对该区域的能源调度研究了负荷预测的方法，并引入了一种基于Seq2Seq 网络的循环网络算法。接下来将对预测算法的精度及其在区域内能源调度中的可用性进行验证。表1 给出了图1 区域综合能源各个能源节点的硬件配置情况。

表1 能源节点的配置情况

在评估负荷预测算法的精度时，使用平均绝对误差（Mean Absolute Deviation，MAE）和均方根误差（Root Mean Squard Error，RMSE）作为评价模型调度精度的指标。其中，MAE 能够抵消正负误差。而RMSE 则可描述预测结果的波动性，两个指标的计算方法如下：

为训练Seq2Seq 网络，对图1 所示的能源系统进行了数据采集。采集的时间为1 年，时间粒度为15 min/次，故对于气温、负荷数据每天可采集到96个样本点。根据电力负荷的周期特性，设计了表2所示的网络输入特征。其中，日、周和月正余弦周期序列的特征构造方法如下：

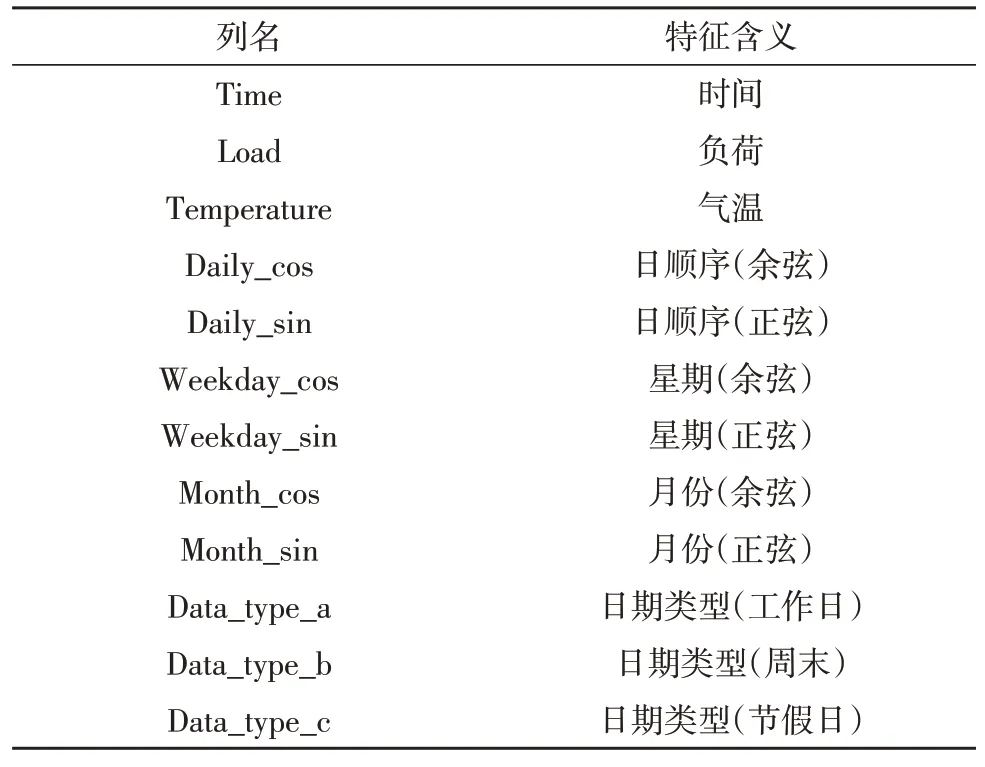
表2 负荷预测算法构造的特征序列

其中，日、周、月的T、m取值如表3 所示。

表3 正余弦周期序列的取值表

表4、5 分别给出了负荷预测方法仿真时，所需的软硬件及算法的仿真参数。

表4 算法仿真的软硬件环境

表5 算法仿真参数

2.2 实验结果

为了实现对图1 区域能源的调度，首先要实现对电力负荷的精准预测。图4为该文设计算法针对数据集中某日电负荷预测的结果。从图中可以看出，预测值及实际值样本点基本重合，且曲线走向一致。

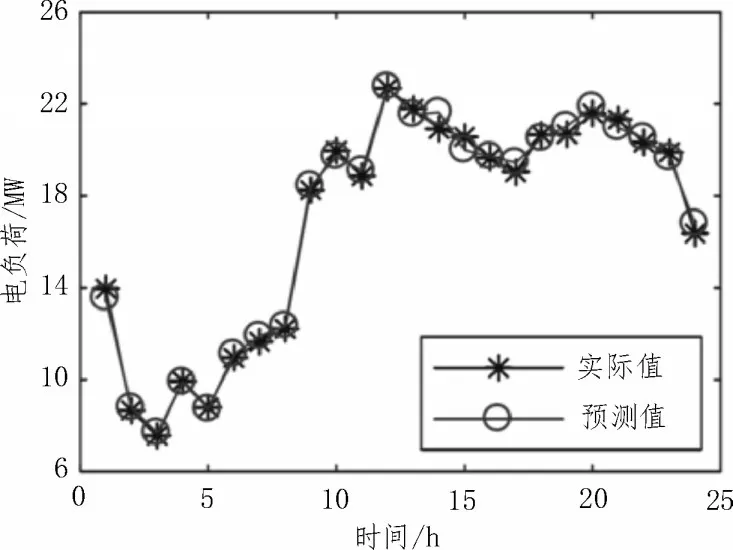
图4 算法预测曲线

为衡量该文算法的预测精度，表6 给出了图4 中样本点的计算结果。可以看出，该算法的预测精度较高，对于负荷预测结果的相对误差均在4.5%以内，能够作为该区域内能源调度的依据。此外，还引入了BP 神经网络和普通RNN 网络进行对比，3 种算法的MAE、RMSE 计算指标如表7 所示。

表6 算法预测数据表

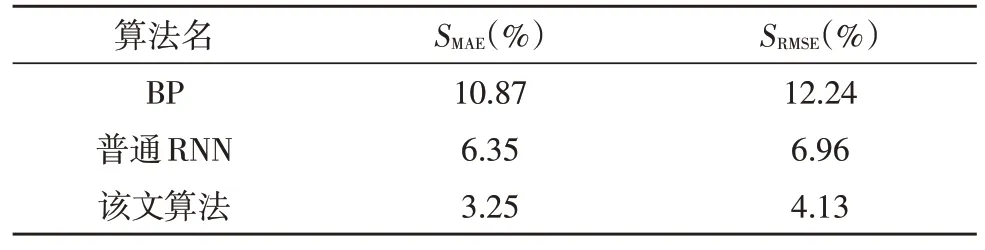
表7 不同算法的预测指标结果

从表7 可以看出，普通RNN 算法的MAE、RMSE较BP 神经网络算法分别提升了4.52%、5.28%，说明了循环神经网络更适合于时间序列的处理问题。而该文算法相较于普通的RNN 网络在MAE 与RMSE上分别提升了3.10%、2.83%，证明了Seq2Seq 模型对于不同输出长度的时间序列处理具有更优的性能。同时基于Seq2Seq 模型的预测结果，文中对当日的能源调度进行了仿真，计算机的计算耗时为2.442 s，且当日的调度总成本为60.231 万元。

3 结束语

随着我国能源消费形式的变革，区域化的综合能源系统将逐渐在“双碳”战略中扮演更重要的角色。为了提升综合能源系统的调度水平，文中重点研究了能源负荷的预测方法，且设计的基于Seq2Seq网络模型能够连接维度不同的输入输出向量。仿真结果证明，其相较于传统的BP 网络及RNN 网络具有更高的预测精度，故可应用于综合能源调度的生产环境中。