基于配网评价指标和聚类分析的电网区域划分算法

陈晓彬，王学力，陈 波，陈 靖，黄觉慧

（1.国网福建省电力有限公司福州供电公司，福建福州 350000；2.广西中宇工程咨询有限公司，广西南宁 530007）

如何对配电网区域进行科学划分，始终是学界的研究热点。合理、科学的划分方案能够为电网远期规划提供发展方向、满足区域电网的经济发展及提高电网的运行经济性[1-3]。线路的供电半径和截面半径均会影响电网区域的划分，因此在实现电网划分之前，需要对分区方案进行科学地评估与归类[4]。传统的电网评价体系大多依赖于经验对单一指标分类，分类方案不够精细，导致其无法满足现有电网发展的要求[5]。文献[6-7]基于图论方法（Graph Theory）将负荷节点作为物理分割点，但该方法依赖于阈值的选取，若阈值取值过小，便会导致划分区域过大而无法达到分区目的。文献[8]则采用分级分类法，通过供电半径的大小将电网分为不同的区域。文献[9]通过合并距离较近的负荷节点，应用最大最小距离方法（Max-Min-diatance）形成初始分区结果。但其在处理PV 节点时过于粗糙，导致分区结果的合理性有待进一步商榷。文献[10]改进了传统的聚类方法，弥补了电压控制分区存在容错率较低的情况，并通过计算电气距离得到无功源节点的分区方案。该方案不易受电力系统运行方式的影响，但较为依赖电网的拓扑参数。

该文基于聚类分析方法建立了电网区域划分评价体系，提出了基于配网评价指标和聚类分析的电网区域划分算法，该方法可将电气数据聚类分析以建立模糊相似矩阵，通过对电网的潮流计算及短路分析，建立区域配网中各个节点间的相似矩阵；同时基于传递闭包法求取动态聚类图，并根据电网的物理特性将其划分为合理区域。实际算例结果验证了该文算法的可行性。

1 评价指标与聚类分析

在聚类分析方法中，聚类是指将表示相似意义的组或类划分为同一类。而从本质上讲，聚类即为某个目标函数的最优解，通过相似性表征数据的紧密程度[11-13]。假设U为集合，k表示所属类别的个数，则类Ct需满足条件：

聚类分析的主要过程包括数据预处理、聚类及结果评价等步骤。其中，数据的聚类过程还包括数据准备、特征选取、特征提取与测试评估等步骤。

传统聚类分析的数据预处理步骤，可以作为数据库技术的重要环节。但是在实际的工程应用过程中，海量数据具有多维性，且容易受外界环境的影响。文中结合滑动窗口算法（Sliding Window Algorithm）对异常数据进行预处理，以改进传统算法精度较低的问题。异常数据剔除的主要作用在于剔除对应时间点的数据，并还原数据的真实性，直至满足置信限度。常用的错误剔除法为拉依达法，其基本思想：若测量值与平均值之差超过预期值的3 倍，则认为该数据在误差内为异常值，应将其剔除，且该方法操作简单、使用便利。在剔除异常数据之后，需对数据进行降低维度操作。首先需要观察数据趋势，分析时间与测量数据点，求出滑动窗口的多项式系数，并根据公式得到各个系数，具体如下：

式中，t为数据样本，a为滑动窗口的多项式系数，x为求得的相应维数所对应系数向量，j表示各个维度的维数，据此可得到矩阵的特征向量为：

在求特征值时，可根据数据流的维度确定特征向量矩阵。若矩阵中的行数等于列数，则采集到的数据条数相等，并可根据公式求得特征向量矩阵；若矩阵的行数不等于列数，则需根据奇异值分解方法（Singular Value Decomposition，SVD）将矩阵进行分解，再实现对特征向量的求解。

在聚类分析方法中，常用两个物理量之间的距离来表示两个变量间的真实距离，其距离可表示为：

式中，xi、yi表示样本X、Y中第i变量值，二者间的距离用差的平方和表示。

配网聚类分析的具体步骤如下：

步骤1：将采集到的数据进行标准化处理。假设配网区域U={x1,x2,…,xn}为具体的分类对象集合，评价指标个数为m，则每个分类对象可表示为：

由此即可得到原始矩阵X。

然后对数据进行标准化处理，根据模糊矩阵的原理，将所有数据均化成0～1 之间的数值，并选用平移标准差加以处理，则：

步骤2：按照聚类方法建立模糊相似矩阵，再由灵敏矩阵计算得到电气距离矩阵，从而建立起区域配网中各个节点之间的联系，并以此得到相似矩阵。

步骤3：基于传递闭包法求取动态聚类图，即将相似矩阵R转换为模糊等价矩阵R*。假设R为模糊相似矩阵，则必然有自然数d，使得R*为等价矩阵。假设λ为阈值，对其进行聚类，将相同水平上的数据归为同一个类型，形成动态聚类图。

为充分考虑区域内配网的发展水平，同时兼顾经济性，对主要指标进行分析：

1）配网“N-1”通过率，该指标主要指额定容量与最大负荷的比值；

2）供电模式比例，典型的供电模式有8 种，其计算公式为：

3）主变重载比例，该指标指变压器重载台数占总数的比例，其计算公式如下：

4）容载比，该指标为变电站额定容量与最大负荷的比值，其计算公式如下：

5）户均配变容量，如下：

6）综合电压合格率。

做到统筹配电系统发展现状，同时兼顾配电系统的运行经济性，将效果类指标与主要特性指标统一进行分析。

选取的评价指标能够有效反映配网能效水平，但是体现的量纲不一致，故需进行极致化无量纲处理。

2 电网区域划分方法

电网区域划分的方案较多，最简单的为根据所属地域进行划分，但该方法过于粗糙，不利于电力系统的分析与控制。而采用聚类分析的方法划分电网区域，可有效根据电网的物理特性将其划分为合理的区块，以便于进行潮流计算及短路分析[14-19]。具体的实施步骤为：1）输入电力系统的原始参数，包括支路阻抗、对地导纳、节点电压与无功补偿容量等；2）依据输入的原始参数进行潮流计算，得到灵敏度矩阵S；3）获取电气距离矩阵D；4）通过数据归一化将上述数据进行标准化处理，得到模糊矩阵；5）采用传递闭包法得到动态聚类图；6）进行初始分区；7）去除孤立节点，将其并入到电气耦合性最强的区域；8）将与多个PQ 相连的节点合并至PV 节点；9）检查结果，判断功率平衡条件，进而得到分区结果。基于聚类分析的电网区域划分流程如图1 所示。

图1 电网区域划分流程

为保证电网区域划分的合理性，需根据电网运行数据建立分层分区域数学模型，通过层次分析法（Analytic Hierarchy Process，AHP）检验区域电网的稳定性[16-19]。构建层次分析模型的核心是建立精准的评价矩阵，其主要思路是比较前后两个划分方案间的联系紧密度，若将两个划分方案的重要程度简化为0～1之间的任一数值，则评价矩阵可表示为：

式中，ann表示两个元素的重要程度。建立评价矩阵A后，可得到权重值，再计算评价矩阵的最大特征值，并进行一致性检验。一致性检验的计算公式为：

式中，λmax为最大特征值，n为评价矩阵的阶数。当C.I.=0 时，表示电网区域划分前后运行的参数完全一致。

当在电网区域划分过程中出现误差时，需引进修正系数（Correction Coefficient），并通过该系数对评价矩阵进行适当的调整，直至修正系数的值大于3。修正系数的表达式为：

以电网划分后的运行经济性为目标对电网进行评价，并以电压稳定性和运行经济性作为目标函数，综合考虑各个设备的成本问题，构建Well-being 模型，其架构如图2 所示。

图2 Well-being模型构架

3 算例分析

为验证该文所述方法的可行性，选择某区域配电网在多项指标下进行科学、合理地分类。首先收集该区域电网的发电机节点、负荷节点、无功补偿节点及支路的个数，利用公式计算得到灵敏矩阵与电气距离矩阵。然后将不规范的数据进行标准化处理，并基于模糊等价关系进行聚类分析，以得到动态聚类图。具体的配电网区域分类流程如图3 所示。

图3 电网区域划分流程

在电网正常运行情况下，根据前文得到的负荷节点的灵敏度矩阵如表1 所示。

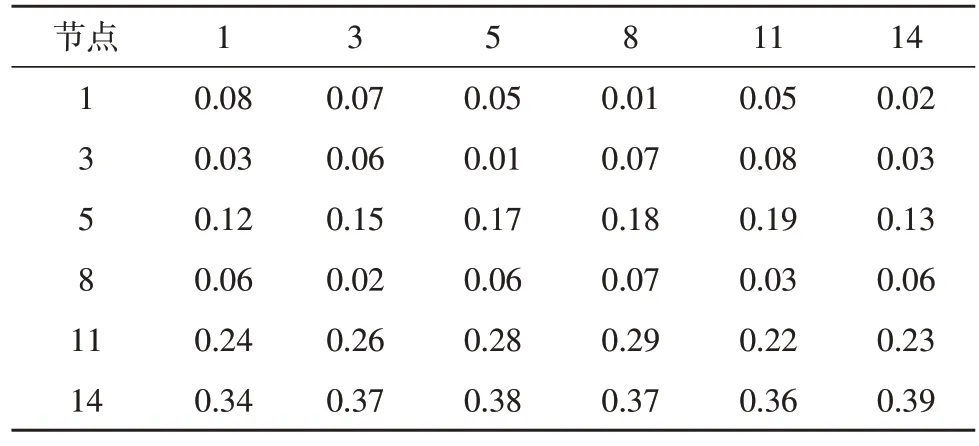
表1 负荷节点灵敏度矩阵

根据表1 的计算结果，进一步得到各个负荷节点间的电气距离如表2 所示。由此可分别计算得到各个节点对应的权矩阵、度矩阵及二者的特征值向量。

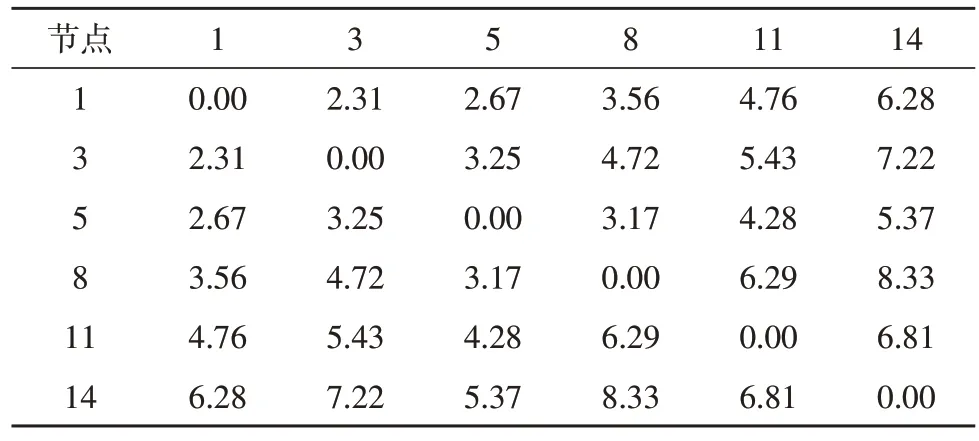
表2 负荷节点电气距离

运用综合权重算法得到每一类的基层各个指标权重，将各单项指标进行归一化处理，获得各个区域的综合得分如表3 所示，然后再进行聚类分析。需要注意的是表1-3 的数值均为无量纲数值。

表3 各个区域的综合得分

根据上述数据，可分析出该区域电网的关键节点为3、8、14，综合考虑各关键节点所在的区域，可进行无功电压控制，从而改善整个区域电网的稳定性。因此，能够得到该区域的电网重新划分情况如表4 所示，与原先的4 个区域不同，新划分的6 个区域中的部分节点间并不连通，原因在于该区域电网的划分主要是根据电气距离进行聚类划分，故区域间存在不连通的现象是合理的；此外，基于阻抗矩阵得到局部电压稳定指标，虽然阻抗矩阵理论上是满矩阵，但在实际计算过程中，电压灵敏度的导纳矩阵为稀疏矩阵，所以会出现孤立节点的情况。

表4 电网区域重新划分结果

4 结束语

现有电网区域划分方法通常会导致各区域间不协调、规划不合理的问题，与传统的常规方法不同，该文基于海量数据建立聚类评价体系，通过将数据归类，建立了模糊相似矩阵。通过传递闭包法求取动态聚类图，根据电网的物理特性可将该区域电网划分为电气特性相似、易于规划的不同区域。基于某区域配电网的历史数据样本对所提方法进行了案例测试与分析，科学地将该区域电网划分为不同的类别，为配电网的发展提供了可靠的数据支撑，有利于配电网规划工作的顺利开展。