基于深度学习与数据挖掘的在线学习预测评估模型设计
刘 静,由志勋
(1.西安工程大学,陕西西安 710048;2.西安热工研究院有限公司,陕西西安 710000)
近年来,随着“互联网+”概念的不断发展,数字化教学对教育,尤其是高等教育产生了重要影响。而各领域的网课层出不穷,为人们的学习提供了新方式[1-4]。自新冠肺炎疫情爆发以来,全国各大高校相继调整了返校时间。而为保证大学生们的学习进度,教育部提出了“停课不停学”的行动计划,这一计划也引发了社会各界对互联网在线课程资源的关注[5-7]。
互联网在线课程在我国已有十余年的发展历史,在这期间辍学率和流失率是该课程所面临的主要问题[8]。使用网络教学中的学生行为数据,来预测学生的学习效果并进行精准教学干预,已成为当前相关学者研究的热门课题之一[9-10]。上述相关文献均已实现并取得了一定的效果。但在影响因素方面,仍未能给出影响学习效果的关键指标,且在评估各个指标的影响时,定性与定量的评估相交杂,故主观因素影响较大。
文中采用智能化的深度学习技术,对学习成绩实现预测,且构建了学习效果评估模型。利用数据挖掘技术对可能影响成绩的各种因素进行聚类分析,并总结出了关键指标。在分析各个关键指标的影响权重与成绩预测时,采用梯度渐进回归树构建预测模型,从而实现成绩预测。
1 成绩预测评估模型框架
网络课程这种全新的教学方法与学习体验,对教师和学生而言均是一种挑战。如何根据学生在网课上的交互行为及相关数据来预测学习效果,并对学生的学习状态进行评估与干预,成为该文研究的重点[11-12]。
文中所提出的高校学生成绩预测评估模型可分为两个部分:一是总结出影响学生成绩的关键因素、指标;二是对学生成绩进行预测和评估,具体如图1所示[13-14]。根据预设的变量,利用聚类分析法,从学生网课的平时考核成绩、学习行为归类出影响学生成绩的关键因素以及各个因素的影响权重,进而构建成绩影响因素体系,将其作为成绩预测模型的输入信息与初始参数;再使用深度学习中的梯度渐进回归树算法深度挖掘数据背后的逻辑,并对初始参数进行修正。当预测结果与实际成绩的差异低于阈值时,制定提高学习成绩的干预措施;而当预测结果与实际成绩的差异大于阈值时,则筛选变量,且重新构建成绩影响因素体系。
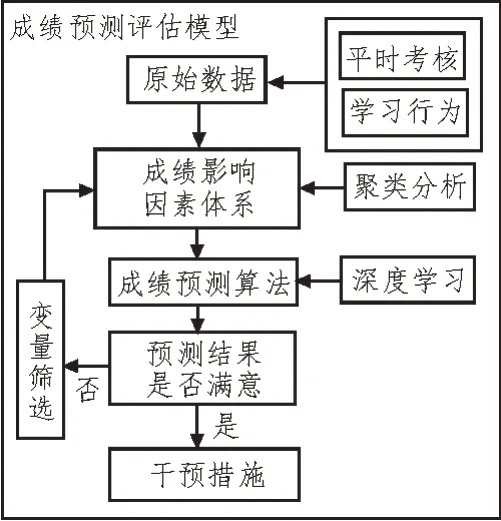
图1 成绩预测评估模型框架示意图
2 成绩预测评估模型
2.1 成绩影响因子体系构建
学习成绩预测与评估模型的构建需要明确关键影响因素的个数和权重,在此过程中使用的数据主要分为学生的平时考核成绩与在线学习行为。平时考核成绩为定量数据,仅需对数据是否重复、缺失进行检查后,便可进行聚类分析;而学习行为则是定性数据,需要将其通过编码转换为定量数据。文中所研究的学习行为数据分为以下几类,如表1 所示。
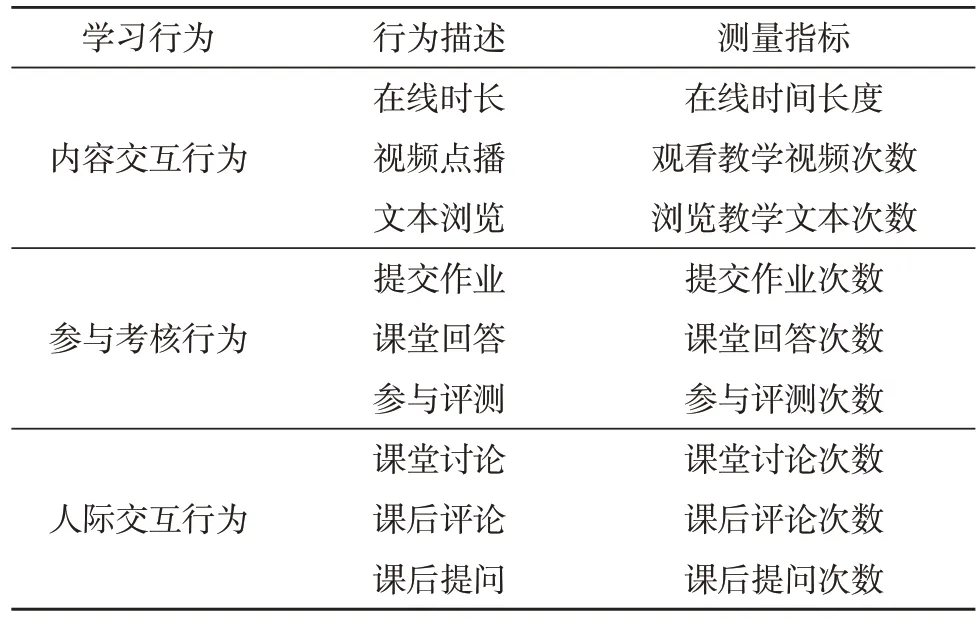
表1 学习行为数据
通过平时考核成绩能够直观地了解学生的学习效果,而学习行为则比较抽象,故文中使用数据挖掘中的K-means 算法来挖掘各类学习行为与学习成绩之间的关系[15],以明确关键影响因素,并提高学习成绩预测的准确率。
该文所采用的K-means 算法,又被称为K-均值算法[16],其设计的核心思想:预设聚类的个数,依据事先设定的规则,持续将在距离种子点一定范围内的个体划分成指定簇;再通过迭代更新的方式,事先指定簇的划分个数。在每次迭代过程中,选用的参考点为上一次迭代簇的质心。具体的算法流程如图2所示。

图2 K-means算法流程图
从图2 可以看出,K-means 算法的终止条件是算法收敛。因此文中采用畸变函数来判断算法是否收敛,具体表达式如下:
式中,J函数表示各个个体到达质心的距离平方和。当J函数为最小值时,代表K-means 算法收敛,即质心μi和类别ci分别收敛。当J函数不是最小值时,通过固定每个簇质心μi或类别ci,调整另一个变量,直至J函数为最小值。
2.2 基于梯度渐进回归树的预测模型
在筛选出关键影响因素后,再使用深度学习中的梯度渐进回归树来分析关键影响因素与成绩之间的联系。梯度渐进回归树是一种以决策树为基础的Boosting 算法,其本质为新生成的树均通过父代树的残差来进行学习,且利用损失函数的负梯度作为整个算法残差的近似值,并拟合成一棵回归树。故最终的预测结果为所有回归树预测结果的叠加。具体过程如下所示:
设定成绩预测的数据集为D={(x1,y1),(x2,y2),…,(xn,yn)},损失函数被定义为L(y,f(x)),回归树的最大深度数值为S。
1)依据式(2)预设常数因子c,使得损失函数最小。
2)以迭代的方式建立M棵回归树,对于每一个样本数据,均利用式(3)计算损失函数的负梯度在回归树的数值,作为残差的初始估计值。
同时将{xi,rmi}用回归树拟合,以得到第m棵回归树h(xi,λm),回归树中λm为模型参数。
3)损失函数的最小化由模型参数权重得到βm,并使用线性搜索来计算权重βm:
4)在得到βm之后,利用更新步长α将模型更新如下:
5)完成所有迭代次数后,即可输出最终模型:
在内容交互行为中,在线时长t是以分钟为单位进行统计的。为避免因数据单位不一致而导致预测结果的差异性,需要将在线时长数据进行归一化处理,得到分布在[-1,1]之间的数据:
由上述分析可知,梯度渐进回归树模型的建立需要3 个参数:回归树数量M、每棵回归树的最大深度S和更新步长α,且回归树的数量决定了迭代次数。为防止模型训练时出现过拟合现象,每棵回归树的最大深度初始值为一个较小的数值。更新步长的大小决定着模型收敛速度的快慢。文中采用参数枚举的方式来选定M、S、α这3 个参数,并以交叉验证的方式对其进行考核,考核评分高的组合作为最终模型参数的数值。考核标准为拟合优度,如式(8):
式中,R2代表拟合优度,m为样本个数,Yi为样本实际数值,yi为样本预测值。而y′为预测平均值,该值越趋近于1,则表示拟合效果越好。
参数枚举优化过程如下:
1)初始化参数M、S、α,M=[M1,M2,…,MK1],S=[S1,S2,…,SK2],α=[α1,α2,…,αK3],参数枚举数量分别为K1、K2、K3。
2)将样本数据分为n份进行交叉验证。选择任意一组样本数据作为目标集合,利用其余的样本数据对步骤1)中的某一组参数进行优化训练与计算拟合优度,并将平均拟合优度作为该组参数的最终评估结果。重复此操作,直至每一组样本数据均可作为目标集。
3)选择步骤1)中的另一组参数组合,进行步骤2)的操作,直至所有的参数组合均得到平均拟合优度。
4)比较各个参数组合的平均拟合优度数值大小,且将最高数值对应的参数组合定为模型的最终参数。
3 测试与验证
为了测试文中所提成绩预测评估模型的性能,选取了某所高校共计2 358 名大学生的网络课程学习数据,且该数据分为70%的毕业生数据与30%的在校生数据。毕业生数据被用来训练成绩预测评估模型的参数;而在校生的学习数据则用来验证模型的有效性。在进行模型训练前,使用Notepad++工具及R 语言对原始数据进行预处理:清除重复、无效的数据并对各类数据进行归一化处理。通过K-means聚类算法得到关键影响因素后,再将这些因素作为梯度渐进回归树模型的输入。文中采用枚举的形式,对训练样本进行交叉验证。
文中使用Matlab2016仿真软件平台作为模型训练的软件环境,硬件环境配置了64 bit、32 GB内存与1 TB机械硬盘以满足高速、海量的模型训练计算资源需求。
在模型训练前,依据经验设定K-means 算法的聚类个数及梯度渐进回归树模型各个参数的范围。为了筛选出影响成绩的关键因素,各簇之间的相似程度应较低,而簇内的个体相似程度则较高。将K值的初始范围设定为[3,6],并根据不同的K值,计算各个个体到相应质心的均值距离,结果如表2 所示。

表2 不同K值下个体到质心的均值距离
从表2 可以看出,当K值为5 时,各个体到质心的均值距离最小。这表明将学生的学习行为特征划分为5 个类别,对成绩的预测效果最佳。
梯度渐进回归树的参数初始范围设定为M={10,30,70,100},S={2,3,5},α={0.05,1,2,4}。在梯度渐进回归树模型训练过程中,使用均方根误差来描述迭代精度,计算方式如下:
式中,m表示的是样本数量,为样本实际数值,yi为预测数值。RMSE 的数值越小,则表明预测值越接近实际数值。训练及预测样本在模型迭代过程中的误差变化曲线如图3 所示。

图3 梯度渐进回归树均方根误差
从图中可以看出,训练和测试样本在迭代45 次后仍有下降的趋势,但变化较为缓慢。这表明模型已经趋于收敛,且此时的均方根误差约为0.004 5。值得注意的是,测试样本曲线与训练样本曲线走向一致,且测试样本曲线低于训练样本。这是因为测试样本的数量显著低于训练样本,所以在训练过程中训练样本RMSE 误差的降低未引发过拟合,因此也没有导致预测结果出现较大的偏差。
4 结束语
针对在线网络课程仅使用在线数据,难以预测学生成绩的问题,文中利用K-means 算法和梯度渐进回归树,构建出了一套成绩评估预测模型,并利用该模型对进行在线学习用户的成绩进行了预测。测试结果表明,所设计的模型能够实现较为精准的预测。但是需要注意的是,该研究结果仅适用于对一门课程的数据进行分析,因此该模型仍存在一定的局限性,有待于进一步研究实现多学科的综合评估。

