RBF 神经网络在动物动态称重中的研究

郭晨霞，李 达，杨瑞峰

（1.中北大学仪器与电子学院，山西太原 030051；2.山西省自动化检测装备与系统工程技术研究中心，山西太原 030051）

目前，动态称重数据处理算法有平均值算法、极大似然估计法、滤波法、EMD 算法、神经网络法等[1]，但是针对动物动态称重的研究比较少。机器视觉技术应用于无接触测量动物体重是热门研究方向，但是目前只能估测且成本较高[2]、难以适应规模化养殖的需求。孙建英研制的智能称重系统满足规模化需求，称重平均相对误差只有1.2%，但是样本小且未对算法进行深入研究[3]。在动态称重前对羊只进行一周的适应性训练，能有效降低平均相对误差[4]。在称重算法研究领域，Ma W 利用改进的限幅滤波算法和BP 神经网络降低肉鸡动态称重的误差[5]。唐思豪利用ADAM 改进的BP 神经网络对动态检重秤的砝码称重数据进行处理，能够准确估计动态称量结果[6]。魏赫通过粒子群优化RBF 神经网络算法对车辆动态称重数据处理后提升了动态称重的精度[7]。

针对动态称重数据样本不平稳、真实信号淹没在噪声中导致难以快速准确测量的问题，使用收敛速度快的RBF 神经网络对数据进行处理。通过与EMD 算法进行对比，验证RBF 神经网络在动物动态称重中的优越性。

1 RBF神经网络模型

利用RBF 神经网络模型处理动态称重数据本质是预测问题。将径向基函数（RBF）引入神经网络设计中，形成了RBF神经网络。RBF神经网络是一种由输入层、隐含层和输出层构成的三层前向型网络[8-9]。

输入层用于为网络传输预处理后的称重数据。隐含层完成对输入信号的非线性映射。输出层完成对各隐含层神经元输出的加权求和[10]。

高斯函数是RBF 神经网络中常用的径向基函数，因此径向基神经网络的激活函数可表示为：

RBF 神经网络的输出为：

式中，j=1,2,…,n；||xp-ci||为欧氏范数；xp为第p个输入样本；ci为网络隐含层结点的中心；σ为高斯函数的方差；wij为隐含层到输入层的连接权值；h为隐含层节点数；yi为与输入样本对应网络的第j个输出节点的实际输出[11]。

RBF 神经网络学习算法分为三步，第一步是求取基函数的中心，第二步是求解方差，第三步是求取隐含层和输出层之间的权值。

常采用K-均值聚类方法确定隐含层的中心[12]，径向基函数为高斯函数时，方差σi的求解公式为：

式中，i=1,2,…,h。cmax是所选取中心之间的最大距离。隐含层和输出层之间的权值可以通过最小二乘法直接计算得到，计算公式为：

K-均值聚类算法流程图如图1 所示。

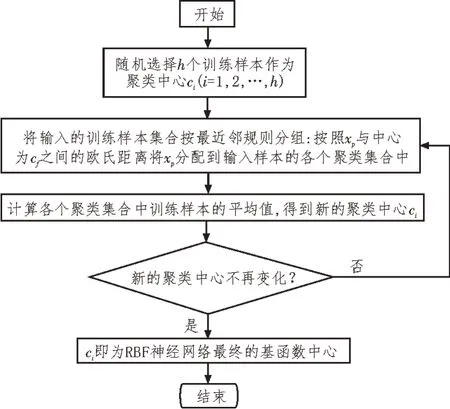
图1 K-均值聚类算法流程图

2 EMD动态称重模型

EMD 是由美籍华人Noden E.Huang 等在上个世纪九十年代提出的一种新的信号分析方法[13]，近年来被用于动态称重数据的处理，EMD 分解的信号包含真实的物理信号。一些学者认为动态体重测量值是静态体重和噪声叠加而成，静态体重可看作EMD分解的残余量，干扰信号可看作本征函数，所以通过EMD 逐步分解，最终可以得到残余量，也就是真实的体重值。

EMD 分解的过程为：

1）确定单个真值对应所有测量值的局部极大值和极小值点，用三次样条插值曲线将所有局部极大值点和局部极小值点连接起来，形成单次测量信号的上包洛线yup(t)、下包络线ylow(t)[14]。

沿河地区村庄成村较早，历史悠久。综合考虑日照、灌溉、饮水及防灾减灾等因素，聚落选址讲究，多位于沿河两岸较高的坪台上，背山面水，形成“山-水-田-人”共生共荣的人文景观（图2、3）。

2）按照式（5）获取上、下包络线的均值曲线：

3）x(t)减去平均值m1(t)后得到一个去掉低频成分的新序列h1(t)：

如果h1(t) 满足IMF 条件，则就得到x(t) 的首个IMF 分量h1(t)。

4）如果h1(t)不符合IMF 的条件，则将h1(t)作为初始数据，再次执行步骤（1）、（2），得到上下包络线的均值m11(t)，再判断式（7）是否符合IMF 条件：

如果不符合，则重复循环k次，得到：

当h1k(t)满足IMF 条件时，将h1k(t)赋值给c1(t)，这就是信号x(t)的第一阶IMF 分量。

5）将c1(t)从信号中去除，得到一个新的信号：

将Res1(t)作为新的原始数据重复上述步骤，得到第二阶IMF 分量，然后再重复上述步骤直到无法从剩余信号中提取满足条件的IMF 分量，剩余的信号记作Resn(t)，n为重复的次数。

3 动态称重实例分析

3.1 实验平台

文中使用的称重设备主要由装有四个称重传感器的秤台、高精度数据采集卡、控制台组成。其中控制台负责控制称重流程、读取和保存称重数据。图2所示为动态称重的简要过程。

图2 动态称重简要过程

3.2 实验数据的获取和预处理

三个不同体重的工作人员携带不同的砝码通过实验室搭建的称重平台获得2 967 组实验数据。实验数据包括称量物体的静态体重和四组传感器测量值。得到测量值以后，通过静态标定公式将四个传感器测量值转换为动态体重测量值，然后剔除三组存在极大误差的数据，将处理后的动态体重测量值和静态体重保存在Excel 表中。实验用到的静态标定公式如下：

其中，x1、x2、x3、x4分别为四个传感器的输出信号，x为传感器输出信号的和，y为动态体重。

3.3 实验过程及结果分析

3.3.1 EMD算法处理

将2 964 组实验数据中相同真值的数据提取出来，一共有96 组有共同目标体重的数据，对每组数据通过EMD 算法进行处理，由于每组数据两端的数据不一定是极值点，这样在数据两端无法画出准确的上下包络线，无疑为实验结果带来了误差而且误差层层累积[15]，为此采用镜像延拓法[16]对每组数据进行预处理后，再通过EMD 算法对每组数据进行分解，并取SD=0.2，得到的Resn(t) 即为想要的体重信号，对Resn(t) 求平均即可得到理想的体重测量值。实验结果如图3 和图4 所示。

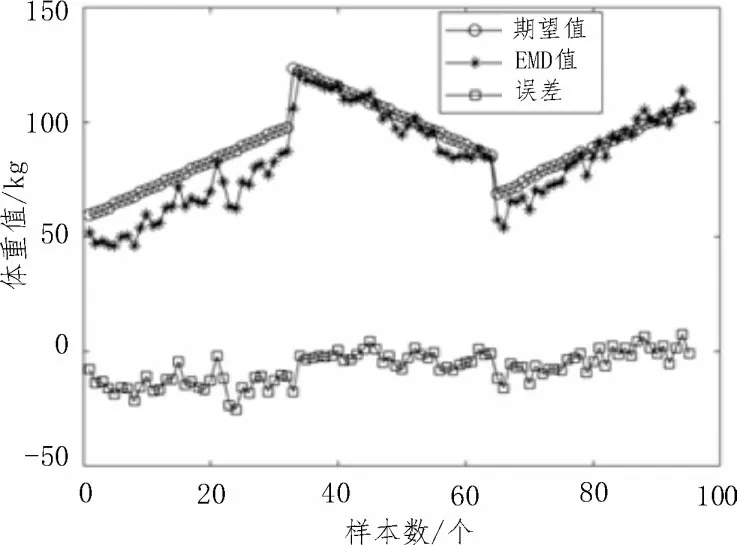
图3 EMD测试数据

图4 EMD测试数据相对误差

求得95 组数据的平均相对误差为9.523%，由图4 可知，样本数据中间和右端部分误差较小。

3.3.2 RBF算法处理

尽管EMD 算法对部分数据有较好的处理效果，但是其整体误差仍然较大，尝试利用径向基神经网络对数据进行处理。

首先对实验数据进行随机排序，然后选择前2 864 组数据进行训练，剩下的100 组数据进行测试。利用Matlab 中的newrb()函数对数据进行仿真实验，均方误差设置为0.01、径向基函数的扩展速度设置为1。RBF 神经网络训练过程中隐含层神经元个数增加到50 时，均方误差即不再改变，此时均方误差为0.047 87。训练结果如图5、图6 所示。

图5 RBF神经网络测试数据误差

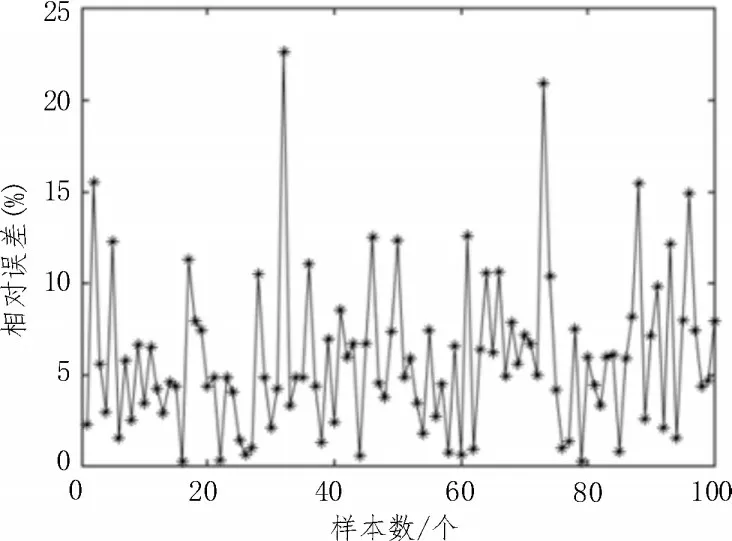
图6 RBF神经网络测试数据相对误差

由图6 可看出，RBF 算法对某些数据处理的误差接近0%，对动态称重数据进行10 次随机排序，并利用RBF 神经网络进行处理得到测试数据的平均相对误差为5.866%，将其视作RBF 神经网络算法的平均相对误差。

表1 为EMD 算法和RBF 神经网络对动态称重数据处理的对比，可以看出，RBF 神经网络是比EMD算法更有效的动态称重处理模型。

表1 EMD算法和RBF神经网络的比较

4 结束语

针对动物动态称重精度较低的问题，文中提出一种适用于动物动态称重的RBF 模型，实验结果表明，相比于EMD 模型，提出的RBF 拟合模型具有更高的精度，同时由于动物动态称重的复杂性，利用RBF 神经网络可以不对称重模型进行复杂的分析就可得到较为准确的数据，由此可以看出，RBF 神经网络在动物动态称重领域有实际的应用价值。