基于金豺优化算法的云计算资源调度研究

李伟彦，董宝良，王 凯，廉兰平

（1.华北计算技术研究所，北京 100083；2.中国电子科技集团有限公司，北京 100846）

云计算是一种基于互联网的计算方式，是在虚拟化计算和分布式计算的基础上发展而来的[1]。资源调度是云计算中的一个重要环节，具体来说就是根据云计算环境中的任务数量和资源情况，将任务分配到对应资源上并执行的过程[2]。

执行时间短、资源集群负载均衡一直是云计算资源调度问题中不断追求的目标[3]。为了优化云计算资源调度策略，国内外学者将传统算法和智能优化算法广泛应用于这一问题[4]，传统算法的代表如贪心算法[5]，较为经典的智能优化算法则有遗传算法[6]等，但这些算法并不是完全适配于云计算资源调度模型[7]。

金豺优化算法由Nitish Chopra 和Muhammad Mohsin Ansari 于2022 年提出，是一种模拟金豺合作狩猎提出来的群体智能优化算法[8]。金豺优化算法的优点是收敛速度快且收敛精度高，局限性是目前仅能应用于单目标优化。实验将该算法应用于云计算资源调度策略的单目标优化。

1 金豺优化算法介绍

1.1 算法思想

金豺优化算法模拟了金豺合作狩猎的行为，通过猎物位置的更新来实现算法的寻优过程。在金豺优化算法中，猎物种群的初始位置在全局搜索空间上随机产生。将每次猎物种群位置变更后处于最优位置的个体作为雄性金豺，处于次优位置的个体作为雌性金豺，并利用金豺夫妇的位置对猎物种群的位置进行变更。也就是说，在金豺优化算法中，金豺对是猎物的一部分。

算法根据猎物的能量来划分金豺搜索、包围和攻击猎物的过程。当猎物能量较高时，金豺搜索猎物的过程由雄性金豺带领，雌性金豺跟随。当猎物的能量低于某个阈值之后，金豺夫妇会包围并攻击猎物。

1.2 算法设计

1.2.1 种群位置初始化

每一只猎物的位置随机分布在搜索空间上：

其中，Xi,j表示第i只猎物在第j维空间的位置，Xj,max和Xj,min分别表示第j维空间的上边界和下边界，random()为[0,1]内的随机数。最终形成的猎物种群位置矩阵如下：

其中，m为猎物种群的大小，n为搜索空间的总维度。

1.2.2 确定雌雄金豺对位置

根据猎物种群位置矩阵以及特定的适应度函数计算适应度矩阵，位置具有最优适应度的猎物记为雄性金豺，位置记为XM，适应度记为fM；位置具有次优适应度的记为雌性金豺，位置记为XFM，适应度记为fFM。

1.2.3 搜索猎物阶段

在搜索猎物阶段，雄性金豺对于猎物种群中每个个体的相对位置如下：

雌性金豺对于猎物种群中每个个体的相对位置如下：

其中，t为当前迭代的次数，Xi(t)表示第t次迭代时第i个猎物的位置，YM(t)表示第t次迭代时雄性金豺的位置，YFM(t)表示第t次迭代时雌性金豺的位置。E为逃跑能量，计算公式如下：

其中，E0为初始逃跑能量；E1为一个系数，用来递减逃跑能量E；T为总迭代次数；C1为常数，取值为1.5。E1随着迭代次数的变化，由1.5 逐渐减小至0；E0为[-1,1]内的随机值。

作者对E0的取值方式和对式（4）、（5）两式的设计参考了哈里斯鹰优化算法。

式（3）、（4）中的rl表示一个m×n维的基于levy分布的随机向量，其公式如下：

其中，u和v均为[0,1]内的随机值，β为常数，设为1.5。

1.2.4 包围攻击猎物阶段

在包围攻击猎物阶段，雄性金豺对于猎物种群中每个个体的相对位置如下：

雌性金豺对于猎物种群中每个个体的相对位置如下：

1.2.5 猎物种群位置变更

在金豺优化算法中，金豺对搜索猎物阶段和包围攻击猎物阶段，猎物种群位置变更所使用的公式相同，如下：

其中，Xi(t+1)表示第t+1 次迭代，即下一次迭代时第i个猎物的位置。

2 云计算资源调度模型

2.1 基本概念

Map/Reduce 分布式处理框架是当前云计算的关键技术之一，主要用于云计算中对大数据的处理[9]。Map/Reduce 的核心思想是将庞大的任务分割成若干个简单的任务，分别在不同的处理机上执行，最终对分布式处理的结果进行汇总[10]。

在基于Map/Reduce 思想的云计算资源调度模型中，由数据中心生成虚拟任务集，再由调度中心通过算法对任务集进行调度，分配至各虚拟机节点执行，即Map/Recude“分而治之”的思想[11]。而对调度算法优化的目标，一般是针对所有任务执行结果的全局目标，即Map/Reduce分布式处理框架中“合”的思想[12]。

2.2 数学模型

设虚拟机用户节点共有n个，分别用Vi表示每个虚拟机的处理能力，构成集合V={V1,V2,…,Vn}，单位为MIPS。由数据中心生成m个任务，分别用Ti表示每个任务的指令数，构成集合T={T1,T2,…,Tm} 。则第j(1 ≤j≤m) 个任务在第i(1 ≤i≤n) 个虚拟机上处理的时间为：

式中，t的单位为微秒(μs)。

在对任务分配完成后，每个虚拟机的执行总时间为：

式（11）中的j为在第i个虚拟机上执行任务的编号集合。

实验是单目标优化，目标为减少云计算任务的执行总时间，故适应度函数应设置为执行总时间最长的虚拟机的执行时间的倒数：

3 仿真过程及结果

3.1 实验配置

文中实验基于Cloudsim仿真环境[13]。利用Python产生[100,999]内的整数共100 个，作为100 个虚拟机的执行能力；利用Python 产生[10 000,99 999]内的整数共10 000 个，作为10 000 个任务的大小。

将贪心算法、遗传算法和金豺优化算法分别在Datacenter Broker 类中实现[14]。设置遗传算法的参数如下:种群大小为20，迭代次数为50，交叉概率为0.8，变异概率为0.01，这是遗传算法在云计算资源调度模型下以任务总完成时间为优化目标的实验结果较好的参数配置[15]。

在金豺优化算法中，将猎物位置类比为所有任务对虚拟机的选择序列，在每次猎物位置变更后对猎物位置都进行四舍五入取整操作，并对超出搜索空间范围的猎物位置进行修正，将猎物的种群规模设置为40。

3.2 实验流程

首先，在不同迭代次数、相同虚拟机个数以及相同任务个数下调度金豺优化算法进行实验，求得金豺优化算法在云计算资源调度模型下以任务完成总时间为优化目标的最优迭代次数。然后，对金豺优化算法使用最优迭代次数，在不同虚拟机个数和任务个数的条件下对三个算法分别进行调度，分别做10 次重复实验，结果取10 次实验的平均值[16]。对比实验数据，判断金豺优化算法相较于其他算法所适用的数据规模。

在实际实验过程中，发现原本的金豺优化算法的实验效果不佳，于是调整了式（6）的参数，并取得了较好的实验效果[17]。下文所有基于金豺优化算法的实验数据均是调整参数后的实验结果。

3.3 GJO迭代次数实验

设置参加仿真的任务为1-1 000 号的1 000 个任务，设置参加仿真的虚拟机为1-10 号的10 台虚拟机，设置金豺优化算法的迭代次数分别为20、40、60、80、100、120、140、160、180、200，仅使用金豺优化算法参与仿真实验，得到图1 所示的实验结果。

图1 GJO在不同迭代次数下的实验结果

由图1 中的实验结果可知，金豺优化算法的效果在迭代次数小于100 时会随着迭代次数增加而优化，在迭代次数大于100 时随着迭代次数增加并无明显优化，即可以认为100 为金豺优化算法在云计算资源调度模型下以任务完成总时间为优化目标的较优迭代次数。

3.4 三种算法不同任务数量下的实验

设置参加仿真的虚拟机为1-10 号的10 台虚拟机，设置金豺优化算法的迭代次数为100，先取前20、40、60、80、100、120、140、160、180、200 个任务参与实验，再取前1 000、2 000、3 000、4 000、5 000、6 000、7 000、8 000、9 000、10 000 个任务参与实验，分别代表小数据规模和大数据规模下的仿真，同时使用贪心算法、遗传算法和金豺优化算法进行仿真实验，得到图2 和图3 所示的实验结果。

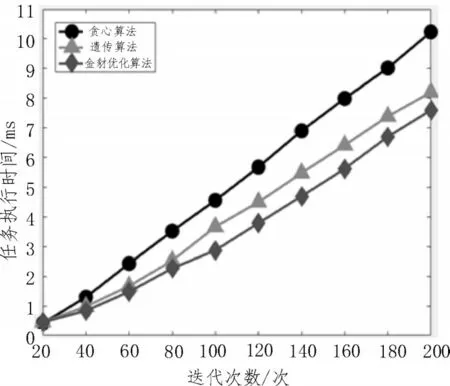
图2 小数据规模下三种算法仿真结果

图3 大数据规模下三种算法仿真结果

由图2 中的实验结果可知：1）在任务数量为20时，金豺优化算法在资源调度时的效果是最差的；2）当数据量逐渐增大时，金豺优化算法在资源调度时的效果逐渐变好，但在任务数量小于80 时效果仍不明显；3）在任务量达到200 左右时，金豺优化算法的效果已完全优于贪心算法，但对于遗传算法的优越性仍不明显。

由图3 中的实验结果可知：1）在任务数量大于1 000 时，贪心算法相较于其他两种算法效率较低；2）金豺优化算法相较于遗传算法的优势逐渐明显，且优化程度趋于稳定；3）在数据量足够大时，金豺优化算法相对于遗传算法对云计算任务执行的效率提高了约20%。

3.5 三种算法不同虚拟机数量下的实验

设置参加仿真的任务为1-1 000 号的1 000 个任务，设置金豺优化算法的迭代次数为100，分别取前10、20、30、40、50、60、70、80、90、100 台虚拟机参与实验，同时使用贪心算法、遗传算法和金豺优化算法进行仿真实验，得到图4 所示的实验结果。

图4 不同虚拟机数量下三种算法仿真结果

由图4 中的实验结果可知：1）虚拟机个数对三种算法的仿真结果有很大影响；2）在虚拟机个数相对较少，即单个虚拟机分配云计算任务个数相对较多时，金豺优化算法的优势更明显。

4 结论

针对云计算环境下资源分配不均的问题，以任务总完成时间为优化指标，可以简单直接地提升资源利用效率，使任务得到及时处理。金豺优化算法是一种单目标优化算法，在云计算资源调度实验场景下，以大规模任务为前提，设置特定迭代次数，以任务总完成时间为优化指标，金豺优化算法相较于其他很多算法实验效果更好。综上，金豺优化算法对真实的云计算资源调度场景具有很高的实际应用价值。