疾病信息传播对疾病传播的影响

汪洋

摘   要：疾病传播过程中，易感人群可提前获得疾病信息并采取防护措施，从而抑制疾病传播。运用平均场方程和系统动力学方法来建模信息传播和疾病传播复杂系统，结果表明，政府及时发布疾病信息和个体主动自我防护，在疫情传播期间会有效抑制病毒的传播。在新媒体环境下，疾病信息的传播速度要比疾病本身传播更快，这种“速度优势”对于抑制疾病传播的意义重大，可以帮助人们更好理解疾病信息传播对疾病传播的影响，可以为疾病防控和舆情管理提供指导。

关键词：疾病信息传播；疾病传播；平均场方程；系统动力学

中图分类号：R18       文献标志码：A      文章编号：1673-291X（2023）12-0138-04

引言

从1976年埃博拉病毒惊现，到2003年“非典”席卷全球，再到2019年新冠疫情的爆發，世界性的公共卫生事件并不是小概率事件。所以，从人类健康和疾病防控的角度出发，研究病毒传播的影响因素以及掌握病毒传播的规律具有十分重要的意义。

双层网络是一种经典的网络结构，它被应用到了广泛的研究领域[1，2]。在疾病传播的双层网络研究中，基于平均场方程求解传播过程的阈值大多被用来分析两层网络间的相互作用。平均场方程可在微观上准确模拟疾病信息传播过程。但是现有的双层网络研究中，受限于模型的复杂程度，通常只能纳入有限的变量。而系统动力学方法是在宏观上模拟疾病传播过程，通过系统动力学方法建立的仓室模型可以模拟传播过程。然而，系统动力学无法对疾病信息传播的微观过程进行模拟，无法考虑网络拓扑结构对传播的影响，难以区别知道疾病信息并采取防控措施的个体和不知道疾病信息并未采取防控措施的个体。

因此，本文通过构建疾病信息传播和疾病传播的双层网络，创新性地结合了平均场方程和系统动力学方法，来研究疾病信息传播对疾病传播的影响。本文的研究意义在于：（1）为疾病信息传播对疾病传播的研究提供新的方法论；（2）可以帮助人们更好认识疾病信息传播对疾病传播的影响，可以为疾病防控和舆情管理提供政策支持。

一、方法

（一）模型假设

本文构建了一个疾病信息传播影响下的疾病传播双层网络，如图1所示。在经典的SEIR模型中，疾病层的个体可能具有四种状态，即易感者、暴露者、感染者和康复者。它没有考虑疾病信息传播的影响，并忽视了不同行为状态的易感人群对疾病传播动态的影响。在双层网络中，信息层的个体有三种状态，即无知者Ii、传播者Si和移出者Ri；疾病层的个体可能具有五种健康状态，即采取防护措施的易感者DSd、未采取防护措施的易感者USd、暴露者Ed、感染者Id和恢复者Rd。根据是否采取了防护措施，个体存在两种状态，即采取防护措施的传播者DSi和采取防护措施的移出者DRd。传播者和移出者作为“知情者”是了解疾病信息的个体，他们会根据自身掌握的疾病信息选择是否采取防护措施。而无知者由于未获得疾病信息，只能“无动于衷”。相应地，在疾病传播层上，我们关注在信息传播的影响下易感人群的行为变化。根据是否采取了防护措施，它们被分为普通易感者和采取防护措施的易感者。本文做了两个假定：（1）疾病信息的传播过程随着疾病传播的开始而开始，在疾病传播开始前个体均未采取针对它的防护措施。（2）在信息传播过程中，个体主要通过社交媒体、亲身感受等各种途径获得疾病信息，继而根据获得的疾病信息主动选择是否采取防护措施，并且个体是否采取防护措施并不影响信息的传播过程。

（二）Info-SEIR模型

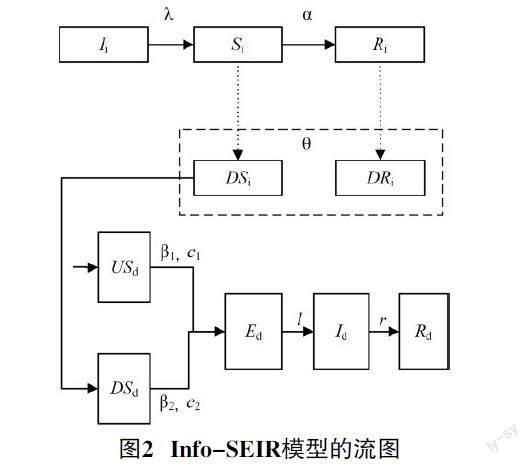
我们改进了经典的SEIR模型，得到新的疾病传播仓室模型—Info-SEIR，如图2所示。它的新特征体现在两个方面。一方面，易感者可能具有两种不同的状态，即未采取防护措施和采取了防护措施。采取了防护措施的易感者感染风险更低，对应的单次接触感染率和每日平均接触次数更低。另一方面，这两类易感人群在群体中所占的比例随着疾病信息传播而变化。

疾病传播过程中，个体的行为变化受到疾病信息传播的影响。在疾病开始传播前，信息层的所有个体均是无知者。当疾病层出现感染者，信息层立即出现疾病信息的传播者，信息传播过程随之开始。根据经典的SIR模型，个体可能存在三种状态，即传播者、无知者和移出者。为了刻画疾病信息传播过程中个体行为的变化，我们建立一个带有个体行为变化的疾病信息传播模型。传播者在社交网络上传播疾病信息，并影响与他相邻的个体。清楚的是，传播者和移出者都获得了疾病信息，是“知情者”，会决定是否采取防护措施；而无知者未获得疾病信息，也就没有行为上的改变。

在仓室模型中，参数N、c1、β1影响了USd到Ed的流量，参数N、c2、β2影响了DSd到Ed的流量，1/l影响了Ed到Id的流量，r影响了Id到Rd的流量。基于传播动力学，疾病传播的Info-SEIR模型可通过以下微分方程刻画：

I'i，k=-λ k Ii，k ∑k'Si，k P（k'/k）

S'i，k=λ k Ii，k∑k'Si，k P（k'/k）-α k Si，k∑k'[Si，k' + Ri，k'] P（k'/k）

R'i，k=α k Si，k ∑k'[Si，k' + Ri，k'] P（k'/k）DS'i = Si θ

DR'i= Ri θ

D'i= DSi+DRi

E'd= USd β1 c1 （Ed + Id） + DSd β2c2（Ed+Id）-Ed / l

I'd=Ed / l-Idr

R'd=Idr 其中，

USd=（N-Ed-Id-Rd）（1-Di） / N （2）

DSd = （N-Ed-Id-Rd）Di / N （3）

（三）信息传播网络特征

假设个体在信息传播层构成一个无标度网络[3]，其中，节点数量为10 000，边的数量为99 900。网络密度d代表的是节点之间联络的紧密程度，d=2m/n（n-1），它的值为0.002。网络传递性T=0.01，代表认识同一节点的两个节点相互认识。

二、数值模拟

这个部分展示了Info-SEIR模型的仿真结果和分析。数值模拟和仿真的工具为PyCharm2020.3.3 IDE和Vensim 7.3.5。我们分别探讨了信息传播对疾病传播的影响以及传播率、行为改变率、移出率对疾病传播的影响。

（一）疾病信息传播对疾病传播的影响

为了评估疾病信息对疾病传播的影响，我们比较研究了Info-SEIR模型和未考虑疾病信息传播影响的SEIR模型，如图3所示。结果表明，Info-SEIR模型降低了感染者的密度，与SEIR模型相比，Info-SEIR模型的每日新增确诊病例和累计确诊病例密度曲线更平滑且数值更低。信息传播可在不同程度上抑制疾病扩散，并且β2和c2值越大抑制作用越明显。其中，当β2和c2值为0.011 3时，Info-SEIR模型的每日新增感染者和累计确诊病例曲线最平滑且数值最低，此时疾病信息传播对疾病扩散产生了最强的抑制作用。相较而言，Info-SEIR模型中，每日新增病例的曲线更平缓且顶点更低，疾病扩散的程度更轻；累计确诊病例的曲线同样更平滑，且数值更小。可以发现，疾病信息传播在疾病传播过程中会抑制疾病扩散，并且抑制的程度不同。这种抑制作用是因为易感人群采取了防护措施，降低了自身的感染风险。

累计感染者的密度随着β2和c2变化的变化

疾病信息传播通过行为因素来影响疾病的传播。因此，我们评估了疾病信息传播对个体行为变化的影响。建模结果表明，疾病信息的传播要先于个体主动采取防护措施，并且很快达到稳定水平，如图4所示。在疾病信息传播过程中，传播者的密度Si快速增加后逐步减少；无知者的密度Ii不断减少，最终达到稳定水平，而移出者的密度Ri呈现不断增加的趋势，最终在达到稳定水平。此后，群体中只存在无知者和移出者。而个体行为的改变并未停止，采取防护措施者的密度仍在不断增加，最终达到最大水平，此时群体的防护力达到最大。社交媒体上的信息传播快速，疾病防控部门可以借此及时发布疾病相关信息，以帮助公众进行自我防护。

（二）行为改变率对疾病传播的影响

这部分探讨了行为改变率函数对疾病传播的影响。行为改变率是个体在获得疾病信息后主动采取防护措施的概率，由行为改变率函数确定。图5表明，行为改变率函数的变化影响了群体防护力的变化趋势，且对疾病传播动态产生了不同的影响。我们选用t=50时采取防护措施者密度来表示此时的群体防护力水平，并记为D60，来探讨行为改变率函数变化对群体防护力的影响。为了便于观察D60随u2和v2的变化，我们对仿真结果进行了多项式拟合。图5中，左图为D60随u2和v2变化的变化；右图为I60随着u2和v2变化的变化。拟合方程为如下：

D60=0.697-0.026×u2+0.008×v2-0.052×u2×v2+v2（6）

I60=0.0002375-0.00028×u2-0.00008607×v2（7）

根据拟合的评价参数，在95%的置信区间，R2=

0.840 8，拟合结果可以很好地反映D60随着u2和v2变化而变化。结果表明，随着u2的增加，D60表现出下降的趋势。当u2=1和v2=1时，D60取得最小值0.001 1；当u2=0和v2=1时，取得最大值0.001 4。而随着v2的增加，D60的变化出现了两种情况，一是随着v2的增加，D60表现出下降的趋势；二是随着v2的增加，D60表现出上升的趋势。

我们选用了t=60时每日新增感染者密度来表示此时疾病扩散的程度，记为I60，并通过调整行为改变率函数的参数u2和v2，来观察疾病传播动态的变化。为了便于观察I60随u2和v2的变化，我们对仿真结果进行了多项式拟合，如图5所示。根据拟合的评价参数，在95%的置信区间，R2=0.913 8，拟合结果可以很好反映I60随着u2和v2改变的变化趋势。结果表明，I60随着u2增大而增大。而I60随着v2的变化有两种情况，一是I60随着v2的增加而增加，如u2=1时；二是I60随着v2的增大而减小，如u2=0。u2增大使得群体防护力降低，从而疾病扩散更严重。而v2对群体防护力影响的两种情况解释了v2对疾病传播动态影响的两种情况，一是v2增加使得群体防护力降低，从而疾病扩散更严重；二是v2增加使得群体防护力增强，从而疾病扩散更轻。总之，行为改变率函数的变化影响了群体防护力的變化趋势，导致了不同的疾病传播动态。

三、结束语

当前，很多社交媒体被用来发布有关疾病的重要信息[4]，在病毒传播时，社交媒体（如推特、脸书、微信等）为政府和公众获取、分享和传播确诊病例数、感染症状、预防措施等信息发挥了重要作用[5]，也帮助减少了接触人数，缩短了病毒传播的持续时间[6]。本研究提出的模型具有如下一些新的特征和显著结果。

首先，我们创新性地采用了平均场方程和系统动力学方法，并建立了疾病传播的双层网络模型——Info-SEIR模型。据调查，目前研究中尚未涉及两种方法的结合。我们的研究可以为疾病传播的研究提供新的方法论。其次，我们的建模结果可以帮助更好理解疾病信息传播和个体自我防护在疾病传播过程中的影响，并为疾病防控和舆情管理提供了相关引导。

然而，我们的研究仍存在一些不足和拓展空间。例如，我们选用了无标度网络来构建疾病信息传播的社交网络，但是研究中并没有考虑无标度网络的相关特征对建模结果的影响。在未来，我们考虑将模型应用到其他类型的网络结构中，用来探究不同网络拓扑结构对模型和结果的影响。

参考文献：

[1]   A Belyi，I Bojic，S Sobolevsky，I Sitko，B Hawelka，L Rudikova，A Kurbatski and C Ratti[J].Global multi-layer network of human mobility[J].Int J Geogr Inf Sci，2017，31（7）：1381-1402.

[2]   张瑞霞.二部网络上媒介传染病传播模型的动力学分析[J].云南师范大学学报，2021，41（4）：47-55.

[3]   惠英文.基于无标度网络的SPANR信息传播动力学模型[J].信息与电脑，2022，34（8）：48-50.

[4]   付伟.动态同质网络上的SIR谣言传播模型[J].计算机应用，2018，38（7）：1951-1955，1966.

[5]   Y Lu and L Zhang.Social media WeChat infers the development trend of COVID-19[J].J Infect，2020，81（1）：e82-e83.

[6]   C Sun，W Yang，J Arino and K Khan. Effect of media-induced social distancing on disease transmission in a two patch setting[J].Math Biosci，2011，230（2）：87-95.

Research on Public Opinion Management under Public Health Emergencies

Wang Yang

（Business School， University of Shanghai for Science and Technology， Shanghai 200093， China）

Abstract： During the disease spread， susceptible people can obtain disease information in advance and take protective measures to suppress the disease spread. Mean field equations and system dynamics methods were applied to model the complex system of information dissemination and disease spread. The results show that the timely release of disease information and individual self-protection by the government will effectively suppress the spread of the virus during the epidemic transmission. Moreover， in the new media environment， disease information spreads faster than the disease itself. This “speed advantage” is important for suppressing the spread of disease. Our work can help better understand the impact of disease information dissemination on disease transmission， and can guide disease prevention and control and public opinion management.

Key words： disease information transmission; disease spread; mean-field equation; system dynamics

[責任编辑   妤   文]