基于随机森林回归的砂体渗透系数预测

刘富强，陈晓冬，李盛富，张福衡

（核工业二一六大队，新疆 乌鲁木齐 830011）

砂岩型铀矿床砂体渗透系数既是影响地下水渗流方向和溶质运移的重要因素［1］，也是砂体非均质性评价的重要参数。一般情况下，获取砂体渗透系数的方法有两种，即抽水试验和样品分析。抽水试验能够确定其影响半径范围内的渗透系数，但试井施工代价高，分布稀疏，很难获得既有试井影响半径范围之外的渗透系数；样品分析的代表性不足，且在样品采集和测定过程中存在不可避免的误差。因此，渗透系数预测及其空间分布特征是铀矿勘查最为困难的问题之一［2］。

地球物理测井资料具有分辨率高、信息量大的特点，能够直接反映纵深方向上物性变化的属性，具有很高的研究及应用价值［3］。将测井信息转化为地质参数是测井评价的主要任务，随着勘探深度不断加大，铀矿勘探面临着更为复杂的地质结构，更加高昂的勘探成本［4］，因此，对传统测井评价和测井数据分析提出了更高的要求，测井精细化评价面临巨大挑战。在地质信息化大背景下，大量的地质信息数据库不断建立和完善，如何从海量测井资料中提取出更有价值的信息已成为改进铀矿勘探效率的重要方面。随着机器学习算法广泛应用于地质及地球物理领域中，比如神经网络算法［5-6］、支持向量机算 法［7-8］、朴素贝叶 斯算法［9］、随机森林算法［11-12］等，它们将测井评价过程转化为机器学习过程，相较于线性数学模型，能够有效解决测井评价中复杂的非均质性问题。但各类机器学习算法也存在着一些自身不足，如神经网络算法易陷入局部极小值，支持向量机算法原理复杂且训练难度较大等。因此，寻找更简便快捷的机器学习算法应用于砂体渗透系数预测具有重要的研究意义。本文采用随机森林回归算法，以洪海沟铀矿床为研究对象，对砂体渗透系数进行预测，以期解决该地区砂体渗透系数空间分布特征问题。

1 机器学习算法概述

机器学习是利用计算机技术从海量不确定性的历史数据中挖掘有意义的变化规律，主要用来解决分类和回归问题，通过建立机器学习模式，不断改进算法提高准确度，进而识别新的数据或预测未知数据。19 世纪50 年代机器学习概念被提出，1980 年举行的第一届机器学习研讨会掀起了机器学习研究的热潮。2000 年以后，随着机器学习技术及计算机硬、软件的蓬勃发展，机器学习在各行各业得到了广泛应用。机器学习通过“训练样本”得到效果较好的“学习模型”，并能很好地适用于“新样本”，具有很强的泛化能力。通常情况下，“训练样本”越多，能得到的关于样本集的规律信息就越多，随着训练任务的不断执行与经验的累积，获得泛化能力强的“学习模型”可能性越大［13-14］。随着各领域学者对机器学习研究的不断深入，也给铀矿勘查中测井精细化评价带来了更加广阔的发展和应用前景。然而，机器学习算法众多，每类算法都有其适用条件和优缺点，应根据具体的地质问题选取合适的机器学习算法，以期达到较好的预测效果。

2 随机森林回归算法

2001 年，Breiman 提出了随机森林算法（Random Forests，简称RF）［15］。该算法最初主要用来处理分类问题，随着研究的深入，也解决了许多回归问题，目前已成为数据挖掘领域中非常重要的成员。随机森林算法以统计学理论为基础，首先用重抽样方法（Bootstrap）有放回地从原始样本中抽取多个样本；其次，以决策树为基学习器对每个样本建模，并对所有预测结果进行组合；最后，分别使用投票和平均的方法给出分类问题和回归问题的预测结果。随机森林算法是决策树的扩展运算，众多的决策树组合成了随机森林，即将若干非线性关系组合成一个更加复杂的非线性关系。

目前，在地球物理领域和测井评价方面对随机森林算法的应用和研究不多，且主要用来处理分类问题，如使用航空地球物理数据进行岩性分类识别，使用测井数据进行储层的岩性识别［16］，使用地震属性进行储层特征参数预测等［12］。在砂岩型铀矿勘查中，地球物理测井数据能够提供大量精细的地下信息，而砂体渗透系数是一项重要的水文地质参数，它们之间表现为一种复杂的非线性关系，不同类型的测井参数对砂体渗透系数会有不同的响应特征，而砂体渗透系数预测问题的难点就是如何选取一种合适的算法进行回归预测［17］。随机森林算法处理回归问题具有调节参数少、操作简单、抗噪性强、预测准确率高的优点，运算时对数据具有较高的“容忍度”，且不易出现“过拟合”、“欠拟合”或算法不收敛的问题。为了解决测井数据与砂体渗透系数之间非线性关系的复杂性问题，将随机森林回归算法（Random Forests for Regression，简称RFR）引入到渗透系数预测中。利用随机森林回归算法预测砂体渗透系数基本步骤如下（图1）：

图1 随机森林回归渗透系数预测示意图Fig.1 Schematic diagram for the prediction of permeability coefficient by random forest regression

1）样本集：提取对渗透系数有响应的原始测井数据属性作为输入变量x，筛选原始渗透系数作为输出变量y；将原始测井数据与渗透系数组成原始样本集；

2）抽样集：采用Bootstrap重抽样法随机且有放回地对原始样本集进行抽样，生成多组抽样集，每组抽样集形成了由被抽中与未被抽中（称为袋外数据）的两种数据组成的一颗决策树；

3）生长：每棵决策树从输入变量x中随机选取若干个特征作为当前节点分裂子集，依据Gini 指标选取最优特征进行分裂使每棵回归决策树得到最大限度的生长；

4）检验：袋外数据未参与建模过程，可利用其检验模型效果与精度。根据袋外数据的预测误差进行重新建模，以确定最佳决策树数目；

5）预测：对于需要预测的输入变量xi，i=1，2，…，k，每棵决策树都会输出相应的预测值yi，i=1，2，…，k，随机森林回归的预测值即为所有决策树的预测值的平均值。

随机森林回归算法中每棵决策树均抽取原始样本集中的一部分属性进行建模，如此反复抽样能极大的提高预测模型的多样性，使得每棵决策树之间的相关性最小化。

3 随机森林回归应用

3.1 地质概况

伊犁盆地南缘是我国砂岩型铀矿产出地，近年新发现的洪海沟铀矿床位于伊犁盆地南缘斜坡带西部构造简单的相对稳定区洪海沟微凹，主要含矿层自上而下有头屯河组、西山窑组上段、西山窑组下段及八道湾组，含矿岩性以细砂岩、中粗砂岩为主，为典型层间氧化带砂岩型铀矿床［18-19］。

随着对洪海沟铀矿床主要含矿层砂体发育及铀矿化控因的精细化研究，认为砂体的空间展布约束着层间氧化流体的运移，而砂体渗透系数空间分布造成层间氧化带分层，进而控制铀矿体的空间产出状态。目前在矿床内仅完成10 组水文参数孔，并通过抽水试验计得到了10 组渗透系数，整体上看数量较少且分布不均匀。因此，利用遍布矿床的测井数据开展砂体渗透系数预测研究，有助于该区铀矿成矿模型的建立，并且对分析其他具有类似条件的找矿工作具有重要意义［2］。

3.2 随机森林回归

在砂岩型铀矿勘查钻孔施工过程中，受岩心采取率和钻进影响，取样位置与实际测井位置存在不可避免的误差。因此，在洪海沟铀矿床孔渗样品分析结果与测井数据的相关性不是很高的情况下，需探寻其他资料来研究洪海沟铀矿床砂体渗透系数预测问题。视电阻率测井是观测区域内地下三维空间体的综合反映，而水文参数孔抽水试验观测的渗透系数也是其抽水半径范围内的综合体现，从观测结果上看，视电阻率测井数据与抽水试验渗透系数本质上均属于间接观测，且均是一定范围内地下信息的综合响应。因此，选取视电阻率测井数据、砂体厚度及抽水试验渗透系数作为原始样本集，进行随机森林回归预测具有较好的数据基础。

3.2.1 随机森林回归构建过程

1）从原始样本集中使用重抽样法随机有放回地抽取m 个样本，共进行n 次抽样，生成n个训练集；

2）n 个训练集分别生成n 个决策树模型，对每个决策树模型根据基尼指数选择最好的特征进行分裂，在分裂过程中得到最大限度的生长；

3）n 个决策树模型组成随机森林模型，随机森林回归预测结果取n 棵决策树预测的平均值作为最终预测值。

3.2.2 随机森林回归模型评价

利用10 组样本数据训练随机森林模型，确定2 个变量与渗透系数之间的非线性关系。图2 为训练过程中随机森林回归决策树数量与袋外数据检验均方误差及模型对数据的拟合优度关系图。从图中曲线可以看出，决策树小于25 棵时，随决策树的增多，袋外均方误差逐渐降低，拟合优度逐步提高；当决策树为25 棵时，袋外均方误差降到最小值0.352%（图2a），此时拟合优度达到0.950（图2b）；决策树在26～100棵时，袋外均方误差和拟合优度均有一定的扰动；决策树大于100 棵以后，袋外均方误差和拟合优度趋向变化平稳。因此，选取决策树为25棵建立模型用于该地区砂体渗透系数的预测。

图2 随机森林回归决策树数量与袋外数据均方误差（a）及拟合优度（b）关系图Fig.2 The mean square error（a）and goodness（b）of fit outside the bag to the number of decision trees by random forest regression

3.3 回归结果对比

利用随机森林回归建立洪海沟铀矿床砂体渗透系数预测模型，分别选取10、25、200 棵决策树进行随机森林回归预测。此外，使用非线性回归［2］及支持向量机方法的结果与随机森林回归进行比较分析，其中非线性回归选取对数型模型，支持向量机选用惩罚系数分别为0.05 和0.50 的高斯核函数（RBF）及最高幂次分别为2 次和4 次的多项式核函数（Poly），发现不同的机器学习算法均可以实现回归预测，但其结果有一定的差别（表1、图3）。

表1 回归结果对比一览表Table 1 List of regression results

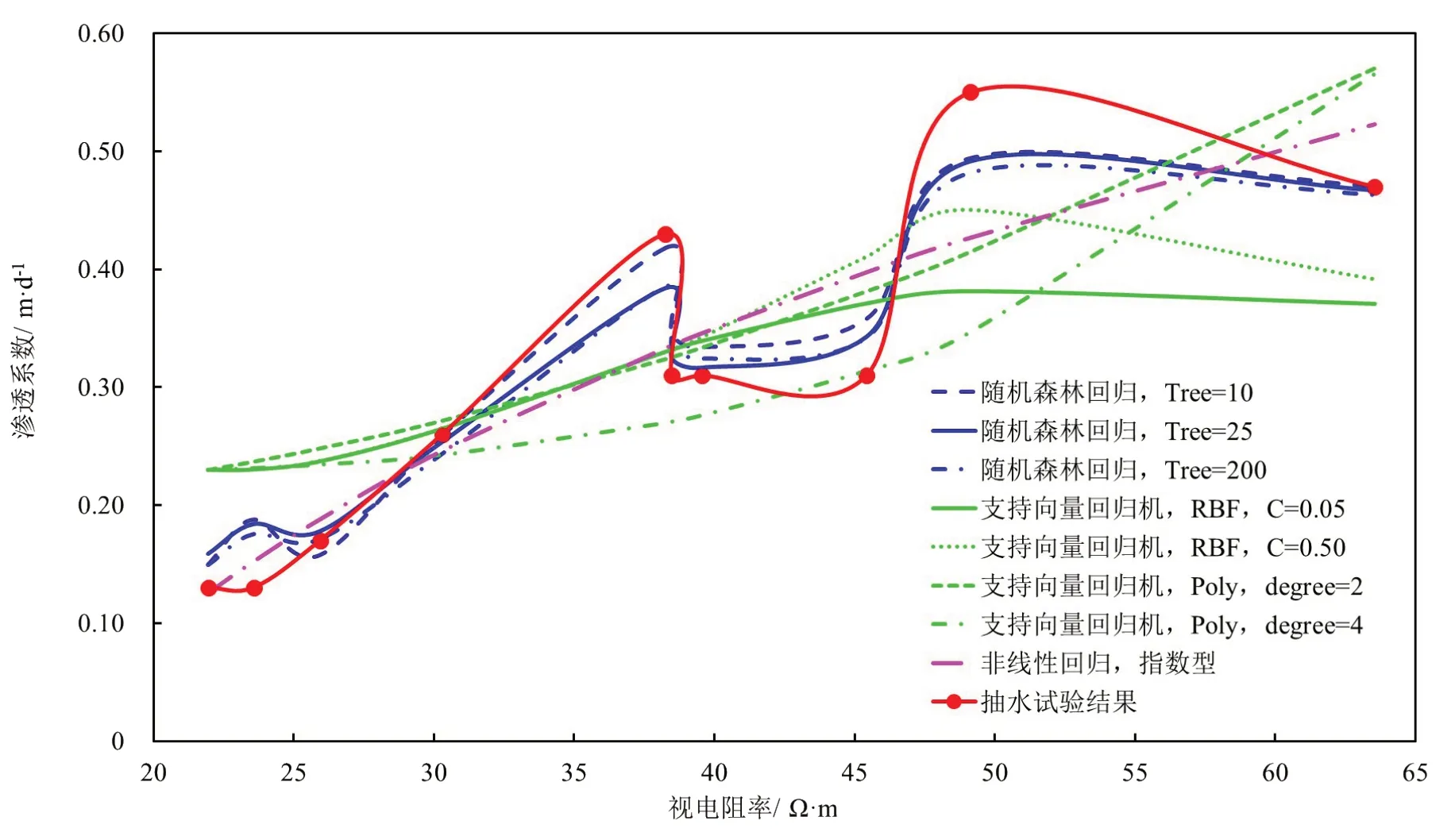
图3 回归结果对比图Fig.3 Comparison of regression results by different method

非线性回归算法预测数据与抽水试验数据之间的拟合优度为0.794，结果较为准确，但该算法需要事先确定曲线类型，无论通过经验推断或观测散点图确定曲线类型，均受人为因素影响较大，算法泛化能力及迁移学习能力均较弱。

支持向量回归机算法对样本集进行训练和预测时，选取不同的核函数及相应参数，拟合优度在0.445～0.785 之间变化，说明结果的稳定性不是很好，主要原因有两个，一是对核函数的选择需要进行模型先验，二是样本集数据量少，回归效果不是很理想。该方法优于非线性回归法，主要表现在较强的自适应能力和泛化能力，缺点是对核函数的选择还需要一定的先验信息。

分别选取10、25、200 颗决策树进行试验，拟合优度在0.938～0.950 之间变化，结果优于非线性回归和支持向量机回归算法，当选取25棵决策树时，拟合优度达到0.950。随机森林回归算法采取重抽样方法随机有放回地采样，使得随机森林回归算法无需进行太多其他参数的选择，操作简单、泛化能力强、迁移学习能力强，适用于处理训练样本较少带来的模型泛化能力和迁移学习能力不足问题。

4 渗透系数分布特征

利用随机森林回归算法对洪海沟铀矿床西山窑组上段砂体渗透系数进行非线性预测（图4a），砂体渗透系数在平面上分布连续稳定，呈北西-南东向条带状展布，渗透系数在0.20～0.65 m/d 之间变化，砂体渗透性较好，局部呈现渗透系数高值区与低值区。整体上看，砂体厚度大的地区其渗透系数也较高（图4b），比如在K01 勘探线附近砂体厚度在30～45 m 之间，预测渗透系数值在0.30～0.65 m/d 之间，砂体连通性及渗透性均较好，是主河道的发育方向，氧化含矿流体沿主河道方向渗流畅通，在河道前缘及边缘渗流能力渐弱，随着还原物质的增加，铀逐渐“卸载”沉积形成铀矿体。

图4 洪海沟地区西山窑组上段渗透系数（a）及砂体厚度分布图（b）Fig.4 Distribution of permeability coefficient（a）and sand body thickness（b）of the upper member of Xishanyao Formation in Honghaigou area

在垂向上，Ⅰ-Ⅰ’剖面位于河道中心附近，砂体岩性主要为中砂岩及粗砂岩，粒度较大，视电阻率曲线以大型箱型、钟型、漏斗型或其组合叠置型为主，预测其渗透系数在0.35～0.65 m/d 之间（图5），表明砂体内部垂向渗透能力也较强，氧化含矿流体在畅通的砂体内部渗流，在砂体上、下两翼渗透系数逐渐减弱，随着上、下两翼还原物质的增加，铀逐渐“卸载”形成翼部铀矿体。Ⅱ-Ⅱ’剖面位于蚀源区附近，砂体岩性主要为泥岩、细砂岩及中砂岩，粒度较小，视电阻率曲线以箱型、钟型、指型或其组合叠置型为主，预测其渗透系数在0.20～0.38 m/d 之间（图6），表明砂体内部垂向渗透能力较弱，虽然砂体具有一定的厚度，但不利于氧化含矿流体的内部渗流，难以形成较好的铀矿化。

图5 Ⅰ-Ⅰ’剖面渗透系数及铀矿化分布图Fig.5 Relation of permeability coefficient to uranium mineralization in section Ⅰ-Ⅰ’

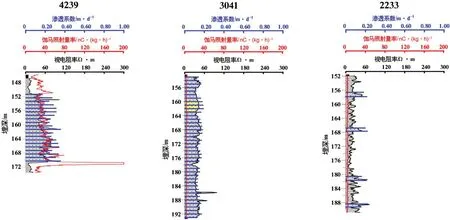
图6 Ⅱ-Ⅱ’剖面渗透系数及铀矿化分布图Fig.6 Relation of permeability coefficient to uranium mineralization in section Ⅱ-Ⅱ’

综上所述，采用随机森林回归算法预测砂体渗透系数，在洪海沟铀矿床取得了较好的应用效果，在平面上砂体渗透系数分布与层间氧化带及铀矿体发育一致，在垂向上砂体渗流能力直接影响翼部矿体形态。基于该方法预测砂体渗透系数，不仅打破了抽水试验试井在空间上分布稀疏的束缚，也避免了因样品分析误差对渗透系数精度的影响。

5 结论

1）本文引入随机森林回归算法通过程序实现了对砂体渗透系数的预测，并将其与非线性回归及支持向量机预测结果进行对比，认为随机森林回归算法具有拟合优度高、操作简单的特点，适用于解决训练样本较少带来的模型泛化能力和迁移学习能力不足问题。

2）将随机森林回归算法应用于洪海沟铀矿床，得到了较好的应用效果，预测砂体渗透系数的空间分布与层间氧化带展布一致，并影响着铀矿体的发育。采用该方法预测砂体渗透系数，不仅打破了抽水试验试井在空间上分布稀疏的束缚，也避免了因样品分析误差对渗透系数精度的影响，具有一定的推广意义和经济价值。

3）从实际应用可以看出，基于机器学习算法并将测井资料与地质资料充分融合，无论是在资料有限的评价区开展探索预测研究，还是在资料丰富的勘探区开展测井精细化评价研究都有重要意义。