一类真菌-浮游动物-浮游植物模型分析
王红月, 赵治涛
(黑龙江大学 数学科学学院, 哈尔滨150080)
0 引 言
水生生态系统是水生生物群落与水环境构成的生态系统,是人类赖以生存的基础资源,在人类的生活环境中占有非常重要的地位。真菌、浮游动物和浮游植物是水生生态系统的重要组成部分,对于维护水生生态系统的可持续发展具有重要作用。研究表明真菌、浮游动物和浮游植物之间存在着复杂的相互作用关系[1-4]。浮游动物捕食浮游植物,并且在这个过程中可能被真菌所感染[5]。真菌以游动孢子的形式存在于水中。真菌孢子通常会附在浮游植物上,或在浮游植物附近,随着水中湍流的作用做随机运动[2,6]。当浮游动物捕食浮游植物时,可能会误食真菌孢子,从而被真菌所感染[2,6]。浮游动物感染真菌孢子会导致其繁殖能力下降,引起浮游动物生物量的减少,甚至灭绝,这可能进一步诱发浮游植物水华,严重威胁着水生生态系统的健康发展。因此,建立数学模型来描述真菌、浮游动物和浮游植物之间的相互作用关系,给出真菌在浮游动物之间传播的阈值条件,刻画真菌对水生生态系统的危害,具有重要的理论价值和实际应用价值[7]。
2015年,Strauss等考虑了一类真菌、浮游动物和浮游植物相互作用模型,并阐明了稀释效应对于真菌传播的影响[8]。2018年,Shocket等指出了温度对于真菌在浮游动物之间传播的作用和影响[2,6]。上述的研究工作中,学者们都假定浮游动物对于浮游植物的捕食关系是线性的。然而,在实际中这种捕食关系通常是非线性的,并且这种非线性捕食关系会引起更加复杂的动力学行为[9-11]。浮游动物感染真菌会导致其生殖能力下降,进而引起浮游动物生物量降低,从而诱发浮游植物水华现象[12]。浮游植物水华是淡水水体中浮游植物大量繁殖的一种生态现象,严重地威胁着水生生态系统的持续发展。在以往的研究中,并没有对这方面的影响进行探究[13-16]。本文将探究浮游动物感染真菌后诱发浮游植物水华的可能性,进一步阐明真菌在浮游动物之间传播的危害。
基于上面的研究动机和以往的研究工作,主要考虑具有Holling II型功能性反应的真菌-浮游动物-浮游植物模型:
(1)
式中:S表示易感的浮游动物;I表示感染的浮游动物;F表示游动的真菌孢子;P表示浮游植物;e表示浮游动物的营养转换效率;a表示浮游动物的觅食率;β表示浮游动物的感染率;γ表示易感的浮游动物的死亡率;δ表示感染的浮游动物的死亡率且δ>γ;σ表示最大的真菌孢子产量;h和ρ表示半饱和系数;μ表示游动孢子的损失率;r表示浮游植物的内禀增长率;θ表示感染浮游动物的繁殖率;K表示浮游植物的最大环境容纳量。对比以往的研究工作,模型(1)考虑了浮游动物对浮游植物的非线性捕食aF(S+I)/(h+F),并同时加入了浮游动物感染真菌后对其繁殖能力的影响因子θ。
本文主要研究系统(1)的动力学性质。首先讨论系统(1)的耗散性,然后分析系统(1)边界平衡点的存在性、局部渐近稳定性和全局渐近稳定性,以及正平衡点的存在性。通过数值模拟验证所得理论结果的有效性。在结论中,指出本文结果所蕴含的生态学意义。
1 系统的耗散性
定理1模型(1)解的全局吸引域为:
这说明模型(1)的解是耗散的。
证明由模型(1)的第四个方程知:
根据微分方程的比较定理有:
模型(1)的第四个方程两边同时乘以e,再与第一个方程和第二个方程相加可得
再利用比较定理可得:
根据模型(1)的第三个方程,对于充分大的t可得:
于是有
这说明区域Δ是模型(1)的全局吸引域,且解是耗散的。
2 平衡点的存在性与稳定性
这部分将研究模型(1)平衡点的存在性及稳定性。模型(1)有如下平衡点:E1=(0,0,0,K),E2=(S2,0,0,P2)和E3=(S3,I3,F3,P3),其中S2和P2满足:
(2)
S3、I3、F3和P3满足:
(3)
定理2E1总是存在的。若γ>eaK/(h+K),则E1=(0,0,0,K)是全局渐近稳定的。
证明E1显然是存在的。模型(1)在E1处的Jacobian矩阵为:
其中
经直接计算可得J(E1)的特征值为λ1=eaK/(h+K)-γ,λ2=-δ,λ3=-μ,λ4=-r。于是,若γ>eaK/(h+K),那么E1是局部渐近稳定的。
下面证明E1的全局渐近稳定性。由系统(1)的前两个方程可以推出对于充分大的t,有
因而,若γ>eaK/(h+K),则
根据渐近自治系统理论[7]知,系统(1)可化简为极限系统:
(4)
显然有
这表明E1是全局吸引的,因而是全局渐近稳定的。
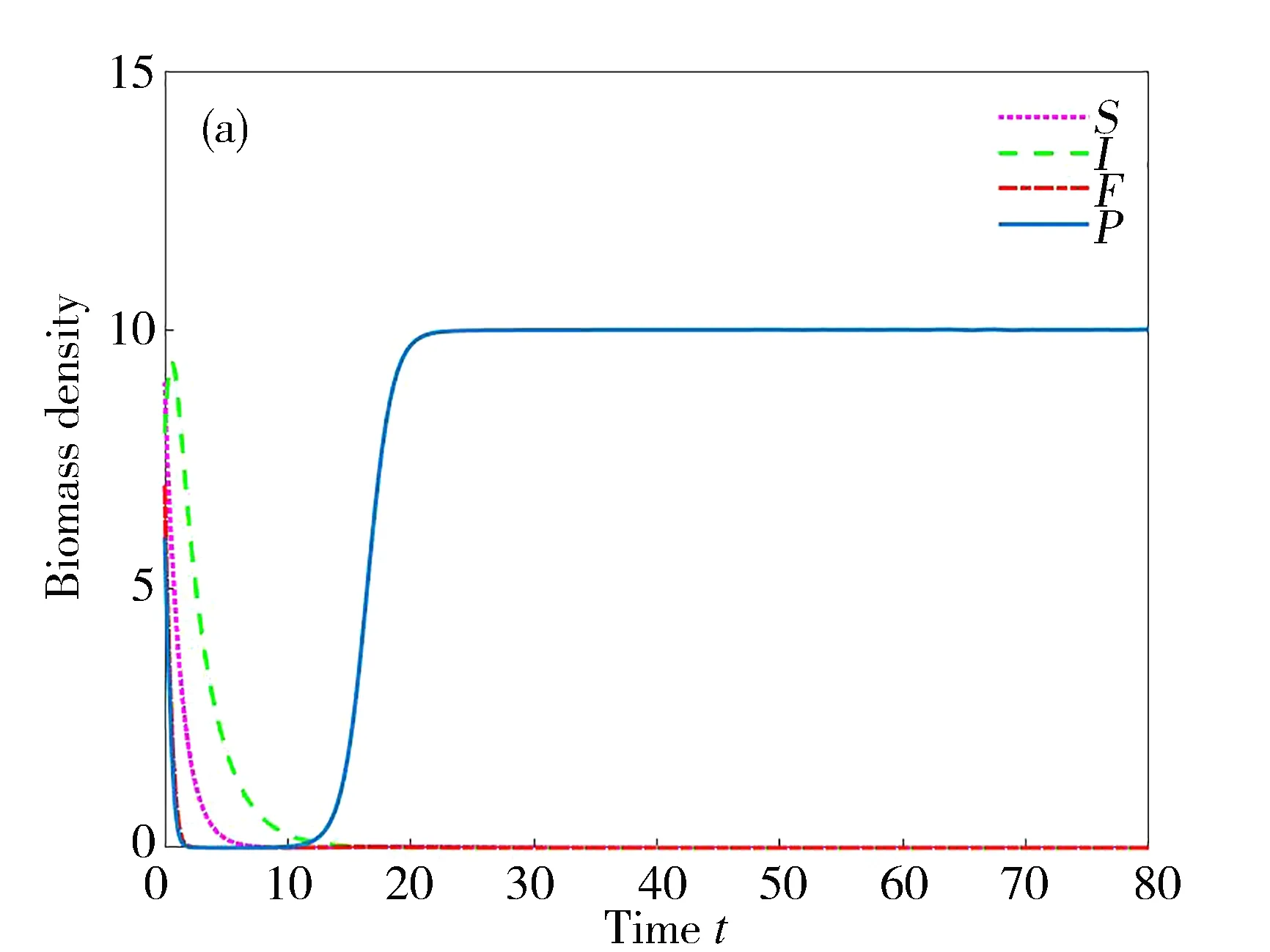
定理3若γ 则E2是局部渐近稳定的。此外,当K=K*时,系统在S-P平面上发生Hopf分支。 证明通过方程(2)直接计算得: 若γ 在E2处的Jacobian矩阵为: 其中 经计算,J(E2)的特征方程为: [λ2-(a22+a33)λ+(a22a33-a32a23)][λ2-a44λ-a14a41]=0 注意到 a22+a33<0,a14a41<0 恒成立。于是,当K 可得J(E2)的特征根均具有负实部,因此E2是局部渐近稳定的。考虑特征方程 λ2-T(K)λ+D(K)=0 定理4若K (1) 模型(1)至少存在一个正平衡点E3; (2) 存在Ω的一个连通子集Ω+使得Ω+连接Γ1,其闭包包含分支点(μ*,S2,0,0,P2),同时在(μ*,S2,0,0,P2)附近,Ω+是一条光滑曲线且对于某个充分小的η>0,满足 证明定义一个映射G:R+×R4→R4为: 其中 (5) 如果(ξ1,ξ2,ξ3,ξ4)∈kerH,则 H1(ξ2,ξ3,ξ4)=0,H2(ξ2,ξ3)=H3(ξ2,ξ3)=0,H4(ξ1,ξ2,ξ4)=0 这说明codim rangeH=1。另一方面, 由Crandall-Rabinowitz分支定理(文献[15]定理1.7)知,存在一个η>0,使所有在(μ*,S2,0,0,P2)附近的正平衡点都位于一条光滑的曲线 其中 由文献[17]中定理3.3和注3.4知,存在Ω的一个连通分支Ω+,它连接Γ1,并且其闭包包含(μ*,S2,0,0,P2),这意味着结论(2)成立。 下面证明结论(1)成立。再次利用文献[18]中定理3.3和注3.4,Ω+满足如下三种情况之一: (1)Ω+在R4中不紧; 在R4中的闭补。 若情况(2)成立,则存在一个正平衡点序列{(μn,Sn,In,Fn,Pn)}满足 (μn,Sn,In,Fn,Pn)→(μ**,S2,0,0,P2),n→∞ 由式(3)的第二个和第三个方程可得: 令n→∞,那么得到 从而有μ**=μ*,此为矛盾。 于是情况(1)必然发生,即Ω+在R4中不紧。由方程(3)可以推出μ>μ*时,模型(1)没有正平衡点。对于μ∈(0,μ*),有 因此Ω+在μ轴投影包含(0,μ*),这说明结论(1)成立。 在本节中,利用Matlab进行数值模拟,来说明模型(1)具有复杂的动力学性质。 令e=0.9,a=0.9,r=1,β=1.35,δ=0.4,ρ=2,θ=0.1,h=2,σ=1.8,μ=0.54。 取γ=0.8,K=10,则γ>eaK/(h+K),于是定理2条件成立。图1(a)显示,仅有浮游植物可以生存,并且达到最大环境容纳量,这意味着平衡点E1存在并稳定;取γ=0.35,K=4,则γ 图1 模型(1)的解收敛于平衡点Ei(i=1,2,3)或者周期解 真菌、浮游动物和浮游植物是水生生态系统的基础,对于维持水生生态系统的健康发展至关重要。本研究表明,若γ>eaK/(h+K)成立,则浮游动物的灭绝是不可避免的,这对于保护水生生态系统的生物多样性是不利的(见定理2和图1(a))。这意味着γ=eaK/(h+K)是浮游动物入侵水生生态系统的一个阈值。若μ>μ*,K 对于所研究模型(1)的动力学性质,建立了浮游动物入侵水生生态系统和真菌在浮游动物之间传播的关键阈值。这两个阈值对维持水生生态系统健康发展至关重要。然而,还有一些理论问题值得进一步探究,如正平衡点的稳定性和Hopf分支的存在性等。在生态方面,还需考虑一些非生物因子,如光照、温度和盐度等,以及生物因子,如鱼类等对真菌-浮游动物-浮游植物相互作用模型的影响。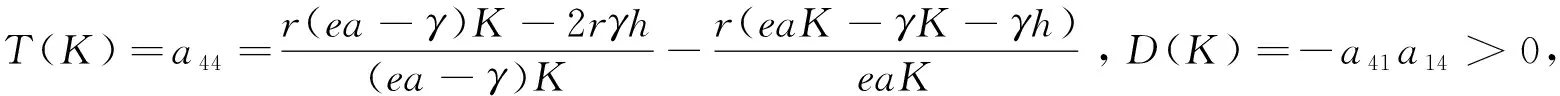

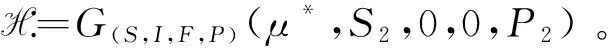



3 数值模拟
4 结 论

