结合深度知识追踪与矩阵补全的习题推荐方法

郭英清,王 敏,2,肖明胜

(1.赣南师范大学 数学与计算机科学学院,江西 赣州 341000;2.江西省数值模拟与仿真技术重点实验室,江西 赣州 341000)

0 引 言

随着教育资源规模日益增大,学习者难以在数量庞大的教学资源中找到符合自身需求的资源。同样地,教师面对大量的学习者也难以做到为每一位学习者提供个性化学习推荐。特别地,在信息过载的今天,为满足不同认知能力和知识水平的学习者需求,如何在大量的习题中精准地推荐合适的习题是个性化学习研究的一项重要课题。

近年来,许多研究者将推荐技术用于习题推荐,其主要思路是以学习者的习题成绩作为评分,将习题得分预测转换成评分预测,从而实现习题推荐。现有的习题推荐方法主要分为基于协同过滤的方法和基于认知诊断的方法。基于协同过滤的习题推荐方法有:Linden等人[1]根据学生做题记录计算相似性得到相似用户,利用相似用户的习题得分预测目标学生得分情况,再用预测结果进行习题推荐。Wu等人[2]结合时间效应提出张量因子分解方法,用矩阵分解方法预测学生习题成绩并依此进行学习资源推荐。Toledo等人[3]在编程平台使用协同过滤方法实现学生的在线习题推荐。周亚[4]将学习者分为新老用户,以协同过滤算法为基础,提出一种混合推荐方法来提高习题推荐效果。蒋昌猛等人[5]通过更新学生-知识点失分率矩阵,获取薄弱知识点并以此进行习题推荐。马骁睿等人[6]用深度知识追踪得到的知识水平矩阵代替交互矩阵,融合相似用户的知识水平向量,得到的推荐结果准确性高、解释性好。基于协同过滤的习题推荐算法简单易部署,但仅参考学习者的答题记录来进行推荐,忽略了学习者的知识水平;另外,协同过滤推荐算法未考虑其他因素对学习者答题情况的影响,推荐结果不具备较好的解释性。

认知诊断方法通过不同的模型对学习者进行能力建模,所得到的参数具有较强的解释性意义,并用于学习者得分预测和试题推荐[7]。Lord[8]提出了项目反应理论(Item Response Theory,IRT),IRT通过模型函数从学习者的作答数据中得到习题参数和学习者能力值,根据习题参数和学习者能力值来进行习题推荐。Corbett等人[9]于1995年提出贝叶斯知识追踪(Bayesian Knowledge Tracing,BKT),将学习者对每个知识点的掌握情况建模为一组二元变量,每个变量代表学习者是否掌握某个知识点,采用隐马尔可夫模型(Hidden Markov Model,HMM)跟踪学生知识状态的变化,预测学生掌握知识点的概率。加性因子模型(Additive Factor Model,AFM)[10]考虑练习尝试次数和学习率两个变量对学习者知识状态的影响,假设学习是一个渐进的变化过程而不是离散的过渡,直接预测学习者正确回答练习的概率。同时,诸多研究者从参数约束[11]、引入失误因子[12]和情绪态度[13]等不同角度对标准AFM进行扩展。基于认知诊断的习题推荐方法考虑到学习者的知识水平,并基于目标的知识水平向量进行推荐。但传统认知诊断方法的数据集需要专家标注,且没有考虑到学习的群体性。认知诊断推荐方法针对学习者个人知识水平建模,在面对知识点和习题一对一关系时,无法推荐学习者未做过的习题,推荐结果存在流行度长尾问题。

综上所述,习题推荐算法主流分为协同过滤和认知诊断方法,但在实际场景下,协同过滤算法忽略了学习者知识水平,仅靠做题记录来进行推荐。认知诊断方法需专家标注数据集,没有考虑到学习的群体性,且大部分推荐算法存在数据稀疏和冷启动问题,难以满足习题推荐需求。因此,如何在数据稀疏情况下对学习者知识状态建模,进而进行习题推荐仍是一个值得研究的问题。

针对上述问题,该文提出一种结合深度知识追踪与矩阵补全的习题推荐方法,命名为DKT-SVD++(Deep Knowledge Tracing based Singular Value Decomposition Plus Plus)。DKT-SVD++用深度知识追踪模型训练得到学习者的知识水平矩阵,又利用奇异值分解模型对未做习题进行评分预测,并对学习者的知识水平矩阵进行补全,进而根据概率高低进行习题推荐。DKT-SVD++由One-Hot编码、知识追踪、知识融合、知识补全和习题推荐五个步骤构成。DKT-SVD++方法具有以下优点:

(1)通过深度知识追踪来获取学习者的知识掌握水平,实现对学习者知识水平的精准建模,推荐结果具有更高精确度。

(2)使用奇异值分解模型对学习者知识矩阵进行补全,缓解了数据稀疏问题,且提高推荐结果的多样性。

(3)DKT-SVD++缓解了依据答题记录进行推荐方法存在的问题,是否答题以及答题正确与否不能代表学习者的知识掌握水平。

DKT-SVD++在KDDCup2010和Statics2011两个公开数据集上与UserCF、DKT和DKT-CF方法进行了性能比较,实验结果验证了DKT-SVD++方法的有效性。

1 相关工作

1.1 知识追踪

知识追踪基于学习者行为序列进行建模,预测学习者知识点的掌握程度,已被广泛应用于智能教学系统中评估学习者的知识水平[14]。知识追踪问题可以描述为:给定一学习者的学习序列x1,x2,…,xt,预测其下次表现xt+1。Corbett等人[9]在1995年提出BKT模型,用二元变量来对学习者的知识点掌握情况进行建模,采用HMM模型来跟踪学生知识状态的变化,预测学生掌握知识点的概率。BKT方法的预测结果具有统计学意义,可解释性较好。然而BKT对于学习的假设具有先天的局限性,使得模型的实际应用范围受限。随后,Kaser等人[15]基于BKT模型,结合习题与知识点中丰富的关联关系提出了约束参数空间的BKT模型,通过实验证明了所提方法在五个大规模数据集中的预测精度更高。Qiu等人[16]在BKT模型中加入知识遗忘特性,模拟学生的知识熟练程度可能随时间的推移而下降。2015年,Chris等人[17]提出深度知识追踪(Deep Knowledge Tracing,DKT)模型,将循环神经网络应用到知识追踪任务中,证明深度知识追踪在不需要专家注释的情况下取得了更好的效果。随后,很多学者对DKT模型进行改进和扩展,以进一步提高预测性能。Dong等人[18]在深度知识追踪中引入注意力机制,在模型中使用Jaccard系数来计算知识点之间的注意力权重,再结合长短期记忆网络与注意力值得到预测结果。Zhang等人[19]提出动态键值存储网络模型(Dynamic Key-Value Memory Networks,DKVMN),将学习者的学习过程建模为读和写两个过程,使用矩阵来存储知识点和知识的掌握程度,再用注意力机制来得到题目和知识点之间相关性,以此来对深度知识追踪模型的可解释性问题进行改进。Lee等人[20]用向量点积来模拟知识状态和知识点的相互作用,用向量来表示学习者对知识点的掌握情况,使得自解释模型(Knowledge Query Network,KQN)具有解释性和直观性。Yeung等人[21]结合了IRT理论和DKVMN模型,提出深度项目反应理论模型(Deep Item Response Theory,Deep-IRT),利用DKVMN对学习者能力和题目难度进行建模,通过IRT得到预测结果。

1.2 知识矩阵补全

通过DKT模型得到的知识水平矩阵存在大量未评分的知识点,为了使得推荐结果尽可能准确,应对原始知识水平矩阵进行补全,再进行习题推荐。在实际情况中评分矩阵往往是稀疏的,为此需要对稀疏的评分矩阵进行补全。常用的方法有矩阵补全、矩阵分解和聚类算法等[22]。矩阵补全方法容易造成补全数据和实际评分偏离程度较大,而聚类需要人为指定聚类个数K,K值会很大程度影响聚类效果[23]。因此,该文采用矩阵分解方法对稀疏知识矩阵进行补全。

矩阵分解是将矩阵拆解为数个矩阵的乘积,常见的有三角分解法、正交三角分解法和奇异值分解法(Singular Value Decomposition,SVD)。SVD作为一种有效的代数特征提取方法,被广泛应用于提取评分矩阵的隐藏特征,进而进行推荐。SVD将评分矩阵分解为两个低阶矩阵的乘积,因此,通过训练得到这两个低阶矩阵可以重构出评分矩阵。为了缓解计算复杂度和数据稀疏带来的问题,Simon Funk[24]提出了隐因子模型(Latent Factor Model,LFM),将评分矩阵优化为两个低秩的用户与项目矩阵。随着LFM的提出,后续又涌现出大量基于LFM的推荐模型。其中,Koren[25]为解决用户评分受用户本身特质的影响,提出了带有三项偏移偏的LFM模型。除了显式的评分行为以外,用户的隐式反馈也可以侧面反映用户的偏好,基于这种假设,Koren[26]提出考虑领域影响的隐语义模型(Singular Value Decomposition Plus Plus,SVD++),缓解了因显式评分过少而引起的冷启动问题;同年,又基于SVD++模型提出了引入时间效应的隐因子模型,通过衰减过往用户行为权重,提高就近用户隐式反馈行为权重来实现动态推荐[27]。在推荐领域,许多研究者结合矩阵分解对推荐方法进行改进。武聪等人[28]通过将标签相似度和用户相似度融入矩阵分解模型中,在提高准确性的同时加强了推荐依据。田震等人[29]在广义矩阵分解的基础上引入隐藏层,利用深层神经网络来学习用户和物品间高阶交互关系,提高推荐结果的准确度。王丹等人[30]将三种不同权重因素融入低秩概率矩阵分解模型中,将特征映射到低秩空间,在正则化约束下对评分进行预测。查琇山等人[31]通过对手游标签聚类求得相似评分矩阵,先使用SVD方法训练得到预测评分,再进行手游推荐。

2 DKT-SVD++习题推荐方法

DKT-SVD++方法首先通过深度知识追踪对学习者的知识掌握情况进行建模,再用SVD++方法预测学习者未做题目的答对概率。DKT-SVD++习题推荐方法不仅利用了学习者自身的知识掌握信息,还考虑到学习者相似群体的知识水平掌握情况,更为重要的是通过SVD++对未做习题进行了预测评分补全。因此,DKT-SVD++方法提高了习题推荐结果的新颖度和精确度。同时,由于采用了SVD++对知识矩阵补全,DKT-SVD++一定程度上缓解了习题推荐系统中的数据稀疏和冷启动问题。

DKT-SVD++方法整体框架:

DKT-SVD++方法整体框架如图1所示,推荐过程分为One-Hot编码、知识追踪、知识融合、知识补全和习题推荐五个步骤,具体如下:

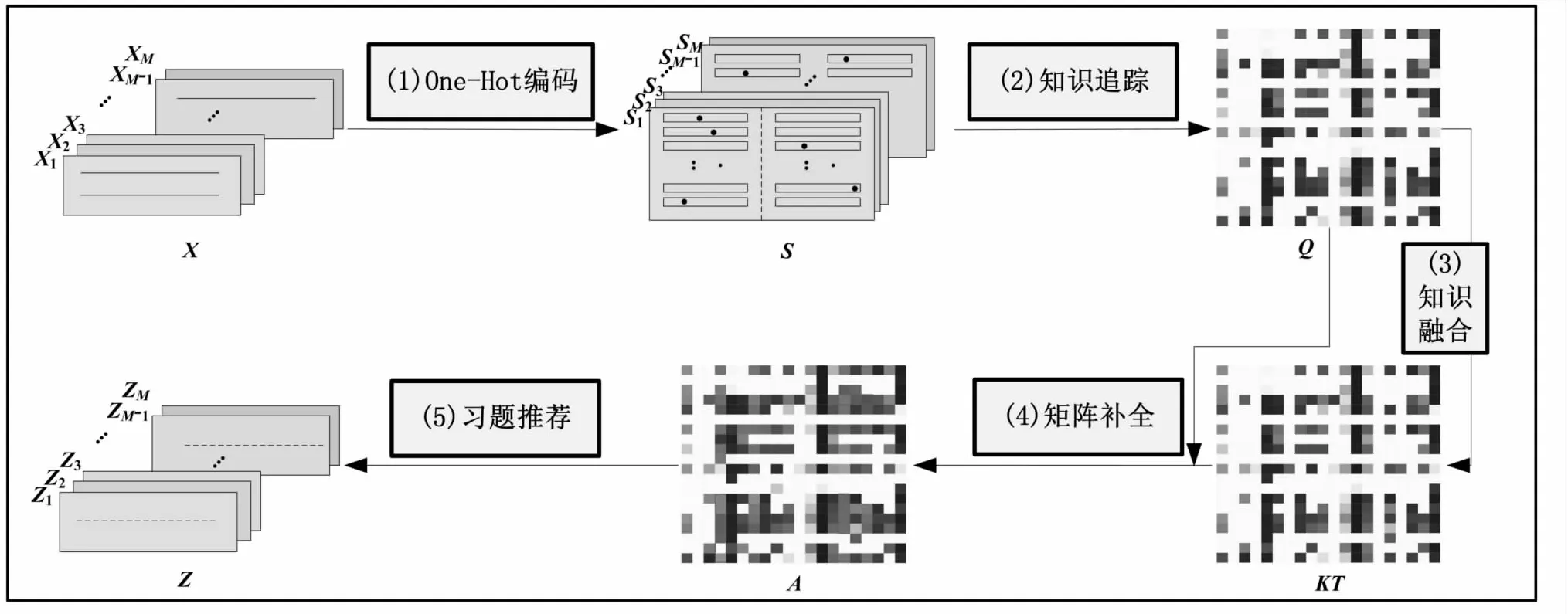
图1 DKT-SVD++框架

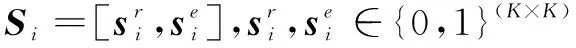
(2)知识追踪:深度知识追踪模型以第i个学习者的独热编码Si为输入,输出其做题正确的概率向量Yi=[yi1,yi2,…,yiK]。这里深度知识追踪模型利用LSTM网络,在t时序网络隐含层的状态ht和输出yt的计算如公式(1)和(2)所示。

ht=tanh(Whxst+Whhht-1+bh)

(1)

yt=σ(Wyhht+by)

(2)

其中,Whx为输入权值矩阵,Whh为递归权值矩阵,Wyh为输出权值矩阵。需要注意的是,有的学习者对同一习题可能多次练习,这时只取最后一次习题答对概率。最后,得到学习者的知识水平矩阵Q∈R(M×N)。

(3)知识融合:用余弦相似度衡量学习者之间的相似性,设Qi={qi1,qi2,…,qiN},Qj={qj1,qj2,…,qjN},则Qi和Qj的余弦相似度计算如下:

(3)

这样,根据余弦相似度大于阈值α的规则可以得到第i个学习者的相似用户Ui={ui1,ui2,…,uiL}。通过公式(4)的计算,得到第i个学习者知识水平向量。

KTi=ρ*Qi+(1-ρ)*average(Ui)

(4)

其中,Qi为第i个学习者的知识水平向量, average(Ui)为相似用户知识水平的平均值,ρ为融合比例。最后得到融合后的学习者知识水平矩阵KT∈R(M×N)。

(4)知识补全:融合后的学习者知识水平矩阵KT表达了学习者对知识的掌握程度,更多考虑相似用户的群体信息。但对于学习者未做习题而言,融合后的知识水平往往预估偏差大,不能较好地表示出学习者的真实知识掌握水平。因此,通过SVD++对学习者未做习题进行知识矩阵补全,某种程度上可以更好缓解数据稀疏问题。以学习者的知识水平矩阵Q为输入,利用SVD++对Q矩阵进行分解(Usvd,Isvd)=SVD(Q)。通过Usvd和Isvd计算出学习者未作答习题的概率,这个概率替换矩阵KT相应位置的概率,从而达到知识矩阵补全的目的。最后得到补全后的知识水平矩阵A。

(5)习题推荐:确定习题推荐个数R和习题难度范围[β1,β2](β1<β2),根据补全后的知识水平矩阵A向学习者推荐答题概率在β1和β2的R道习题。考虑第i个学习者的习题推荐,首先对Ai=[pi1,pi2,…,

算法1:DKT-SVD++习题推荐算法。

输入:学习者答题序列X,难度范围[β1,β2],知识点融合比例ρ,推荐习题个数R。

输出:推荐习题集合Z。

(1)S=onehot(X) //将输入进行One-Hot编码

(2)Q=DKT(S) //训练深度知识追踪模型,构建知识水平矩阵Q

(3)forQi∈Q

forQj∈Q

userCosi,j=cos(Qi,Qj) //计算相似度

(4)Ui=userCosrank(userCosi) //根据排名得到相似用户

(5)KTi=ρ*Qi+(1-ρ)*average(Ui) //更新知识点矩阵KT

(6)fori,j∈KT

KTi,j=SVDpredict(i,j)*average(KTi) //知识点矩阵KT补全

(7)forAi∈A

Zi=recommend(A,ρ,β1,β2,R) //产生学习者i的推荐习题

(8)returnZ//返回推荐习题集合

3 实验与结果

3.1 数据集

实验采用了两组数据集,第一组为KDDCup2010公开数据集,该数据集来自KDD2010年教育数据挖掘大赛的挑战数据集,包含3 310名学生和942 666个答题记录,只保留有知识成分的步骤。第二组为Statics2011数据集,此数据集由工程静态力学课程提供,包含来自333名学生的189 927个记录。两组数据集的相关信息如表1所示.

表1 数据集信息

3.2 评价指标

为衡量提出的DKT-SVD++方法的有效性,实验采用精确率、召回率和F1值作为指标,并与对比方法进行比较。精确率、召回率和F1值分别用公式(5)～公式(7)计算。

(5)

(6)

(7)

其中,TP表示推荐习题中学习者正确回答的个数,FP表示推荐习题中学习者错误回答的个数,FN表示其他待推荐习题中学习者正确回答的数量。

3.3 参考方法

为验证DKT-SVD++方法的习题推荐性能,选择以下三种方法进行比较:

(1)UserCF[32]:使用学习者习题得分矩阵进行基于用户的协同过滤推荐,计算学习者之间的余弦相似度,根据相似学习者的答题情况给目标学习者进行习题推荐。

(2)DKT[17]:根据DKT模型得到学习者知识水平矩阵,给目标学习者知识水平向量进行排名,推荐答对概率最高的习题。

(3)DKT-CF[6]:使用学习者知识水平矩阵进行基于用户的协同过滤推荐,计算学习者之间的余弦相似度,把相似学习者的知识水平向量和目标学习者的知识水平向量进行融合,进而根据概率高低进行排名推荐。

3.4 实验环境与参数设置

实验是在一台配有NVIDIA GTX1050 Ti显卡、16G内存和操作系统为Ubuntu 18.04的台式电脑上进行,编程语言为python3.8,深度学习开发环境为pytorch 1.10.2。

在DKT模型训练阶段,隐含层采用200个LSTM节点,学习率LR设为0.04,训练轮数Epoch设置为500,每批数据大小BATCH_SIZE设为32。KDDCup2010数据集每批最大习题个数MAX_STEP设为1 000,Statics2011数据集每批最大习题个数MAX_STEP设为2 000。

在两个数据集中,均随机划分80%的学习者数据用于训练,20%的学习者数据用于测试。在DKT模型中,只把测试学习者的80%做题记录作为测试,剩下的20%作为未做习题。DKT-CF方法中目标学习者和相似学习者之间知识水平向量的融合比例ρ=0.4。

3.5 性能比较

首先评估SVD++在习题推荐中的性能,然后给出DKT-SVD++与参考方法的性能比较。

(1)SVD++性能评估。

矩阵分解方法采用均方根误差作为评价指标,计算如公式(8)所示:

(8)

在KDDCup2010和Statics2011两个数据集上进行RMSE性能评估。在实验中,兴趣因子Factors设为200,训练轮数Epoch设置为100,学习率LR设为0.005。如图2所示, SVD++均取得了比其他SVD方法更低的RMSE。因此,采用SVD++方法来对知识矩阵进行补全是可行的。

图2 SVD性能比较

(2)性能比较。

表2至表4分别给出了DKT-SVD++与参考方法的精确度、召回率和F1值性能比较。从表中可以看出,基于DKT模型的推荐方法性能均优于UserCF方法。这是因为传统协同过滤方法仅靠答题记录来推荐,这并不能代表学习者对习题所包含知识点的掌握状态,而DKT模型充分利用了学习者知识水平矩阵进行推荐。从表中可以看出,DKT-CF相比与DKT方法,其性能优势很小,这是因为DKT-CF只是利用了相似用户的平均信息。另外,从表中可以看出DKT-SVD++方法性能均优于其他方法,相比其他方法,DKT-SVD++能产生更精准的推荐结果;随着推荐习题数的增加,DKT-SVD++获得越来越大的性能优势。这是因为通过SVD++对学习者知识水平矩阵进行知识补全,充分利用了学习者对未做习题的预测评分。

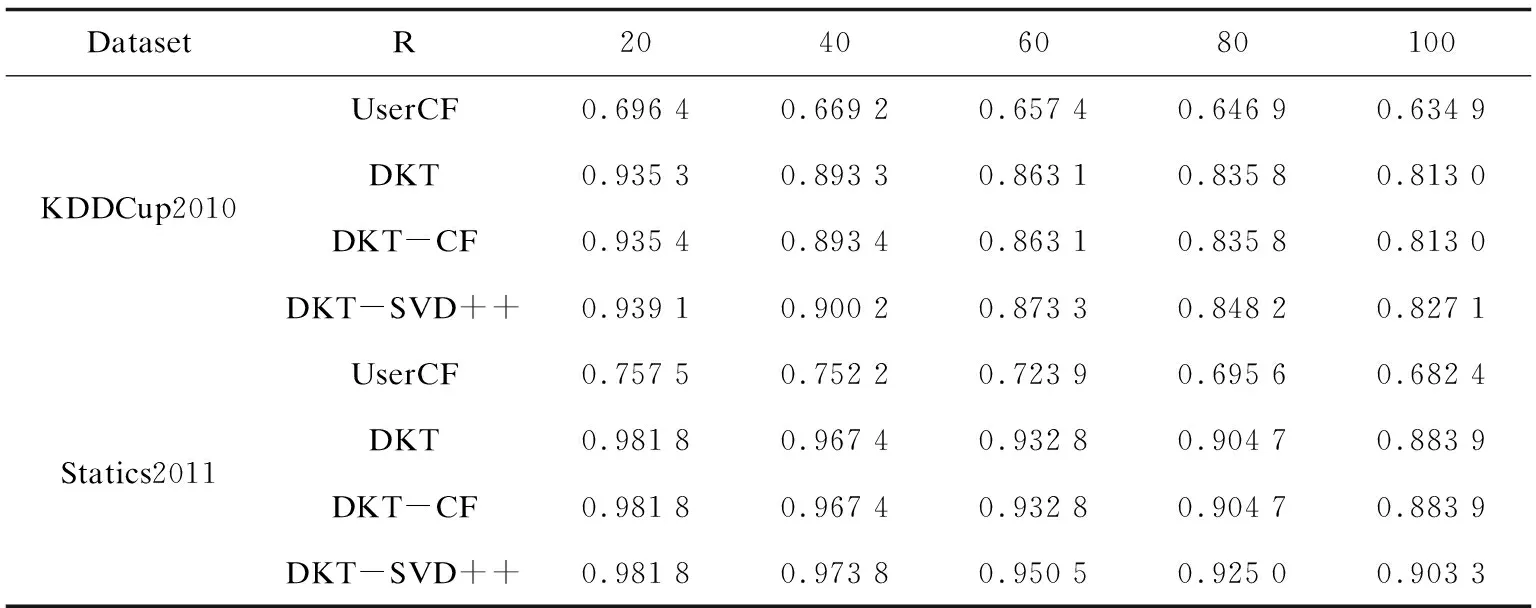
表2 精确度实验结果

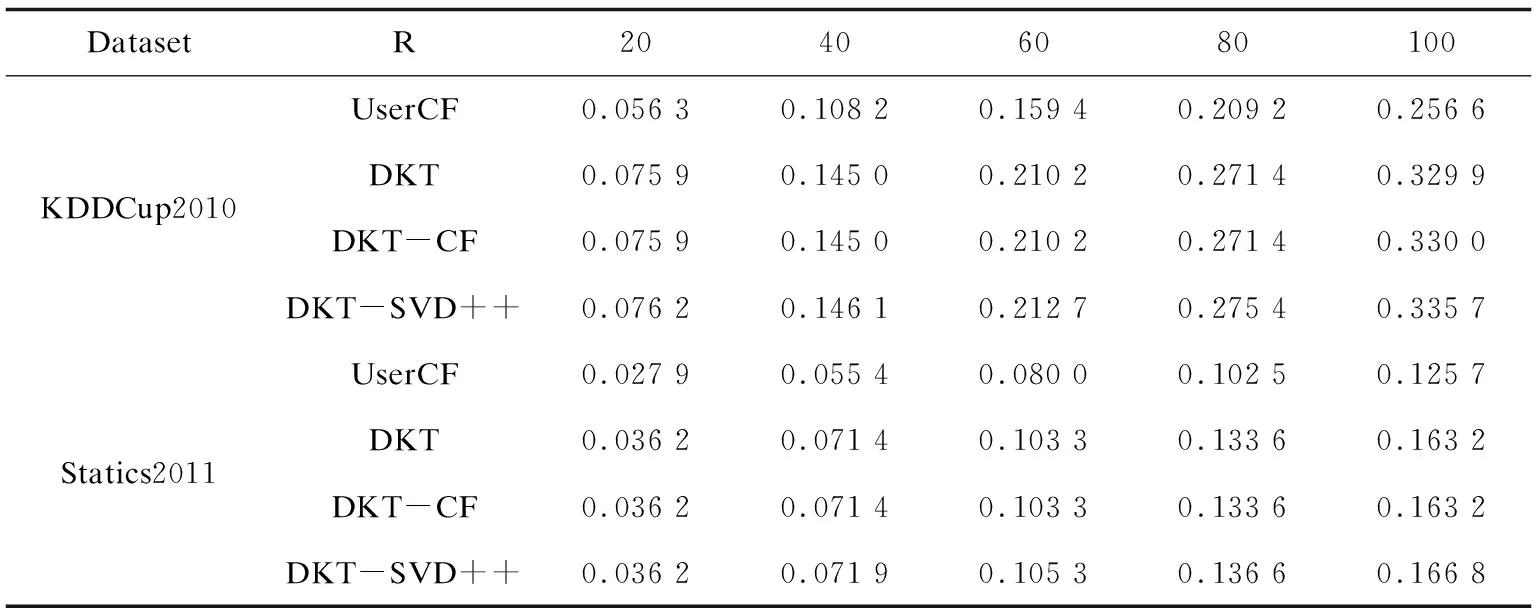
表3 召回率实验结果

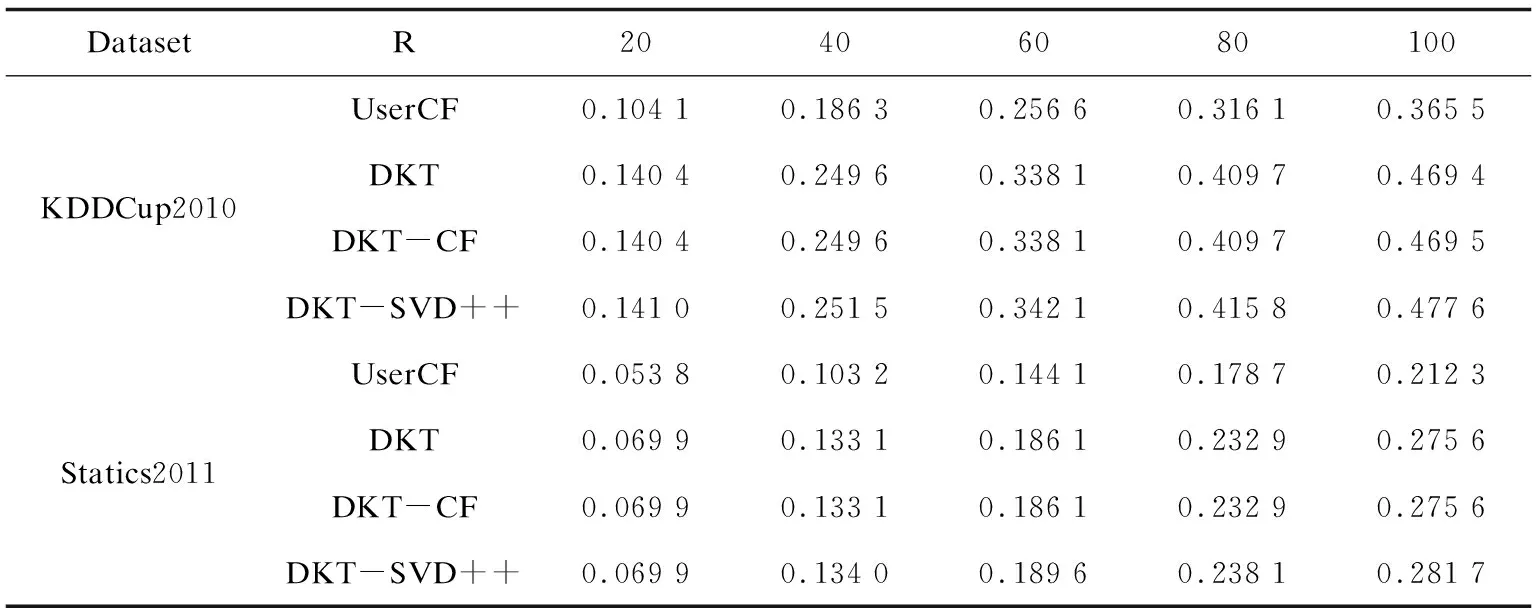
表4 F1值实验结果

(3)消融实验。

为进一步探讨知识融合及稀疏矩阵补全对习题推荐的作用,对所提出的算法框架结构进行了逐层的消融实验。如图1所示,推荐算法框架中三个重要的结构为DKT、知识融合和矩阵补全。根据文献[6]的研究,知识融合比例设置为0.4时算法会有最好的表现和稳定性。因此,在消融实验中,设置知识融合比例ρ=0.4,推荐个数R=100。

分别对基准DKT模型推荐结果,DKT模型融合知识水平向量的推荐结果,DKT模型融合知识水平向量再进行稀疏矩阵补全的推荐结果进行比较,如表5所示。从表中数据可以看出,DKT模型结合知识融合与矩阵补全可以获得最好的推荐性能,这说明在DKT模型基础上,结合知识融合与知识矩阵补全来进行习题推荐是可行的。另外,仅使用DKT模型与知识融合来进行推荐,与基准DKT模型性能相比较,性能增益不明显,这是因为习题推荐未全部命中经知识融合补全后的知识点。知识矩阵补全对推荐结果表现提升明显,这是因为矩阵补全挖掘了用户的潜在特征,可以更好地对学习者进行建模。

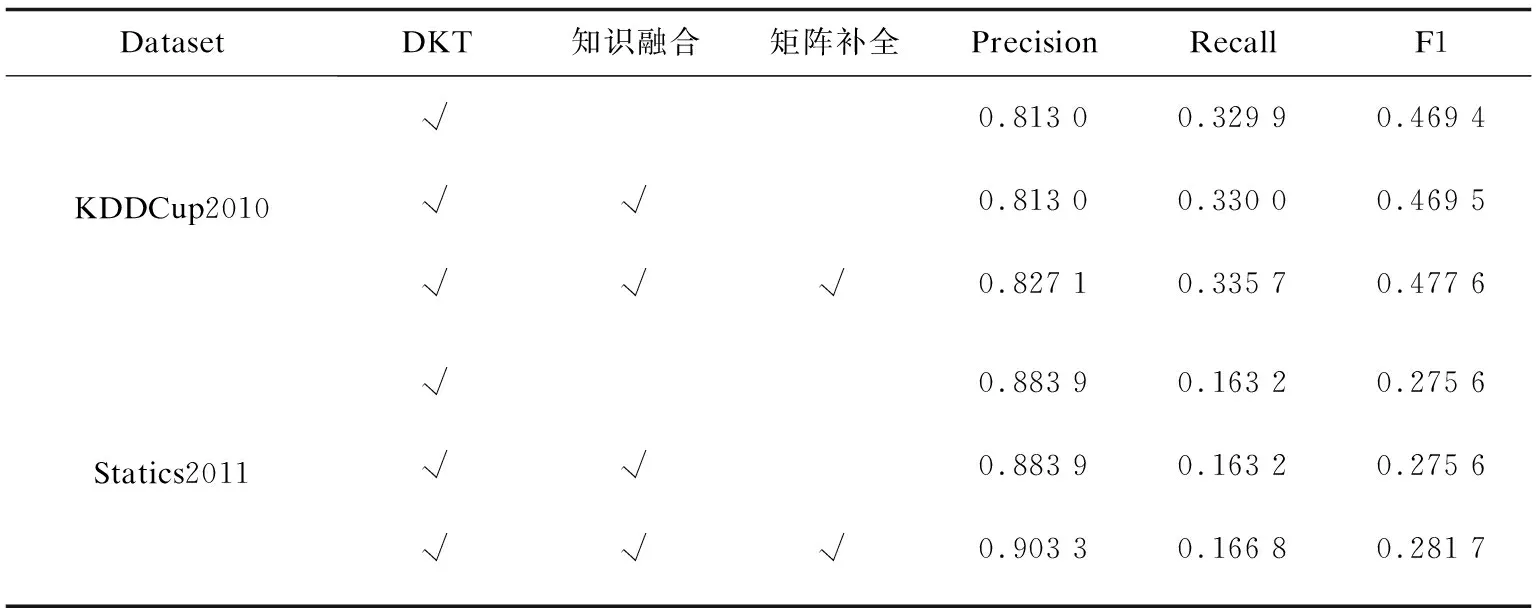
表5 消融实验结果

4 结束语

该文提出一种结合深度知识追踪与矩阵补全的习题推荐方法DKT-SVD++。首先,通过深度知识追踪获得学习者知识水平矩阵,再结合相似学习者信息对知识水平矩阵进行融合,利用矩阵分解方法来进行知识矩阵补全,缓解数据稀疏问题,并依据知识水平矩阵向学习者推荐习题。实验结果表明,DKT-SVD++方法在精确率、召回率和F1值上有明显优势。在后续的研究中,考虑对深度知识追踪模型进行改进,预期学习更多个性化特征;进一步在课程教学的知识图谱基础上对学习者和习题进行建模,从而研究具有更强解释性的推荐方法。