结构化环境下基于点线面特征融合的SLAM算法
曹一波,赵鹏飞,朱海文,刘 顺,张智辉
(华南师范大学 软件学院,广东 佛山 528200)
0 引 言
近年来,视觉同时定位与地图构建(Simultaneous Localization and Mapping,SLAM)技术是计算机视觉和机器人领域的一大研究热点,其核心在于帮助机器人更加准确高效地认知自身位姿和周围环境的几何结构。在基于特征的视觉SLAM中,点特征因其结构简单且容易表达最为常用。典型的点特征方法有PTAM[1]、ORBSLAM[2],通过传统特征检测算法提取图像中的显著角点,再根据角点附近领域信息计算该点的描述子,最后根据数据关联情况构造并求解状态变量。随着近些年深度学习的发展,深度学习以其提取特征更丰富、鲁棒性更强、精度更高和不需要手工设计特征等优点在图像分类、目标检测和图像分割等领域得到了广泛应用[3]。使用深度学习方法进行特征点及描述子的提取也是该领域研究的一大热点问题。如SuperPoint_SLAM[4]使用神经网络提取SuperPoint特征点[5]代替传统手工设计特征,提高了定位的精度和鲁棒性。基于点特征的方法中,特征点在质量上和数量上都对算法的鲁棒性和准确性起着决定性作用。在结构化场景中[6],物体表面、材质性能均一,结构及尺寸变化规律且稳定,多带有显著的几何特征和相对规则的形状,例如墙壁、桌子、门窗和箱子等等。这种场景以低纹理表面为特征的人造环境居多,如走廊、室内停车场等,难以提取到足够多的特征点。为了弥补单一点特征提供特征信息的不足,有学者提出了多种特征相结合的方法,如Pumarola等[7]在ORBSLAM的基础上加入线特征,并提出利用线特征进行系统初始化的方法。Gomez-Ojeda等[8]提出基于双目的点线特征SLAM方法,在回环检测模块中加入并权衡了点线特征。李铁维等[9]采用一种四参数的方式表示空间直线,并使用点线特征联合图优化去估计相机位姿,有效改善了因相机运动过快产生的跟丢问题。Yang Gao等[10]提出的RGB-D相机下基于点线面特征的视觉里程计,定义了一种平面特征的匹配方法及平面特征的误差表示方法。Zhang等[11]提出的室内环境下基于点面的RGB-D SLAM,为平面增加了平行和垂直的约束关系。李海丰等[12]提出的基于点线面特征的PLP-SLAM,其点特征用于对机器人当前位姿进行初始估计,线和平面特征用来描述环境信息,但该方法的本质还是依赖点特征实现定位。线、面特征在结构化环境中较为丰富且对光照变化更加鲁棒,将它们和点特征共同用于SLAM系统中,通过增加特征的数量[13]来提高定位算法的精度。
传统的多种特征结合的方法通过帧间匹配直接计算位姿信息,不可避免地会产生累计误差,从而导致定位不准确[14]。一种策略是加入回环检测和位姿图优化来纠正误差,然而这会带来额外的计算负担。另一种则是根据特殊的场景结构来减少累计误差。在结构化场景中,物体多表现为平面性和正交性,大都满足建立曼哈顿世界[15]的条件,即所处环境由三个正交方向的几何结构组成。由于旋转误差是总误差的主要来源,并且每帧与曼哈顿世界坐标系理论上可以求得无漂移的旋转,从而间接得到帧间的旋转,减少累计旋转误差[16]。Joo等[17]在图像帧中为曼哈顿世界提供了分支定界框架。MVO中[18]提出了一种单位球均值偏移方法,用于寻找曼哈顿世界和相机坐标系之间的旋转矩阵。OPVO中[19]使用平面来估计曼哈顿框架间的旋转,在至少具有两个正交平面的环境中,通过分别估计相机旋转和平移运动实现了准确和低误差的状态估计。Li等[20]提出的RGB-D SLAM系统,结合多种传统几何特征并利用曼哈顿世界假设,该系统有效提高了结构化环境下的定位精度。
综上所述,为了充分利用结构化环境下的多种特征信息,以及基于深度学习提取特征更丰富、鲁棒性更强、精度更高和不需要手工设计特征等优点,提出一种SuperPoint点特征与线面特征融合的SLAM算法。在使用特征数据的策略方面,不直接计算帧间的位姿变换,而是利用线面特征,基于曼哈顿世界假设,估计每帧与曼哈顿世界坐标系的相对旋转来得到帧间旋转,减少了旋转的累计误差,然后通过求解最小化联合点线面的重投影误差函数得到平移。将6自由度位姿解耦为3自由度的旋转和平移,降低了算法对特征信息的依赖同时也减少了计算量。位姿优化方面,根据结构化环境下的特性,添加了平面间的垂直和平行约束关系,并使用关键帧构建的局部地图优化位姿。在TUM公开数据集上与现有的主流方法对比表明,该算法有效提升了结构化低纹理环境下的定位精度。
1 基于点线面特征融合的SLAM算法
1.1 算法流程
算法整体流程如图1所示。
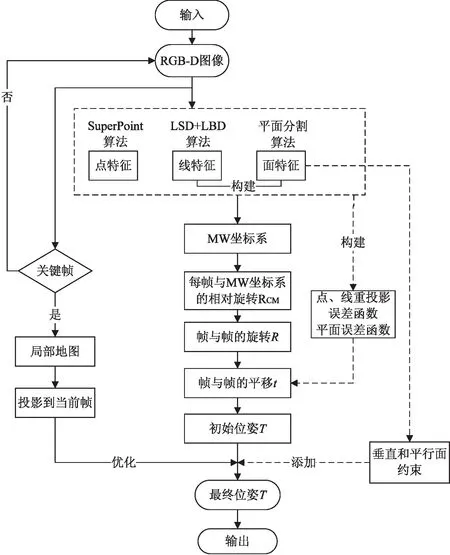
图1 算法整体流程
算法主要以基于深度学习的SuperPoint点特征和传统线、面特征相结合,以及结构化场景特性借助曼哈顿世界假设来提高定位的精度和鲁棒性。算法以RGB-D相机获取的RGB-D图像作为数据来源,通过SuperPoint算法提取点特征,LSD算法[21]提取线特征,使用平面分割算法[22]得到面特征。点、线特征的匹配由SuperPoint描述子之间的距离和LBD描述子之间的距离分别得到,平面特征的匹配通过平面到原点的距离、平面间夹角得到。由图像中提取的线、面构建曼哈顿世界坐标系,通过求每帧与曼哈顿世界坐标系的相对旋转来间接得到帧与帧之间的相对旋转R,然后构建联合点线面的重投影误差函数,代入R并求解此函数即可获得平移t。根据结构化场景下平面间相互垂直和平行的特性添加约束函数优化位姿。同时为弥补环境中出现不严格遵守曼哈顿世界假设的情况,使用关键帧构建的局部地图投影到当前帧进一步优化位姿。
1.2 相关特征的提取与匹配
1.2.1 SuperPoint点特征
SuperPoint是一种先进的用于特征点检测以及计算描述子的自监督框架,由MagicPoint和Homographic两部分组成。前者是用于特征点检测的基于VGG神经网络,后者是用于生成特征点的描述子。SuperPoint对环境光照和视点变化的鲁棒性使其更加稳定,在Hpatches数据集[23]上的性能优于ORB、SIFT等传统手工设计点特征。在SuperPoint_SLAM中,该SLAM系统采用ORBSLAM2[24]的框架,采用SuperPoint点特征替换ORB点特征,其在建筑物多的场景定位表现优于ORBSLAM2。文中算法主要应用在结构化环境下,场景中以人造建筑物居多,使用基于深度学习的SuperPoint点特征与线面特征相结合能有效提高SLAM定位的精度。在得到点特征和其描述子之后,通过计算描述子距离完成点特征之间的匹配。在提取图像中的二维点特征后,利用相机内参和深度图将其反向投影,获得对应三维空间点。结构化纹理环境下提取的SuperPoint点特征如图2所示。

图2 结构化纹理环境下提取的SuperPoint点特征
1.2.2 线特征和面特征
结构化场景中,常常存在低纹理表面为特征的人造环境,点特征提取不到或数量太少不足以成功跟踪位姿,所以算法中加入了直线和平面特征。线特征使用LSD算法从图像中拟合得到,使用LBD算法得到线特征的描述子,根据描述子距离完成线特征之间的匹配。和点特征一样,经过反投影后得到三维线。但由于RGB-D相机得到的深度图在物体边界处会出现深度不连续的先天性弱势,势必会存在由于深度错误导致投影的不准确情况,为克服这种情况的影响,该文对3D线进行滤波,即通过RANSAC的方法对线段上的外点进行剔除。
RGB-D图像能够提供有序的点云[25],使用算法[22]从点云中分割并提取平面特征。其中平面由hassion的参数方程来表示,记作π=(nT,d),其中n=(nx,ny,nz)T是平面的单位法向量,d(d>0)是相机原点到该平面的距离。平面检测之后,使用文献[10]中的数据关联方法进行平面匹配,即两平面法向量夹角小于10度、原点到平面距离d之差小于0.1米。此外,还将探索局部地图中的平面和当前帧中检测到的平面之间的关系,以在优化位姿时增加额外的约束。结构化低纹理环境下提取的线、面特征如图3所示。

图3 结构化低纹理环境下提取的线、面特征
1.3 位姿估计
1.3.1 基于曼哈顿世界假设的旋转估计
当提取到线面特征后,根据结构化环境下的正交特性,利用文献[20]中的方法可将环境建模为曼哈顿世界,通过球面均值漂移法来估计每帧与曼哈顿坐标系之间的旋转关系RCM[18],如图4所示。其中,C0、Ck、Ck+1是初始时刻以及第k和k+1时相机的位姿,其与曼哈顿坐标系的旋转关系分别为RC0M、RCKM、RCK+1M。

图4 基于曼哈顿世界坐标系的旋转估计
在上述得到第k和k+1帧与曼哈顿坐标系之间的相对旋转关系后,根据公式(1),就可以估计出k到k+1帧的旋转RCK+1CK。
RCK+1CK=RCK+1MRCKMT
(1)
根据世界坐标系与曼哈顿坐标系之间的旋转关系RMW,由公式(2),就可以得到每一时刻相机与世界坐标系下的旋转情况。
RCkW=RCkMRMW
(2)
其中,RMW由曼哈顿世界初始化时得到。
通过借助曼哈顿世界假设将位姿解耦,可单独求解3自由度的旋转,不仅减少了计算量,而且旋转估计不会受到上一帧或参考帧姿态的影响,误差将不会累计,有效降低了旋转累计误差。
1.3.2 平移估计
在完成位姿的旋转估计后,通过最小化联合点线面的重投影误差函数来估计位姿中剩余的3自由度平移。首先,将匹配好的参考帧中的三维点重新投影到当前帧中[26],构建关于点的重投影误差函数:
(3)
其中,Π(.)为投影函数,Pj是参考帧中的三维点,pk是当前帧的像素坐标,Rk,j是参考帧到当前帧的旋转矩阵并在上节方法中已经得到,只需求解参考帧到当前帧的平移矩阵tk,j即可。对于线,使用端点pstart和pend来获得归一化的线段,其描述如下所示:
(4)
然后,通过参考帧中的线段端点到当前帧直线的距离来定义线的重投影误差函数[27-28],误差函数可以表示为:
(5)
对于平面,为了避免平面表示方法的过参,可将其最小参数化,表示为q(π)=(φ,ψ,d),其中φ和ψ是法线的方位角和仰角。平面表示方法如下:
(6)
因此,参考帧中的平面πj与当前帧中的平面πk之间的误差函数可表示为:
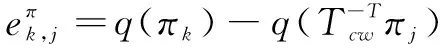
(7)

(8)
其中,∑p-1、∑l-1、∑π-1分别表示点线面特征在第k帧中的协方差矩阵,ρp、ρl、ρπ分别表示联合误差函数中点线面特征对应的鲁棒Huber函数。
最后使用LM(Levenberg-Marquart)算法最小化联合误差函数Et求解得到平移。
1.4 位姿优化
结构化环境下,平面间呈现垂直和平行的关系。利用这一特性,可将地图中的平面和当前帧检测的平面添加垂直和平行的约束,约束函数如下所示:
(9)
(10)
其中,qn(π)=(φ,ψ)。对于互相垂直的平面,将其平面法线旋转90度(R⊥)以构建误差函数,同时这两个误差函数在优化时被合并到(8)中建立联合误差函数。结构化环境下,相机运动到不严格遵守曼哈顿世界的时刻,会使得定位精度下降。因此,该文采用ORBSLAM2的策略选择关键帧并建立含有点、线、面的局部地图,基于局部地图投影到当前帧的策略来优化位姿,提高定位精度。
2 实 验
2.1 实验平台及数据集介绍
实验所用的电脑软硬件配置:CPU为Inter Core i5-9400F,6核处理器,主频2.9 GHz,内存8 GB,GPU为1050Ti,系统为Ubuntu16.04。使用TUM RGB-D公开数据集的四个结构化场景的序列进行实验测试,其中fr3-structure-texture-far、fr3-structure-texture-near为结构化纹理环境,fr3-structure-notexture-far、fr3-structure-notexture-near为结构化低纹理环境,以下简称为st-far、st-near、snot-far和snot-near[29]。
2.2 实验结果与分析
为了验证提出的基于深度学习的SuperPoint点特征与传统线面特征相结合能够有效提升结构化环境下SLAM定位算法的精度,将所提算法与基于ORB点特征的ORBSLAM2、基于SuperPoint点特征的SuperPoint_SLAM[4]、基于传统点面特征的PP_SLAM[11]、基于传统点线面特征的PLANAR_SLAM[20]作对比分析。绝对轨迹误差(Absolute Trajectory Error,ATE)直接计算相机位姿的真实值与SLAM定位算法的估计值之差,代表轨迹的全局一致性,此标准非常适合评估SLAM系统的性能,如式(11):
(11)
其中,Testi,i是估计轨迹,Tgt,i是真实轨迹,i=1,2,…,N。首先单独比较了几种算法在绝对轨迹中的旋转误差。
如图5所示,除st-near序列,所提算法在其他序列上的旋转误差值明显低于对比算法,表明借助曼哈顿世界假设去求解位姿中的旋转能够有效减少旋转的累计误差。

图5 几种算法的旋转误差对比
对于绝对轨迹误差进行分析,就要得到相机传感器在数据集各个序列上的运动轨迹。图6是几种算法在各个序列上的运动轨迹和真实轨迹的对比, 可以看出所提算法在结构化低纹理的环境中比其他算法更贴近于真值,表明所提算法在这些环境下的定位精度更高。表1数据是几种算法绝对轨迹误差的具体数值,代表各算法对相机位姿的估计值与真实值之间的差异,数值越小,算法定位精度越高。从表1数据可知,在snot-far、snot-near序列中,ORBSLAM2和SuperPoint_SLAM过于依赖点特征,在上述序列因点特征提取不到或提取数量过少导致跟踪丢失。所提算法基于点线面多种特征,弥补了单一点特征在低纹理环境下跟踪丢失的问题,并且绝对轨迹误差也保持在较小的水平,表明所提算法在结构化低纹理环境下能够有效提高SLAM的定位精度。在st-far、st-near序列中,点特征比较丰富,且ORBSLAM2、SuperPoint_SLAM、PP_SLAM中含有全局BA模块,使得所提算法在这两个序列中稍逊一筹,但是比之同样没有全局BA模块的PLANAR_SLAM,所提算法的误差更小,也体现了基于SuperPoint点特征与线面特征结合相对于传统点线面特征结合的优势。
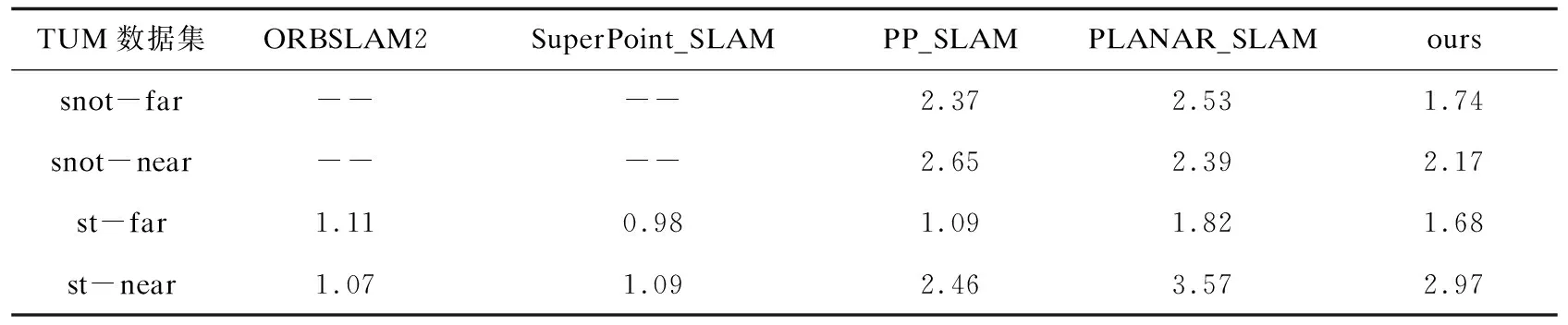
表1 几种算法的绝对轨迹误差对比 cm
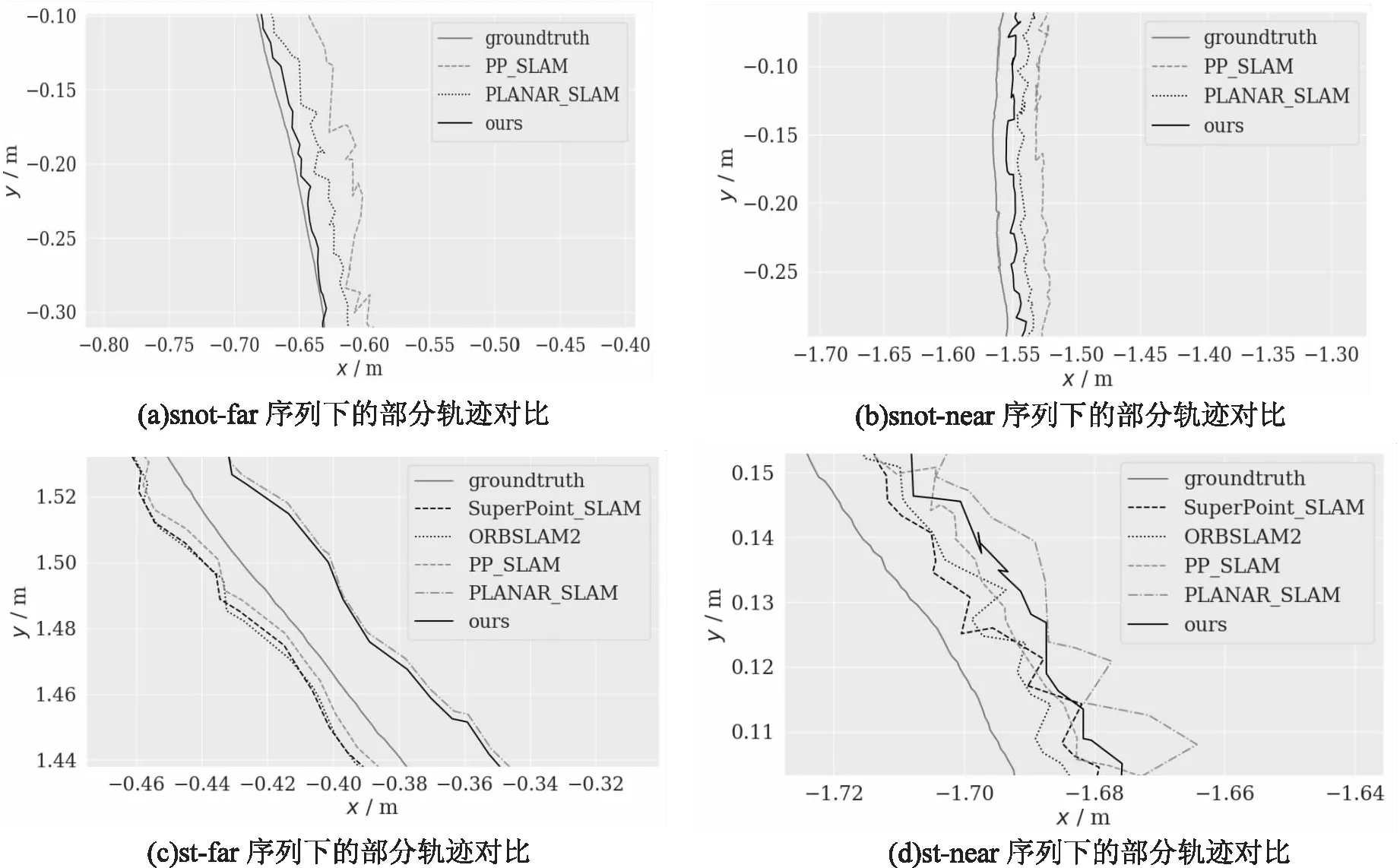
图6 几种算法在TUM数据集序列下的部分轨迹
3 结束语
提出了一种基于点线面特征融合的SLAM定位算法,多种特征相结合充分利用了环境中的特征信息,解决了纯点特征在低纹理环境下跟踪丢失的问题。将基于深度学习的SuperPoint点特征与传统线面特征相结合,利用结构化环境特性,借助曼哈顿世界假设减少了累计误差。实验表明,相较于传统多种特征融合的方法,该算法有效提高了结构化低纹理环境下的定位精度。在未来的研究中,将考虑加入全局位姿优化以及回环检测模块,以进一步提升算法定位的准确性和鲁棒性。

