人口转型与消费结构变迁：理论推演与情景模拟

崔晓东，郑玉华

（1.南京晓庄学院 商学院，南京 210017；2.南京信息工程大学 管理工程学院，南京 210000）

0 引言

消费是经济持续增长的“稳定器”和“压舱石”。凯恩斯消费理论认为消费是收入的增函数，我国居民消费支出随收入的增加而增加也有相关经验佐证。然而近年来，尽管宏观层面国民经济保持稳中向好、稳中有进的发展态势，但收入增长并不像过去一段时期一样明显促进消费[1,2]，正在发生的人口结构转型可能成为消费的重要影响因素。关于人口转型如何影响居民消费，普遍认同的观点是其通过人口抚养比影响收入进而影响消费[3,4]，抚养比下降带来的人口红利对我国经济的高速增长也极具解释力。那么从消费视角可否认为抚养比越小越好？少子化和老龄化同时发生，可否预期二者因对冲而并不会对消费造成大的影响？虽然从总抚养比来看确实产生了一定程度的抵消[5,6]，但只有在二者独立且对消费的影响同质的情况下才可以简单加总。而现实中二者影响未必同质，生命周期理论认为消费者在不同年龄段的消费行为具有显著差异，不加区别地加总模糊了二者的异质性[7]。两者之间存在关联，少子化和老龄化本质上是人口结构转型的起点和归宿，少子化必然导致老龄化，而老龄化会进一步加剧少子化，他们存在互促逻辑。另外，现有研究大多属于经验性验证，对产生逻辑未加推演的验证是缺乏根基的，可能会产生片面化、碎片化或莫衷一是的结论[8,9]。

基于已有研究，本文以人口转型通过抚养比进而影响消费为研究逻辑，构建外生生育率和内生生育率人口结构模型，推演人口结构影响消费的理论逻辑，通过模拟解释和预判人口结构变化引致的消费变迁，从消费视角模拟有效的应对策略。

1 模型构建

1.1 基准模型

假设个体同质生命周期包括少儿期、成年期和老年期三个阶段，将总人口分为少年组、成年组和老年组，PY、PM和PO表示各组人口数量。假设个体按照统一经济生活模式，少儿期依赖父母，成年期参加劳动，老年期退休，少儿抚养比y和老年抚养比o分别为y=PY PM和o=PO PM。

假设各时期长度为TY、TM和TO，少年期进入成年期、成年期进入老年期的概率为λY、λM，老年期的死亡概率为λO，概率用各时期长度的倒数表示。假设死亡只发生在老年期①如果放松死亡仅发生在老年期的假设，就需要在人口流动方程中加入各期的死亡概率，但由于少儿期和成年期死亡人数相对较少，并且在本文的讨论中并不涉及这两项概率，为方便起见进行了省略假设。，新生人口数量为N，则人口流动方程为：

假设成年组中育龄人口比例为φ，n(y，o)为总和生育率，稳定人口结构②稳定人口，即人口年龄结构保持不变增长的人口变动状态。尽管现实中大多数国家的人口变动属于非稳态增长，稳态人口常被作为基准来判断人口年龄结构的动态变化。下的抚养比满足：

式（2）为少儿抚养比y与总和生育率n(y，o)的函数关系，式（3）为老年抚养比o和少儿抚养比y的函数关系，由此建立了稳定人口结构基本模型。

人口转型通常通过人口抚养比影响消费，本文基于同一思路，但在计算抚养负担时考虑到不同年龄群体的异质性[10—12]，对少儿抚养负担和老年抚养负担分别赋权ρY和ρO，并称其为经济抚养指数e(y，o)，e(y，o)=yρY+oρO。当权重ρY和ρO给定时，e(y，o)表现为二维(y，o)平面上一系列平行直线。当人口结构曲线给定时，可以计算任意点处的经济抚养指数，消费作为经济抚养指数的反向变量，进而考察人口结构对消费的影响。

根据式（2），如果生育率n(y，o)为不依赖于模型参数的外生变量，那么稳定人口结构状态下的老年抚养比o和少儿抚养比y就具有明晰的关系式，反之两者关系就比较复杂。接下来根据生育率n(y，o)是否为外生变量分别建立外生生育率和内生生育率稳定人口模型。

1.2 外生生育率人口结构模型

1.2.1 人口结构曲线和消费曲线

外生生育率模型，即式（2）中总和生育率n(y，o)为不依赖于模型中其他参数时的人口结构模型。假设此时生育率为n，根据式（2）可以得出少儿抚养比y，根据式（3）得出老年抚养比o和少儿抚养比y的函数关系。为更直观地进行展示，本文在二维(y，o)平面用稳定人口结构曲线s(y，o)表示二者关系，利用式（3）对y的一阶导和二阶导反映曲线特征：o′= -λmλy·(yλy-λm+λO)-2，o″=2λM λY2(λY y+λO-λM)-3。一阶导o′小于0，二阶导大于0（λO-λM可知s(y，o)为递减的凹函数，如图1 所示，曲线上各点代表稳定人口模型中老年抚养比o和少儿抚养比y的组合，各点处斜率代表二者的边际替代率。

图1 稳态人口结构曲线

经济抚养指数e(y，o)为二维(y，o)平面上一系列平行线，随右上平移经济抚养指数增大，与曲线S(y，o)相切（即S(y，o) 上某点斜率等于e(y，o) 直线斜率时，切点为经济抚养指数最小的抚养比组合，由式（3）可求出切点(y0，o0)位置，如图1 所示。切点(y0，o0)是经济抚养指数最小的点，那么根据图1，稳定人口结构曲线上各点的抚养指数呈先减后增的“U”型曲线，相应地，各点对应的消费（本文称之为潜在消费c(y，o)）以切点为拐点呈先增后降的“倒U”型曲线，如图2所示。

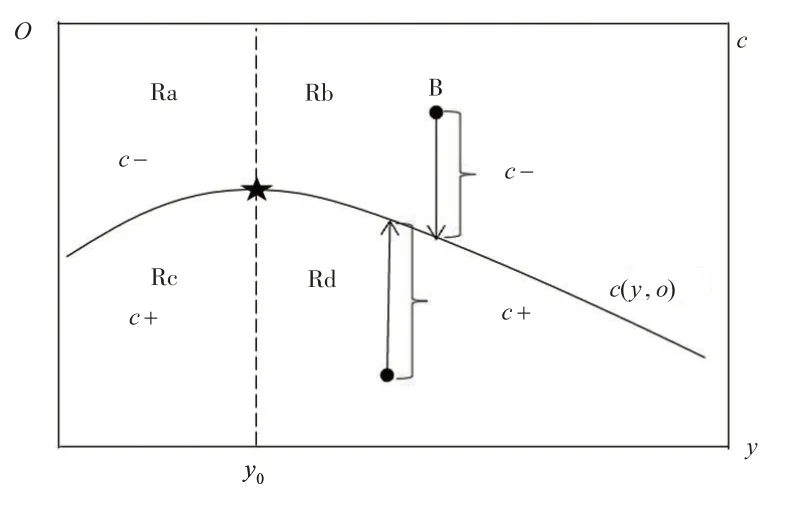
图2 人口结构与潜在消费

潜在消费曲线c(y，o)反映了人口结构变化过程中各个阶段的潜在消费，从右往左看，在人口变化的早期，即高少儿抚养比y（高生育率）和低老年抚养比o（高死亡率）时期，大量的少儿抚养人口使人均收入和消费增长缓慢，随着时间推移，少儿人口形成劳动人口，收入和消费最大限度地提升，之后老年人口比例增加，收入和消费开始下降。

图1以人口结构曲线s(y，o)为界将区域分为上、下两个部分，因为经济抚养指数e(y，o)为一系列右上平行线，所以当其他条件不变时上方区域各点对应的经济抚养指数要大于对应稳定人口曲线上各点的经济抚养指数，下方区域则相反。与此对应，图2 以c(y，o)为界，上方为因经济抚养指数较大导致消费可能较小的区域，下方为经济抚养指数较小导致消费可能较大的区域。仿照人口红利的概念，将下方消费较大的区域称为人口消费红利区（或c+），上方消费较小的区域称为人口消费负利区（或c-）。进一步以消费最大时的直线y=y0为界将区域分为左右两个部分，整个区域包括Ra、Rb、Rc和Rd四个部分，可以根据人口抚养结构所在的区域判断对消费的影响。由此得出：

命题1：稳定人口结构曲线为向下的凹函数，潜在消费曲线呈先增后减的“倒U”型；存在潜在消费最大化的最优人口结构；与稳定人口结构下的潜在消费相比，其他人口结构由于经济抚养指数可能引致消费红利或消费负利。

1.2.2 外生人口结构变动

生育率变动是少儿抚养比变动的根本原因，生育率为外生变量且下降时，将相继引发少儿抚养比减少和老年抚养比增加，由此对消费的影响取决于初始人口结构。如下页图3所示，初始少儿抚养比大于y0即在直线y=y0的右侧时，如点(y1，o1)，生育率下降经由少儿抚养比下降和老年抚养比增加稳定在此时的潜在消费相对于点(y1，o1)增加了Δc；相反，如果初始少儿抚养比小于y0即在直线y=y0左侧，如图3 中点(y2，o2)，生育率下降经由少儿抚养比下降和老年抚养比增加稳定在此时的潜在消费相对于点(y2，o2)减少了Δc。由此得出：

图3 少儿抚养比与潜在消费

命题2：在外生生育率模型下，生育率下降对潜在消费的影响取决于初始人口结构；当初始少儿抚养比大于拐点处少儿抚养比时，生育率下降，潜在消费上升，消费红利增加或消费负利减少；反之，当初始少儿抚养比小于拐点处少儿抚养比时，生育率下降，潜在消费下降，消费红利减少或消费负利增加。

拐点两侧生育率下降引致的消费差异可做如下解释，当初始少儿抚养比位于拐点右侧时，可以看作是以高出生率、高死亡率为特征的人口变化早期阶段，此时由生育率下降导致的少儿抚养比下降并没有使老年抚养比快速上升，最终使经济抚养指数下降、潜在消费增加。相反，初始少儿抚养比在拐点左侧，也就是低生育率阶段，如果生育率继续下降，就将导致老年抚养比增加的速度大于少儿抚养比下降的速度，最终使经济抚养指数上升、潜在消费减少。少儿抚养比和潜在消费的“倒U”型关系与Ronald等（2014）[13]利用40多个国家数据进行的经验验证的结果基本一致。

生育率下降是老龄化的主要原因，寿命延长具有放大老龄化的作用。根据式（2）和式（3），当其他参数不变时，寿命延长表现为老年抚养比的增加，但并不影响其他年龄段人口占比，因此寿命延长后的稳态人口曲线表现为向上平移，总经济抚养指数相应增大、潜在消费相应变小(c(y，o)→c′(y，o))。同时经济抚养指数直线与稳态人口曲线相切时的最优人口结构点向右上方平移((y0，o0)→(y′0，最低经济抚养指数增大、最大潜在消费下降，如图4所示。由此得出：

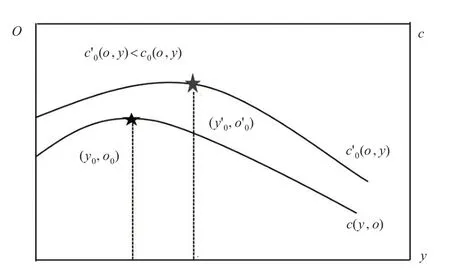
图4 老年抚养比与潜在消费

命题3：在外生生育率模型下，当其他条件不变时，寿命延长导致稳态人口曲线向上平移，经济抚养指数增大、潜在消费变小；相应地，可能的消费红利减少或消费负利增加。

1.3 内生生育率人口结构

1.3.1 内生人口结构方程

上文假设生育率是与模型其他变量无关的外生变量，但实际上在引起生育率下降的众多原因中，由老年抚养比上升引起的养老负担增加对生育偏好产生的挤出也不能忽视，因此，将生育数量作为个体效用最大化目标下的结果更接近现实，本文考察内生人口结构模型下的消费。

宏观经济表现通常为微观个体行为的放大与总和，在此先讨论个体最优生育决策。假设同上文一致，个体生命周期包括少儿期、成年期和老年期三个阶段，少儿期不参与劳动，成年期参与劳动获得收入W，同时社保缴费率τ用于老年期的转移支付，假设社会保障制度为现收现付制，η为养老金平均工资替代率，则养老保险基金预算平衡方程为PMW=PM(1-τ)W+PO(1-τ)Wη，据此可得1-

假设成年期生育子女数量为n，每个孩子的养育成本占工资的比例为ς，θ为育儿偏好，采用对数效用函数，成年期效用函数①为讨论方便并突出重点，本文省略了虽然看起来完善但不影响结论的变量，比如老年期效用、老年期消费等，而仅考虑与生育率有关的成年期效用。为：

效用最大化目标下的最优生育数量为：

显然最优生育数量是育儿偏好的增函数，是生育成本反函数。将最优生育数量n代入式（2）和式（3），可得稳态人口结构曲线：

观察式（6）和式（7），y和o相互嵌套，很难得到如外生模型中的明晰解，也很难画出二者的曲线图，但可以根据因果逻辑进行序贯分析。

1.3.2 内生人口结构变动

考察生育率下降引起的一系列反映：当生育数量下降（n↓）时，根据式（1）可知少儿抚养比下降（y↓），根据式（7）可知老年抚养比上升（o↑），进而根据式（5）发现生育数量进一步下降（n↓），如此进入下一个循环（可简化为n↓→y↓→o↑→n↓→…），直到两次生育数量足够靠近为止。显然每循环一次，老年抚养比进一步增加，生育数量进一步下降，因此和外生生育率模型只发生一次冲击相比，内生生育率下降后的稳定点将产生更大的移动，即图3 中的继续向左上（或左下）方偏移，如此一来少儿抚养比和老年抚养比的边际替代率更大，人口结构曲线更加陡峭。

考察预期寿命延长情况：显然当其他条件不变时，预期寿命延长使老年抚养比上升（o↑），代入式（5）可知生育数量下降，少儿抚养比变低（y↓），根据式（7），老年抚养比上升（o↑），进入下一个循环（可以简化为z↑→o↑→n↓→y↓→o↑→…），直到两次老年抚养比足够接近为止。同样地，与外生生育模型寿命延长时人口曲线仅向上平移相比，此时的人口曲线将更大幅度地同时向上和向左平移。由此得出：

命题4：内生生育率模型下的人口结构曲线比外生人口结构曲线更陡峭；生育率下降或寿命延长对潜在消费、消费红利或消费负利的影响方向与外生生育率模型一致，但影响幅度更大。

2 数据模拟

本文基于以上方程，通过数据模拟对2000—2020 年的消费事实进行解释，并对2021—2035年的消费趋势进行预判，同时也对可能的生育鼓励政策的调节效应进行模拟。

本文之所以选择2000—2020 年为经验事实模拟期，是因为此时间段是我国人口结构转型和人口红利变迁的典型时期，包括劳动人口数量达峰、劳动人口占比下降、生育政策调整等重要时间节点，具有典型代表性和重要性。之所以选择2021—2035 年为预判模拟期，是因为该时间段既是我国人口年龄结构加速转型的阶段，也是积极应对人口老龄化以实现“十四五”规划与2035年远景目标的关键时期。模型参数设定包括：按研究惯例，将生命周期划分为三个时期：15岁以下为少儿期，15～65岁为成年期，65岁以上为老年期，期限长度分别为15、50和T－65，T为预期寿命，假定退出各期的概率分别为期限长度的倒数，即0.067，0.02 和1/(T-65)；消费权重根据我国各年龄段人口消费特征并结合希纳等学者对消费人口赋权的原则，以成年期消费为基准，将其设为1，少年期权重为0.65，老年期权重为1.35。实际上本文也进行了稳健性检验，包括增加或降低相对比重，发现未影响整体变化趋势和特征。

2.1 经验事实：2000—2020年的人口结构与消费

利用2000—2021年《中国统计年鉴》人口年龄结构数据，结合消费权重计算经济抚养指数，并根据外生生育率模型计算潜在经济抚养指数，潜在经济抚养指数与实际经济抚养指数之差即从抚养角度由人口结构引致的抚养红利，或从消费视角的消费红利，观察两者差异变化特征来解释消费变迁事实。选择外生生育率模型的原因在于我国2000—2020 年的大部分时间内仍是一孩生育政策，2016年和2019年的生育政策虽有调整但因时间短而对生育选择的影响有限。

图5 反映了2000—2020 年实际经济抚养指数和潜在经济抚养指数的关系及变迁。可以看出，自2000年以来，实际经济抚养指数先缓慢平稳下降而后相对快速上升，其中2010 年为方向拐点，这与我国劳动年龄人口在2010 年到达峰值继而向下、拐点前少儿抚养比下降但老年抚养比并未快速上升有关。与之不同，潜在经济抚养指数除了个别年份有波动外基本呈平缓增长趋势，且始终处于实际经济抚养指数曲线之上。消费作为经济抚养指数的反向指标，图6 显示了潜在消费、实际消费及消费红利的关系①在进行数据模拟时为保证消费为正数，在模型中加入了常数项。因此本文模拟的只能是变化趋势或特征，着重强调的是人口结构与消费、实际消费和潜在消费之间的关系，而非绝对量的大小。，潜在经济抚养指数和实际经济抚养指数之差即从人口抚养角度获得的消费红利，图中圆点代表消费红利的大小。可以看出，实际消费和消费红利在此期间先后经历由增到减的变化，实际消费以2010年为拐点，消费红利在2014年达峰后进入下行区间，但到2020年并未出现明显式微或者关闭。与Cai 和Lu（2013）[14]估算的人口红利于2010 年开始下降并逐渐式微的结论相比，本文的消费红利达峰时间相对滞后且持续存在。

图5 2000—2020实际经济抚养指数和潜在经济抚养指数

图6 2000—2020年潜在消费、实际消费和消费红利

2.2 模拟预测：2021—2035年的人口结构与消费

本文利用内生生育率模型模拟2021—2035年人口结构变迁和消费的关系。选择内生生育率模型的原因如前文所述，我国生育政策放开、个体或家庭可以在效用最大化目标下选择生育数量。根据式（4）至式（6），模拟所需参数除上文的人口参数外，还包括未来人口结构变化参数，本文借鉴联合国发布的《世界人口展望2019》及相关文献，以2020年数据为基准，假设2021—2035年老年人口比重增长率为0.0371，少儿人口比重增长率为-0.0125，养老金平均工资替代率η以0.6 作为基准值，并取0.5 和0.7 进行敏感性测试[15]。为方便起见，将式（4）育儿偏好和育儿负担参数组合统称为育儿偏好，其值根据2020年的人口统计数据计算，2020年总和生育率为1.3，老年抚养比为0.197，养老金平均工资替代率η为0.6，根据式（4）可得为1.45。同时本文借鉴已有文献[16]进行校准，子女数量偏好θ为0.9～1.2，反推生育成本ς为0.31～0.36。育龄人数占比φ，同样以2020年人口统计数据作为校准，2020 年总和生育率为1.3，出生率为8.52‰，根据出生率*总人口＝总和生育率*育龄人口占劳动人口比例*劳动人口，即可得育龄人口占劳动人口比例φ为9.55‰。

结合以上参数，先模拟少儿抚养比下降和老年抚养比上升两种情况下的潜在消费，按以下序贯过程，根据预期的少儿抚养比，计算与此对应的稳定人口结构下的老年抚养比，并计算老年抚养比下的生育数量，再计算与此对应的少儿抚养比，如此循环，直到最终趋于稳定（本文在相邻两次老年抚养比相差小于1‰时终止迭代）。老年抚养比上升时的模拟与此类似，区别在于最初设定的是老年抚养比预期，然后计算对应的生育数量，再计算少儿抚养比，继而计算老年抚养比，如此循环迭代。模拟结果如图7所示。

图7 两种情景下2021—2035年的潜在消费

可以发现，两种情景下的潜在消费在模拟区间都呈下降趋势，对比来看，少儿抚养比下降时的潜在消费曲线始终位于老年抚养比上升时的潜在消费曲线之下，但二者差距渐趋缩小，说明在其他条件相同时，少儿抚养比下降对消费的冲击要大于老年抚养比上升的冲击，其原因在于少儿抚养比下降引致老年抚养比上升的幅度要超过老年抚养比上升引致少儿抚养比下降的幅度。不过随着预期寿命持续延长，两种效应之差渐趋减弱，实际上按既定假设模拟至2040年时两者已经非常接近。

本文分别模拟了少儿抚养比下降和老年抚养比上升时的潜在消费，以此可对比两者消费效应的大小，但实际上未来的人口变化是两种情景叠加，需要综合结果才能表现未来的消费情况。鉴于两种效应是相互影响的序贯动态过程，很难将两种情形放在同一场景中模拟，因此本文采用类似全微分方法①全微分要求变量之间相互独立，但内生生育率模型假设少儿抚养比和老年抚养比存在关联，因此此处的计算方法只能是类似全微分。，分别求出两种效应后按年份取平均，结果如图8 所示。可以看出，可能消费和潜在消费两种曲线都呈下降趋势，说明从人口转型视角来看，未来消费水平不可避免地下降，但可能消费曲线始终位于潜在消费曲线之上，说明消费红利虽不大但依然存在，不过仍可看出其逐渐减少趋势，实际上按设定的人口转型速度，模拟显示消费红利将在2037年式微乃至消失。本文模拟的消费红利消失时间要晚于蔡昉（2021）[17]的研究结果（由人口抚养比带来的人口红利将在2030年进入尾声），其原因可做两方面解释，一是本文的模拟并未考虑未来育龄人群的规模及比例的减少，这可能会低估生育数量的递减速度；二是判断红利是否消失的参照标准不同，本文区别于绝对人口抚养比，是以稳定人口结构下的人口抚养比为标准，通过对比预期人口抚养比和稳定人口结构下抚养比的差异来判断。

图8 2020—2035年潜在消费、预期消费和预期消费红利

2.3 稳健性检验

本文进行了三项稳健性检验：一是改变老年抚养比和少儿抚养比的消费权重，分别在10%范围内扩大和缩小两者比重，结果发现模拟的绝对值大小会有波动但并不影响前文方向性结论。二是降低育儿成本和养老金替代率的稳健性检验，这两项也是从消费视角对鼓励生育政策的检验。假设育儿成本由政府承担其中10%，大致相当于13个月的带薪育儿假，系数校准为1.667，结果发现未来潜在消费仍不可避免地下降。养老金工资替代率下降为0.5时模拟结果与图7无太大差异。三是育儿成本下降及养老金平均工资替代率同时下降的情况，如图9 所示，模拟区间内预期消费仍然高于潜在消费，消费红利持续存在，同时与图8（相对较高的育儿成本和养老金平均工资替代率）相比，潜在消费和预期消费两曲线距离较大，即鼓励生育组合政策能够扩大消费红利。

图9 稳健性检验

3 结论与展望

本文以人口转型通过抚养比进而影响消费为研究逻辑，基于稳定人口方程，首先构建外生生育率和内生生育率人口结构模型，结合经济抚养指数曲线，讨论少儿抚养比和老年抚养比变化影响消费的理论逻辑，然后基于该逻辑对2000—2020年人口转型引发消费红利的经典事实进行模拟，最后对2021—2035 年可能的消费结构变迁进行预判。研究发现，人口转型对消费的影响方向并不存在必然的或正或负的结论，而是取决于初始人口结构。我国在过去的二十多年人口结构处于消费红利区，但红利规模在2014 年达到峰值后开始下降；按照《世界人口展望2019》预测的我国人口转型速度，到2035 年消费水平从人口结构视角来看无可避免地整体下降，消费红利虽式微但仍存在。相对而言，互促逻辑使得少儿抚养比下降对消费的负向影响要大于老年抚养比的影响，降低养育成本、提高生育偏好对少儿抚养比下降的负向影响具有一定对冲作用，但降低养老金工资替代率的功效不大。在老龄化加剧的情景下，优化生育支持体系、抑制生育率下降可以在一定程度上阻滞消费继续下滑。如此，推动经济增长扩大消费贡献度的政策措施要基于人口结构导致消费水平客观下降的背景事实，加快建立扩大消费需求长效机制，释放居民消费潜力，从影响和制约消费水平的因素出发寻求提升建议。

人口老龄化既是我国乃至世界长期面临的大趋势，也是影响各国经济增长的宏大背景。本文从理论逻辑到现实模拟讨论人口转型如何作用于消费变迁，丰富和补充了既有经验研究的相关文献。尽管如此，本文仍属于静态的程式化研究，存在一定的局限，未来可以拓展的方向包括细分年龄组尤其是老年人这个异质性非常大的群体，不同群体在消费上可能存在较大的差异，或是人口负增长背景下的人口和消费，也可以将生育数量最优决策单位由个人转为家庭、消费由数量扩展为结构等。