基于卡尔曼滤波算法改进的宏观经济实时预测方法与实证

张居营，张 镝，赵宣凯

（1.河北金融学院 金融与投资学院，河北 保定 071051；2.中信建投证券股份有限公司，北京 100010；3.中央财经大学a.经济学院；b.中国互联网经济研究院，北京 100081）

0 引言

宏观经济预测对政府、企业、居民等部门具有重要的信号指示作用，有助于及时决策，更好地进行经济预判和防范风险。但数据采集和整理需要时间，数据发布往往具有滞后性，例如我国年度、季度GDP 数据通常滞后一个多月发布，现实情况突发变化可能导致决策陷入被动。近年来，由于受到全球竞争格局重塑、地缘冲突加剧以及重大公共卫生事件等一系列因素的影响，各国经济波动愈加剧烈，趋势反转概率加大，促使决策者更加注重宏观经济预判，以提前布局、制定合理决策来化解风险，这便产生了实时预测（Nowcasting）的方法。目前，实时预测仍面临两大障碍：一是数据统计方面，宏观经济变量门类众多，项目繁杂，且方法不断更新，统计指标与统计口径纷繁复杂，频率各不相同，时常面临日、周、旬、月、季度、年度等混频数据问题，且存在数据缺失问题，如何高质量地从多维数据中提取有效信息，并进行精准、及时预测是一大难题；二是预测方法方面，采用单一指标的预测方法，如ARMA、GARCH 等容纳的信息量相对有限，预测的波动性较大，采用多指标预测方法中以VAR 为代表的传统模型存在“维度诅咒”问题，变量个数较多时参数难以估计，而采用稀疏建模的高维数据处理方法筛选部分变量参与预测的过程中必定会损失一部分信息，同时对于混频数据缺失值过多的问题也缺少合理办法进行有效填补，导致其使用存在限制。

动态因子模型在一定程度上能解决上述问题，它将宏观变量视为“公共因子”和“特质扰动项”两个部分，通过信息组合和噪声过滤，提取主要因素，在假设宏观经济不同部门的波动是由若干“公共因子”共同驱动的条件下，对相应变量进行预测[1]。动态因子模型可以表示为状态空间的形式，应用卡尔曼滤波构造似然函数，并用极大似然估计法来估计参数，从而处理不规则混频数据，但是估计过程中会用到非线性的数值优化算法，对高维度的数据处理能力有限。后期Stock 和Watson（2002）[2]、Forni 等（2005）[3]通过放松假定条件，在允许特质扰动项满足一定条件时应用主成分分析法提取因子。Doz等（2011）[4]进一步应用卡尔曼滤波算法对主成分估计的各因子初始值进行修正，得到了较为稳健而准确的因子估计值，形成了卡尔曼滤波算法两步估计框架。目前动态因子模型的实时预测得到广泛应用，刘汉和刘金全（2011）[5]对我国季度GDP 进行实时预测，取得了较好的预测效果，Allan 等（2014）[6]用实时预测方法估计了部分数据没有专门发布的苏格兰的GDP 增长，为地区经济实时预报提供了借鉴。

基于动态因子模型的实时预测方法虽然能够解决混频数据发布不同步、数据缺失的问题，但是，在不确定性冲击下，宏观预测仍存在效果不佳、时滞性等问题，如不确定性冲击导致经济先下降再回升的“V”型反转加大了实时预测难度[7]。尚泰等（2016）[8]提出了基于卡尔曼滤波的三阶段固定区间平滑算法，指出该算法能够循环多次使用卡尔曼滤波,提高估计精度，并在初始状态未知的情况下具有较强应用价值，但是该方面尚未应用到宏观经济实时预测方法中。鉴于此，本文在动态因子模型实时预测的参数估计中改进卡尔曼滤波的固定区间平滑算法，引入再次前向滤波平滑过程的三阶段算法，探讨其预测效果，并验证改进算法是否能够更有效地利用先验信息，提升预测精度，在经济运行非常规状态下是否也能快速响应，改善预测时滞性问题。

1 模型构建

1.1 动态因子模型

动态因子模型假设n个变量在t期的观测向量yt=(yi，t，…，yn，t)T可以由r个难以观测到的动态公共因子向量ft=(fi，t，…，fr，t)T以及特异因子et=( ei，t，…，en，t)T来描述，形式如下：式（1）为测量方程，描述了数据yt和动态因子ft之间的关系，其中C 为n×r 的因子载荷矩阵（通常r ≪n）。ft、et分别为不同变量序列之间的共同成分、特异成分，并且假定et～N(0，R)。 R 是测量噪声协方差，实际操作中一般可以观测到，是滤波器的已知条件。式（2）为转移方程，假定隐含的动态因子向量服从VAR(1)过程，A 为r×r 的VAR 过程转移稀疏矩阵。 μt为r 维列向量且μt～N(0，Q)。式（1）和式（2）共同构成了一个状态空间模型，ft、et都是未观测到的状态。通过计算主成分初始化模型的待估参数，将主成分视为真正的公共因子。用yt对ft的初始估计值做最小二乘回归，即可得到C 的初始估计和et向量，计算et的协方差矩阵即得到R 的初始估计。将ft的协方差矩阵记为P ，根据ft的初始值计算出P 的初始估计。

1.2 卡尔曼滤波平滑算法的使用与改进

在得到所有未知参数的初始估计后，就可以使用基于卡尔曼滤波的两阶段固定区间平滑算法进行参数估计和数据更新，主要分为前向滤波和后向平滑过程。

前向滤波过程将ft与P 的初始估计记为对C 、A、R、Q 分别赋予初始值然后利用t-1 期的数据来预测t 期的参数，这一步对ft与P 的预测结果分别记为，通过计算卡尔曼增益：并设定阈值，来实现对第1期到第t 期的预测更新，从和开始迭代循环得到和，完成前向滤波的过程。后向平滑过程是将正向滤波最后得到的和按时间t 逆向倒推，t 依次取N-1，N-2，…，0，每一步的平滑步骤如下：首先，计算平滑增益矩阵其次，进行平滑估计fs，k=ff，k+Hs，k(fs，k+1-ff，k+1/k)；最后，计算平滑协方差矩阵变量下标f 和s 分别代表该时刻的正向滤波结果和平滑结果。其中，为系统状态转移矩阵。

尚泰等（2016）[8]提出了基于卡尔曼滤波的三阶段固定区间平滑算法，相比两阶段平滑算法，用第二阶段后向平滑过程得到的作为滤波初始值，再次从头到尾处理观测值，并得到最终的状态估计，即为三阶段固定区间平滑估计的输出。与两阶段固定区间平滑算法相比，三阶段算法由于多次使用卡尔曼滤波，理论上使得稳定性获得进一步提升，充分利用了现有数据中公共因子与特异因子信息的先验信息，并做了变化趋势上的再次平滑，因此更接近经济实际运行状态。

2 研究设计

2.1 数据集构建与指标选取

考虑到宏观经济中的统计变量门类的复杂性、变量间信息交叉性，本文在构建数据集时，将宏观经济分为经济运行、景气与信心、工业、投资、消费与价格、劳动力、金融与货币七大门类。不同门类混频指标的选取见下页表1和下文表2，共计81 个指标，其中月度指标66 个，季度指标15 个，时间跨度为2005 年1 月1 日至2022 年11 月31日，数据来自国家统计局官网季度与月度公开数据、CEIC数据库、Wind数据库等。考虑到预测对象的不同，参考唐晓彬等（2022）[9]在对宏观经济进行实时预测时选取的指标，对于季度GDP同比增速的预测，主要从投资、消费、贸易、就业以及相关行业、工业运行、金融状况等方面选取变量；对于月度CPI的预测，主要考虑整体经济运行状况、景气指数、货运物流、消费与价格、金融货币等与价格有关的变量，具体见表1和表2的第5列。

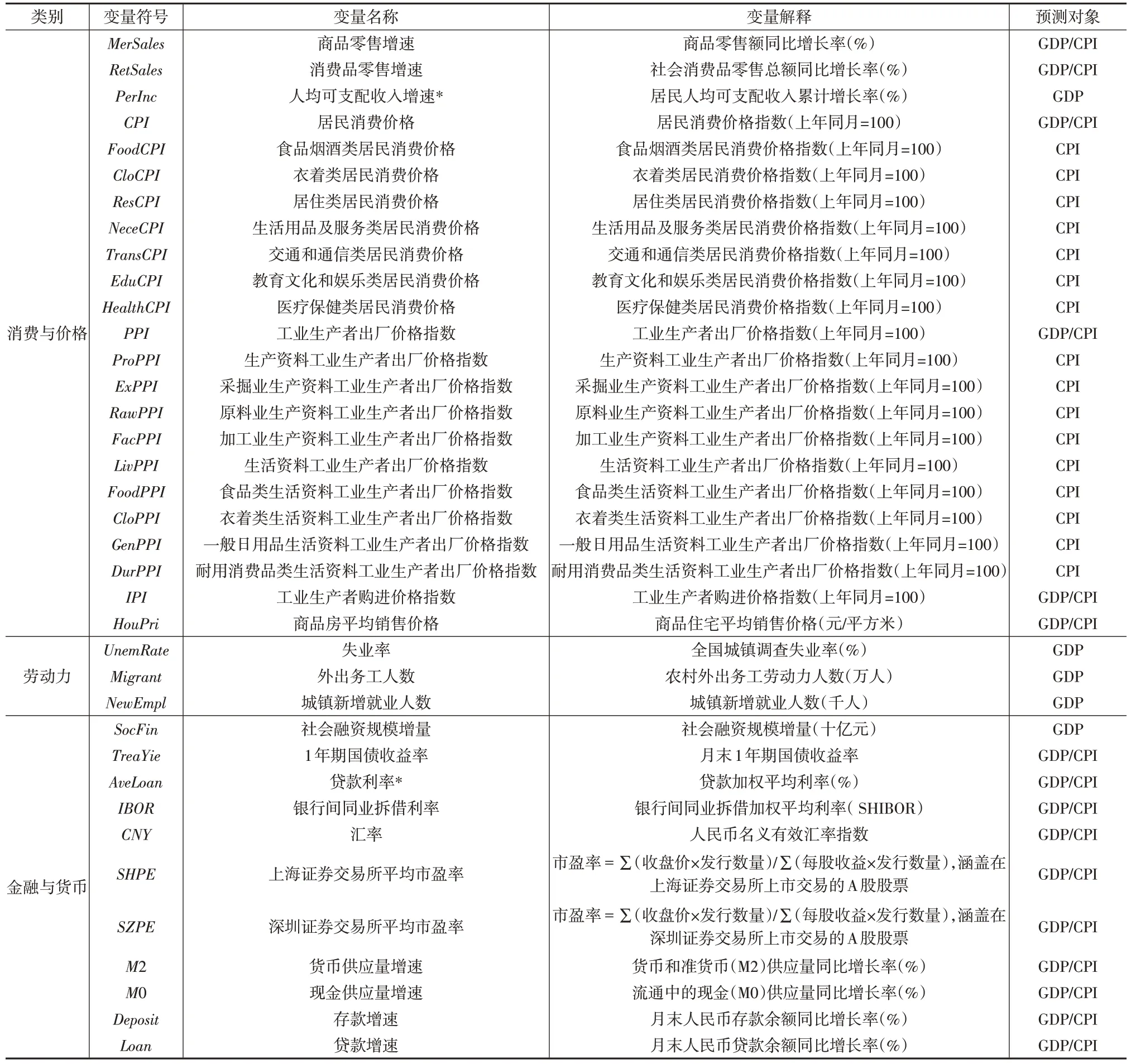
表1 数据集变量选择情况表（2）

2.2 数据处理

数据处理主要包括缺失值填补、标准化处理、季节性调整等，在将季度指标数据视为同时期对应月度数据最后一期的数据时，其余时期的数据将视为缺失值，获取的宏观数据中还有一些月份也存在缺失值，如“春节效应”导致部分指标缺少1月份的数据等。缺失值填补、标准化处理都纳入动态因子模型初始环节中，标准化处理则在主成分的因子提取中。缺失值填补是基于卡尔曼滤波进行的，引入实时估计得到的动态因子对缺失值进行动态补充，将缺失值视为上一期观测值与权重的乘积，再加上动态因子的和，然后根据卡尔曼滤波估计结果进行更新。本文还对除比率、增长率之外的指数数据采用X-12-ARIMA 等进行季节性调整。

3 实证研究

3.1 宏观经济实时预测与评价方法

按照上述步骤，利用本文所提及的两阶段、三阶段平滑方法，分别以我国实际GDP 同比增速、CPI 同比增速为被预测变量，纳入动态因子模型中进行实时预测，每月预测一次，将得到的拟合值与实际值，以及与单指标预测方法ARMA、ARMA-GARCH 的结果进行比对。参照以往做法，采用均方根预测误差（RMSFE）、平均绝对百分比误差（MAPE）、对称平均绝对百分比误差（SMAPE）评价采用两阶段与三阶段固定区间平滑算法的实时预测效果。

3.2 GDP实时预测效果分析

下页图1为GDP同比增速的预测值与实际值比较，每月实际值是将该季度GDP按月填充。2020年以前经济处于平稳发展阶段，宏观经济各部门、各要素保持惯性运行状态，因此，2018—2019年两阶段与三阶段固定区间平滑算法的预测值、实际值的偏差较小，且两个预测值的差别也不大，而ARMA、ARMA-GARCH 虽然保持了GDP 增长趋势，但预测值与实际值仍有较大偏差。2020 年以后重大公共卫生事件对经济的结构性冲击导致GDP增长呈现“V”型反转与不稳定波动，非常规情况下两阶段与三阶段算法实时预测均出现偏差，体现了预测的时滞性，如2020年第一季度的“V”型反转、2021年第一季度的“倒V”型反转，当期均无法直接捕捉到，相比较而言，三阶段算法响应速度较快，体现了对经济增长“V”型反转的更快预测，因为对先验信息利用更充分以及前次的前向滤波平滑，对月度频率数据提取因子的再次平滑可以较好地预测季度数据值，所以使得3月、6月、9月、12月的预测值更接近实际值，两阶段算法则具有1 期的滞后性。ARMA、ARMA-GARCH 则会出现5 期以上的滞后性，只是趋势上的预测，难以提取更多信息，因此效果较差。

图1 不同方法GDP同比增速预测值与实际值比较

下页表3 显示了采用RMSFE、MAPE、SMAPE 三个指标评价不同方法的预测效果的结果。可以看到，非常规状态下各方法的预测误差均变大，但相比较而言，三阶段算法预测误差最低，因此，其预测精度最高，两阶段算法次之，ARMA、ARMA-GARCH的预测精度远低于前两者。

表3 GDP同比增速预测的效果评价

3.3 CPI实时预测效果分析

下页图2和表4为CPI同比增速的实时预测结果与效果评价结果。可以看到，经济平稳运行状态时CPI增速在较窄区间内波动，两阶段、三阶段算法能够较好地预测其走势，非常规状态下CPI增速波动区间变大，“V”型反转出现较为频繁，导致部分时点两阶段、三阶段算法预测具有滞后性，如2020年5月、2021年5月、2022年1月，由于CPI是月度发布指标，三阶段算法也无法做到对反转信号的快速响应，因此需要更高频的周度、日度数据来实现有效实时预测。另外，在预测精度上，三阶段算法也是最高的，ARMA、ARMA-GARCH的预测精度都相对较低。

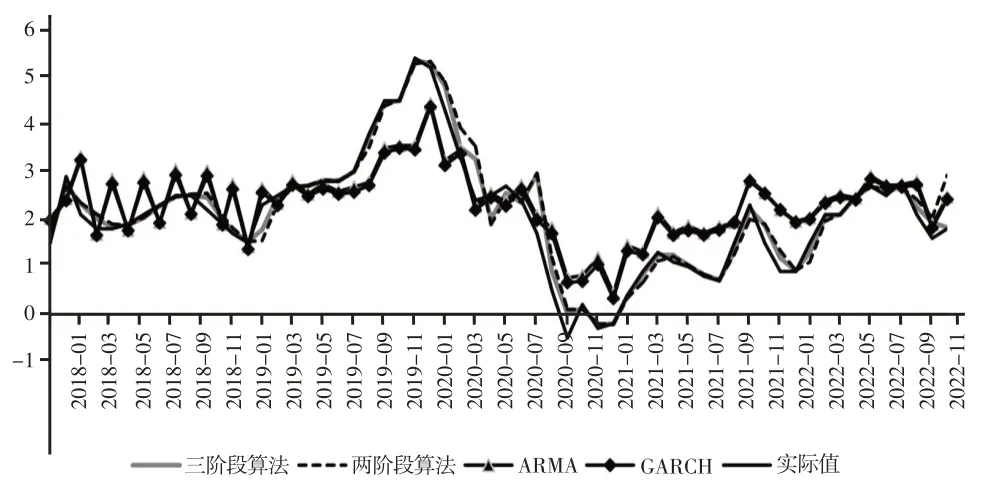
图2 不同方法CPI预测值与实际值比较

表4 CPI同比增速预测的效果评价

4 结论

本文将基于卡尔曼滤波算法改进的三阶段固定区间平滑算法引入高维混频数据的动态因子模型参数估计过程，令其替代传统的两阶段平滑算法，并应用于我国宏观经济预测中以探讨该种估计方法的优势与不足。实证结果表明：（1）实时预测能够较好地预测经济平稳状态下的发展趋势，预测偏差较小，但是当经济处于非常规情况下，针对“V”型反转的预测会出现时滞性；（2）基于卡尔曼滤波的三阶段固定区间平滑算法能够实现对现有数据的再次平滑，相比两阶段平滑算法，有效利用了现有数据中的公共因子与特异因子的先验信息，并通过再次前向滤波平滑，预测精度进一步提升，针对“V”型反转走势也能快速响应，应用月度指标能够较好预测当季GDP增速，但面对月度CPI 增速预测时实时响应能力不足，因此，需要结合更高频的周度、日度数据等，应用三阶段固定区间平滑算法才能实现对宏观经济的多层面、高质量的监测与预警。