基于元胞自动机的实时降雨下流域洪水淹没过程分析

蔡木良，支欢乐，李文欢，黄 河，刘 贤，蒋水华，张秀平

（1. 国网江西省电力有限公司电力科学研究院，江西 南昌 310058； 2. 南昌大学工程建设学院，江西 南昌 330031；3. 中铁水利水电规划设计集团有限公司，江西 南昌 330029； 4. 江西省水利科学院，江西 南昌 330029）

0 引 言

近年来，结合数字高程模型（DEM）、水动力模型和地理信息系统（GIS）推求洪水淹没范围是水利应用领域的研究热点之一。强暴雨引起的具有威胁性的洪水是我国最为严重的自然灾害之一，往往会对流域出口及下游缓坡及山间盆地人口密集地带造成重大的人员伤亡和财产损失。目前我国尚未建立完善的基于降雨资料的洪水灾害预评估体系。如何快速预警预报暴雨洪水灾害是当前迫切需要解决的难题。

建立一个适用性及可推广性强，并且具有实际物理意义的洪水淹没分析模型是实现暴雨洪水灾害预警预报的重要前提。传统的预警预报方法根据临界雨量等预警指标和结合风险区域地形地貌等特征进行综合评断［1］，然而该方法确定预警指标临界值缺乏科学依据，无法获得准确的暴雨洪水灾害淹没信息，给决策者制定有效的洪灾防灾措施带来了困难。结合GIS和分布式水文模型是目前提倡的洪水灾害预警预报方法，可考虑降雨资料的可获得性以及预警预报技术的可推广性。其中采用相对简单并具有一定物理意义的水文模型［2］，是目前使用较为广泛的方法之一［3-7］。如刘仁义［3］提出了有源和无源淹没情形下基于种子蔓延的淹没区计算方法，但是该方法运算效率及计算精度会受到种子点位置及数据精度等因素影响。冯丽丽等［7］尽管基于GIS 技术运用无源淹没和有源淹没方法确定洪水淹没区范围，但是不能考虑实时降雨因素进行洪灾预警分析。综上，虽然基于GIS技术的无源淹没算法较为简便，但是大多难以准确模拟实时降雨造成的洪水淹没过程。另外常用的洪水淹没分析方法如水动力学模型，虽然能够模拟降雨和河道汇流过程得到相对准确的结果，但是需要的输入参数较多，运算过程复杂，对数据精度要求较高。这些方法容易受到数据观测与采集手段的限制，在无资料流域或无法确定河道上游断面流量的情况下具有一定局限性。此外，上述方法建模过程繁琐，且模型所需文件数据较多，数值求解微分方程的近似解时存在很大困难，导致实际工程应用非常有限［8-10］。

相较之下，元胞自动机为模拟洪水淹没过程提供了一种有效的分析手段［8-12］。如王复生［8］运用元胞自动机模型模拟流域降雨径流、产汇流和洪水淹没的时空变化过程。Dai 等［12］考虑水文因素影响，构建了三层空间连接城市屋顶、地面和人工排水网络，建立了基于元胞自动机的水文和NPS 污染模型。孙海等［13］提出了基于栅格水动力学的元胞自动机模型，获得了与MIKE 21 模型相近的计算结果，并有效提高了计算效率。王威等［14］建立了基于“体积法”与元胞自动机的溃坝洪水演进模型，能较好地模拟城市地区溃坝洪水演进的时空特性。刘伊萌等［15］利用CADDIES-2D 洪水模型模拟了北京五环内城区内涝情况，研究发现CADDIES-2D 模型的模拟精度优于Flood Area模型，但稍逊于BUW 模型。综上，相比于无源淹没分析方法，基于元胞自动机的洪水淹没分析模型可以充分考虑流域下垫面条件。相比于水动力学模型，该模型在保证计算精度的前提下需要的模型输入参数更少，同时元胞自动机受数据的影响更小，不仅可以计算获得流域内降雨产汇流量，而且可以动态输出径流空间变化过程，因而具有较大的应用前景［16］。

以江西省宜春市袁州流域作为研究区域，首先基于GIS 技术生成数字高程模型格网数据，结合流域下垫面条件，求解洪水淹没范围及水深，进而建立基于元胞自动机的洪水淹没分析模型。将实时预报的未来24 h 降水资料作为模型输入，发生最大暴雨洪水灾害的区域作为模型输出。同时，基于无源淹没分析方法和MIKE SHE 的坡面流模型计算结果验证所建模型的有效性。

1 洪水淹没过程分析方法

在引入基于元胞自动机的洪水淹没分析模型之前，首先简要介绍洪水淹没过程分析的无源淹没洪水分析方法。

1.1 无源淹没洪水分析方法

无源淹没分析方法基本原理是运用GIS 技术遍历DEM 上每个点的高程值，一旦该点的高程值小于给定洪水水位，即将其加入至淹没区域。该方法仅将区域总降水量作为输入，适用于大面积区域降水情况下洪水淹没分析，计算相对简单。无源淹没分析方法将复杂的洪泛区域地形划分为若干个相等的面积单元，以点（x，y）代表单元所在的地理位置，各单元淹没水位和地面高程各不相同，可得单元网格对应的淹没水深D（x，y）为：

式中：H（x，y）为单元网格对应的淹没水位；E（x，y）为单元网格对应的地面高程值。

考虑到区域下垫面的不均匀性，通过分析地表降雨经过蒸散发、植被截留、土壤下渗等一系列损耗后产生的径流量过程，可以得到单元网格处由降雨产生的径流深R（x，y）为：

式中：α（x，y）为单元网格处的径流系数；P（x，y）为单元网格处的降雨深度。

同时，根据无源淹没基本理论，由下式可确保洪水来水量与洪水淹没范围内总水量相等：

式中：i=1，2，…，n；Ri（x，y）和Di（x，y）分别为第i单元网格处径流水深和淹没水深；Δσ为单元网格面积。

1.2 基于元胞自动机的洪水淹没分析模型

元胞自动机（Cellular Automata）是将系统划分为规则的元胞网格，每个网格处于有限状态并受相邻元胞状态的影响［8］。在每个模拟步中，所有元胞状态都根据指定的转换规则进行同步更新。本文建立的基于元胞自动机的洪水淹没分析模型，将流域产汇流和洪水淹没时空分布过程分为3 个阶段：①雨水降落到地表时经植被拦截、土壤非饱和带吸收作用后，产生净雨；②净雨经流域坡面、饱和带、非饱和带作用，汇聚形成径流；③最终形成洪水［17，18］。该模型主要由元胞空间、元胞邻域、元胞状态和转换规则这四部分构成，按照既定规则进行动态模拟，主要特点如下：

（1）采用最常见的二维正方形元胞，以确保元胞空间划分与研究区域地形的DEM格网划分一致，便于数据提取、转换、计算和数据前处理以及结果可视化输出。

（2）元胞邻域是指中心元胞周边的其他元胞，与中心元胞有着直接的演化关系。本文研究中邻域类型选择摩尔型（Moore），定义每个元胞的左上、上、右上、左、右、左下、下和右下这8 个相邻元胞为其邻域元胞（见图1），其中蓝色元胞为中心元胞，相邻的红色元胞为邻域元胞。洪水在360°方向上的演进过程皆为连续，且只与相邻的水量单位有关。

图1 摩尔型邻域关系Fig.1 Moorish neighborhood relationship

（3）元胞状态是洪水演进过程中的状态量和参数，需要储存在元胞空间内进行相应的计算［9］。根据其各自属性和特征，可分为静态量集和动态量集。表1给出了需要采用的元胞状态量参数。

表1 元胞的状态量参数Tab.1 Parameters for state variable set of a cell

（4）制定元胞转换规则是构建元胞自动机模型的核心环节。元胞自动机模型中的元胞转换规则主要有产流规则和汇流规则。这些规则主要用于计算水流的流动方向和进行水量分配。水流方向与中心元胞与其邻域元胞之间的水位差有关，如果某中心元胞的水位最低，则不进行水量分配。先计算中心元胞及8个领域元胞的水位平均值：

式中：H0为中心元胞水位；Hi为未被去除的邻域元胞的水位；m为未被去除的邻域元胞的数目。将水位大于平均值（Hi＞ave）的邻域元胞去除，计算剩余邻域元胞与中心元胞的水位平均值，并继续剔除水位大于平均值的邻域元胞，重复上述步骤直到没有邻域元胞被剔除，即剩余的邻域元胞水位都低于平均值。接着，再选择剩余的邻域元胞作为该中心元胞水量分配的对象，使中心元胞与剩余邻域元胞具有相同的水位。按照最小差异算法，中心元胞向剩余邻域元胞进行水量分配，直至达到平均水位。元胞水流流速采用以下曼宁公式推求：

式中：V为流速；h为中心元胞水深；s为坡度；n为糙率。

据此，可进一步得洪水由中心元胞流向邻域元胞的流动时间为：

式中：L为中心元胞与邻域元胞的距离。在汇流模拟过程中，时间步长t的大小决定了流量值。

邻域元胞的实际流量q为：

在进行水量分配时，需要注意以下两点：①当计算所得的分配水量大于该元胞水深时，分配水量需要按照该元胞的水深进行计算；②当中心元胞与邻域元胞水位相同时，则不再进行水量分配。为保证模型运行效率和稳定性，通常将时间步长t设置为小于大部分洪水流动时间的值，以防止水流在某一个时间步内穿过元胞。每个元胞将水量分配给其邻域元胞的同时，也会获取来自其他邻域元胞的洪水，因此每个时间步长的元胞洪水量Qi计算公式为：

式中：qi表示中心元胞在该时间步长内的洪水流入量，来自其周边8 个邻域元胞；qt表示中心元胞在该时间步长内的洪水流出量；Qi-1表示通过上个时间步计算的元胞洪水量。

2 案例分析

下面依托江西省宜春市袁州流域，采用所建的基于元胞自动机的洪水淹没分析模型模拟洪水淹没过程。江西省宜春市袁州地处江西省西部，东邻钢城新余，南接古城吉安，西毗煤都萍乡，西北连湖南腹地。DEM 提取的流域数字特征包括单元格网的流向、汇流路径、河网间的拓扑结构等。江西省宜春市袁州流域DEM高程图如图2所示。

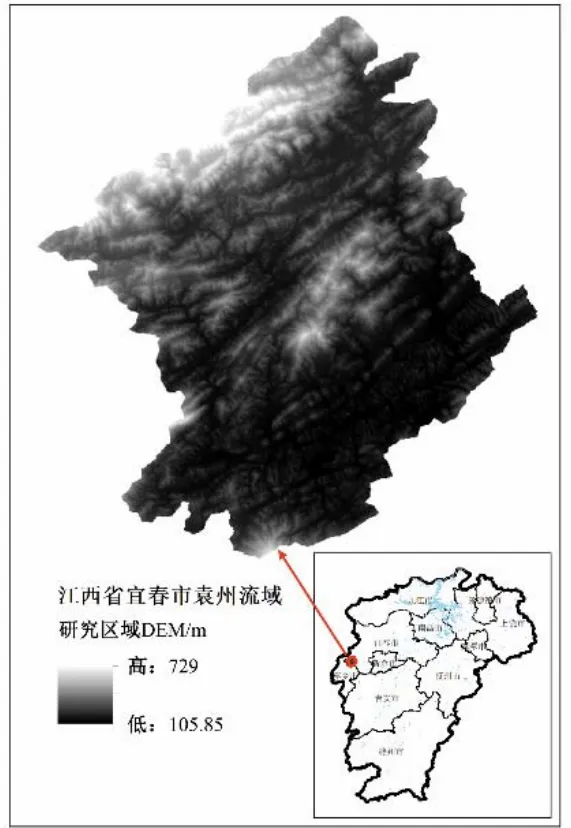
图2 江西省宜春市袁州流域图Fig.2 Diagram of Yuanzhou watershed in Yichun City，Jiangxi Province

图3 给出了以2021 年5 月28 日12 时至5 月29 日12 时的总降雨量生成的江西省预报降雨数据分布图。由图3 可知，该时段内袁州流域地区总降雨量高达78 mm，极有可能出现因短历时强降雨诱发的洪水灾害。研究流域采用30 m×30 m 格网，以2021年5月28日12时为计算初始时刻，采用30 m×30 m 分辨率的DEM高程格网数据和降雨格网数据，其中高程格网数据和降雨格网数据保持一致。

图3 江西省2021年5月28日降雨数据分布图Fig.3 Distribution of rainfall data in Jiangxi province on May 28， 2021

2.1 模型计算结果

采用所建的基于元胞自动机的洪水淹没分析模型计算降雨产流量时，考虑植被截留量和土壤下渗量这两种降雨损耗，采取径流系数表示降雨产生径流的损耗过程。根据江西省暴雨洪水查算手册［19］以及研究区域流域特征，取该研究区域的径流系数为0.57。进行汇流计算时，需要输入每个元胞DEM 的格网数据和产生的径流量数据。本文基于DEM 格网数据中3×3的元胞矩阵进行计算，首先筛选出径流流动方向及流量，求解单位计算步的中心元胞至领域元胞的流动水量，得到规定时间内洪水淹没范围及淹没深度。将降雨发生前即模型开始计算时刻的研究区域淹没面积视为0。为了更直观地呈现降雨径流过程中流域洪水淹没及变化过程，计算过程中记录各个时刻的元胞水位值，并以栅格数据的形式进行可视化输出，进而可得到4 个不同时刻（10 min、30 min、1 h 和2 h）的宜春市袁州流域洪水淹没数据，如图4 所示。表2 给出了不同时刻对应的淹没面积。另外，根据黄中发［20］和表3 基于淹没水深的洪涝灾害等级划分，将研究区域可分为轻涝、中涝、重涝和特涝这4 个等级。

表2 宜春市袁州流域淹没面积km2Tab.2 Inundation area of Yuan Zhou watershed in Yichun city

表3 洪涝灾害等级划分Tab.3 Classification of flood disaster levels

图4 不同时刻的流域洪水淹没水深结果Fig.4 Flood water inundation results for different durations using the established model

由表2 可知，这4 个时刻宜春市袁州流域的洪水总淹没面积分别为136.28、40.91、33.68、33.68 km2。10 min时最大淹没水深达4.93 m，淹没区域分布较为密集，主要是由于此时洪水主要汇集在山谷沟壑等区域。随着模拟时间的延长，轻涝淹没面积和总淹没面积逐渐降低，30 min 时最大淹没水深逐渐增加至8.90 m，这是因为山谷沟壑等区域的洪水逐渐汇集到河道区域。由图4（c）可知，1 h 时河道支流洪水逐渐减少，洪水贯通区逐渐增大，最大淹没水深逐渐增加至10.18 m。此外，由图4（c）和（d）可知，模拟时间超1 h 后，流域内淹没范围基本不变，最大淹没水深逐渐增加至10.62 m 后逐渐减小。此外，洪水并非全部聚集在地势低的区域，而是有条件地选择行进路径，即流入地形高程比其周围淹没水位更低的区域，符合水流运动的基本规律。综上可知，所建模型能够有效模拟洪水淹没过程及时空分布特性。

2.2 模型验证

本节分别采用无源淹没方法和基于MIKE SHE 的坡面流模型计算结果验证所建模型的有效性。首先，采用无源淹没分析方法基于宜春市袁州流域的30 m×30 m 高程点的格网数据E（x，y）以及降雨格网数据P（x，y），通过式（2）计算单个格网的径流深R（x，y），其中径流系数取值同样取0.57。进而根据洪水来水量与洪水淹没范围内总水量相等这一原则，联立式（1）和式（3）推求研究区域淹没水位。获得宜春市袁州流域淹没水位值之后，构建无源淹没洪水区域输出模型。接着依次对格网单元进行扫描，将格网单元的高程和给定洪水位进行比较，并把其中的淹没单元进行连接，计算淹没水深。最后获得最终的洪水总淹没面积为6.73 km2，最大淹没水深为13.35 m（见图5）。然而，利用无源淹没洪水分析方法得出宜春市袁州流域淹没灾害等级最高区域主要集中在流域西南部地势较低处，显然与实际洪水灾害特征不符。这是由于无源淹没分析方法的基本原理是通过遍历所有栅格单元，从中找出淹没栅格，虽然实现过程较为简单，但是不能考虑地域连通性，导致高程值低于淹没水位H的栅格都被计入淹没区域。

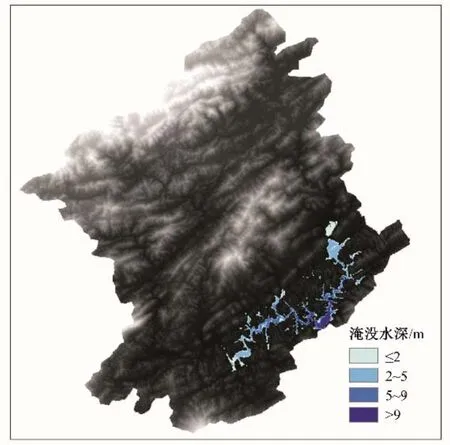
图5 无源淹没分析方法的淹没水深结果Fig.5 Inundation water depth results using the non-source inundation analysis method

接着，采用MIKE SHE 的坡面流模型进行洪水淹没过程分析。坡面流模块主要采用扩散波对圣维南方程组进行近似分析，径流系数同样取值为0.57，糙率初始取0.025。MIKE SHE的坡面流模型运行时间与元胞自动机洪水淹没模型相同。图6给出了模拟得到的坡面流淹没水深分布。由图6可知，MIKE SHE的坡面流模型获得的总淹没面积达34.56 km2，与图4（d）中历时2 h 的总淹没面积仅相差0.88 km2，较为吻合。图6 和图4（d）的淹没水深分布基本一致表明，所建模型能够准确模拟洪水淹没过程。表4 进一步比较了3 种不同方法洪水淹没结果。由表4可知，相较于无源淹没分析方法，所建模型计算精度更高；相比于MIKE SHE 的坡面流模型，所建模型在满足计算精度的同时，无需进行复杂的模型计算，更便于实际工程推广应用。

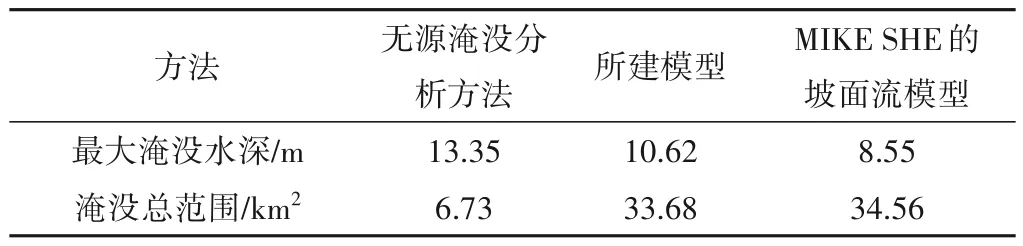
表4 不同方法洪水淹没结果的对比Tab.4 Comparison of flood inundation results obtained from different methods

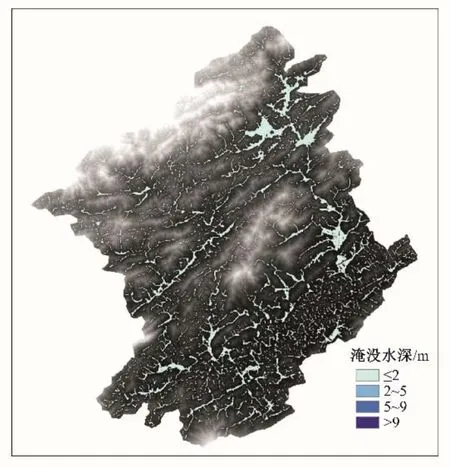
图6 MIKE SHE坡面流模型的淹没水深计算结果Fig.6 Inundation water depth results using MIKE SHE overland flow model

2.3 参数敏感性分析

为探讨输入参数的影响，本节采用所建的元胞自动机洪水淹没分析模型对糙率n进行敏感性分析，调查不同糙率n对研究区域不同时刻（30 min、1 h 和2 h）最大淹没水深的影响。糙率n分别取0.01、0.025 和0.04，即是在基准值0.025 的基础上分别增加和减少0.015，其他参数保持不变［20］。计算参数敏感性指标和H0.04分别表示糙率n取0.01、0.025和0.04的最大淹没水深。参数敏感性指标α值越大，表示该参数对研究区域最大淹没水深的影响越大。表5给出了糙率n的敏感性分析结果。由表5 可知，随着模拟时间的延长，糙率n对研究区域最大淹没水深的影响逐渐减小。因此，对于短时间洪水淹没过程，糙率n的敏感性较大，而随着模拟时间的延长，糙率n的敏感性逐渐减小。

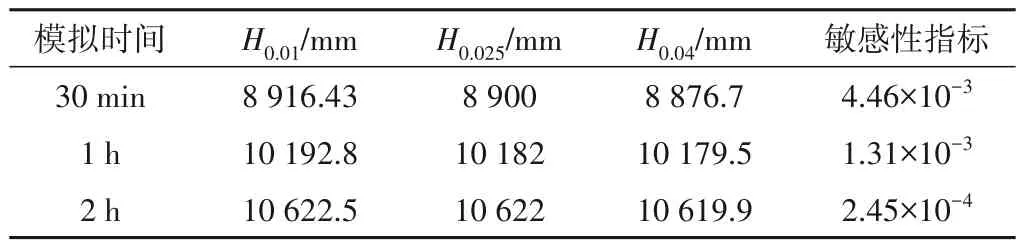
表5 糙率n的敏感性分析结果Tab.5 Sensitivity analysis results of roughness n

3 结 论

依托江西省宜春市袁州流域，建立了基于元胞自动机洪水淹没分析模型，进而基于实时降雨数据获得了研究区域不同时刻的淹没水深和淹没范围，并通过无源淹没分析方法和MIKE SHE 的坡面流模型计算结果验证了所建模型的有效性。主要结论如下：

（1）无源淹没分析方法虽然计算简单，但是不仅只能考虑总降雨量对研究区域的淹没结果的影响，而且忽略了研究区域下垫面及地形连通性的影响，无法考虑降雨产汇流过程，获得的洪水淹没计算结果与实际情况不符，不利于洪灾预警措施方案的制定。

（2）建立的基于元胞自动机的洪水淹没分析模型可以充分考虑研究区域下垫面条件以及降雨的产汇流过程的影响，更加合理地模拟洪水淹没过程，动态显示不同时刻的洪水淹没过程。相较于无源淹没分析方法，所建模型具有更高的计算精度；相比于MIKE SHE 的坡面流模型，所建模型在满足计算精度的同时，无需进行复杂的模型计算，更便于实际工程推广应用，从而可为强降雨下洪水灾害风险评估以及防汛抢险决策方案的制定提供了参考。

（3）所建模型的元胞大小和计算效率成反比，为保证计算效率，本文模型采用的元胞边长较大（为18 m），在一定程度上会影响对真实地形条件的模拟精度。此外，本文模型只考虑了中心元胞向邻域一个元胞进行分配水量。为更真实反映工程实际情况，关于中心元胞向邻域多个元胞的水量分配问题还有待进一步研究。