电导率调制体声波谐振器FDTD仿真研究

赵小龙,李安鸽,贺永宁

(1.西安交通大学 电子与信息学部微电子学院, 西安市微纳电子与系统集成重点实验室, 陕西 西安 710049;2. 西安微电子技术研究所, 陕西 西安 710075)

0 引言

体声波谐振器可用于制作射频滤波器、声放大器和探测器等[1-4]。基于压电半导体材料ZnO、AlN和GaN等的体声波器件,利用其半导体特性可以实现特性可调的滤波器及光电探测器等。赵小龙等[5-6]基于ZnO单晶实现了体声波谐振X线探测器,研究表明,该器件的响应特性与ZnO电导率在X线照射下的变化有关,故需对电导率的调制效果进行深入研究。于小利等[7]基于FDTD法对体声波谐振器的特性进行了数值仿真研究,但关于电导率的影响规律未有仿真方法报道。因此,本文基于一维模型,利用FDTD仿真法实现了体声波谐振器谐振频率的电导率调制规律研究,为基于ZnO体声波器件的可调滤波器、声放大器和探测器等的优化设计研究提供了理论支撑。

1 仿真方法

本文以一维模型为例,介绍了电导率对体声波谐振器特性影响的数值仿真法。这里忽略电极的影响,只考虑体声波在压电半导体中的传播。根据压电材料的体声波理论[8],波动方程:

(1)

式中:ρ为密度;u为质点位移;t为时间;ζ为应力;x为位置坐标。

本构方程:

ζ=cS-eE

(2)

D=εE+eS

(3)

式中:c为弹性柔顺系数;S为应变;e为压电系数;E为电场强度;D为电位移矢量;ε为介电常数。

应变与质点位移的关系为

(4)

电场与电势的关系:

(5)

式中φ为电势。

高斯定理:

(6)

式中Q为电荷密度。

考虑漂移电流的连续性方程:

(7)

式中:Jc为传导电流;σ为电导率。

为了减少求解的未知量的个数,对上述方程式消去S、ζ和E,可得:

(8)

(9)

(10)

(11)

由式(8)-(11)可求解4个未知数。根据方程形式对各个物理量在空间上进行离散,离散方法如图1所示。

图1 ZnO体声波谐振器离散方法示意图

根据图1离散方法,则式(8)的差分形式为

(12)

式中n和k分别为时间和空间离散角标。

为了提高仿真精度,式(9)采用四阶Adams-Bashforth差分方法[9]为

(13)

式(10)、(11)的差分形式分别为

(14)

(15)

边界处的应力为0,另外在边界处施加外加偏压Vs,故边界条件可表示为

ζ(x=0)=ζ(x=L)=0

(16)

φ(x=L)-φ(x=0)=Vs

(17)

由于电势是相对的,故在计算中可取:

(18)

初始时刻,各个场分量都为0。由式(12)、(13)可知,当前时刻的u和Q值可由前一时刻的值获得,其他未知量通过式(14)-(17)联立方程组求得,数值仿真流程图如图2所示。

图2 数值仿真流程图

通过计算得到电位移矢量D后可得位移电流:

(19)

体声波谐振器的阻抗为

(20)

式中A为电极面积。

为了获得器件的阻抗谱,这里采用宽频信号Vs作为激励,此时器件的响应电流包含多个频率成分,则器件的阻抗谱可表示为

(21)

式中FFT(x)为傅里叶变化。

本文仿真参数采用ZnO体声波X线探测器的结构参数,ZnO层厚度为0.2 mm,器件面积为4 mm×4 mm[5]。

2 仿真结果与讨论

2.1 阻抗特性

仿真采用的电压激励波形为余弦函数调制的高斯脉冲。电压激励波形和电流仿真结果如图3所示。由图可见,当电压脉冲结束后,电流输出波形还在持续震荡,其频率约为13 MHz,此频率与该器件的谐振频率一致。

图3 仿真电压激励波形和电流计算结果

根据式(21)对电压激励波形和电流仿真结果进行处理,可得该ZnO体声波谐振器的阻抗谱。图4是电导率为0时仿真结果与理论式[8]的对比。由图可见,仿真与理论结果一致,表明本文仿真方法合理。

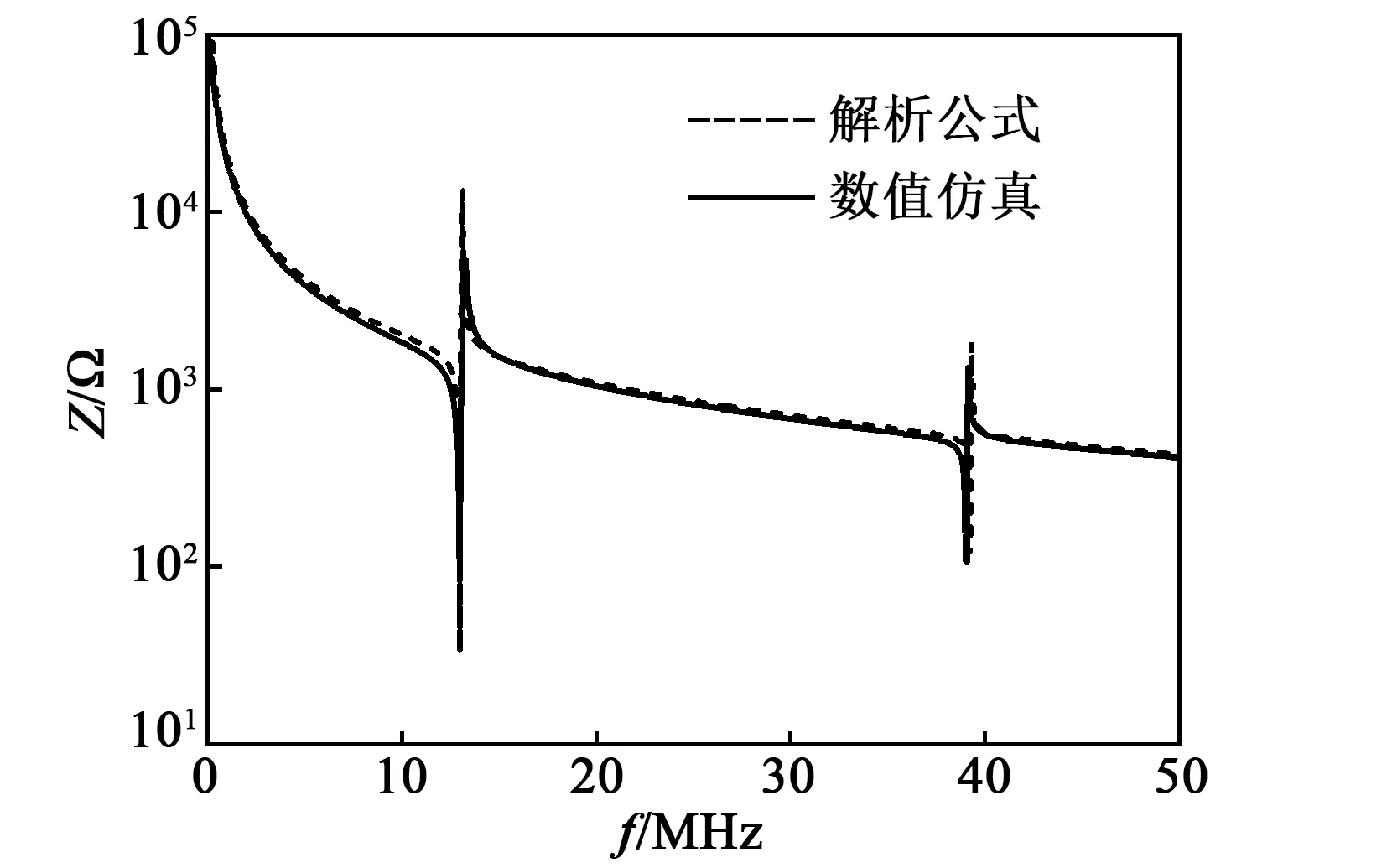
图4 ZnO体声波谐振器阻抗特性仿真结果

2.2 电导率的影响

通过改变ZnO的电导率可以研究电导率对体声波器件的影响。图5为改变电导率的阻抗特性仿真结果。由图可见,随着电导率的增加,谐振频率略为降低。该结论与文献[5]的理论模型一致,并可用于解释由于光电导效应导致ZnO体声波谐振器在X线照射下谐振频率下降的实验现象。

图5 改变电导率的阻抗特性仿真结果

图6为串联谐振频率随着电导率变化的仿真结果。由图可见,电导率较小,对谐振频率基本无影响;当电导率为1～30 mS/m时,谐振频率快速下降;电导率进一步增加时,谐振频率趋于稳定。由此可见,体声波谐振器的谐振频率随压电材料电导率的变化趋势与声表面波谐振器谐振频率随表面电导率的变化趋势一致。利用图6的仿真结果可以为体声波谐振光电探测器的设计提供指导。如为了提高探测器的灵敏度,需要选择电导率合适的ZnO材料,即电导率应选择图6中斜率最大的点,即约6 mS/m;如果需要尽量增大探测器的动态范围,则ZnO电导率可选择在1 mS/m附近。

图6 串联谐振频率随电导率变化仿真结果

文献[5]测试了ZnO单晶体声波谐振器的谐振频率随温度的变化关系,并且测试了ZnO单晶电导率随温度的变化关系。利用这些数据可给出ZnO单晶体声波谐振器的谐振频率随电导率的变化关系,如图7所示。图7同时给出了基于文献[5]的解析理论模型的计算结果。对照图6可见,FDTD仿真结果的趋势与实验值和解析模型一致,均表现出电导率为1～30 mS/m,对谐振器谐振频率的调制效果最显著。

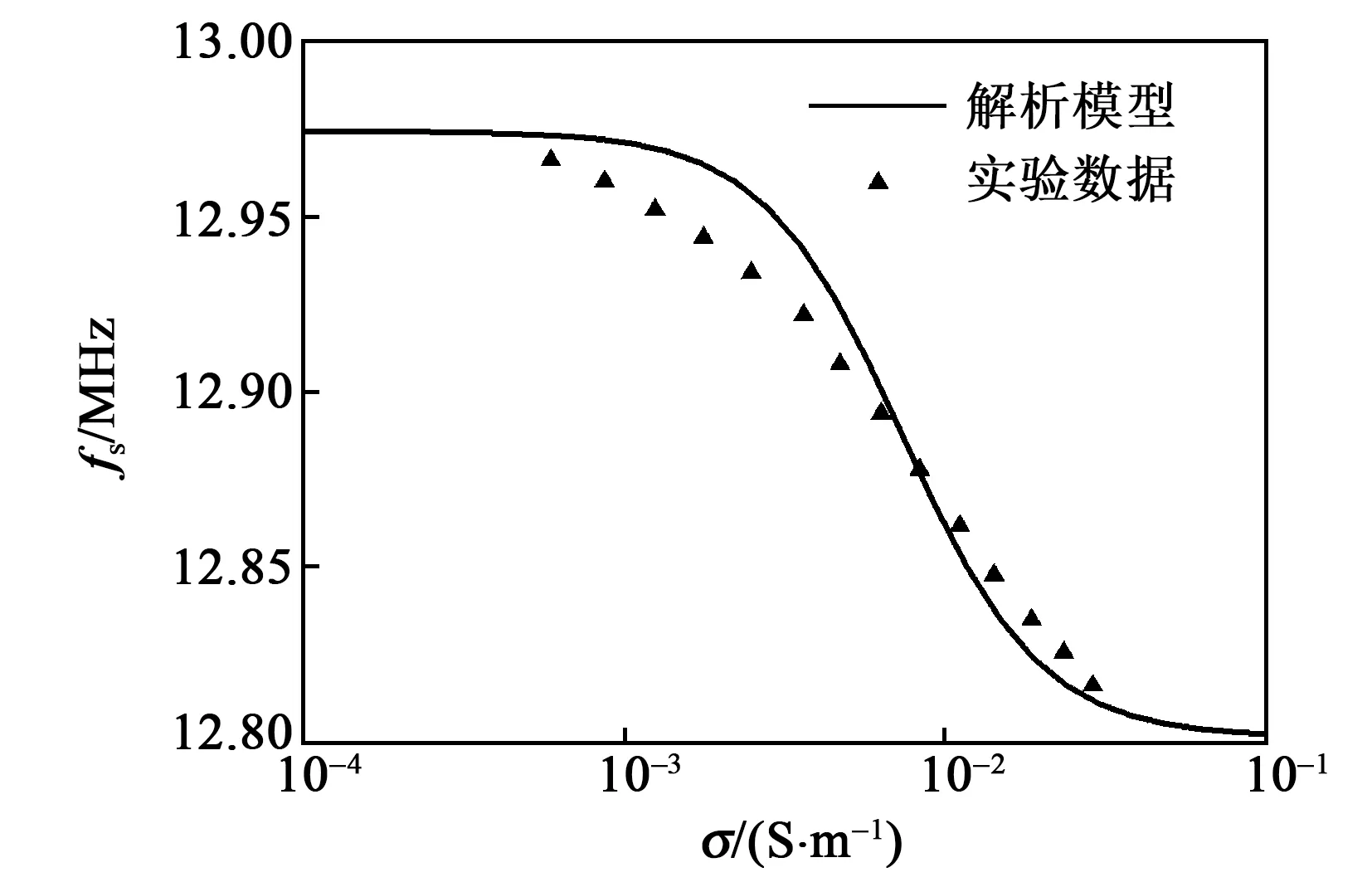
图7 ZnO单晶体声波器件串联谐振频率随电导率变化的实验值和解析计算曲线

图6中数值计算结果给出的谐振频率变化范围小于图7中的解析模型结果。由图3的仿真结果可看出,脉冲电压激励产生的位移电流为持续时间很长的振荡信号,由于仿真时间有限,该振荡信号被截断。这种截断的振荡信号在经过FFT变换提取谐振频率时将产生误差。利用Prony算法[10]替代FFT变换有望改善此问题,后续将进行进一步研究。

3 结束语

电导率调制体声波谐振器可用于声放大器、可调滤波器和探测器。本文采用FDTD数值仿真方法,研究了电导率对体声波谐振器谐振频率的影响规律。考虑漂移电流的连续性方程,采用四阶Adams-Bashforth差分形式以提高仿真精度。电压激励波形为余弦函数调制的高斯脉冲,通过仿真获得谐振器的电流输出时域波形,最后利用快速傅里叶变换获得器件的阻抗谱,从而可提取器件的谐振频率。仿真结果表明,随着电导率的增加,ZnO体声波谐振器的谐振频率逐渐降低,电导率为1～30 mS/m时,对谐振器谐振频率的调制效果最明显。