路径积分差分吸收激光雷达反演模型设计与测试

张豪伟，韩 舸，马 昕，龚 威，王 琦

（1.武汉大学 电子信息学院，湖北 武汉 430079；2.武汉大学 遥感信息工程学院，湖北 武汉 430079；3.武汉大学测绘遥感信息工程国家重点实验室，湖北 武汉 430079；4.国家国防科技工业局 重大专项工程中心，北京 100101）

0 引言

政府间气候变化专门委员会（Intergovernmental Panel on Climate Change，IPCC）第五次报告确认人为碳排放是全球变暖的主要因素。近年来，世界多个主要碳排放国家相继确立了碳中和目标，标志着人类社会再次在共同应对气候变化的议题上达成一致。准确、有效的碳监测是制定和审查减排措施的关键工具，也是国际间合作的互信基础。利用大气二氧化碳（CO2）浓度观测数据推算CO2通量，正逐步成为标准方法，可以补充现有“自下而上”核算体系的不足［1-2］。目前全球CO2浓度监测方式包括地基观测和被动卫星观测。其中，CO2观测地面站点可以提供长时间、高精度的观测资料，但其数量有限、分布不均，无法为高分辨的CO2通量监测提供充足的观测资料。在过去10 年中，被动碳遥感卫星的快速发展，使得人类初步具备了获取大范围CO2浓度观测资料的能力［3-5］。该卫星观测资料促进了区域通量反演、植被碳汇监测、人为强点源核查和城市排放核算等应用科学的快速发展。与此同时，被动遥感技术的内在不足也引起人们的关注。由于依赖太阳光进行观测，且反演是一个欠定的优化过程，其CO2浓度产品性能易受气溶胶和云层干扰。高纬度和夜间观测资料的缺乏也限制了相关科学问题的研究［3-8］。

从2005 年起，美国、欧洲和日本等发达国家就开始了天基激光碳监测激光雷达的研制工作，期望利用主动观测机制的优势与被动遥感形成互补。ABSHIRE 等［9］在2011 年进行了1.572 μm 差分吸收激光雷达ASCENDS 科学飞行实验，基于10 s 的CO2浓度平均值，在相对恒定的二氧化碳柱浓度（XCO2）区域获得了2×10-6～3×10-6的误差；REFAAT 等［10］在2014 年进行了2.0 μm 差分吸收激光雷达实验，并基于获得的海洋和陆地剖面进行建模，其结果降低了CO2脉冲的距离偏差。除此之外，SINGH 等［11］在2017 年进行模拟实验，根据10 s的数据平均，项目的预期性能低于0.35×10-6。我国在该领域的起步较晚，但进展很快。朱亚丹等［12］在中国进行了1.572 μm 差分吸收激光雷达实验，通过对整个探测系统硬件进行评估，验证了机载实验的有效性。相成志等基于我国1.572 μm 差分吸收飞行实验对XCO2反演进行了方案设计。结果表明，对于即将进行的陆地［13］卫星任务，XCO2的预测相对随机误差小于0.3%。2022 年4月，大气环境监测1 号星的成功发射，标志着我国成为世界上首个具有激光碳监测能力的国家。

天基遥感碳监测的技术基础是路径积分差分吸收激光雷达（Integral Path Differential Absorption Lidar，IPDA Lidar）［14-23］。其通过差分吸收过程，抵消气溶胶、地表反射等因素，精准的测量大气CO2分子的吸收能力。该项技术是通过建立光学反演模型来反演大气中的XCO2。本文利用2019 年在秦皇岛地区获得的机载激光雷达数据［24-25］，分析IPDA Lidar 反演XCO2需要解决的重要问题，并相应的提出改进方法。在IPDA Lidar 反演模型中积分权重函数上下界的精确确定，涉及气象参数、飞机惯性导航信息、信号分解获取测距距离这3 个部分的信息。在该3 个参数中，信号分解获取到的CO2柱体长度信息在整个反演过程中起着非常重要的作用。因此，从准确测量CO2柱长的角度来降低CO2柱浓度反演误差可行。除此之外，差分吸收光学厚度的获取涉及对原始信号的处理。从参杂噪声的回波信号中准确去除基线并估计出回波能量是测算差分吸收光学厚度的关键基础。相对于常规的采用原始信号的离散数据积分，本文通过自适应的光谱能量进行建模，通过采用模型函数去积分获取回波能量。提出一个基于光谱能量的模型，可以准确匹配非高斯信号波形。在实际数据采集中，特别是在山或云地表类型引起的多子波回波的信号，可以提高IPDA Lidar 系统的探测性能。

1 设计思路

为了获得高精度的XCO2，提出的算法框架主要集中在2 个方面。首先，结合式（1）来优化激光柱长的精度，从而从分母角度得到优化积分权重函数；结合式（1）优化波形能量积分，从分子的角度得到差分吸收光学厚度。算法框架流程如图1所示。

图1 算法流程Fig.1 Flow chart of the algorithm

1.1 模型函数构建

Lidar 的回波信号被认为是几个高斯信号的叠加，信号具有近似对称的特点。但该特性通常会受到地形的影响而导致信号变宽，很难用一个方程来定量描述加宽的信号，且增大了差分吸收光学厚度和积分权重函数的计算误差。针对1.572 μm IPDA激光雷达回波信号，因为常规的波形拟合不能用高斯模型准确描述，所以提出了一种基于频谱能量模型的波形建模的新理论（式（3）），可以减少因信号展宽引起的DAOD 和IWF 的计算误差。结合实验中1.572 μm IPDA 激光雷达回波信号的实际情况，在式（2）的傅里叶变换形式的基础上引入多个参数［26］，这样修改后的模型效果可以减少波形的展宽效应。此外，信号的特征参数是通过整个回波信号公式的定量表达得到。频谱能量公式和修改后的公式如下：

式中：a=1/4（1/τr-1/τf）；b=1/4（1/τr+1/τf），τr、τf分别为上升时间和下降时间。

式中：d为子波形参数中心，并且该参数也代表CO2柱体的长度；a、b、c和f需要从离散的信号数据中被拟合获取基于波形方程。

此外，为了获得多种土地利用类型回波信号的精确模型参数，采用了基于式（3）的列文伯格-马夸尔特（LM）算法作为核心。LM 算法可以在以往模型参数的基础上，结合相应的约束条件进行深度优化，得到符合精度要求的非线性拟合结果。

1.2 模型函数对IWF 和DAOD 的优化

对于积分权重函数的优化，主要是对IWF 中的上限和下限进行修改。实验结果表明，当CO2柱长度误差小于3 m 时，在空间使用IPDA 激光雷达系统测得的XCO2柱误差会小于1%。从精确测量CO2柱长的角度来看，通过结合上述模型的优化参数d，改进IWF 反演是可行的。

IPDA 激光雷达发射器以200 μs 的间隔连续平行发射1.57 μm 的在线和离线光束。因此，该发射器可以被看作是对同一目标的两个连续距离测量，从而产生了冗余的观测测距信息。此外，尽管以式（3）为核心的LM 算法，但距离测量的观测值相对于真实值仍有误差。由于λon和λoff的波段距离是分别测量得到，所以两个观测值产生的距离测量值矛盾。为了平衡该矛盾，引入不等精度的直接调整理论。关于测量调整，一般认为权重是观测结果可靠性的相对评价指标，其与中误差的平方成反比。最有可能值公式用于获得高精度范围值，权重和最可能值公式如下：

式中：为λon或λoff对应的中值误差；Pn为在λon或λoff对应的权重；L为上述数据处理后λon或λoff的测量值。

紧接着，结合积分权重函数式（6）获取优化后的参数IWF为

式中：IWF为积分权重函数计算的结果；PSFC和p=0为积分上、下限参数由优化后的参数d、气象参数和飞机惯性制导信息决定；为CO2积分权重函数。

对于差分吸收光学厚度的优化，主要根据提出的模型方程（式（3））来拟合信号波形，以获得对信号方程的准确描述。此外，将优化后的参数输入到DAOD 函数方程，然后对方程进行积分，以恢复信号的能量。因此，与传统的数值离散积分和基于高斯核公式的积分相比，上述优化方法可以更准确地获得波形能量。其DAOD 函数方程如下：

式中：DAOD为差分吸收光学厚度函数；P、E的能量是由优化后的公式参数组带入到对应的式（3）计算所得。

在传统的TSP问题中，解构建图为所有城市节点的连接网，边的权值为两城市节点间的距离。在本文中，首先需确定所有待编配车组与除晚高峰外的待编配车次的成本矩阵Cij，其中行代表车组号，列代表列车车次；车次按时间从早到晚依次排列，成本矩阵中的每一个值都作为一个节点vij(第i个车组担任第j个车次)。在进行计划编制时需按照车次时间顺序依次进行编配，故将所有节点按从左到右的方向依次连接，当前节点仅可与右侧相邻列的所有节点连接，如图1所示。

1.3 模型验证

对于算法框架的验证，主要是对模型参数d的验证。如果模型参数得到准确，那么XCO2的精度也会有很大提高。在模型的参数组中，模型参数d也反映了CO2气体的长度，而且参数d可以验证。因此，模型参数d的验证可以反映算法框架的准确性，也代表模型对XCO2反演的准确性。

模型验证根据不同的地表类型，分别分为海洋和陆地。首先，在海面上用秦皇岛的潮汐数据进行验证；其次，用ICESat-2 的数据在平原和山区进行验证。因此，需要重新评估经纬度的偏移，以获得激光雷达足迹的准确表面高程值。然后，根据图2中D点的偏移激光雷达足迹坐标，将ICESat-2 的数据匹配为地表高程。受机载姿态角的影响情况，其导致真实的激光雷达足迹偏离了机下点如图2 所示。其中，O点代表1.572 μm IPDA 激光雷达信号发射的位置；D点代表1.572 μm IPDA 激光雷达信号接触到地面时的反射位置；而A点是机下点路径（OA）上的一点，其高度与D点在同一平面上。C、A、B点在同一仰角平面上，A、O、C点形成的角度等于俯仰角。在图2（c）中，N 和E 分别代表坐标轴上的北方和东方。总之，机下点的位置（即GPS 值）并不代表激光雷达足迹的真实位置。

图2 激光雷达足迹的偏离机下点的地理模型Fig.2 Geographical model of the deviation points of the lidar footprint

假设飞机的姿态角不发生变化，1.572 μm IPDA 激光雷达观测到的机下点路径是OA。然而，由于滚动角和俯仰角的综合影响，实验中1.572 μm IPDA 激光雷达观测到的路径是OD。所以AD是实际脚印和机下点的偏差距离（大约330 m）。因此，重新评估LiDAR 脚印的真实位置很重要，因为全球定位系统（GPS）数据并不代表激光雷达脚印的真实位置。对于该偏差距离的修正，使用以下公式来获得经纬度的偏差：

式中：LOD为被探测到的柱长距离，基于上述理论是图2（a）中的OD；Pa为俯仰角；Ra为翻滚角度；VN为正北方向的速度；VE为正东方向的速度；LAD、LAC和LCD分别为图2（a）中的AD、AC和CD距离；α为飞机的实际飞行方向与东面的偏差角度，并且α也代表飞机在实际飞行方向与东方之间的偏差角度；Δαβ为α和β角度差值；ΔLat和ΔLon为D相对于点A的偏移量。

1.4 模型评价指标

为了量化提出方法的合理性，选择均方根误差（RMSE），该指标用于量化模型的偏差。指标的计算公式为

式中：N为样本总的数目；Pi为模型计算的值；Ri为真实观测到的值。

2 实验结果

2.1 基于提出的模型实验结果

为了获得高精度的XCO2，根据上述的算法框架对每组信号进行同样的处理。在该过程中，建立模型方程，然后通过组合每个回波成分来获得模型参数，以适应信号。单个信号中多个子组件的处理结果如图3 所示。

图3 模型处理结果Fig.3 Model processing results

2.2 模型验证结果

为了进一步验证算法框架，根据验证思路和具体实验条件，将验证分为海面和陆地。对于海面的验证思路，主要是将飞机提供的GPS 值与飞机平台到海面的垂直CO2柱长和WGS 84 坐标系中的海面高度之差进行比较。而实时海面高度主要由2 部分组成，分别为验潮站（秦皇岛站）的高程和实时潮汐数据，如图4 所示。验潮站数据涉及1985 年高程系统数据与WGS 84 高程系统数据的转换，转换值是由EGM 2008 重力模型计算得到。

图4 海面区域算法验证结果Fig.4 Verification results of the sea area algorithm

在图4 中，将GPS 高度的值与校正偏差后的值（该值为校正后的垂直CO2柱长与实时海面高度两个值之和）进行比较。结果显示，相对于约6 800 m 的测量高度，算法框架在海面上的精确度为0.94 m。此外，皮尔逊系数为1.00，表明数据之间在0.01 的水平上存在显著的相关性，同时进一步表明算法框架在海面上的准确性具有很高的鲁棒性。

为了验证模型对陆地的影响，比较了GPS 数据与偏差修正值之间的差异如图5 所示。

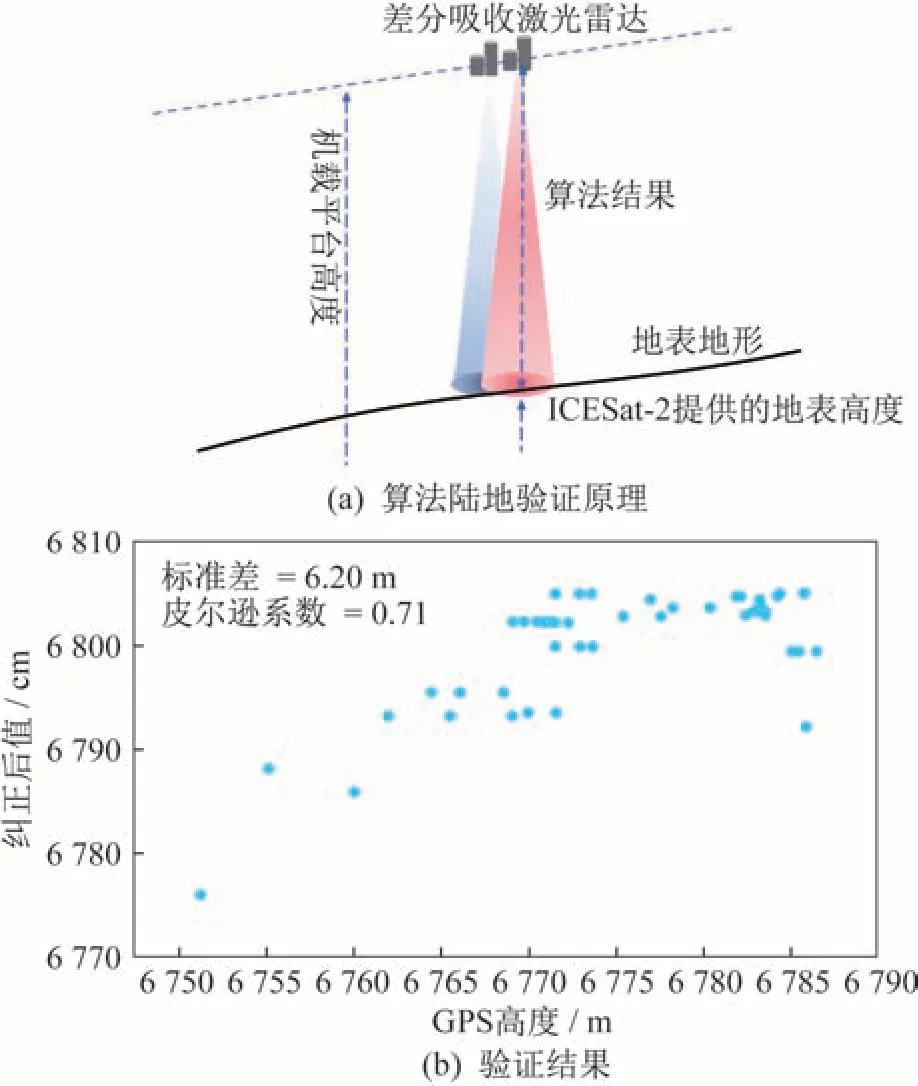
图5 陆地区域算法验证结果Fig.5 Verification results obtained by the land area algorithm

偏差修正值主要包括2 个项目，即垂直CO2柱距（即图5 中的算法结果）和相应激光雷达足迹的表面高程值。ICESat-2_ATL08 地形的高度误差平均值在平原地区小于0.05 m，在山区小于0.5 m［27］。考虑到IPDA 激光雷达数据和ICESat-2_ATL08 数据都是WGS 84 坐标系，使用ICESat-2_ATL08 数据作为表面高程输入数据。在图5 中，展示了算法模型在陆地上的验证结果，精度为6.20 m。该算法框架在陆地上的低精度主要是由于验证数据集的原因。为了增加高精度验证数据的数量，采集了从2018 年12 月到2021 年12 月的ICESat-2_ATL08 数据。而且使用了8 m 的矩形框范围，以匹配ICESat-2 和1.572 μm IPDA 激光雷达的足迹数据。但如果局部地形复杂时，会带来一些误差。此外，与2019年3 月采集的1.572 μm IPDA 激光雷达数据相比，验证数据存在一定的误差。因此，对于模型的验证，在海面上的验证更具有代表性。

2.3 二氧化碳反演结果和精度评估

不同积分时间下的XCO2反演结果如图6 所示。在图6（a）中XCO2反演在海洋上的波动明显大于陆地。图6（b）清晰地展示了XCO2在整个飞行轨迹上的变化趋势。海洋区XCO2最低，平原区XCO2最高。山区的XCO2低于平原，但高于海洋。本文研究的平原地区是一个包括秦皇岛市的城区。前人的研究表明，不同的估算方法对该地区大气-海洋CO2通量的估算结果不同，但所有的方法都证实了渤海是冬季碳汇区，因此图6 的结果合理。图6（a）中黑点为正常的点数据，蓝点表示云层数据；图6（b）中蓝线为每10 s 对黑点滑动平均的结果。

图6 XCO2反演结果可视化Fig.6 Visualization of the XCO2 inversion results

检索了研究区域2019 年3 月14 日前后3 天的OCO-2 产品数据集，发现2019 年3 月14 日和16 日的XCO2产品可用。如图7 所示，OCO-2 在3 月16日的XCO2观测值与研究区比较接近，且数量较高。3 月16 日OCO-2 的XCO2波动在401.4×10-6～420.6×10-6，平均值为412.83×10-6。3 月14日，OCO-2 的XCO2波动在410.8×10-6～420.0×10-6，平均值为414.65×10-6。OCO-2 的XCO2反演结果表明海洋和陆地之间存在CO2梯度。除此之外，机载差分吸收激光雷达的XCO2与OCO-2 的XCO2存在明显的差异。机载差分吸收激光雷达的XCO2均值为416.26×10-6，而OCO-2 在3 月14 日和3 月16 日的XCO2均值分别为414.65×10-6、412.83×10-6。这些差异可以归结为以下原因：1）OCO-2 的XCO2与机载IPDA 激光雷达路径相比，OCO-2 的XCO2产物没有覆盖城市地区。人们普遍认为城市CO2高于郊区。2）相对于整个大气柱的XCO2，本文中机载差分吸收激光雷达观测的XCO2实际上只是部分XCO2。由于对流层低层的XCO2显著高于高海拔地区，因此机载差分吸收激光雷达观测的XCO2明显高于全部OCO-2 观测到的整个对流程的XCO2。另外，在基于差分吸收激光雷达观测的XCO2和OCO-2 卫星基于光谱仪观测的XCO2的比较中，存在一个非常复杂的问题。目前OCO-2/3、GOSAT-1/2、TanSat 等类似传感器的检索算法都是使用平均核来计算最终的XCO2。然而，双波长差分吸收激光雷达不产生平均核，而是直接计算柱加权的XCO2，因此，直接比较2 种产品存在问题。

图7 OCO-2 和路径积分差分吸收激光雷达XCO2的可视化Fig.7 Visualization of the OCO-2 and path integral differential absorption lidar XCO2

3 结束语

随着XCO2监测精细化需求的提高，卫星（如OCO-2/3、GOSAT-1/2 和Tan Sat）很难满足基于被动探测理论高精度、全天和全天候的需求。目前全球迫切需要开发主动探测卫星来支持全球碳源、碳汇和碳中和工作的开展。我国已经在2022 年4 月16 日发射大气环境监测卫星，该卫星配备了CO2路径积分差分吸激光雷达。星载差分吸收激光雷达在夜间以及高纬度地区和严重污染地区的有效观测方面可以补充目前被动遥感技术。尽管夜间、白天和季节的CO2排放主动传感、地球行星的高级空间碳和气候观测致力于填补该空白，但目前仍没有基于激光雷达的卫星在轨道上进行CO2探测。因此，完善机载（星载激光雷达的缩小原型）差分吸收激光雷达关键性技术开发，具有重要的科学意义。

基于该卫星的缩比机载实验，开展了相应关键算法技术的研究，其主要工作包括：1）提出了波形能量方程，针对差分吸收激光雷达信号非高斯性、复杂性和波动性，预先构建了波形能量方程，其方程较好地解决了信号非高斯问题；然后基于波形能量方程式，分别提取出了后续计算CO2浓度所需要的模型参数组。解决了参数多方程传递的问题，也有效降低了参数间接携带的误差。2）设计了差分吸收激光雷达信号模型参数优化方法，针对差分吸收激光雷达信号非高斯性的特点，结合传统的LM算法，通过替换LM 算法核心。有效地实现了波段on 和波段off 模型参数组的优化，为后续计算光学厚度提供精确的参数输入。3）设计了双探测误差消除方法，因为差分吸收激光雷达需对同一目标连续2 次距离测量，从而带来测量信息的冗余观测以及2 次测量结果相互不匹配的问题。将优化后的模型参数组的参数don和doff进行不等精度的直接平差，从而获取准确的参数d。为后续计算积分权重降低了很大的误差，从而间接的提高了CO2浓度的计算。4）模型算法进行了验证，通过在秦皇岛的实验，表明提出的模型在海上和陆地上的精度分别为0.74 和6.20 m。与1.572 μm 的差分吸收激光雷达空间分辨率1.2 m 相比，海面模型验证的精度表明，算法精度已进入亚单位。而以OCO-2 卫星的XCO2作为参考，本文算法可以得到趋势一致的XCO2。特别是在10 s 滑动平均值下，海洋、城市和山区的平均XCO2值分别为411.07×10-6、425.71×10-6、417.87×10-6，标准差分别为1.93×10-6、0.85×10-6、0.96×10-6。综上所述，该算法提高了XCO2反演的准确性和稳健性，对我国近年来即将发射的卫星搭载的差分吸收激光雷达具有重要的参考意义。