基于多模型级联的油浸式电力变压器故障诊断方法

李 元，李星辉，孙渭薇，李 睿，林金山，张大宁，张冠军

（1.西安交通大学电气工程学院，陕西西安 710049；2.国网陕西省电力有限公司营销服务中心，陕西西安 710075）

0 引言

油浸式电力变压器是电网中的关键设备之一，承担着电能传输、变换等关键任务，及时精确的变压器状态预警和故障诊断对设备智能运维和电网的运行安全都具有重大的意义[1]。油中溶解气体分析（Dissolved Gas Analysis，DGA）方法是目前变压器最可靠的故障诊断方法之一[2]。在变压器运行中会产生少量特征气体溶解于变压器的绝缘油中，当变压器内部发生故障时，部分气体浓度会急剧增加，因变压器内部故障产生的典型特征气体有氢气（H2）、甲烷（CH4）、乙烷（C2H4）、乙烯（C2H2）、乙炔（C2H2）等[3]。长期以来，以气体含量比值法为基础的DGA 方法在油浸式电力设备的状态监测与预警中都发挥了重要作用，经典比值法有三比值法（C2H2/C2H4，CH4/H2，C2H4/C2H6）[4]、Rogers四比值法（C2H2/C2H4，CH4/H2，C2H4/C2H6，C2H6/CH4）[5]和Duval 三角形法[6]等。比值法规则简单、应用广泛，但存在编码缺失、编码界限过于绝对等问题，可能导致状态无法确定或诊断错误，因此在实际应用中比值法存在不少局限性[7]。

随着人工智能技术的发展，机器学习方法被大量运用到变压器故障诊断领域，取得了不错的效果。常用的机器学习方法有人工神经网络（Artificial Neural Network，ANN）[8-9]、支持向量机（Support Vector Machine，SVM）[10-11]、K近邻（K-nearest Neighbor，KNN）[12]等，研究结果显示这些方法均有效克服了传统比值法的缺陷，在诊断精度和诊断效率方面均取得了一定的效果。

对于一个特定的应用问题，各智能分类器均能取得一定效果，但单个分类器很难取得全面优势，实际应用的综合表现欠佳。因此，有必要研究将多个不同分类算法的结果进行有机综合的方法，以获得整体更优结果[13]。变压器不同的内部故障在特征空间上往往有一定交叠，单一模型在分类不同故障时容易出现混淆，表现为对不同故障类型的识别准确率差异较大，对某些故障类型的识别率特别低（<60%）[14]，无法满足现场应用需求；另一方面，大部分诊断算法的内在逻辑是从不同的数据结构和数据空间角度观测数据，依据观测状况及算法自身的分类原理建立相应模型，所以不同的分类模型往往对同一故障类型的识别能力存在差异[15]。

为了能够充分融合单一分类模型的局部优势，进一步提升诊断效果，本文提出一种基于集成学习思想的双层级联变压器故障诊断模型：首先采用无编码比值方式提取油中溶解气体特征，增强不同故障类型的区分度；然后训练SVM、分类回归树（Classification and Regression Tree，CART），KNN 和朴素贝叶斯（Naive Bayes Classifier，NBC）4 种分类器作为第一级模型；第二级分类模型利用随机森林（Random Forest，RF）对前端多分类器的组合输出结果进行特征提取和识别，最终确定变压器的故障类型。

1 不同分类模型原理与性能评价指标

为了验证级联模型的有效性，选取SVM，CART，KNN 和NBC 4 种常见的分类模型作为级联模型的第一层并行分类器。SVM 广泛适用于油色谱故障诊断这类样本量小、非线性程度高、数据特征维数高的数据分类问题[10]；CART 模型在进行诊断时具有较高的诊断精度[12]；NBC 的逻辑性简单且无需设置参数，所以算法的表现也具有一定的健壮性[16]；KNN 由于其自身原理比较适合于油色谱故障诊断等类域交叉或重叠较多的数据分类问题[12]。以下简述四种故障分类模型的原理。

1.1 基于SVM的变压器故障诊断模型

SVM 来源于二维空间的求解最优线性分类面的问题，其主要目的是寻找一个能够准确区分所有样本数据的超平面。针对数据在低维空间不可分的问题，SVM 通过核函数将原始数据从低维空间映射到高维空间，对原样本空间数据不可分转化为特征空间中的线性可分求解分类超平面的问题。SVM在样本量小、非线性程度高、数据特征维数高的分类问题上有良好的表现。油色谱是一类具高维、线性不可分特征的数据，SVM 可以对油色谱表征的故障进行有效划分。超平面的求解过程如式（1）所示：

式中：w为分类超平面的法向量；Cp为惩罚因子；n为训练集样本数量；εr为第r个样本的松弛因子。

1.2 基于CART的故障诊断模型

CART 具有计算速度快、计算量小等特点，在处理小样本数据时具有较优的分类性能。CART 来源于人类的决策过程，是由节点和有向分支构成的树状层次结构。CART 的根节点是全体训练数据的集合。树的每一个叶节点都是一个节点分裂问题，产生的叶子节点是带有分类标签的数据集合，是样本的所属分类。CART 采用Gini系数作为节点分裂的属性依据，故障样本集S的Gini系数计算如式（2）所示：

式中：Pk为分类结果中第k个类别出现的概率。

对于含有N个样本的油色谱故障案例集合，将数据集划分为两部分，故障样本集S的属性A的第i个属性值的Gini系数的计算如式（3）所示：

式中：S1和S2分别为S二分类后的样本集；n1和n2分别为样本集S1和S2的样本数。

利用式（3），遍历样本集S的每一个特征的属性值，针对油色谱数据不断进行最优节点划分，最小值所对应的分类类型即为最终的诊断结果。

1.3 基于KNN的故障诊断模型

KNN 是一种通过不同数据特征值的距离进行分类的方法，主要原理是：如果一个待诊样本在特征空间内存在k个最近邻，那么预测样本的类别通常由k个近邻中的多数类别决定。对于连续型数据通常采用欧氏距离作为距离度量。在样本空间中不同样本点间欧氏距离计算de,f如式（4）所示：

式中：xeh，xfh分别为第e，f个样本点的第h维坐标。

在欧式空间中，针对每一个油色谱的故障样本点，依据欧氏距离求解其k个最近邻，则该样本点归属于k个最近邻的类别标签最多的一类。

1.4 基于NBC的变压器故障诊断模型

NBC 是一种简单有效的贝叶斯分类器，以贝叶斯定理为基础，求解在待诊故障样本出现的条件下各个故障类别出现的概率，最大概率项即为诊断结论。对一组训练集数据X={a1，a2…an}，设故障类别集合C={C1，C2…Cm}，NBC 分类模型会将X分配给Ci，当且仅当满足式（5）时，X∈Ci。

式中：Ci为第i个故障类别，Cj为第j个故障类型；m为故障类型的数量。

基于NBC 的变压器故障诊断模型是利用已经给定的油色谱故障数据集，求解每一类故障出现的先验概率，利用式（5）对其实现故障分类。

1.5 模型性能评价指标

事实上，每一种潜在缺陷、故障都可能引起严重后果，都应该引起足够的重视[17]。因此，一个性能优越的故障诊断模型应对各类故障都有较高的识别准确率。为了衡量单一分类器在不同故障类型上表现的差异性，引入变异系数（Coefficient Variation，CV）表征模型对不同故障类型识别效果的离散程度[18]。CV 越小，说明该模型对不同故障类型的敏感性差异越小。CV 的计算公式如式（6）所示：

式中：Ri为分类器对第i个故障的识别准确率；为分类器对所有故障的准确识别率的平均值。

针对多个分类器，引入Pearson 相关系数来衡量不同分类模型性能的差异性。Pearson 相关系数的绝对值越小，分类模型诊断性能的差异性越大[19]。为了能充分利用多分类器的局部优势，需要寻找具有较大差异的分类器组合来提高对每种故障类型的准确识别率，减小变异系数CV。Pearson 相关系数rxy由式（7）得到。

式中：R1i和R2i分别为2 个分类器对第i类故障的识别准确率；和分别为2 个分类器对所有故障的准确识别率的平均值。

2 多模型级联诊断

2.1 二级分类模型

第二级分类模型利用RF 融合前端多分类器。RF 是以决策树为基本分类器的集成学习模型[20]。对于待诊数据，决策树给出一条由根节点到叶节点的唯一路径来确定其分类。设有l个决策树，N个训练数据，对每个决策树，有放回地从N个训练数据中抽取M个数据来训练每一个决策树，最后由l个决策树的分类结果投票得到最终分类结果。RF算法具有不错的分类精度，在充分融合第一层各分类模型优势的同时具有较好的泛化能力。其泛化能力主要依靠两个随机过程得以保证：

（1）训练数据的随机性。训练单个决策树的样本是从数据集中随机抽取的，保证了对数据特征的广泛提取能力。

（2）节点分裂特征的随机性。构建决策树的特征值是随机选取，在对决策树每个节点进行分裂时，从全部属性中等概率随机抽取一个属性子集，再从这个子集中选择一个最优属性来分裂节点。

2.2 模型级联原理

为了吸收不同分类模型的优点，本文提出了一种模型级联框架，在级联模型训练完成后其对待诊油色谱数据的诊断流程如图1 示。

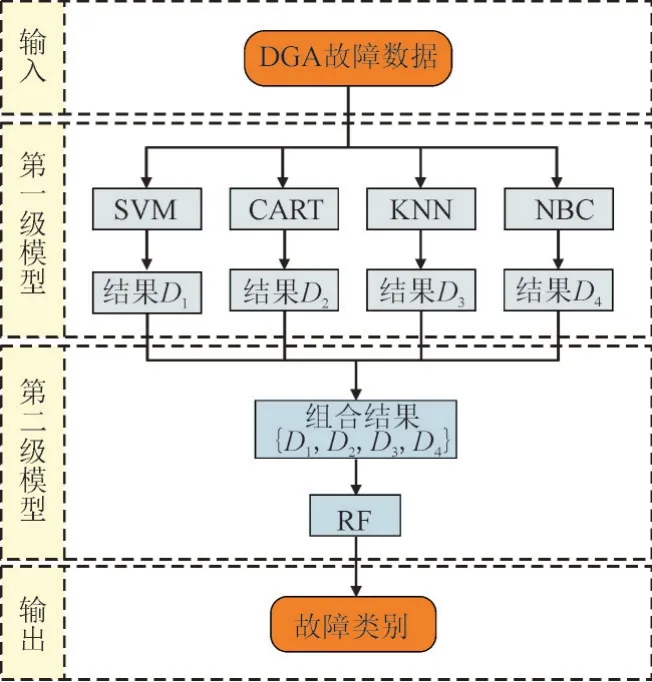
图1 级联模型诊断流程Fig.1 Diagnostic process of cascade model

第一级模型中的每个基分类器独立对油色谱数据进行诊断，得到各基分类器的诊断结果Di（i=1，2，3，4），并对其组合得到故障类型编码向量D={D1，D2，D3，D4}；第二级模型对该向量再次进行诊断，来得到最终的诊断结果。

图1 所示的诊断过程建立在级联模型充分训练的基础上，级联模型具体的训练过程如下：假设有n个训练样本，诊断模型第一级中有4 个基分类器，为了保证诊断模型的泛化能力，首先将原始的训练集进行K折交叉划分得到K个子集{S1，S2…SK}；对第一级中的各分类器，将每个数据子集Sp（p=1，2…K）做一次测试集，其余子集做训练集，得到K个诊断子集Lp（p=1，2…K），Lp为Sp中样本诊断后得到的故障类型编码；将K个诊断结果子集合并成一列得到一个分类器对训练集中所有样本的诊断结果集合Et={L1T，L2T，L3T…LkT}T（t=1，2，3，4），该集合是一个n×1 的向量；针对每一基分类器分别进行一次上述操作，将每一个基分类器得到的结果Et进行组合得到一个n×4 的诊断结果集合E={E1，E2，E3，E4}，将E作为第二级分类模型的输入数据进行训练；再利用m个样本对第一级分类模型进行训练，将训练好的第二级分类模型与第一级分类模型按图1 所示级联。这种方式可以抑制多个分类器诊断的不平衡性，提升整体诊断效果。

3 诊断模型

3.1 特征提取与数据预处理

不同的编码方式可以提取油中溶解气体的不同数据特征，提取的油中溶解气体特征越丰富，越有利于提高诊断精度。杜洋等[21]提出了一种无编码比值的变压器诊断方法，包含9 个维度特征，即CH4/H2，C2H2/C2H4，C2H4/C2H6，C2H2/（C1+C2），H2/（H2+C1+C2），C2H4/（C1+C2），CH4/（C1+C2），C2H6/（C1+C2），（CH4+C2H4）/（C1+C2），其中C1+C2为油中溶解气体中总烃的含量。利用这9 种比值作为分类模型的输入数据，由于五种特征气体浓度差异性较大，直接将比值作为训练数据输入会对诊断效果产生不利影响[22]，需要依据式（8）对气体的特征比值进行归一化处理。

式中：cact为该故障样本的一种气体浓度比值；cmax为该种气体浓度比值的最大值；为该气体浓度比值归一化以后的值。

3.2 故障状态编码及诊断模型构建

根据IEC60599 标准[23]，变压器故障类型可划分为局部放电PD、低能放电LD、高能放电HD、低温过热LT、中温过热MT、高温过热HT 6 种，其对应故障类型依次编码为1，2，…6。

为了保证模型的泛化能力，将所有数据按照4∶1 的比例划分为训练集和验证集，再对训练集采取五折交叉划分，按照2.2 节所述方法训练第一级和第二级模型，得到最终的诊断模型。完整的级联模型数据预处理、参数训练与自优化过程如图2 所示。

图2 变压器级联故障模型详细运作过程Fig.2 Diagram showing data preprocessing，parameter training and self-optimizing process of cascading fault model for transformer

4 案例验证

4.1 数据划分

本文模型建立所用的506 例DGA 故障数据均来源于电网公司故障变压器的油中溶解气体离线试验数据，按照3.1 节所述方法进行特征提取和归一化处理，依据3.3 节所述方法进行训练集和验证集划分，样本分布情况如表1 所示。

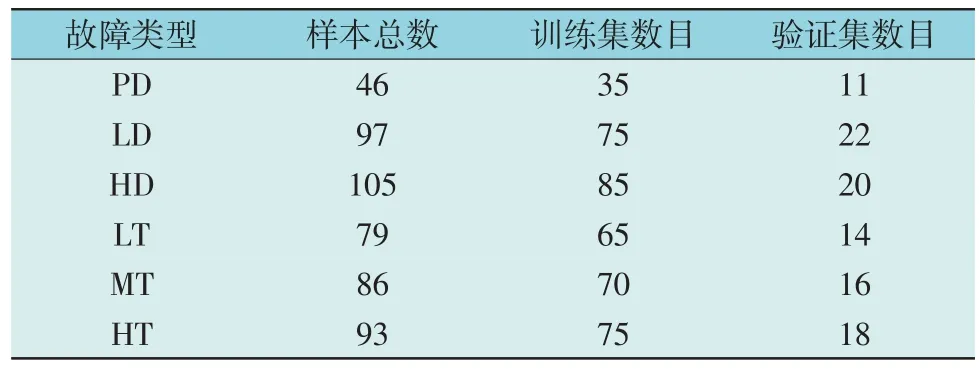
表1 506组故障样本数据分布Table 1 Distribution of 506 groups of fault samples

4.2 基分类器诊断结果分析

利用2.2 节中所述方式对4 种基分类器进行训练，利用得到的模型在验证集上进行测试。第一级模型各分类器参数如表2 所示。利用验证集对训练得到的模型进行测试得到的结果如表3 所示。

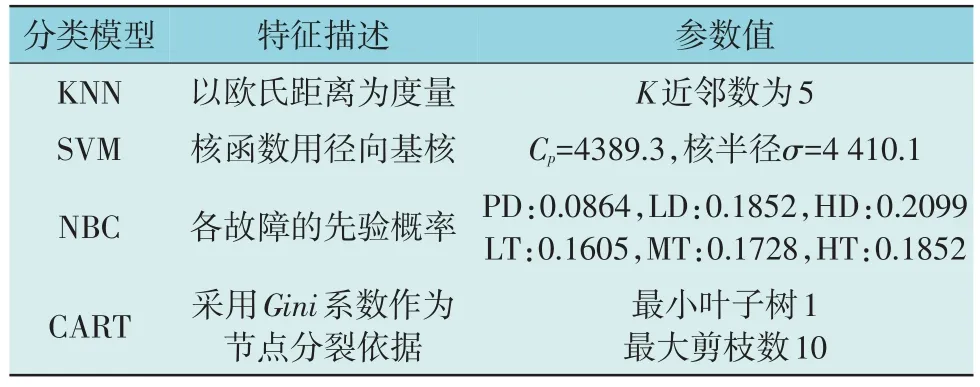
表2 第一级模型各分类器参数Table 2 Parameters of each classification model at the 1st layer

表3 第一级模型对不同类型故障的识别准确率对比Table 3 Comparison of recognition accuracy among classification models at the 1st layer for different fault types%

由表3 可知，不同分类器对不同故障类型的识别能力差异较大。以局部放电放为例，KNN 模型和NBC 模型具有最高的准确识别率，达到了81.82%，而SVM 和CART 的表现较差，准确识别率仅为45.45%和55.45%。为了分析第一层各分类模型的差异性，根据式（7）及表4 计算第一层各分类模型间的Pearson 相关系数rxy，各模型之间相关系数的绝对值如图3 所示。

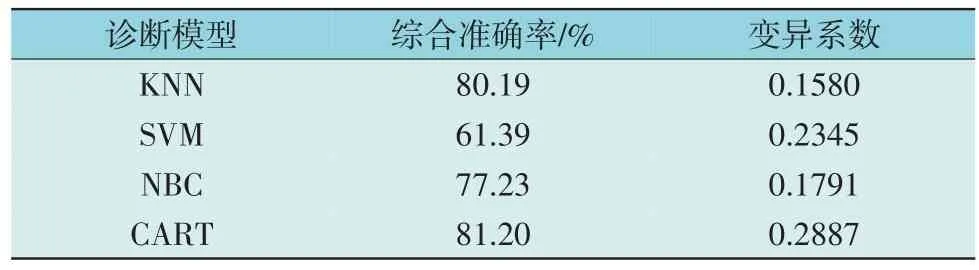
表4 第一级分类器综合诊断结果对比Table 4 Comparison of comprehensive diagnosis results among classification models at the 1st layer

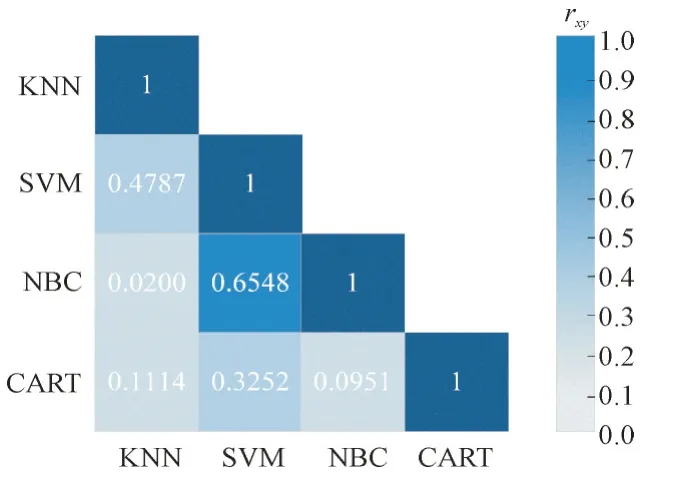
图3 基分类器间的Pearson系数rxyFig.3 Pearson coefficient rxy between base classifiers

一般认为，|rxy|<0.3，两变量基本不相关，基分类器的性能相似度低，诊断结果融合效果好；0.3≤|rxy|<0.5，两变量低度相关；0.5≤|rxy|<0.8，可认为两变量中度相关；|rxy|≥0.8 时，两变量间高度相关，此时两基分类器表现极度相似[23]，将其融合无法起到抑制基分类器不平衡性的作用，需要更换分类器。由图3 可知，本文第一级分类器中所选的4 种模型彼此之间的相关性均不超过0.8，因此融合之后可以充分吸收不同模型的优势，抑制单一模型诊断的不平衡性。

一级分类器综合诊断性能对比如表4 所示。总体而言，CART 的综合识别准确率最高（81.2%），但其变异系数也最高，说明CART 对不同故障类型的识别差异性很大。KNN 的综合识别准确率要低于CART，但变异系数要明显小于CART。所以，4种模型各有优势，有必要对其充分融合利用。

4.3 级联模型诊断结果分析

将第一层分类模型的诊断结果组合输入到第二层分类模型中，得到最终的级联诊断模型。第二层分类模型训练得到的参数为子树数目20。

利用验证集对级联模型进行测试，级联模型与第一级中的基分类器对不同故障类型的准确识别率对比如图4 所示。

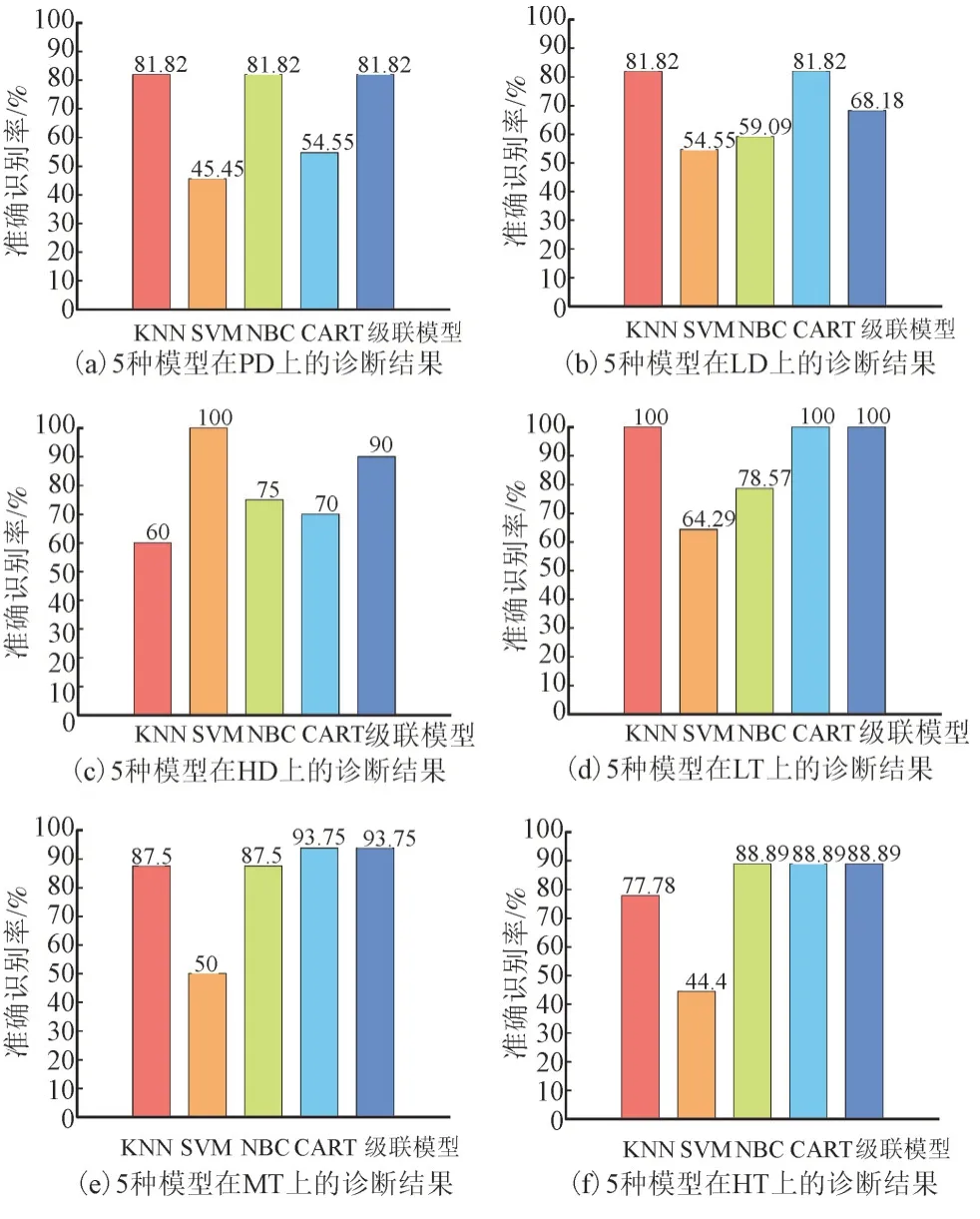
图4 5种模型对不同变压器故障类型的识别准确度对比Fig.4 Comparison of recognition accuracy among five models for different transformer fault types

级联模型在每一种故障类型上的效果都达到了基分类器的最优或较优水平，有效地抑制了基分类器的不平衡性。以PD 和HT 为例，级联模型对PD 识别准确率为81.82%，与KNN 与NBC 相当，高于SVM（45.45%）与CART（54.55%）；级联模型对HT 的识别准确率（90%）略低于SVM（100%），显著高于KNN（60%）、NBC（75%）和CART（70%）。5 种模型的综合识别准确率和变异系数对比如图5 所示，级联模型在两个综合评价指标上均取得了最好效果，其综合识别准确率比四种单一模型分别提升了6%、24.8%、8.96%、4.99%，变异系数分别降低了0.0024、0.0789、0.0235、0.1331，验证了级联模型的有效性。需要注意，本文中所述单一诊断模型和级联诊断模型对算力的需求不高，数秒即可完成诊断，实效性满足现场应用需求[24]。

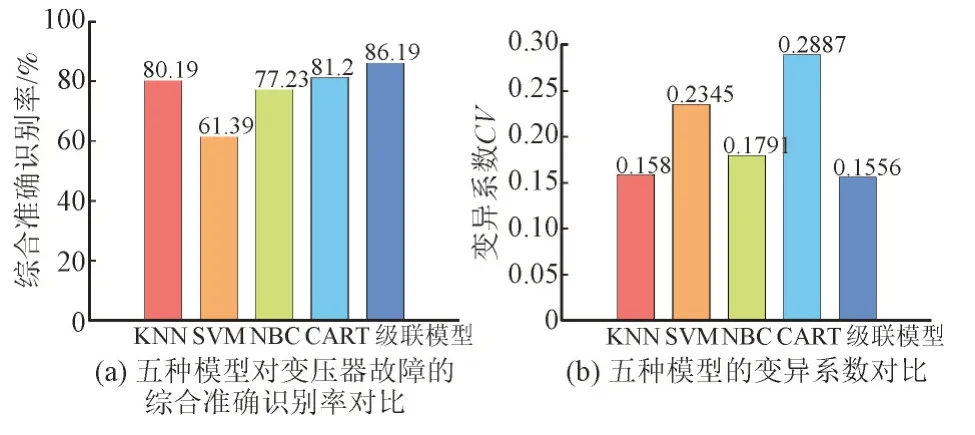
图5 五种模型的综合评价指标对比Fig.5 Comparison of comprehensive evaluation index among five models

5 结论

针对在变压器故障诊断中，单一分类模型对不同类型故障时诊断效果的不平衡性，以及不同单一模型之间分类性能的差异性等问题，本文提出了一种双层级联的变压器故障诊断模型，可充分吸收单个模型的优势，进一步提升对变压器的故障诊断效果。结合案例分析得到的具体结论如下：

1）针对变压器的6 种故障类型，级联模型的表现总是处于第一级4 个分类模型的最优或次优水平，缓解了单一诊断模型的不平衡性。

2）在综合准确识别率以及变异系数两个综合评价指标上，级联模型的表现都优于单一模型，证明了其有效性。