改进灰狼算法在含风电的配电网无功优化中的应用

夏正龙，陆良帅，吴启凡，李 灿，陈 宇

（江苏师范大学电气工程及自动化学院，江苏徐州 221000）

0 引言

能源是一个国家发展的基本推动力，随着国家的快速发展，可再生能源成为长久发展的持续动力[1]。风力发电因其波动性，是电力系统中的薄弱环节，其无功缺陷将引起电网电压的剧烈波动，严重时还会引起电网解列[2]。由于风电场的接入改变系统的潮流分布，使网络中的无功潮流发生变化，导致某个节点的无功不足或过剩[3]，因此为了降低配电网损耗[4]，提高系统稳定性对含风电场的配电网无功优化研究具有非常重要的意义。

在最佳无功补偿点的选择上，文献[5]通过电压稳定模态分析法确定无功装置安装节点，再使用模糊权重法建立无功优化模型。风力发电具有分布性、随机性及不确定性等特性[6-7]，这种随机性对配电网的稳定有很大影响，对于风力发电出力不确定性的处理方式有两种：场景分析法[8]和分时段优化法[9]，场景分析法是将风机输出功率分为：额定输出功率、停机输出、欠额定输出，使得随机的风机出力变为简单的3 个场景；分时段优化法将优化问题分解为多个时段，并分别对每个时段进行优化。

电力系统无功优化是一个多约束、多变量的非线性问题[10]，常用的算法传统优化算法与智能优化算法有两种，而含风电场的配电网无功优化以智能算法[11]为主。文献[12]提出了一种基于改进天牛须算法的含固态变压器的配电网无功优化方法，对含固态变压器的配电网进行无功优化，使系统的电压偏差与功率损耗达到最小。文献[13]将粒子群算法（Particle Swarm Optimization，PSO）应用到IEEE6 节点模型的无功优化中，但未进行算法的改进提升，优化模型也较为单一。文献[14]针对传统方法得到的帕累托边界多样性差的问题，提出一种改进的多目标粒子群优化算法。并将改进的粒子群算法应用到含风电IEEE33 节点系统无功优化中，验证了改进算法的优越性。研究表明灰狼算法（Gray Wolf Optimization，GWO）在函数优化上，收敛精度与求解精度均优于PSO[15]。文献[16]对算法的改进方法引用了混沌理论，利用混沌算子在最优解邻域进行搜索，提高了算法的全局搜索能力。而文献[17]在引入混沌种群初始化后，并且引入差分算法的交叉变异来提高对最优解的全局搜索能力。传统函数需要对目标函数的解析性质有明确要求，知道目标函数的精确表达式，而智能优化算法则不需要这些[18-20]。

在考虑双馈风电场的波动性与无功调节能力基础上建立以系统有功网损最低为目标函数，并兼顾配电网与双馈风机自身约束条件的无功优化模型；利用MATLAB 软件对双馈风机接入的IEEE33 节点系统模型进行无功优化仿真分析，验证改进的灰狼算法（Improved Gray Wolf Optimization，IGWO）在求解含有风电场的配电网无功优化问题上的优越性。

1 配电网无功优化数学模型

1.1 双馈风机无功极限

双馈风机具备独立的无功调节能力可实现功率的解耦控制[21]，双馈风机的无功输出主要是由定子侧与网侧变流器决定的，双馈风机定子端功率在电网电压定向同步d-q坐标系下的表达式为：

式中：ug为定子电压即网侧电压；iqs，ids分别为定子电流d-q轴分量。

由式（1）结合定转子电流间关系式，可得：

式中：ird，irq分别为电机转子d-q轴电流分量；Us为定子电压；Lm为双馈风机定转子间的互感；Ls为定子电感；ω1为双馈风电机组同步转速。

由式（2）可知双馈风机定子侧有功无功功率主要由机端电压、定子转子绕组参数和转子侧的电流决定，因其它参数在运行中为定值，故定子侧有功无功功率受转子侧变换器电流限制，由此可得：

因此对于给定有功功率Ps的情况下，定子无功功率的范围为：

式中：Qsmax，Qsmin分别为双馈风力发电机定子侧的无功最大输出值与最小输出值。

式中：Xs，Xm分别为定子电抗与励磁电抗。

1.2 分时段策略

由于风速的随机性与波动性，需要将风电场功率输出不确定的动态问题转化为确定的静态问题。为了使含风电场配电网的无功优化效果更好，本文采取了分时段策略。该策略是将风电场中随时间波动的风速在一段时间内通过积分运算等效成在该段时间内匀速的风速：

根据式（6）可以计算出每个时段的平均风速，再由风力发电机组的功率特性曲线得到每个时段风力发电机的有功输出。有功功率输出为定值后，由式（5）可以计算出风机的无功极限。6 台额定功率为1.5 MW 双馈风机在不同风速下的功率输出如表1 所示。

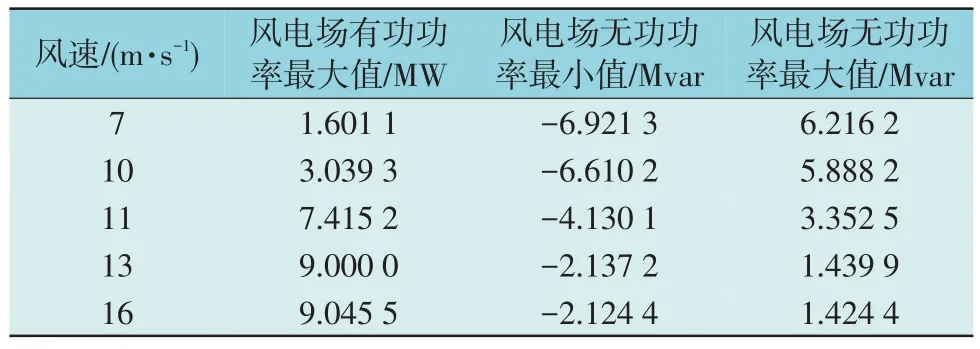
表1 6台双馈风机在不同风速下的功率输出Table 1 Power output of six doubly-fed wind turbines under different wind speeds

1.3 无功补偿节点

随着风电并网后结构变得复杂[22]，为解决风电并网后的动态问题。因此选择最佳的无功补偿点较为重要，本文使用灵敏度分析法选择最佳的无功补偿节点。

系统的有功网络损耗可表示为[23]：

式中：Ploss为系统的有功网络损耗；n为风电场内节点数；Gij为节点i，j之间的电导；Ui为节点i的电压幅值，Uj为节点j的电压幅值；θij为节点i，j间的电压相角差值。

有功网损灵敏度计算公式如下：

式中：Q为配电网的无功功率；U为配电网的节点电压幅值；θ为相角大小。

将式（8）进行如下处理：

所以得到配电网有功网损无功灵敏度矩阵计算公式为：

式中：SPloss-Q为雅可比矩阵逆矩阵的子阵。

将系统在i节点处的有功网损对电压以及相角求偏导，如下所示：

利用式（11）可在IEEE33 节点系统模型中编程，得到图1 所示的最小无功补偿灵敏度的节点图，根据图1 选择3，6，18 节点作为无功补偿节点，在这3 个节点安装静止无功补偿装置。

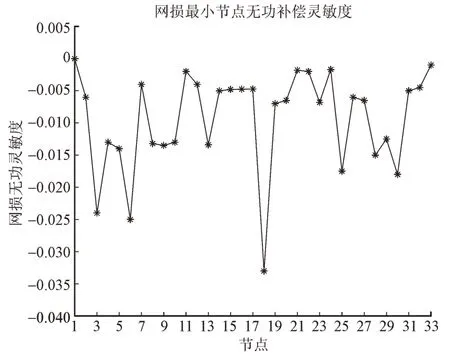
图1 网损最小节点无功补偿灵敏度Fig.1 Reactive power compensation sensitivity at node with minimum network loss

1.4 目标函数

电力系统无功优化目标函数的选取，需要综合考虑系统的电能质量和经济效益，以寻求最优的调节方案，提高电力系统的运行效率和经济性，因此本文以有功功率损耗最小为目标函数。假设系统有n个节点，m条支路，则目标函数为：

式中：Gij为节点i，j之间的电导；Ui为节点i的电压幅值；Uj为节点j的电压幅值；θij为节点i，j间的电压相角差值。

1.5 约束条件

在含风场电配电网无功优化模型中，约束条件包含等式约束条件与不等式约束条件。

1.5.1 等式约束条件：

式中：Pi，Qi为节点i的有功功率和无功功率；Gij，Bij为节点i，j之间的导纳。

1.5.2 不等式约束条件：

节点电压约束条件：

风电机组吸收无功功率约束条件：

补偿节点无功补偿容量约束条件：

有载调压变压器变比约束条件：

式中：Uimax，Uimin为节点i的电压的上下限值；QGimax，QGimin为风电机组无功出力上下限值；QGi为风电机组i的无功功率值；QCimax，QCimin为无功补偿节点i的无功补偿容量上下限值；QCi为节点i的补偿容量；Timax，Timin为有载调压变压器变比的上下限值；Ti有载调压变压器的变比。

2 改进灰狼算法

2.1 标准灰狼算法

GWO 模拟了自然界灰狼的领导和狩猎层级，在狼群中存在4 种社会等级，如图2 所示按照等级从高到低分别是α狼、β狼、δ狼和ω狼。

图2 灰狼社会阶层图Fig.2 Diagram showing social class of gray wolf

其寻优原理如下：

1）包围猎物。在寻找猎物过程中，将灰狼围捕猎物的行为定义为：

式中：D为距离向量；A和C为行为系数向量；XP为猎物的位置向量；X(t)为迭代次数为t时的灰狼的位置向量；t为算法当前的迭代次数；系数向量A和C→的公式为：

式中：a为收敛因子，随着迭代次数从2 线性减小到0；tmax为最大迭代次数；r1和r2为区间[0，1]内随机数。

2）狩猎。灰狼对猎物的识别能力较强，且在领头狼识别猎物后，其它狼都由领头狼带领，即灰狼的位置更新是根据领头狼的位置来探索与更新。

灰狼个体跟踪猎物的数学模型如下所示：

式中：Dα，Dβ，Dδ分别为α,β,δ与其他个体之间的距离向量；Xα，Xβ，Xδ分别为α,β,δ的当前位置向量；C1，C2，C3为随机向量；X为当前灰狼位置的向量。

式中：X1，X2，X3为三个头狼对狼群个体ω的位置更新扰动。

式（25）分别定义了狼群中个体ω在α狼、β狼、δ狼指挥下前进的步长和方向，式（26）定义了ω的最终位置。

2.2 灰狼算法的改进

本文对传统灰狼算法做出如下4 点改进。

2.2.1 混沌反向学习初始化

Logistic 映射就是一种典型的一维混沌系统，具有极其复杂的动力学特征，它的数学表达式为：

式中：z(t) 为混沌域，z(t)∈（0,1）且z(t)∉（0.25,0.5,0.75）；μ为Logistic 映射参数，且μ∈（0,4）为一个常数。

式中：am，bm为xm的边界；m为粒子个体。

将混沌映射和反向学习结合应用在初始化，先利用Logistic 混沌映射产生N 个初始解，然后每个初始解按照如下方式产生相应的反向解：

式中：为每个初始解Xi所对应的反向解；K为[0，1]内的随机数；Xmax，Xmin分别为所有初始解中每维向量的最大值和最小值。

2.2.2 改进非线性收敛因子策略

由式（21）和式（22）可知，收敛因子a的变化影响系数向量A的变化，但收敛因子a随着迭代次数的增加从2 线性递减到0。线性递减的收敛因子a使得GWO 在搜索过程中不能兼顾全局与局部搜索能力，为了增强GWO 的全局与局部搜索能力，本文提出的改进公式如下：

式中：tmax为最大迭代次数；k为调节参数。

2.2.3 自适应个体记忆策略位置更新

2.2.4 柯西变异

按照式（19）和式（20）的搜索方式容易陷入局部最优，为了使算法前期搜索更加充分，本文在算法中引入了柯西变异算子，来提升>1 时的全局搜索能力。柯西异变基于柯西概率密度函数，如式（33）所示：

本文中t取1，为标准柯西分布。将其与灰狼算法的位置更新公式相结合，帮助算法跳出局部最优，其具体表达式为：

2.3 改进GWO流程图

改进灰狼算法优化含风电场配电网无功优化流程图如图3 所示。

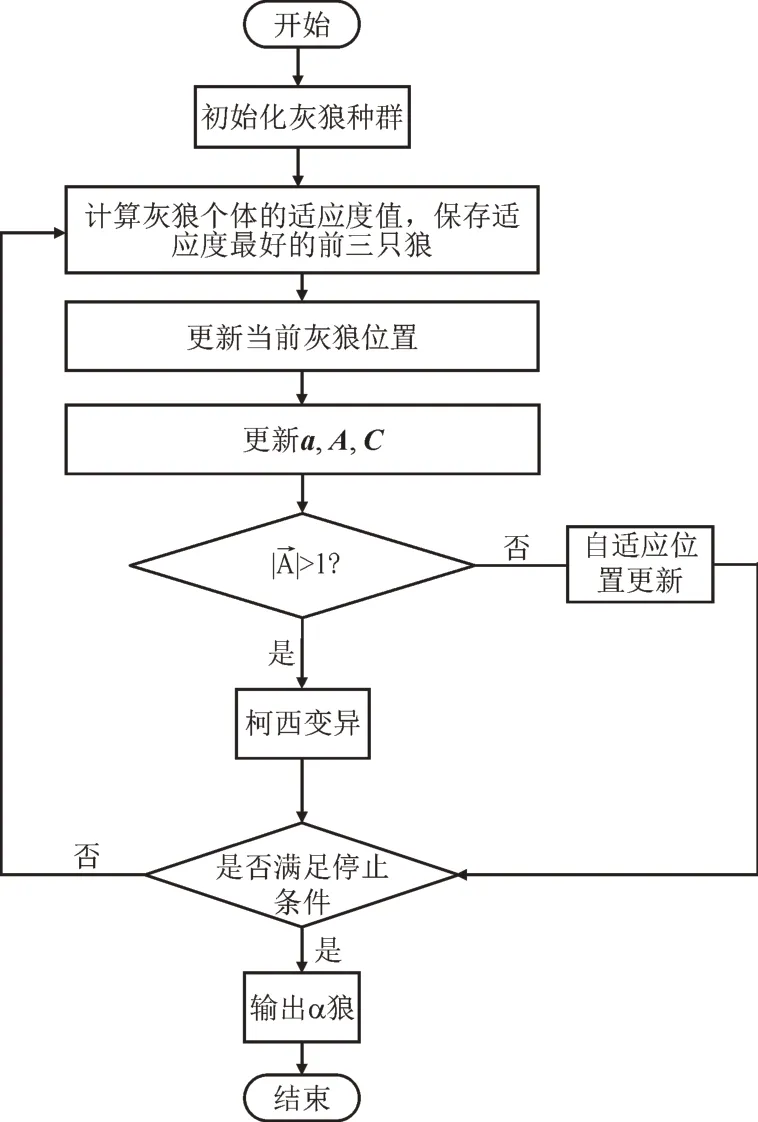
图3 改进灰狼算法流程图Fig.3 Optimization flowchart of improved gray wolf algorithm

3 算例分析

3.1 基本参数

本文利用改进灰狼算法对改进的IEEE33 节点进行无功优化测试，改进的IEEE33 节点系统模型，如图4 所示。

如图4 所示双馈风电场设置在19 节点处，其中包括6 台1.5 MW 双馈风力发电机组，组成一个装机容量为9 WM 的双馈风电场节点，双馈风机额定电压为690 V，其它电气参数如表2 所示，各变量约束范围如表3 所示。无功补偿节点为3，6，18。GWO 与IGWO 参数设定灰狼种群为50，迭代次数为50，维度设定为3；PSO 的种群数量为50，惯性因子ω的上限为0.6，学习因子c1，c2均为2.01，迭代次数为50，维度设定为3。

表2 风力发电机参数Table 2 Parameters of wind turbine Ω

表3 变量约束范围Table 3 Variable constraint

3.2 静态无功优化分析

在不考虑风速波动影响，将风速视为额定风速下，图5 是PSO，GWO 和IGWO 运行30 次后求平均值得出的收敛曲线图，从图5 中可以看出改进灰狼算法的收敛速度比标准灰狼算法和粒子群算法更快，在收敛精度方面可以看出3 种算法收敛精度相似，但是本文算法收敛精度较好，说明IGWO 算法搜索到全局最优的能力得到加强。在寻优效率方面，本文算法迭代次数远少于其它2 种算法，耗时更短寻优效率更高。

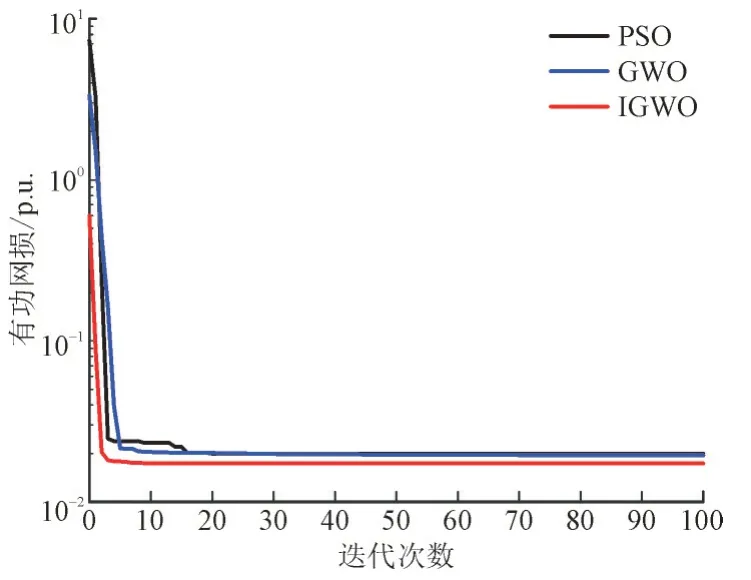
图5 3种算法的收敛曲线Fig.5 Convergence curves for three algorithms

图6 为优化前后的各节点电压曲线图。

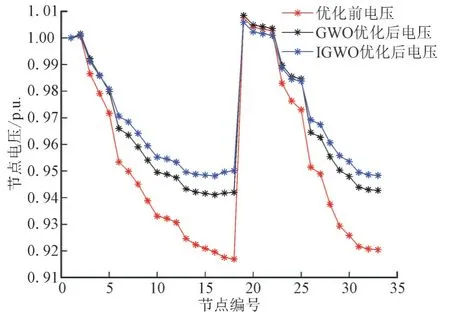
图6 优化前后的各节点电压曲线图Fig.6 Voltage curves of each node before and after optimization

由图6 可以看出，优化后的节点电压变化幅度明显降低，电压质量有所提升。对比IGWO 算法与GWO 算法优化后电压，说明通过IGWO 智能优化算法得出的无功补偿方案可以更有效地提高电压，减少电压的波动。

3.3 动态无功优化分析

现实中的风速都是具有波动性的，波动的风速导致功率输出也是波动的，为了提高优化效果，本文兼顾它们的变化性与优化的可行性采用分时段策略，将1 d 24 h 分为5 个时间段，对每个时间段单独优化。

3.3.1 各时段下节点电压

图7—图11 是第1—第5 个时间段各节点电压。

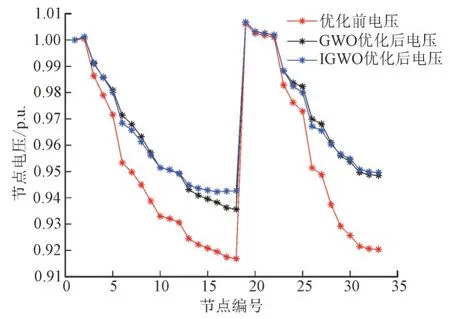
图7 第1个时段下各节点电压Fig.7 Each node voltage in the first period

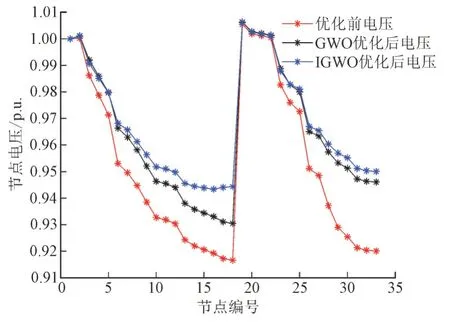
图8 第2个时段下各节点电压Fig.8 Each node voltage in the second period

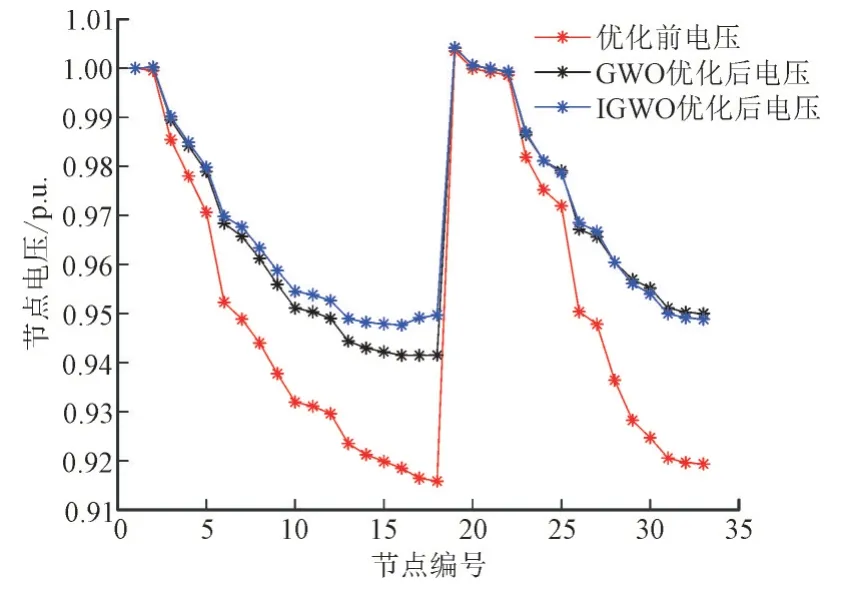
图9 第3个时段下各节点电压Fig.9 Each node voltage in the third period

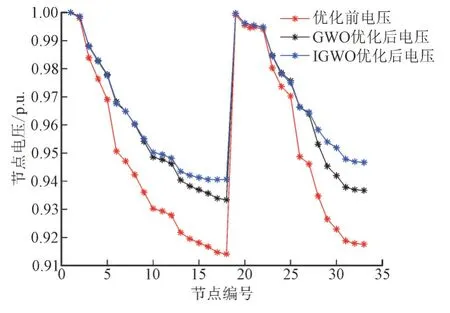
图10 第4个时段下各节点电压Fig.10 Each node voltage in the fourth period

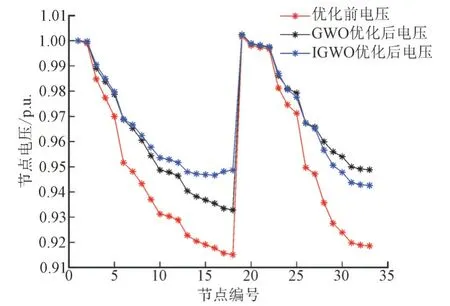
图11 第5个时段下个节点电压Fig.11 Each node voltage in the fifth period

从各时段节点电压图中可以看出，优化后的电压明显优于未优化的电压，且IGWO 优化后的电压整体上比GWO 优化后的电压更稳定。

3.3.2 各时段下系统网损

优化前后系统各时段的网损如图12 所示。

图12 优化前后系统各时段的网损Fig.12 Network loss of system in each period before and after optimization

由图12 可以明显地看出风电场接入后损耗明显增加且变的波动，但无功补偿优化后系统的网损明显下降，且IGWO 优化后的网络损耗整体上比GWO 优化后的网络损耗更低，证明本文提出的改进算法与GWO 相比具有优越性且本文提出的无功补偿方案是有效的。

4 结论

针对风电场并网易造成电网电压波动和线损增高的问题，以最小网损为目标函数，将无功补偿容量作为控制变量，对双馈风机接入的IEEE33 节点系统进行仿真分析，结果证明：

1）对于风速与功率的波动性问题，本文的分时段策略将1 d 24 h 分为5 个时段，相比静态优化具有较好的优化效果。

2）针对GWO 求解精度低、收敛速度慢、易陷入局部最优等现象，在其基础上结合混沌反向学习、柯西变异、非线性收敛因子及自适应个体记忆策略，有效提升了算法的收敛速度与收敛精度，验证了算法改进的有效性。