构建指向活动经验积累的数学学习

莫正云　朱成星

【关键词】小学数学；生活经验；操作经验；探究经验；建构经验

【中图分类号】G623.5  【文献标志码】A  【文章编号】1005-6009（2023）22-0075-03

《义务教育数学课程标准（2022年版）》明确指出，要使“学生通过数学课程的学习，掌握适应现代生活及进一步学习必备的基础知识和基本技能、基本思想和基本活动经验”。帮助学生积累数学活动经验是数学教学的重要目标。本文以苏教版三下《小数的初步认识》一课的教学为例，谈谈如何在小学数学教学中促进学生积累活动经验。

一、唤起生活经验，感知小数读写

师：数学学习离不开数，我们已经认识了1、2、3、100、1000等整数，还学习了分数，今天我们来认识小数。

师：你在哪里见过小数？

生：超市商品价格、温度计……

师：老师也带来了一些生活中的小数，想去看看吗？

出示橡皮价格0.3元、身高1.3米、体温36.5摄氏度等。让学生尝试读小数，并互相纠正。

师：仔细看，这些小数的样子有什么特点？你会写出小数吗？

首先，从学过的“数”中引出整数、分数以及本节课要学习的小数，让学生感受小数不是孤立的；接着，从生活情境中的小数入手，让学生尝试读、写，并认识小数各部分名称。熟悉的生活场景使得学生为探究小数含义做好了心理铺垫和知识准备。

二、调动操作经验，初步理解小数

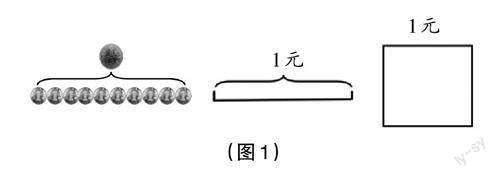
师（出示图1）：如果把下面每个图形看作1元，你能在图上分别表示出0.3元吗？

学生在不同图形中表征0.3元，并展示。

师：说一说，你是怎样想的？

生1：实物图1元=10角，3角就是0.3元。

生2：线段图把1元平均分成10份，其中的1份就是0.1元，3份就是0.3元。

师：为什么想到平均分成10份？

生2：因为1元=10角，平均分成10份，其中的1份就是0.1元，3份就是0.3元。

生3：正方形图把1元平均分成10份，涂出其中的3份就是0.3元。

师（课件展示三种分法）：图形不同，分法也不完全一样，为什么涂色表示都是0.3元？

小结：虽然图形不同，分法也不完全一样，但都是把1元平均分成10份，表示其中的3份，这让我们联想到以前学过的哪个分数？

生：[3/10]，0.3元就表示[3/10]元。

师：刚才，我们在不同的图上都找到了[3/10]元和0.3元。你还能在正方形图上表示出0.5元吗？还能找到其他小数吗？

师：观察板书，你有什么发现？

生： 十分之几元写成小数就是零点几元，零点几元就表示十分之几元。

師：在这个正方形里可以找到很多小数和对应的分数，根据涂色依次数下去，0.1、0.2、0.3、0.4……（学生数）如果继续涂下去，全部涂满就是整数1，1元里面有几个0.1元？10个0.1元是多少？10个1元是多少？10个10元是多少？

生：1元里有10个0.1元，10个0.1元是1元，10个1元是10元，10个10元是100元。

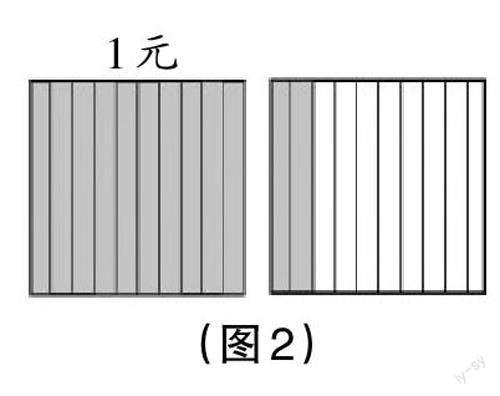
师：继续往下涂呢？（出示图2）现在表示多少元？为什么？（板书：1.2元）1.2元也是小数，它跟零点几元有什么不同？

仅凭生活经验，学生对0.3元的理解仍然停留在感性层面，对其本质含义的理解是模糊的。因此，本环节充分放手让学生在三种不同的图上表征0.3元，不仅让学生在不同量中感悟零点几元的含义，更在累加数数的过程中体会整数与小数的关联，零点几的小数跟学过的整数一样也是十进制关系。整个过程有挑战也有趣味，推动学生在动手操作、讨论归纳、思考比较、体验感悟中有效实现了对小数意义的初步建构。

三、迁移探究经验，加深本质理解

课件出示一条表示1米的线段。

师：一个正方形、一条线段可以表示1元，还可以表示什么？如果用这条线段表示1米，你还能像刚才那样在图上找出0.1米吗？

生：把1米平均分成10份，1份就是[1/10]米，写成小数就是0.1米。

师：在表示1米的线段上，除了能找到0.1米、[1/10]米，还能找到哪些小数和对应的分数？

学生回答，同时课件展示。

师：借助这条表示1米的线段，我们进一步理解了小数。无论是零点几元，还是零点几米、零点几分米、零点几千克，这些表示零点几的一位小数都表示十分之几。

师：如果要表示出1.3米，怎么办？如果要表示出2.8米呢？

生：在1米后面再接上同样的一段、两段，把每一段平均分成10份。

根据学生的回答，课件展示（如图3）。

借助直观的线段图，将小数与分数以及整数再次关联起来，学生在不断思考和表达的过程中，既有原操作经验的迁移，也有新探究经验的积累，对小数的理解也更加深刻。同时，线段图的呈现既是米尺模型的抽象和延伸，也为后续学习中将其抽象为数轴做好了准备。

四、拓展建构经验，完善认知结构

师： 如果把这条线段两端延展下去，你觉得像我们数学上的数轴吗？数轴下面的数0、1、2、3等是自然数，自然数都属于整数，而在整数之间又会有许多小数，表示零点几的小数在哪两个数之间？表示一点几的呢？表示十点几的呢？

生：表示零点几的小数在0和1之间，表示一点几的小数在1和2之间，表示十点几的小数在10和11之间。

师：明明身高1.3米，1.3在哪两个数之间？军军比他高一点，请你猜一猜，军军有多高？

学生自由猜想后，教师提示“大了”“小了”，直至逼近正确答案，课件出示军军身高1.36米（如图4）。

师：1.36在数轴的什么位置？怎样才能准确找到？

生：在1.3和1.4之间，把1.3和1.4之间再平均分成10份。

师：1.36跟我们今天学的小数有什么不同？

生：今天学了一位小数，1.36是两位小数。

师：是啊，我们以后会进一步学习两位、三位等多位小数，探究它们的含义。

数学知识具有高度抽象性，数学学习的魅力就在于能够促进学生实现从形象思维到抽象思维的飞跃。前面几个环节更多是操作经验、探究经验的呈现，到这里便更多是帮助学生积累思考的经验，把今天所学的小数纳入自己已有的关于数的认知结构中，促进他们实现结构化思考的经验积累和习惯养成。

总之，指向活动经验积累的数学学习更具力量。学生在整个学习过程中呈现了不同层次的原有经验，同时又获得了新的数学活动经验，形成了较为完整的认知结构，这些经验必然会对其后续的学习和发展产生积极的影响。