高中生数学建模素养的评价研究

◎ 汪 健

自《普通高中数学课程标准（2017 年版）》（以下简称《2017 版课标》）将“数学建模”作为数学学科六个核心素养之一提出以来，广大高中数学教师对数学建模的关注日益增加。《普通高中数学课程标准（2017 年版）解读》指出：“数学建模进入高中课程，就是要通过教师有目标、有层次的学习活动的设计和指导，影响学生的学习过程，改变传统的学习方式，引导学生主动、自主地学数学、做数学、用数学。”［1］而作为数学教学的一个有机组成部分，教学评价在数学核心素养各个维度的发展过程中起着举足轻重的作用，数学建模也不例外。因此，对数学建模的评价进行研究是重要且必要的工作。

《2017 版课标》指出，教学评价要遵循以下四个原则：重视学生数学学科核心素养的达成；重视评价的整体性与阶段性；重视过程评价；关注学生的学习态度。［2］作为我国教育体系中最核心、最重要的教学评价之一，高考及其评价体系对日常教学中的评价有着重要的导向作用。在2019年出台的《中国高考评价体系》中，明确提出了“一核”“四层”“四翼”的设计，如图1 所示，为具体教学过程中的评价工作指明了方向。

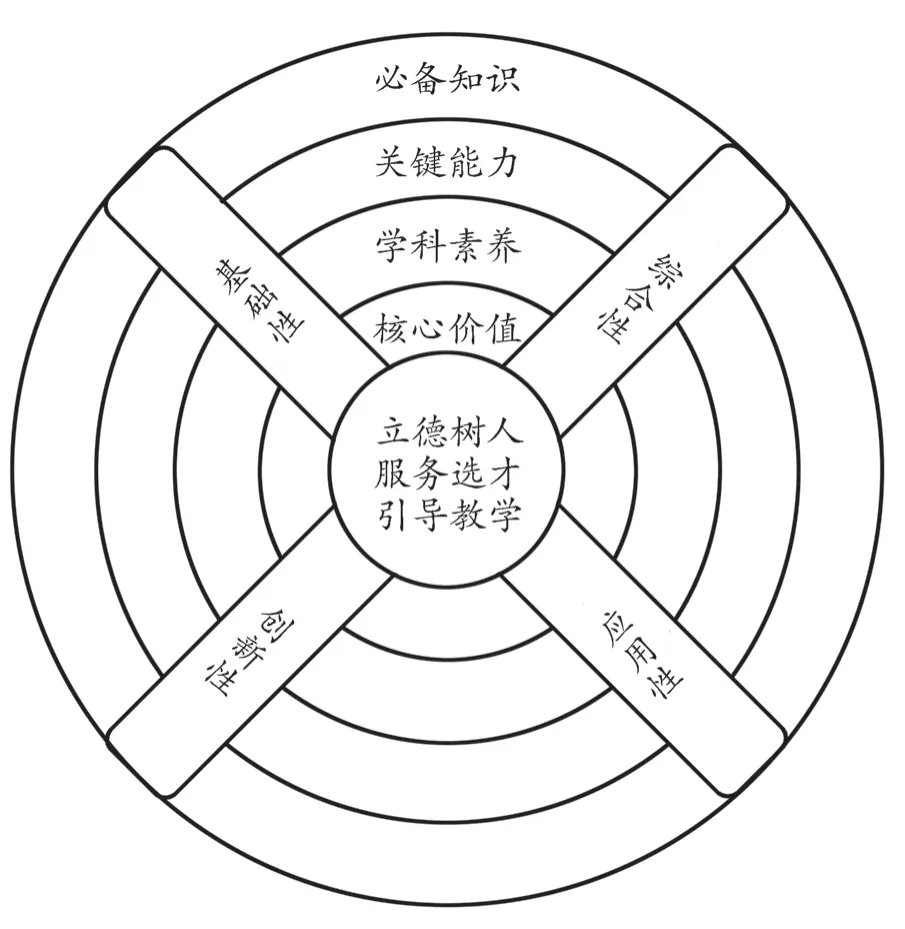
图1 《中国高考评价体系》的“一核”“四层”“四翼”［3］

一、数学建模的基本过程、素养表现与评价

根据上述思想，结合数学建模素养开放性、探究性和实践性的特点，我们认为，数学建模的评价可以在“四翼”中的综合性、应用性、创新性要求的引领下，从数学建模的各个环节入手来设计问题，以期达到考查学生数学建模素养的目的。数学建模活动的基本过程如图2所示。

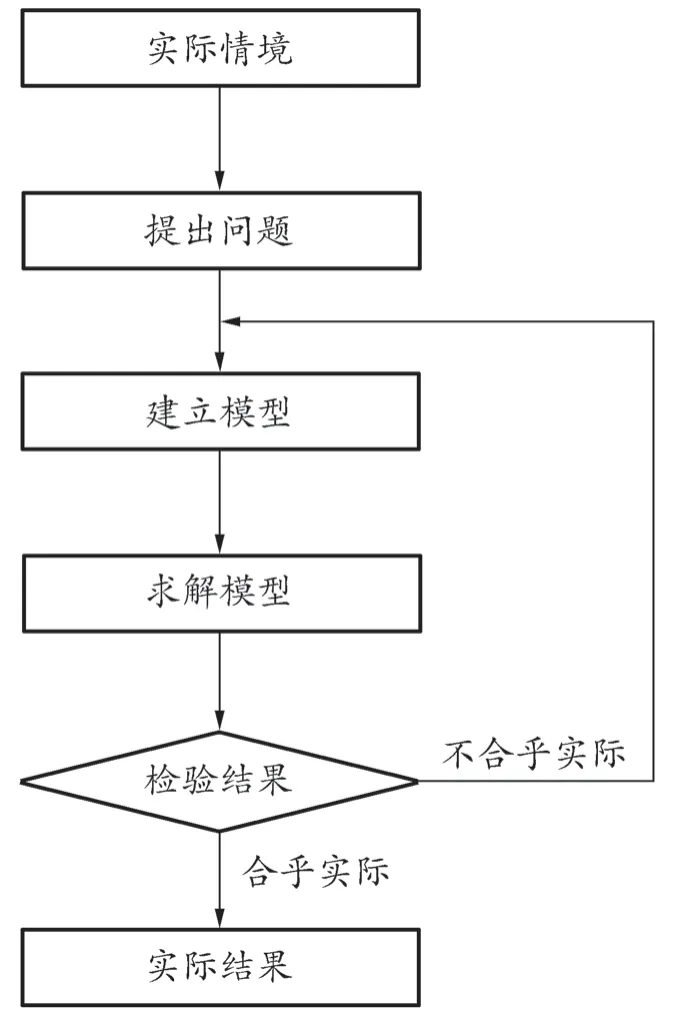
图2 数学建模活动的基本过程［2］

在数学建模的各个环节中，对这一核心素养的体现是全方位的。在从“实际情境”到“提出问题”的环节中，需要具备发现情境中的数学关系，提出数学问题的能力（情境与问题）；在“建立模型”“求解模型”环节中，需要能够创造性地建立数学模型，解决问题（知识与技能）；而在“建模—解模—检验”的循环中，需要理解数学建模的意义和作用，运用数学语言，清晰、准确地表达数学建模的过程和结果（思维与表达）；在回归“实际结果”的环节中，则需要学生通过数学建模的结论和思想阐释科学规律和社会现象（交流与反思）。《2017 版课标》也对这四个维度在数学建模素养的三个水平上的表现进行了更细致的阐述，可以归结为表1。

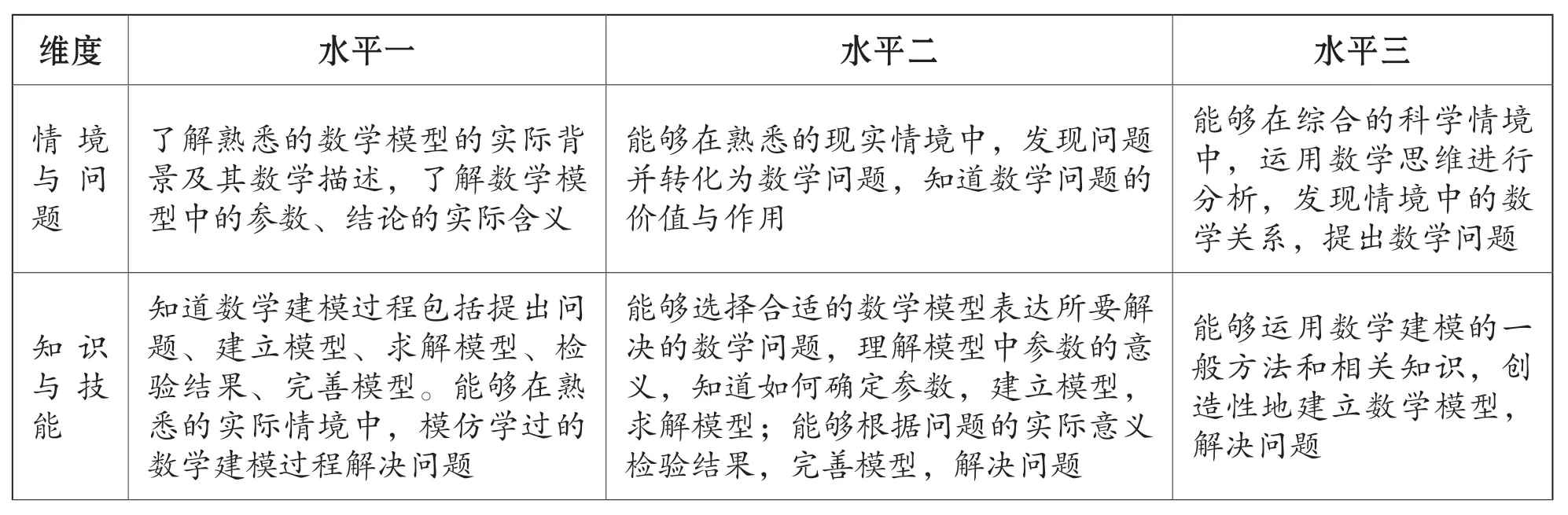
表1 数学建模素养的水平划分［4］

《2017 版课标》指出，对数学建模素养的评价应遵循上述划分标准，同时也要依据满意原则和加分原则。在《2017 版课标》中反复提及的这两个原则，落实到数学建模素养的评价时可以理解为：“满意原则”由教师灵活掌握，教师认可，即认为达到满意水平，不必追求最优解和唯一解；“加分原则”在数学建模素养的评价中则反映在方法的创新性、模型的原创性、表达的准确性等方面。［4］

二、基于数学建模六环节的案例评价设计

通过撷取数学建模六环节中的“提出问题”“建立模型”“求解模型”“检验结果”诸环节，根据高考评价体系中的综合性、创新性和应用性，笔者结合以下案例来阐述对评价选材、评价要素以及评价标准等方面的思考。

案例 某校的机器人社团为了准备参加比赛，需要为他们制作的智能小车设计一条试运行轨道。按照大赛的规则，轨道中应包含一个供小车爬坡的弯道。弯道两头的直道相对位置如图3 所示。

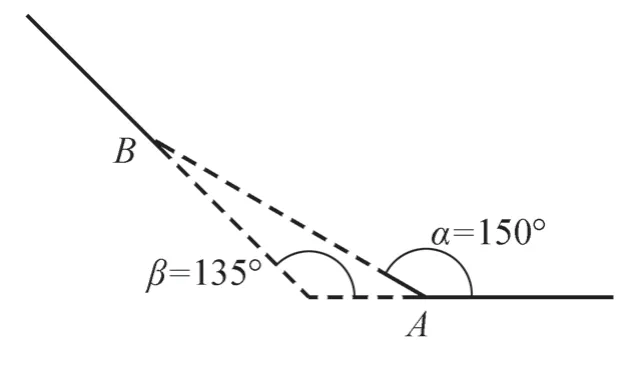
图3 弯道两头的直道相对位置

为保证小车行进顺利，A、B两点处轨道应当平滑地连接起来，即弯道与直道之间不能形成“拐角”。请根据上述要求，为机器人社团设计一个符合要求的弯道。［5］

（一）在综合情境中提出问题

在传统的数学教学中，学生习惯于扮演“解题者”的角色，通常只是被动地接受题干给出的条件，运用所学知识进行求解。而这些已知条件往往是经过命题人“裁剪”的，可谓“不多不少，繁简适中”。但是在数学建模中，情况发生了改变。由于问题往往来自实际情境，由可能获得的数据与约束构成的已知条件可能多于求解时所需的；同时，有些条件的细节过于复杂，并不适合原封不动地加入考虑因素中，需要作适当的理想化处理以便获得实用的模型。

在评价选材时，要注意所谓综合情境应当是直接来自实际生活、科学现象等，未经数学化的问题。在评价过程中，需要关注的数学建模过程要素是提出问题的环节，也就是选择问题中的主要因素，建立它们之间的数学关系，把问题数学化，并准确地表述出来。而评价标准则应当在参照表1 的同时掌握满意原则和加分原则。在提出问题的环节中，满意原则可表现为：即使学生简化问题的方式与教师的预设不一致，只要合理，也可以认定已经达到相应的素养水平；而加分原则表现为：如果学生能够考虑较复杂的简化方式，甚至引用非数学领域的知识，提出更贴近原始情境的问题，则可以认定已经达到了更高的素养水平。

环节1——提出问题

（1）评价选材：近年来，随着3D 打印、激光雕刻等技术的普及，相关的图形设计问题也逐步走进了中学生的学习生活中。本例提示学生可以结合导数的知识，建立函数模型来解决相关的设计问题。

（2）评价要素：重点考查学生将复杂的实际情境与熟悉的函数模型进行联系，进而将直观认知的问题数学化的能力。

（3）评价标准：对学生所提问题的评价可以分为两个层面。若学生能简化情境，并尝试将熟悉的函数图像作为模型的备选方案，则可以认为给出了满意答案；若学生能适当引入跨学科知识（如运动学），帮助分析并提出更贴近真实情境的问题，则可以适当加分。

（4）解答梗概：以点A为原点，水平向右的方向为x轴正方向建立平面直角坐标系，不妨设点B的坐标为。求函数， 使得且。学生可能提出的问题及相关的参考评价依据如表2 所示［2］。

表2 学生回答与评价示例

（5）案例亮点：从表2 的第二个示例回答可以看到，结合运动学的知识，可将要求中的“平滑”解读为曲线在衔接处的切线方向与直道一致，从而通过导数知识转化为对函数的限制条件，体现了“四翼”中的综合性［3］。

（二）在建模解模中寻求创新

数学建模评价设计的一大难点在于素材的选择。不少教师都有这样的体验：设计评价时选择的问题往往要么偏向真实情境，条件太复杂，以至于不适合作为评价材料；要么偏向传统习题，接近应用题，以至于无法考查数学建模素养。其实很多传统应用题是经由实际情形简化而来，因此将这些应用题进行逆向改造，可以成为好的评价材料。改造的手段包括但不限于：将数学语言表述的条件还原为自然语言表述，增加变量个数，将变量之间明确的等量关系改为不确定的不等关系，等等。

在对建模解模的评价过程中，评价的要素主要体现在选择参数，建立参数之间的数学关系，运用相关数学知识求解等方面。而在评价标准上，如果建模合理，解模正确，就可以认定已达到满意原则的要求；而建立优化的模型，运用有创造性的方式求解，则可根据加分原则予以加分。总的来说，如何让传统素材在数学建模的评价中发挥新作用是值得关注的。

环节2——建立模型、求解模型

（1）评价选材：本例的建模与求解环节脱胎于经典的“待定系数法”，但边界条件的复杂性导致了函数模型选择与求解过程的开放性。

（2）评价要素：重点考查学生从已知函数模型中甄选适当对象的能力，同时对学生提出了创新能力方面的挑战，要求跳出固有的思维模式来求解问题。

（3）评价标准：对学生建模解模的评价可以分为两个方面。

在建模过程中，若学生经尝试后能排除抛物线、圆弧等模型，转而考虑有可能同时满足两组边界条件的函数模型，则根据满意原则认为在建立模型的环节达到了数学建模素养水平二的要求；若学生能基于对函数性质的认识，识别出一些简单而适用的模型（如三次函数、三角函数等），则根据加分原则，可以加分。

在解模过程中，若学生能运用信息技术等手段，求出数值解，则根据满意原则认为在求解模型的环节达到了数学建模素养水平二的要求；若学生能够使用目标函数的性质求出精确解，则根据加分原则，可以加分。

（4）解答梗概：可以选择三次函数模型或三角函数模型进行求解。可能的解决方案包括但不限于，等。

（5）案例亮点：本例对函数模型的选择和求解拓展了学生对“待定系数法”的认识。这种将传统中学数学思想方法加以创造性使用的做法符合“四翼”中的创新性所强调的：发现新问题、找到新规律、得出新结论［3］。

（三）在结果检验中突出应用

数学建模素养除了在“情境与问题”维度有较高要求之外，在“交流与反思”维度也有独到之处，特别是提出了对模型及其运算结果进行评价的要求。《2017 版课标》中将数学建模素养在交流与反思维度的表现划分为以下三个层次：能够借助或引用已有数学建模的结果说明问题；能够用模型的思想说明问题；能够通过数学建模的结论和思想阐释科学规律和社会现象。［2］

在评价时主要关注学生运用数学建模结果与思想，建立数学运算的过程、结论与原始问题之间的联系并加以表达的能力。由于评价的对象是学生对模型的评价，因此只要评价是合理的，条理是清晰的，就可以认为是满意答案。而当学生能够从数学建模的思想出发给出具有独创性的评价，或者在模型与问题之间建立更深层次的联系时，可以加分。

环节3——检验结果

（1）评价选材：本例的评价关注不同函数模型之间的比较，需要对不同模型进行定量的比较来评判其优势与不足。

（2）评价要素：关注“检验结果”的环节，重点考查学生运用已有数学建模的结果和评价标准对数学建模的过程与结果进行评价的能力，以及在此基础上发展出新的评价标准的能力。

（4）解答梗概：可以使用模型在A、B两点处的曲率、来对二者进行比较。以三次函数和三角函数的模型为例，相关比较结果如表3 所示。

表3 两种模型的曲率对比

因此在A、B两点处，都是三角函数模型的设计更加平滑。

（5）案例亮点：本例选取的素材贴近时代、贴近社会、贴近生活，与“四翼”中的应用性要求高度吻合。同时，对学生回答的评价方式也可以体现与应用性相符的“结论开放、解题方法多样、答案不唯一”特点［3］，从小处体现了打破“五唯论”的价值导向。

三、结语

在上面案例中，我们的讨论涉及数学建模的不同环节，并按照满意原则与加分原则分别进行评价。其中包含了丰富的数学建模素养要素以及“满意原则”“加分原则”这两条评价原则的具体表现。

综上所述，数学建模的评价中需要关注的内容是多方面的，可以归纳为着重考查数学建模对学生数学素养提升的作用，特别是在“三会”方面的表现。例如，发展学生对实际情境进行适当简化并提出相应数学问题的能力，可以引导学生用数学眼光观察世界；而数学建模素养的培养，不仅仅局限于传统的“应用题”模式，也在其他问题形式中得到体现，可以启发学生用数学思维思考世界；此外，对模型进行解释，则是数学建模与数学表达之间的联动，可以增强学生用数学语言表达世界的能力。

因此，我们对数学建模的评价所作的思考可以归纳为如下建议：要依据数学建模的各个环节来设计评价内容；评价过程中要重视建模思想与经典知识的互动；要遵循满意原则和加分原则去评价。