时间窗约束下的无人集群分布式任务分配算法

李瑞琳，崔 巍，冯彦翔，杨宜康

(西安交通大学自动化科学与工程学院，陕西 西安 710049)

0 引言

由于具有灵活性强、装配便捷、成本消耗低等优势[1],无人机已广泛应用在搜救、交通巡查、遥感测绘等领域[2]。单架无人机经常无法保证任务的高效执行,因此需要多架无人机组成无人集群联合或协同执行任务。无人集群协同任务分配是指综合考虑任务特点、平台性能和任务环境,以优化目标为牵引,将任务分配给多架无人机,使得整个系统执行任务消耗的成本最低或效率最高[3]。近年来,无人集群任务分配问题已成为无人集群协同规划领域亟需解决的关键问题[4]。

无人集群任务分配模型一般分为单一任务模型和多任务模型。单一任务模型包括多旅行商问题模型[5]、车辆路径问题模型[6]等;多任务模型有网络流模型和混合整数线性规划模型[7]等。单任务模型中各个任务间的模型空间相互独立,而多任务模型中多个任务间的模型空间是共享的,但在实际场景下,可能产生跷跷板现象,即部分任务效果提升,但另一部分任务效果下降。

无人集群任务分配方法分为集中式和分布式两种思路。集中式任务分配算法中由中央处理单元整合全局信息做出决策[8],常见的集中式方法有最优化方法[8-9]和元启发式算法[10-17]。其中,文献[14]提出一种遗传-蚁群混合算法并对侦察任务分配问题进行求解;文献[15]提出了基于粒子收敛程度的自适应惯性权重与量子门变异算子,改造了标准量粒子群算法;文献[16]引入二进制矩阵与自适应惯性因子对侦察任务进行分配求解。集中式方法结构简单,但速度较慢,鲁棒性差。

分布式任务分配方法通过各无人机之间的交流、协商、决策,协同分配任务,因此分布式方法灵活性强,对单点故障具有一定鲁棒性,能降低安全风险和成本。分布式方法有拍卖算法[18-20]、合同网算法及其相应的改进算法(extend contract net protocol, ECNP)等[21-23]。其中,文献[19]提出一致性联盟包算法(consensus-based bundle algorithm, CBBA),采用基于市场的决策策略作为分配任务选择机制,并使用基于局部通信的共识作为冲突消解机制;文献[22]对CBBA算法进行了改进,考虑了异步通信、时间敏感和动态的任务、任务空间中的障碍和干扰等问题。文献[24]提出性能影响算法(performance impact algorithm, PI)来解决无人集群任务分配问题,优化利益问题的总体目标。相比于CBBA算法中每个无人机致力于降低其局部成本,PI算法旨在优化整个系统的总体成本。

同集中式方法相比,分布式任务分配算法依赖智能体之间的交流通信质量,很少考虑真实环境中的一些要素。例如,文献[25]考虑了无人机飞行能力、任务执行时间窗等约束条件,但忽略了任务执行时间长度的约束;文献[26]提出了一种“闭环CBBA”,考虑任务完成后无人机返回起飞基地,但忽略了任务分配过程中的各项约束;文献[27]基于CBBA框架提出了CBBATW算法,对任务有效时间窗、车辆燃油成本进行了适当的处理,但在任务时间窗约束较严格时,容易出现任务无法完全分配问题;文献[28]对PI算法引入动态重调度模块和Softmax函数以应对环境的动态变化,但没有考虑到任务的时间窗约束等条件。

针对上述问题,文中基于分布式PI算法框架,考虑具有时间窗约束的无人集群协同任务分配问题,提出一种以任务平均完成时间最小为优化目标的分布式任务分配算法(distributed allocation with time windows,DATW)。文中的时间窗约束属于“硬约束”,即任务必须在时间窗内被执行,否则不予分配。整个算法在所有无人机上并行运行,通过反复执行任务添加、冲突消解和任务再分配三个阶段,得到满足时间窗约束的任务分配结果。最后进行不同规模的仿真实验,验证所提算法的可行性和实用性。研究的主要创新点为:

1) 将任务的时间窗约束嵌入到PI分布式算法架构中,使得被分配的任务均满足时间窗约束。

2) 同传统PI算法相比,针对因不满足时间窗约束而无法分配的任务,提出新的第三个阶段:以无人机局部时间成本最小为优化目标的任务再分配策略。由此任务再分配阶段提高了13.76%的任务分配成功率。

3) 与CBBATW算法[27]相比,提出的DATW算法的任务分配成功率平均值提高了21.94%,任务平均完成时间降低了24.25 s,所以性能更好。

4) 相比于ECNP算法[23],DATW算法不受无人机通信拓扑变化的影响,在各种拓扑下都能进行充分交流,适应性更强。

1 问题描述

本研究考虑时间窗约束的无人集群协同任务分配问题。给定m个任务Nt={t1,t2, …,tm}和n架无人机Nu={u1,u2, …,un},且n>m。任务tj∈Nt由二元组表示,其中loc(tj)=(xj,yj,zj)是tj三维坐标,Dj是执行任务tj所需时间;无人机ui∈Nu由表示,loc(ui)=(xi,yi,zi)是ui的初始位置坐标,vi表示飞行速度。无人机的动态情况改变会影响其飞行性能。因此,为了简化计算,假设无人机ui的速度vi为一个常数。无人机之间通过局部链路进行通信,相应的通信拓扑网络可用n×n维的对称邻接矩阵G表示,其元素Gih=1表示无人机ui和uh互为邻近无人机,彼此可以交换共享信息;Gih=0表示ui和uh不能通信。

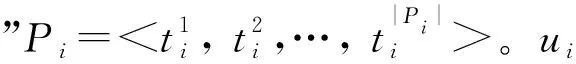
在实际情况下,无人集群任务分配结果会受到来自于无人机和任务两个方面因素的影响。

1) 无人机因素

由于不同无人机具有不同速度,其执行任务的时间成本也不同。令tj∈Pi,无人机ui开始执行任务tj的时间Tj(Pi)可表示为:

(1)

式中:tk表示路径Pi中tj的前一个任务;dis(·)表示两个坐标之间的欧几里得距离。

无人机ui完成任务tj所需的“时间成本”Fj(Pi)可表示为:

Fj(Pi)=Tj(Pi)+Dj

(2)

无人机执行任务能力受限影响可表示为[24]:

|Pi|≤Li,∀ui∈Nu

(3)

式中:|Pi|表示Pi中的任务数;Li表示无人机ui的执行任务数上限。

2) 任务因素

任务的开始执行时间必须满足时间窗“硬”约束。令任务tj必须不早于时间Tj_start执行,不晚于时间Tj_end执行,即:

Tj(Pi)∈[Tj_start,Tj_end]

(4)

在任务分配问题中,最小化原则可以分为MiniSum和MiniMax。MiniSum准则一般用于最小化所有无人机的资源总消耗或完成每个任务的平均成本,而MiniMax则是最小化成本最高的无人机的成本。对于无等待分配问题,由于任务时间窗约束的存在,意味着一个无人机的任务分配情况会改变另一个无人机的可用选择,每个无人机的时间成本会受到其他无人机的影响。此时,MiniMax准则难以反映不同无人机之间的关系,而MiniSum准则可以在无等待任务分配上获得更好的效果,因此文中选择MiniSum准则。

在满足上述无人机和任务约束的前提下,以任务的平均时间成本为优化目标,研究无人集群协同任务分配问题,相应的数学模型为:

(5)

s.t.Pi∩Pj=∅,∀i≠j

(6)

|Pi|≤Li,∀ui∈Nu

(7)

Tj_start≤Tj(Pi)≤Tj_end,∀tj∈Pi,∀ui∈Nu

(8)

其中,式(5)为目标函数,表示任务的平均时间成本最小;式(6)规定每个任务只能指派给一个无人机,且不能重复分配[24];式(7)规定无人机ui一次执行任务数不能超过Li;式(8)引入了一个非凸约束,规定任务的开始执行时间满足时间窗约束。全局优化目标是非凸的,它由无人机的任务列表、任务坐标和每个无人机的飞行速度共同决定。因此所研究的多无人机任务分配问题是NP-hard问题[29-30],无法通过简单计算直接获得全局最优解。

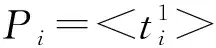
2 无人集群分布式任务分配算法

文中提出一种考虑时间窗约束的分布式任务分配算法(DATW)。所提出的DATW算法在所有无人机上并行运行。无人机之间通过局部通信拓扑交换信息,记录所有任务的分配结果和任务增益等信息。算法主要包括任务添加、冲突消解和任务再分配三个阶段。算法先循环迭代执行前两个阶段,当所有无人机记录的任务分配对象列表一致且在一段时间内不发改变时,开始执行第三个阶段,继续将一些未分配的任务分给无人机。经过多轮迭代后,最终得到任务平均时间成本最小且满足时间窗约束的无冲突任务分配结果。

首先,定义无人机ui记录的信息列表。

1) 任务分配对象列表

Zi=[Zi1,Zi2, … ,Zim]T表示无人机ui记录的所有任务的分配对象,分量Zij=k表示ui认为任务tj被分配给了uk。如果ui认为tj未分配,则Zij趋近无穷大,即Zij→∞。

2) 任务增益列表

Qi=[Qi1,Qi2, … ,Qim]T表示无人机ui记录的所有任务的增益。当Zij=k时,Qij等于将任务tj从Pk中删除后,uk的时间成本的减少量。注意,如果Zij→∞,则令Qij→∞。

3) 任务开始执行时间列表

Ti=[Ti1,Ti2, … ,Tim]T表示无人机ui记录的所有任务的开始执行时间。当Zij=k时,Tij反映uk开始执行任务tj的时间。如果Zij→∞,则令Tij→∞。

4) 时间戳列表

si=[si1,si2, … ,sin]T记录无人机ui从无人机uh获得最新信息的时刻,分量sih可表示为[19]:

(9)

式中τr表示ui接收uh信息的时刻。

初始时,令Pi=∅,Zij→∞,Qij→∞,∀tj。无人机ui与邻近无人机在通信中互换上述四种信息。

2.1 任务添加阶段

1) 任务增益

假设任务tj位于Pi中,令Pi⊖tj表示将tj从Pi中移除后剩余的任务序列,增益qij(Pi⊖tj)表示将tj从Pi删除后无人机ui时间成本的变化量,按式(10)计算[24]:

(10)

增益qij(Pi⊖tj)反应了tj对于ui当前时间成本的“贡献值”。当tj∉Pi时,令qij(Pi⊖tj)→∞。

2) 任务边际增益

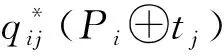
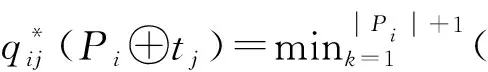
(11)

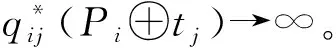
在任务添加阶段给无人机ui分配任务时,只有当任务tj同时满足下面两个条件,它才会被允许插入到Pi中。

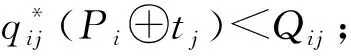
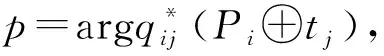
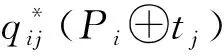
(12)

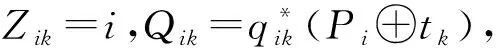
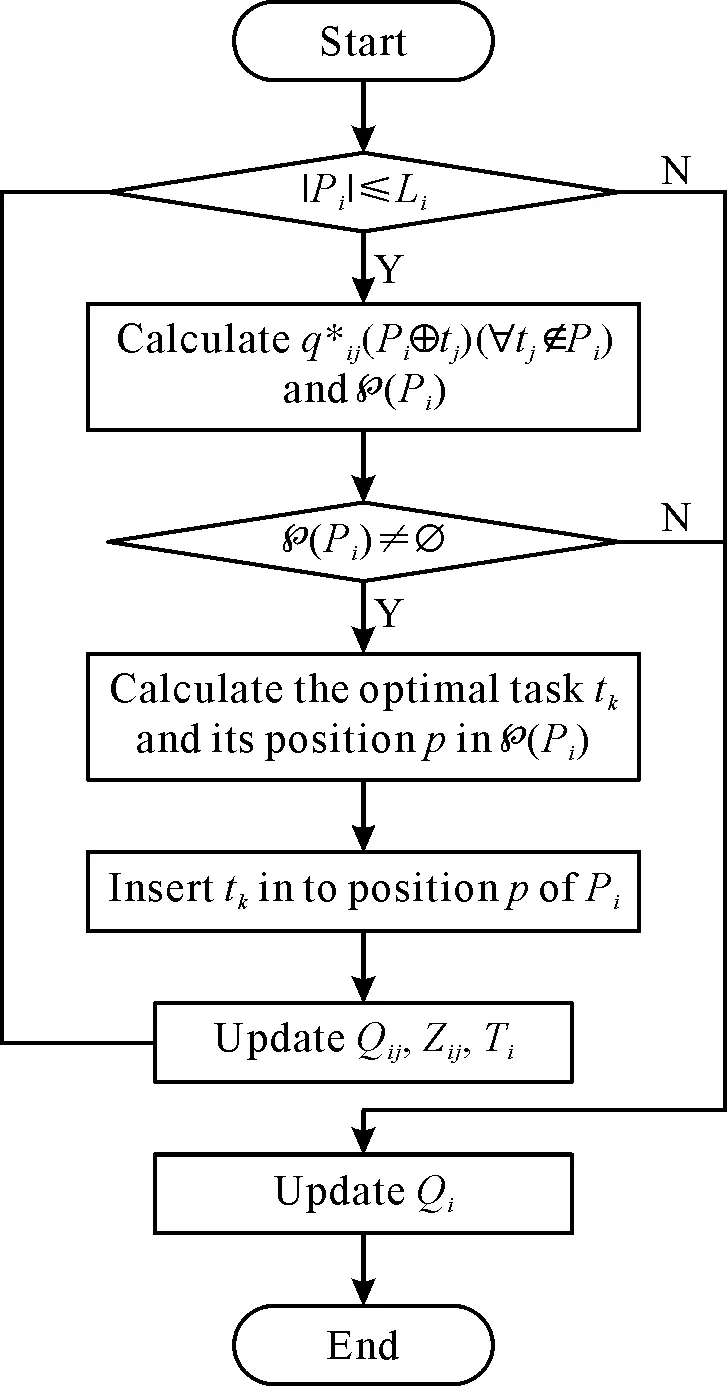
图1 ui执行的任务添加过程Fig.1 The process of adding tasks performed by ui

2.2 冲突消解阶段

若算法在所有无人机上并行执行,同一项任务可能会同时分配给多个无人机,产生分配冲突。因此,为获得无冲突的任务分配结果,还需执行冲突消解过程。在这个阶段无人机反复迭代执行协商一致和任务删除两步骤,直到消除了所有冲突并且所有无人机的任务分配信息保持一致,达成全局共识,即Qi=Qh,∀ui∈Nu,uh∈Nu且ui≠uh。

2.2.1 协商一致步骤

假设Gih=1,无人机ui与邻近无人机uh通过局部通信拓扑进行信息交换,共享Zi和Zh、Qi和Qh、Ti和Th、si和sh,并按照一定的交流规则更新相应信息。实际上,当无人机ui收到邻近uh发来的信息后,会根据Zi和si来判断接收到的信息是否为任务tj的最新信息,并以降低自身时间成本为目标,按照表1所示的交流规则决定是否更新自身存储的信息Zi,Qi和Ti。表1共包含以下三种操作:

表1 无人机交流规则Table 1 UAV communication rule

1) 更新(update):Zij=Zhj,Qij=Qhj,Tij=Thj;

2) 保留(leave):不执行任何操作;

3) 重置(reset):Zij→∞,Qij→∞,Tij→∞。

其中,默认操作为保留。此外,储存在无人机ui上的时间戳si表示获得信息的最新时间,因此ui每次接收信息后都需要按照式(9)更新si。

2.2.2 任务删除步骤

利用局部通信网进行协商一致步骤后,无人机ui检查当前任务路径Pi,从中删除集合A={tj∈Pi|Zij≠i}和集合B={tj∈Pi|Tj(Pi)Tj_end}中的任务。其中,A表示Zi和Pi不匹配的任务集合,B表示不符合时间窗约束的任务集合。

首先,无人机ui根据式(13),将能够最大程度减小执行时间成本的任务tk从Pi和A中同时移除。重复此过程,直到A中的所有任务都不再满足(13)或A为空。

(13)

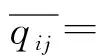
若上述过程结束后A≠∅,将A中任务的执行者重置为ui,即对于所有剩余任务tj∈A,令Zij=i。

然后,无人机ui检查自身序列Pi,一旦存在任务tj∈Pi不满足时间窗约束,则将tj从序列Pi中移除,并重置信息列表Zij→∞,Qij→∞,Tij→∞。无人机ui每移除一个任务tj,都需要重新计算Pi中各任务的开始执行时间,判断是否出现不符合时间窗约束的新任务。重复迭代执行这个过程,直至Pi上的所有任务满足时间窗约束。当任务删除操作结束后,重新计算Pi中每个任务tj的增益Qij和任务开始时间Tij。

无人机ui重复执行上述协商一致和任务删除两个步骤,当多轮迭代后任务分配结果不再发生改变,表明已实现无冲突任务分配且满足时间窗约束,完成了冲突消解阶段。可以由图2来描述这个阶段。

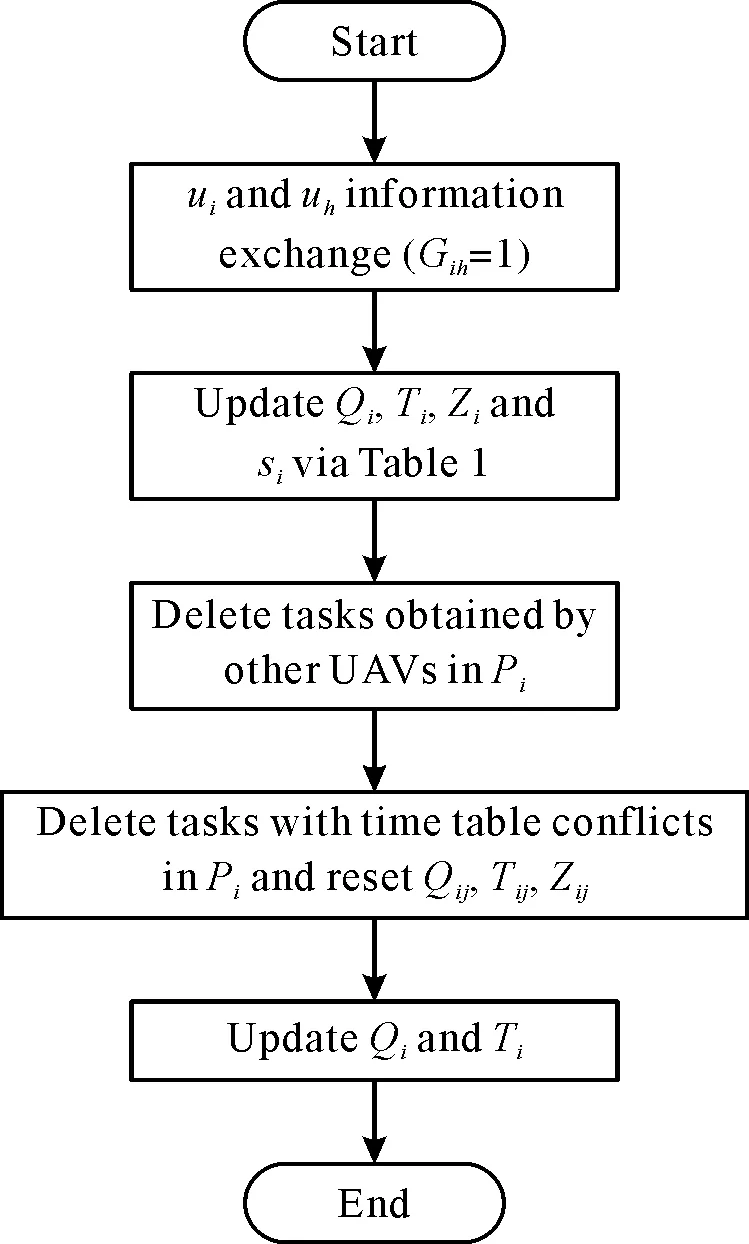
图2 ui执行的冲突消解阶段Fig.2 Conflict resolution phase of ui

2.3 任务再分配阶段

一般情况下,执行前两个阶段后得到的任务分配结果能够涵盖所有任务,但在时间窗约束较苛刻的情况下,可能有一些任务没有被分配。令C表示前两个阶段后未分配的任务集合。为了使更多的任务在满足时间窗约束的条件下被分配,还需对C中的任务执行第三个阶段——任务再分配。再分配阶段包含任务添加和冲突消解两步骤,只将C中的任务从无人机上移除或添加,对C之外已经分配的任务不再进行操作。

2.3.1 任务添加步骤

为了避免出现任务被同一个无人机重复添加再删除的操作,对无人机ui定义一个向量Mi。初始时令Mi[tj]=0,∀tj∈C。若tj被ui添加到Pi,但因违反时间窗约束而又从Pi移出后,令Mi[tj]=1。

任务tj∈C只有满足下述条件3和条件4才会被允许插入无人机ui的路径Pi中的合适位置。

条件3:Zij≠i,Mi[tj]=0;

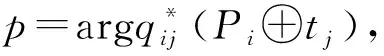
(14)

不同于式(12),本轮任务添加仅考虑了任务对于无人机的边际增益,将式(14)中的任务tk添加到Pi后,无人机ui的局部时间成本增加量最小。重复上述任务添加过程,直至式(14)不再满足或者ui执行的任务数已达最大承载量。

2.3.2 冲突消解步骤

任务再分配冲突消解也分为协商一致和任务删除两部分。

1) 协商一致

因为是针对C中任务的再分配过程,所以在此交流过程中,无人机只交换与C中任务相关的信息。协商一致的规则如表1,具体执行操作同2.2.1节中的更新、保留和重置操作。

2) 任务删除

无人机ui需要删除A′={tj∈Pi|Zij≠i}和B′={tj∈Pi|Tj(Pi)Tj_end}中的任务。其中,ui移除A′中任务的方法与2.2.2节相同。而对于任务tj∈B′,将任务tj从序列Pi中移除时,执行操作:Zij→∞,Qij→∞,Tij→∞,Mi[tj]=1。Mi[tj]设置为1是为了保证在当前任务再分配阶段中,tj将不会再被添加进Pi,从而避免无效的任务添加和移除,提高任务分配效率。无人机ui每移除一个任务tj,都需要重新计算Pi中任务的开始执行时间,判断是否出现不符合时间窗约束的新任务。

无人机ui重复迭代地移除B′中任务,直至B′=∅,即Pi中的所有任务满足时间窗约束。任务删除过程结束后,计算Qij和Tij,∀tj∈Pi。

2.4 收敛性分析

文中所提出的DATW算法包括任务初分配和任务再分配两部分。其中,任务初分配过程对应于2.1节和2.2节描述的任务添加和冲突消解两个阶段。初分配结果可能不会覆盖全部任务,因此需要执行2.3节中的任务再分配阶段,尽可能的提高任务分配成功率。

DATW算法基于迭代优化原理展开,每一架无人机在每轮迭代中的目标是降低全局时间成本,并尽可能把所有任务分配给无人机。具体来讲,每架无人机计算执行自身任务路径的时间成本,并与其他无人机视角下对应任务的执行成本相比较,递归地选择从自身任务路径中保留或移除任务,以此来降低全局时间成本。同时,通过第三个任务再分配阶段,尽可能地分配任务。最终实现最小化任务平均完成时间的总目标。

任务分配过程中,每架无人机的任务增益列表不断更新,反映了当前的分配情况。当所有无人机的任务分配信息保持一致,达成全局共识,即Qi=Qh,∀ui∈Nu,uh∈Nu且ui≠uh时,算法收敛。

DATW算法在所有无人机上并行执行,流程图如图3所示。

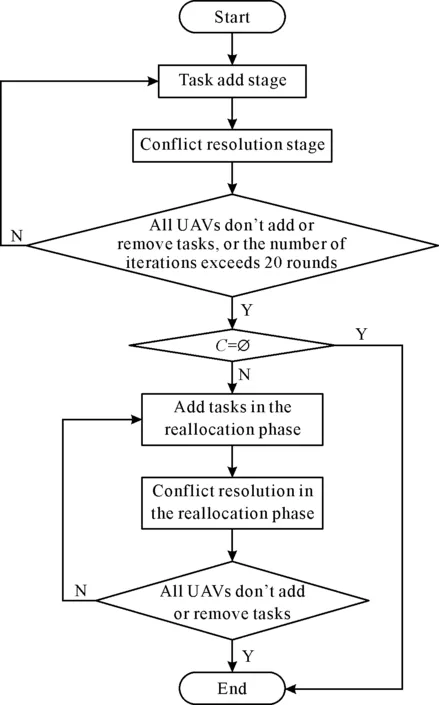
图3 DATW算法流程图Fig.3 Flow chart of DATW algorithm

DATW算法具体步骤可总结如下:

Step 1 根据2.1节执行任务添加阶段。

Step 2 根据2.2节循环执行冲突消解阶段,直到所有无人机的增益列表不发生改变。

Step 3 循环执行Step 1和Step 2,直到所有无人机不添加或移除任务,或迭代次数超过20轮。计算未分配任务集合C,若C=∅,算法结束。

Step 4 对C中的任务执行再分配阶段任务添加。

Step 5 执行再分配阶段冲突消解,循环执行再分配协商一致阶段和再分配任务删除阶段,直到所有无人机的增益列表不发生改变。

Step 6 循环Step 4和Step 5,直到所有无人机不添加或移除任务,算法结束。

3 算法仿真分析

假设任务分布在10 000 m×10 000 m×1 000 m的三维区域,无人机初始时分布在10 000 m× 10 000 m二维平面,无人机的飞行速度恒为50 m/s,每架无人机最多执行任务数为5,任务时间窗口的最晚完成时间不大于500 s,任务的执行时间均为30 s。针对无人机数为n和任务数为m的算例,随机生成所有无人机和任务的坐标和每个任务对应的时间窗约束条件。注意当时间窗约束较为严格时,可能存在无法分配的任务。

文中进行了两组实验:第一组验证在不同规模算例中DATW算法的任务再分配阶段的有效性;第二组验证不同通信拓扑环境下DATW算法的适用性,检验算法能否成功分配所有任务,分析所有任务都分配后的任务的平均完成时间。第二组实验同时与CBBATW[27]算法和ECNP[23]算法进行了对比分析,为了能够与DATW算法进行对比,对CBBATW和ECNP依据实验场景进行了必要的调整。

为更方便评估任务分配解的质量,首先规定任务分配成功率为μ=M/m,其中M为分配给集群系统的任务个数。在实验1中只对比分析解的成功率μ,在实验2中先比较任务完全分配的概率,再分析对比μ=100%的场景中所有任务的平均完成时间。

实验1 在通信拓扑为全联通情况下(如图4(a)所示),考虑6种规模的无人集群任务分配问题n×m∈{(3, 7), (6, 12), (9, 20), (12, 25), (15, 30), (30, 70)}。令DATW_1表示不具备任务再分配阶段的DATW算法。对于每种算例,随机生成10个场景,在每个场景上分别运行DATW_1和DATW算法,统计每种算例中μ的最大值、平均值和最小值。实验结果如表2所示。通过仿真可知,在所有算例中,DATW算法取得比DATW_1算法更好的任务分配成功率,平均提高了13.76%的任务成功分配率。这表明了文中所提出的任务再分配阶段是有效的且高效的,在满足时间窗约束的前提下,能尽可能把任务分配给无人集群系统。

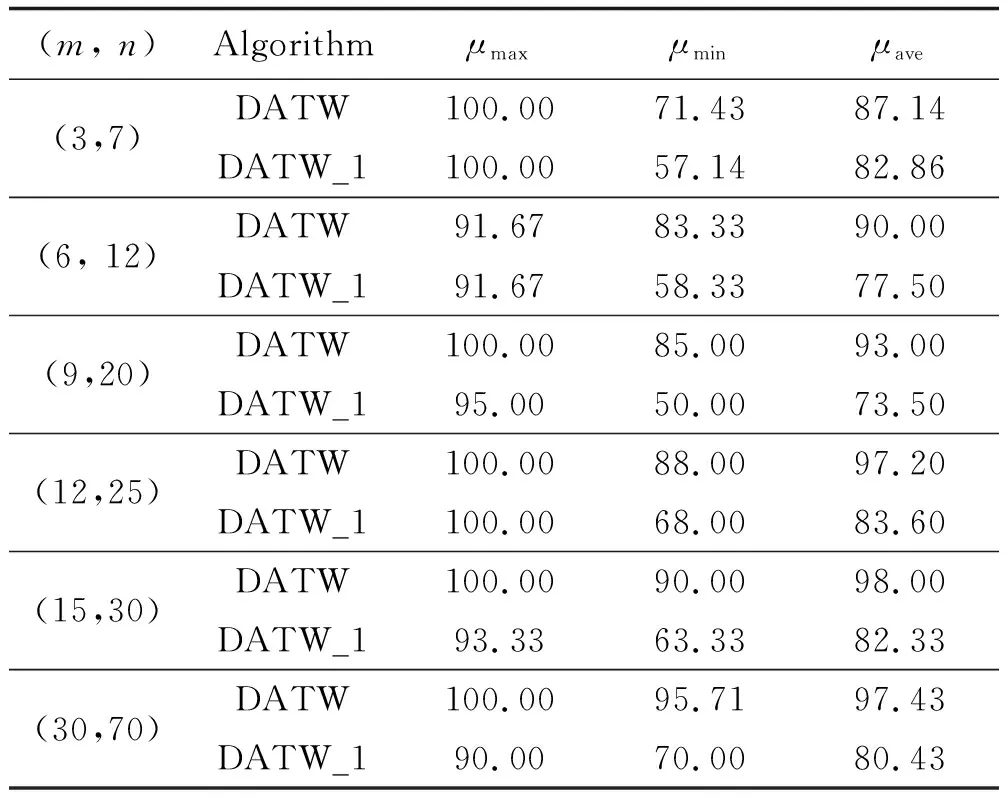
表2 DATW算法有效性验证Table 2 Validation of DATW algorithm %

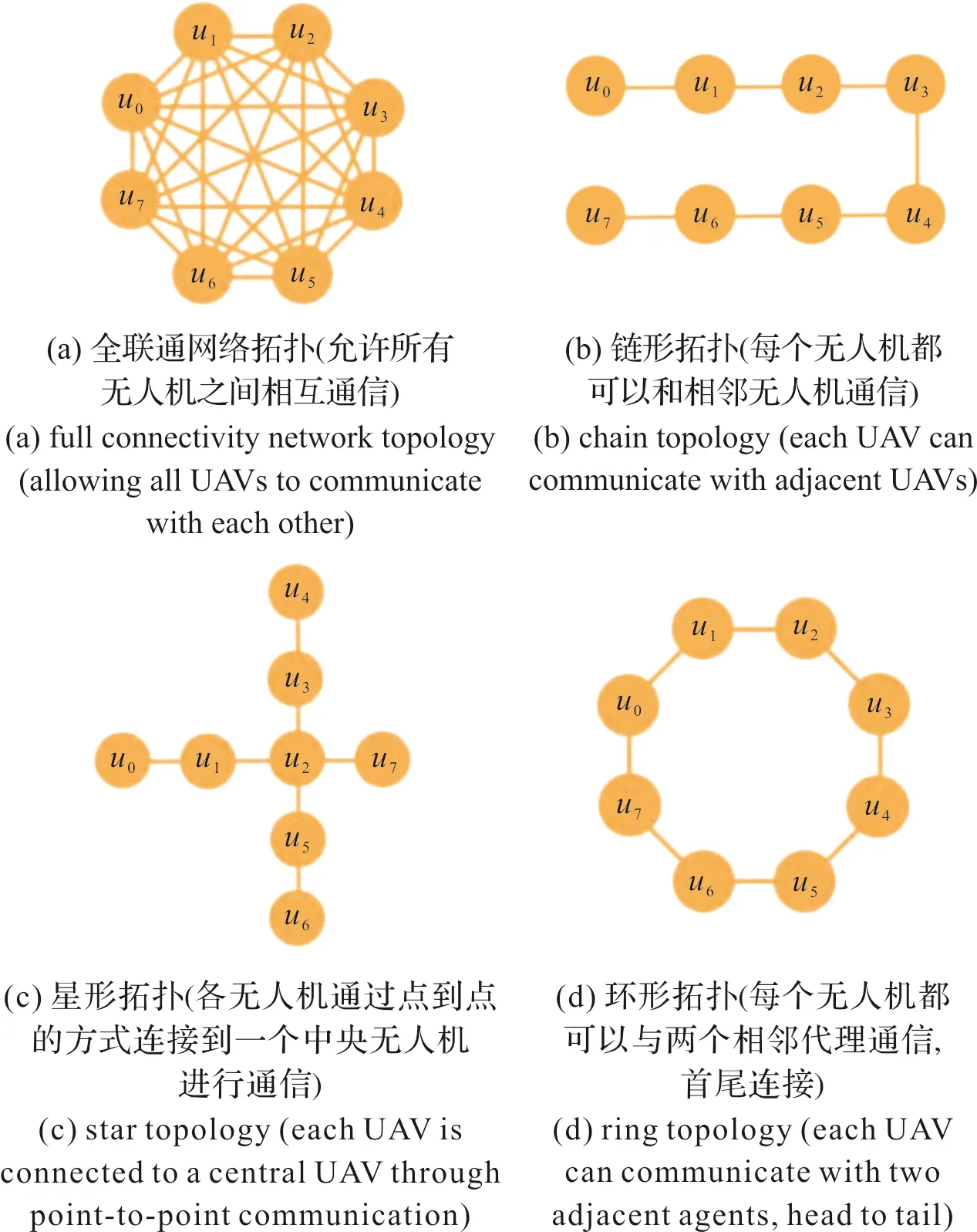
图4 四种通信拓扑Fig.4 Four communication topologies

实验2 无人集群内部的通信拓扑关系会对信息交流产生较大影响。诸如全联通网(见图4(a))的密集通信拓扑能促进集群无人机之间的信息交流,而实际上受限于通信链路约束,无人集群系统之间往往以稀疏通信拓扑为主(如链形、星形、环形拓扑,见图4(b)～图4(d)。

为了全面验证文中提出的DATW算法在不同通信拓扑下的性能和适应性,本实验分别考虑3种规模的算例,即n×m∈{(6, 12), (12, 25), (30, 70)}。每种规模下随机生成场景数为30,在每个场景上基于上述四种拓扑分别运行DATW算法、CBBATW算法和ECNP算法,分别统计μ=100%的概率。同时,统计当μ=100%时,任务的平均完成时间的最大值、最小值和平均值,实验结果如表3所示。通过仿真可以得出:1)在全联通拓扑下,ECNP算法性能表现最好,DATW算法稍差一点,但远比CBBATW算法表现好,CBBATW算法在(30, 70)的算例中任务完全分配概率仅为33.33%,相应的任务平均完成时间也明显高于DATW和ECNP算法;2) ECNP算法在链形、星形、环形拓扑下,任务完全分配率大幅下降,任务平均完成时间增大,性能变差,这说明ECNP算法依赖于通信拓扑。但DATW和CBBATW在链形、星形、环形拓扑下的实验结果和全联通拓扑下的结果相近,这表明DATW和CBBATW算法受拓扑关系影响较小,适应性更强;3) CBBATW算法随实验规模增大,性能大幅降低,成功分配所有任务的概率最低,在所有算例μ=100%的场景中的任务平均完成时间均值最低,与CBBATW算法相比,DATW算法的任务完全分配率平均提升了21.94%,平均完成时间提升了24.25 s。因此,DATW算法能尽可能地成功分配所有的任务,且得到的解质量更好。

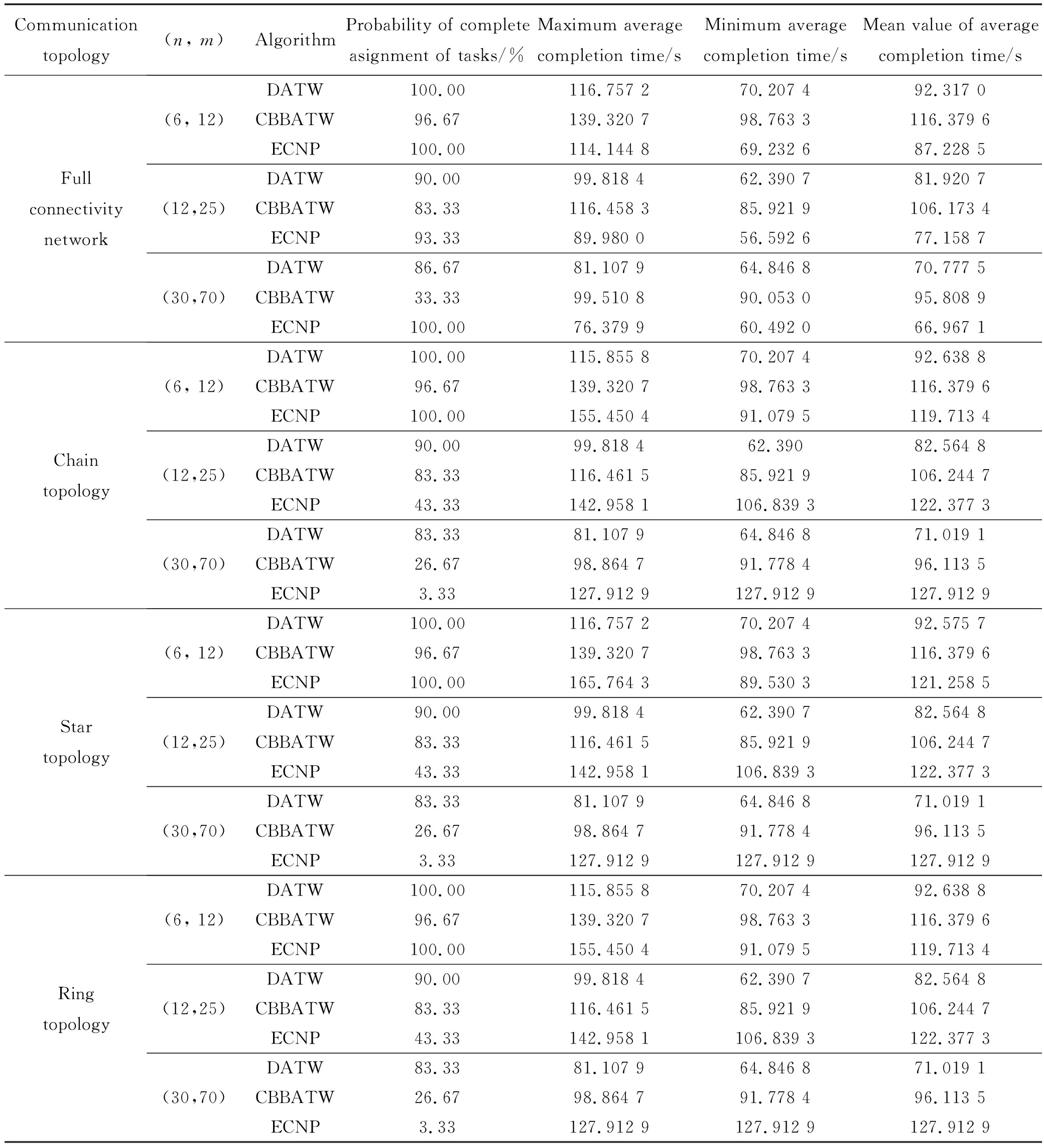
表3 四种拓扑下三种算法性能表现Table 3 Performance of three algorithms under four topologies

4 结论

针对具有时间窗约束的无人集群协同任务分配问题,提出一种分布式任务分配算法DATW,其优化目标是最小化任务平均完成时间。仿真实验结果表明,DATW提出的任务再分配阶段将任务成功分配率提升了13.76%,并且所提算法可以适应各种通信拓扑,相比于ECNP算法,DATW和CBBATW在不同拓扑下性能表现稳定,同时DATW的平均任务完全分配率比CBBATW高21.94%,任务平均完成时间小24.25 s,因此获得的任务分配结果质量更好,性能更好。但文中对无人机和任务的一些参数进行了简化,并未考虑到实际环境中障碍物和威胁的存在,未来可以更接近实际地研究分布式任务分配算法,提升算法在现实环境下的实用性。