代理模型在飞行器多学科优化中的应用研究

蒋鲁佳，辛万青，张 鸣，王 威，陈红波

(北京宇航系统工程研究所，北京 100076)

0 引言

多学科设计优化是为解决复杂系统设计困难提出的概念,通过实现多个学科的自动设计和优化能够缩短产品研制周期、提高设计质量、降低研制成本,具有重要的研究意义和应用前景[1],尽管在很多领域得到了应用,并不断向规范化、商业化发展,然而,在多学科设计优化过程中,大量的计算、学科之间复杂的数据交互以及学科分析中非线性响应都会消耗大量的计算时间,从而降低优化算法的寻优效率以及优化结果的准确性。

代理模型技术通过构造近似函数可以将复杂的学科分析简化,从而避免了在优化过程中进行的极其耗时的多学科分析,从而降低了设计空间搜索的工作量。目前该技术已应用于风力涡轮机、巡航导弹头部外形、运输机机翼等优化设计中,并取得了较好的设计结果[2-4],此外,还有人提出了一些基于代理模型技术的优化算法,并验证该方法能够有效提升优化效率[5-6]。文中以飞行器多学科设计优化为例,探寻代理模型技术在其中应用的思路和方法。

1 代理模型原理

代理模型主要有多项式响应面模型、Kriging模型、径向基函数模型以及人工神经网络模型等。

1)多项式响应面模型

多项式响应面的前几项数学表达式为:

(1)

式中:xi为m维自变量x的第i个分量;β0,βi,βij为待定参数。

多项式响应面模型具有良好的可微性和连续性,易于实现优化,且可以通过系数判断各项对系统影响的大小[7],但是,在处理复杂程度较高的非线性问题时,多项式响应面模型预测和拟合的结果相对较差。此外,当建立模型的阶数较高时,过拟合的情况也有可能发生[8]。

2)Kriging模型

Kriging模型一般表示为:

f(x)=g0(x)+z(x)

(2)

式中:g0(x)视作模型中确定的部分,可用多项式来表示;z(x)为涨落,是一个均值为0、方差为σ2的随机函数。

Kriging模型处理复杂程度较高的非线性问题时,往往能够取得较好的结果,但是构造模型所消耗的时间较长,且由于算法复杂,较难通过软件实现,因此在实际使用中会受到一定限制[7,9-11]。

3)径向基函数模型

径向基函数的基本形式为:

(3)

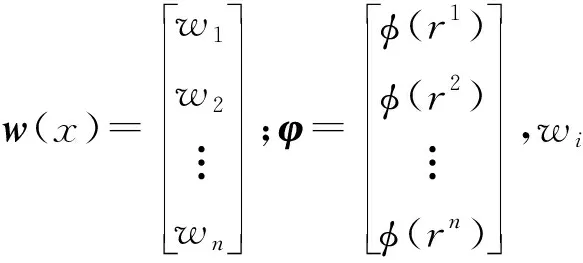
径向基函数模型的基本思路是首先确定一组样本点,然后再以这些样本点为中心,以径向函数作为基函数,通过把这些基函数线性叠加后计算待测点处的响应值[13],径向基函数模型会根据选取径向函数的变化而变化[14]。径向基函数模型是一个结构相对简单且计算量较小的代理模型[15-16]。

4)神经网络模型

神经元的结构模型如图1所示。

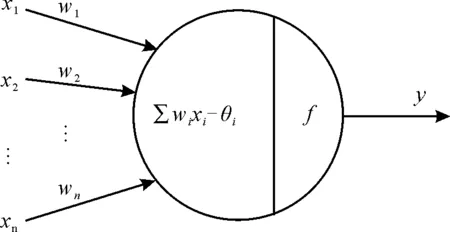
图1 神经元结构模型Fig.1 Neuron structural model

其中,wi为神经元与输入xi间的连接权重;θi为神经元的阈值;xi为神经元的输入信号;f为传递函数[17]。

神经网络模型使用输入和输出样本训练网络,通过调节各层神经元之间的权系数,实现模型的构建。神经网络模型建立的过程较其他代理模型更为简单,且可以通过实现并行计算来提高效率[18-20]。

2 飞行器多学科设计建模

文中以飞行器为背景,采用由最小起飞质量和最大射程组成的多目标函数作为飞行器总体多学科设计优化的目标函数,并将影响该目标函数以及设计方案可行性的几个专业,包括发动机结构及内弹道设计、飞行器外形设计、飞行气动设计、飞行器结构设计、质量参数分析、飞行轨迹设计、姿控设计以及飞行载荷设计作为实现飞行器总体多学科设计优化集成的学科[21]。各学科使用方案论证阶段的设计方法或能够满足该阶段要求的工程计算方法建立各学科设计模型。通过封装每个学科模型,使各学科成为具备独立分析和设计能力的模块。对建立的各学科设计模型的输入、输出数据进行分析,根据分析结果建立的飞行器总体多学科设计关系如图2所示。

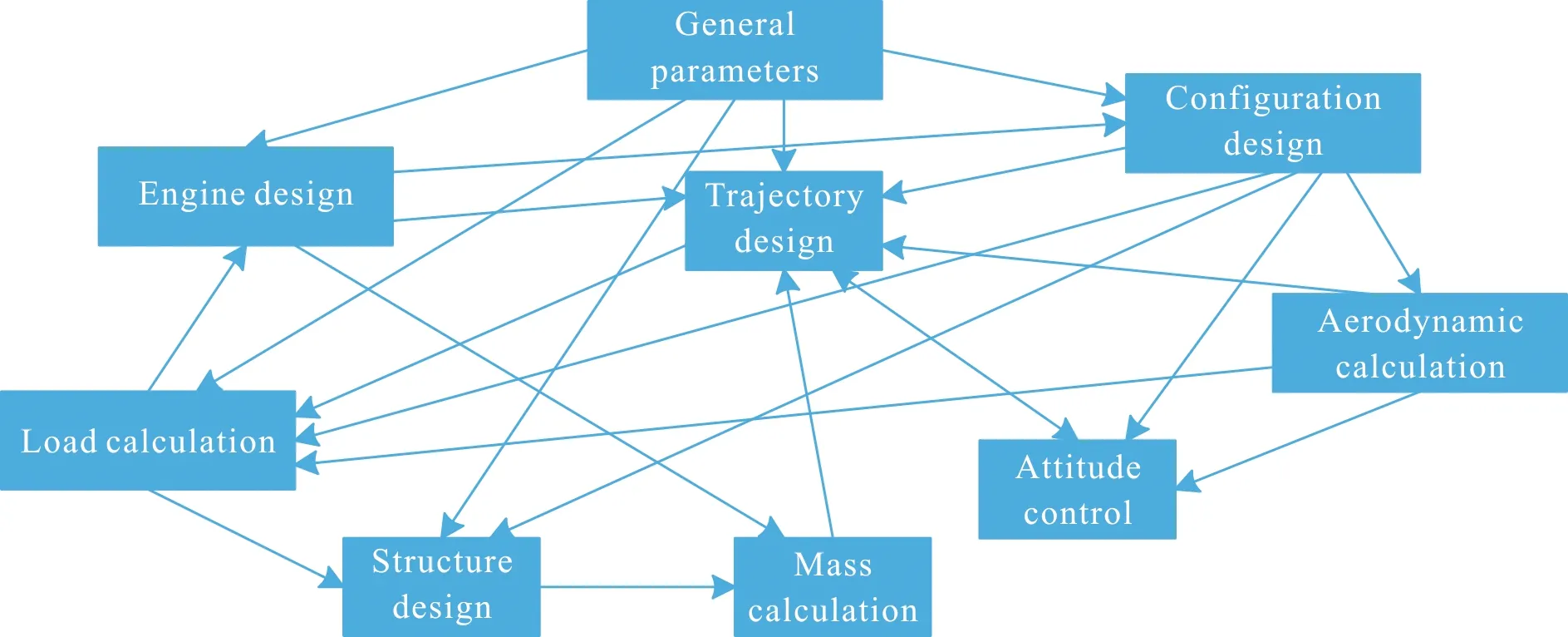
图2 飞行器总体多学科设计关系Fig.2 Relationship of aircraft system design subjects

从图2中可以看出多学科设计模型之间数据传递关系复杂,且存在多个反馈回路,而反馈回路会为飞行器总体多学科设计系统分析和优化带来较大的困难,为此,采用多学科设计优化耦合关系处理方法[22]进行解耦,解耦后的飞行器总体多学科设计关系消除了原系统中存在的反馈回路,如图3所示,系统在进行多学科分析时,只需由设计结构矩阵左上角的学科开始,依次进行分析即可[23]。

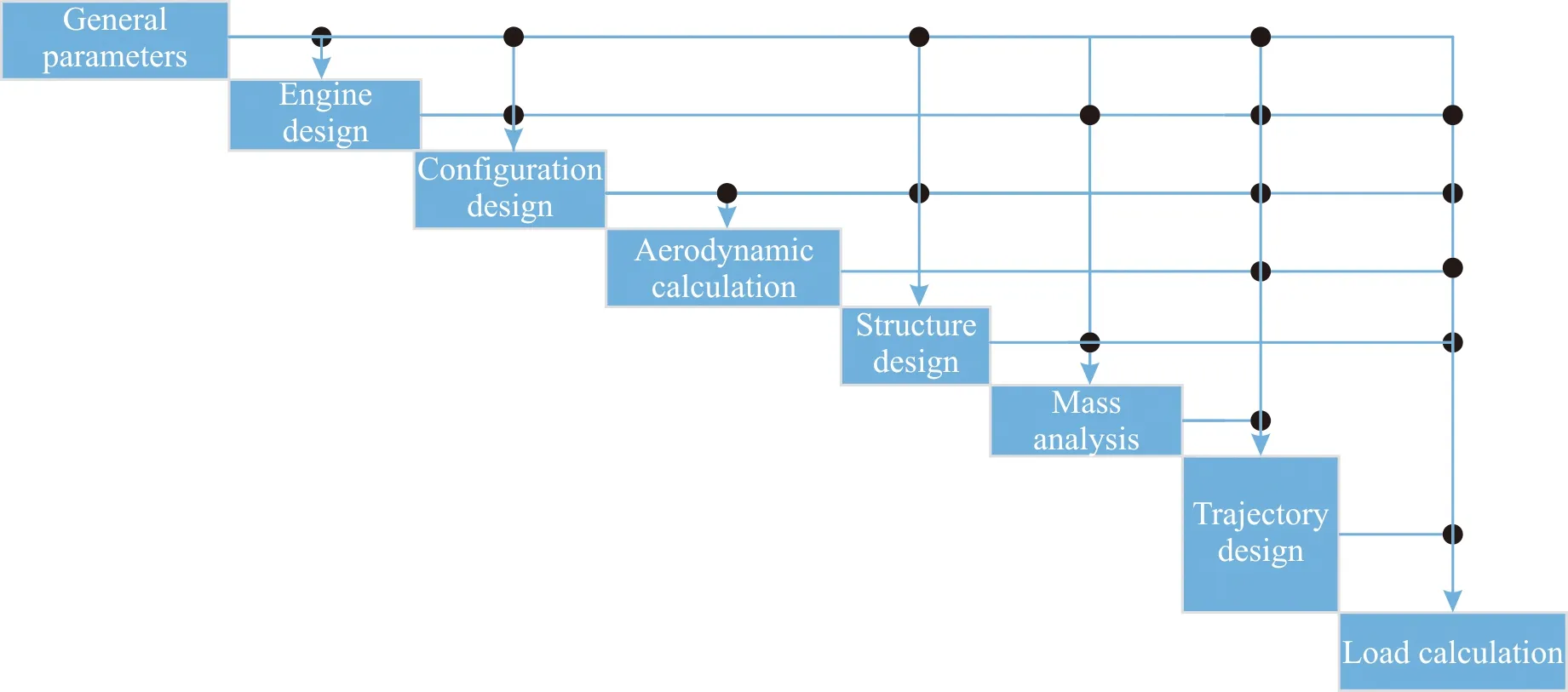
图3 调整后的飞行器总体设计DSMFig.3 DSM of aircraft system design after adjustment

使用iSIGHT-FD软件平台对飞行器总体多学科设计进行集成,集成的流程图和数据关系分别如图4和图5所示[24]。

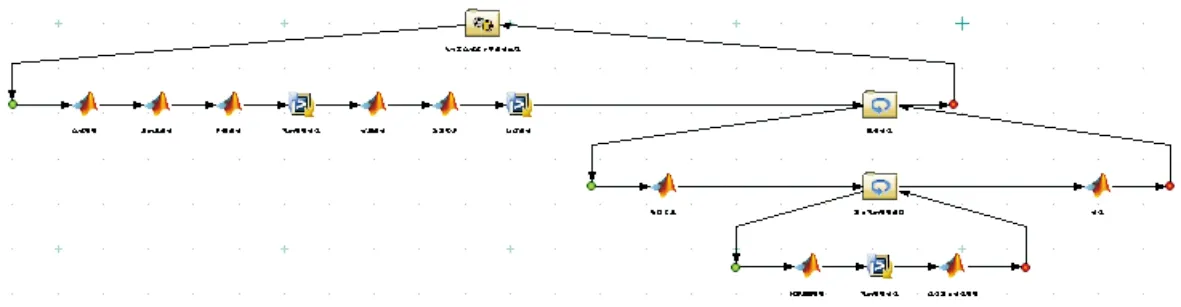
图4 飞行器总体多学科设计集成的流程图Fig.4 Flow chart of integrated aircraft system multidisciplinary design

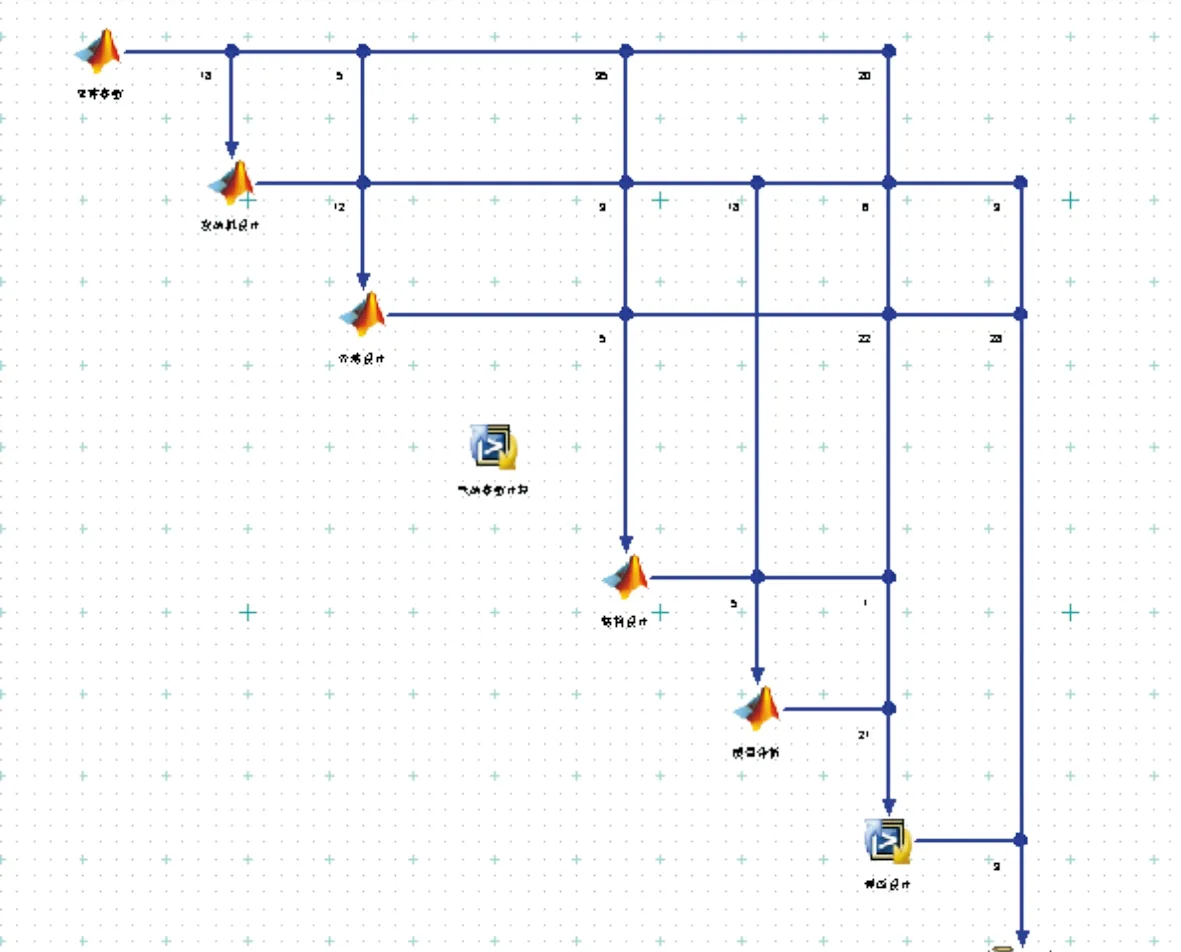
图5 飞行器总体多学科设计集成数据关系Fig.5 Relationship of integrated aircraft system multidisciplinary design

3 飞行器多学科设计优化

采用非支配遗传算法对建立的飞行器总体多学科设计优化模型的设计空间进行搜索,设置的种群数量为50,迭代次数为50,交叉概率为0.9,模型运行共耗时91 h9 min51 s,平均每次迭代用时约2 min11 s,得到的优化结果如图6所示,其中,纵坐标代表飞行器航程,横坐标代表飞行器起飞质量,图中隐去各坐标轴的度量(下同),图中蓝色的点即为Pareto解集,红色的点为满足各种约束条件的可行解集。

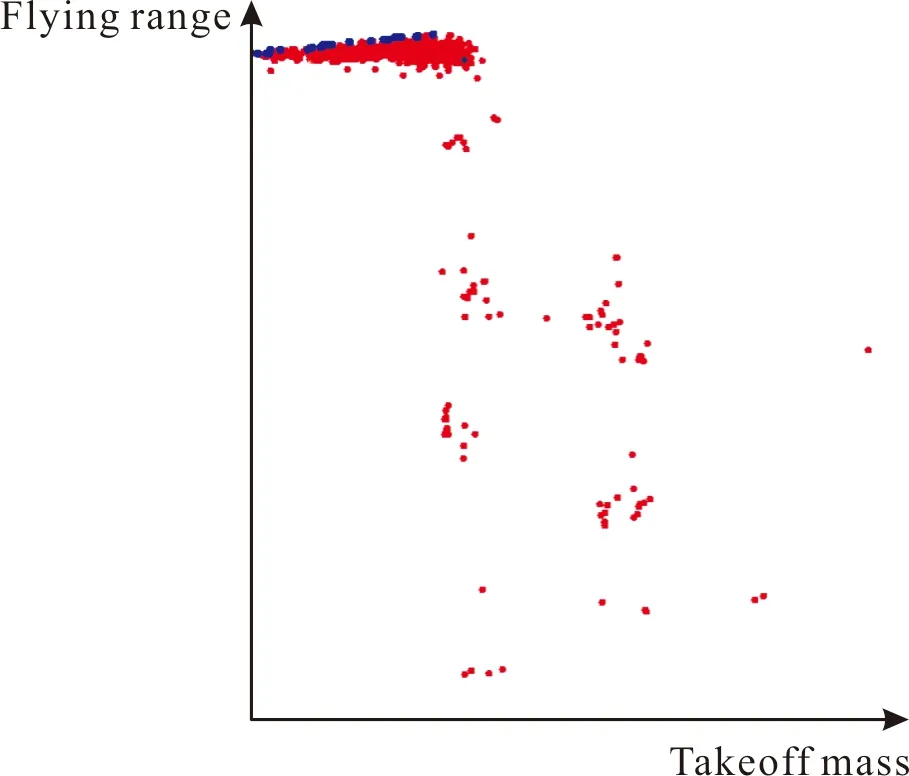
图6 优化结果Fig.6 Result of optimization

由以上优化结果可以看出,Pareto解集大致形成了一个Pareto面,由于Pareto解集中的点是由优化迭代范围内的非劣解集组成,因此,所有可行解包括优化的初始点都在这个Pareto面的右下方。在纵轴或横轴的任意位置画一条与横坐标轴或纵坐标轴平行的直线,该直线与Pareto面的交点就是在射程一定的条件下起飞质量最小的单目标优化问题或在起飞质量一定的条件下射程最大的单目标优化问题的最优解,Pareto解集也正是由这些“起飞质量一定的最大射程”或“射程一定的最小起飞质量”单目标优化问题的最优解组成。

通过对优化结果分析发现,飞行器总体多学科设计优化Pareto解集中两个端点设计变量的变化非常小,特别是一些外形参数变化都是在1～5 mm左右,这对于工程设计来说,只相当于在实际生产制造过程中产生的误差,最终得到的起飞质量和射程目标函数也非常的接近。经进一步分析可知,虽然耗费了大量的计算时间,进行了2 500次迭代计算,也得到了Pareto解集,但这仅是在2 500次迭代结果中得到的Pareto解集,迭代次数与设计空间上的可行解集相比还是非常有限的,尽管选择的非支配排序遗传算法在设计空间上具有全局搜索的能力,即理论上只要有充足的时间一定可以得到最优的Pareto解集,但是平均每次迭代需要耗费2 min11 s的模型,要进行全局搜索消耗的计算时间是非常巨大的。

对于建立的飞行器总体多学科设计优化模型存在的分析时间长、计算量大的问题,在当前计算机发展水平下,采用直接优化的方法获得全局最优解还存在一定的困难。为此,提出使用代理模型对复杂的多学科设计模型进行近似,并基于此开展优化设计的方法。

4 基于代理模型的飞行器多学科设计优化

将飞行器总体多学科设计优化模型中各学科分析模型作为一个整体建立代理模型,即在不考虑其内部各学科设计模型的输入输出以及各学科之间数据传递关系的条件下,建立飞行器总体多学科设计模型的代理模型。

首先使用了典型样本点分别采用响应面代理模型和神经网络代理模型对飞行器总体多学科设计模型进行近似。构造的四阶响应面代理模型和神经网络代理模型误差分析部分结果分别如图7、图8所示,其中,左侧“Total Error”列为构造代理模型所有对应的样本点平均误差归一化后的数值,右侧响应图则清晰的表达了代理模型响应变量偏离实际值的情况。

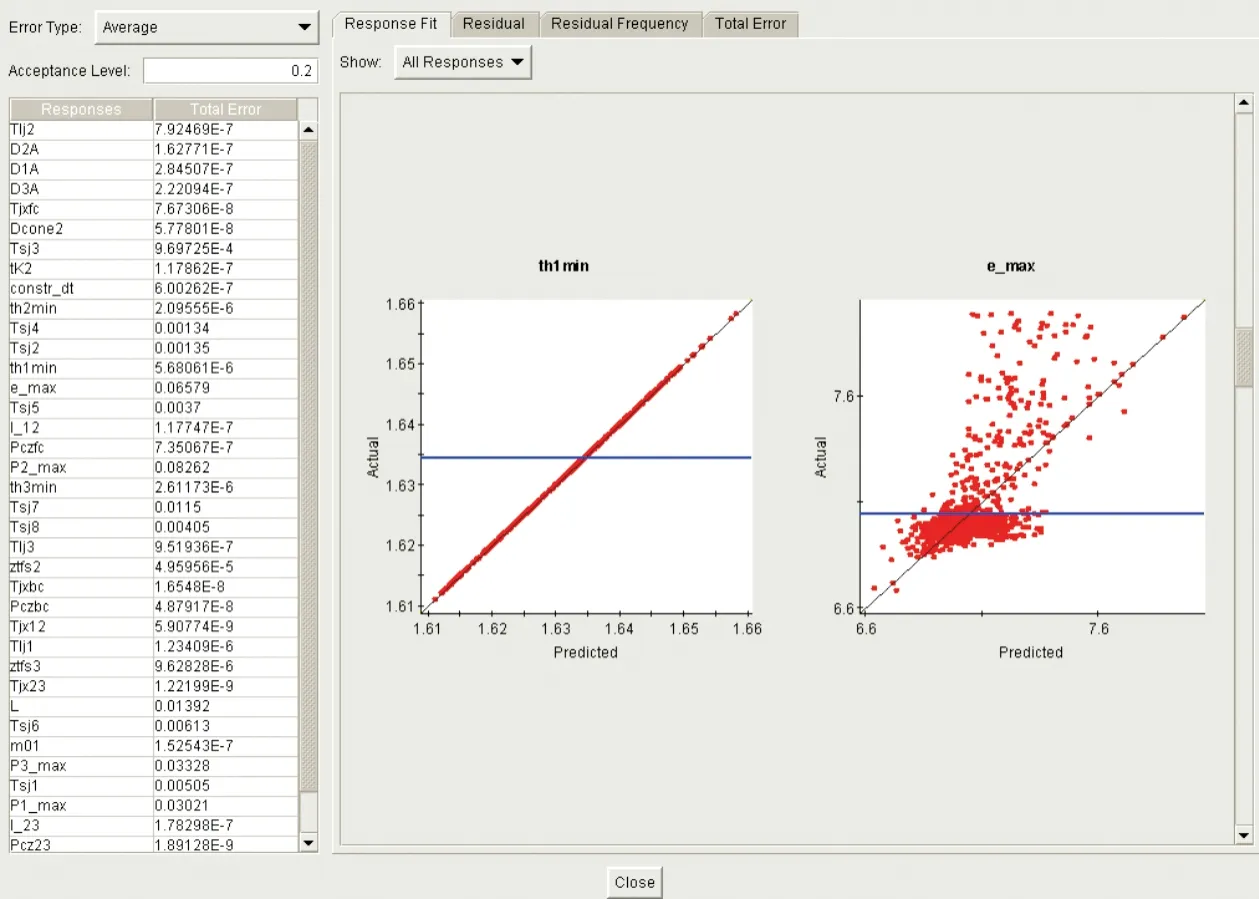
图7 四阶响应面代理模型误差分析Fig.7 Error analysis of quartic RSM

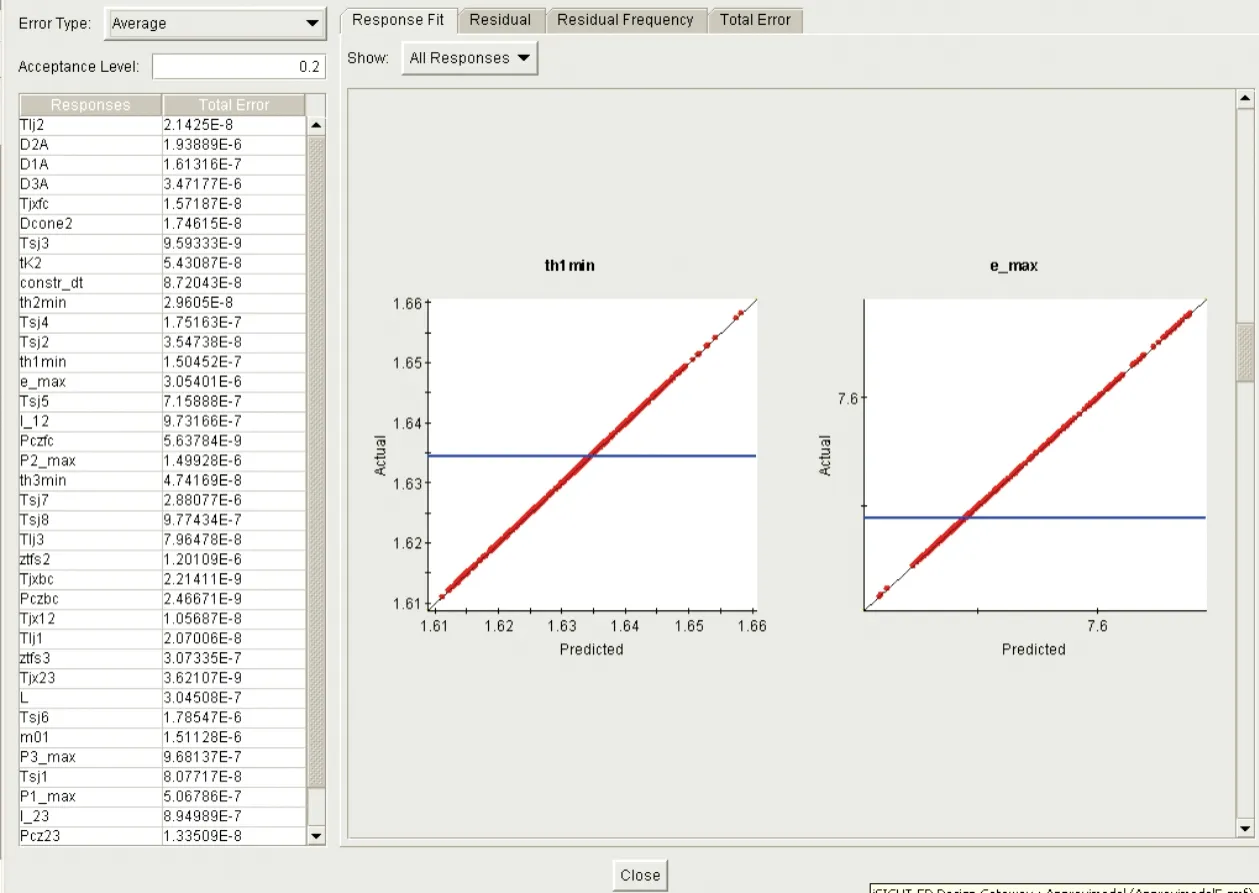
图8 神经网络代理模型误差分析Fig.8 Error analysis of RBF model

由以上误差分析对比可以看出,由于建立的飞行器总体多学科设计模型较为复杂,采用响应面法构造的代理模型误差较大,已经不能很好的反映原模型的真实情况;而采用神经网络构造的代理模型,虽然模型文件规模较大,但能够对样本点实现较好的近似,为此,选择神经网络代理模型实现对原模型的近似。

为了使样本点集具有良好的散布均匀性,并在取值范围内能够以较少的组合方式获得设计空间较全面的认识,使用最优拉丁超方设计方法进行了DOE(design of experiment)实验[25],并将该实验结果作为构造代理模型的样本点,并通过训练完成飞行器总体多学科设计神经网络代理模型的构造。然后,再对构造的代理模型进行优化,共耗时约2 h,进行了40 000次迭代,得到的Pareto解集如图9所示。从图中可以明显的看出起飞质量与射程的变化趋势,即随着装药量的增加,获得的射程也越大。其中,起飞质量在变化的过程中存在一个跳变,这可能是由于在构造代理模型样本点不够充分引起的。

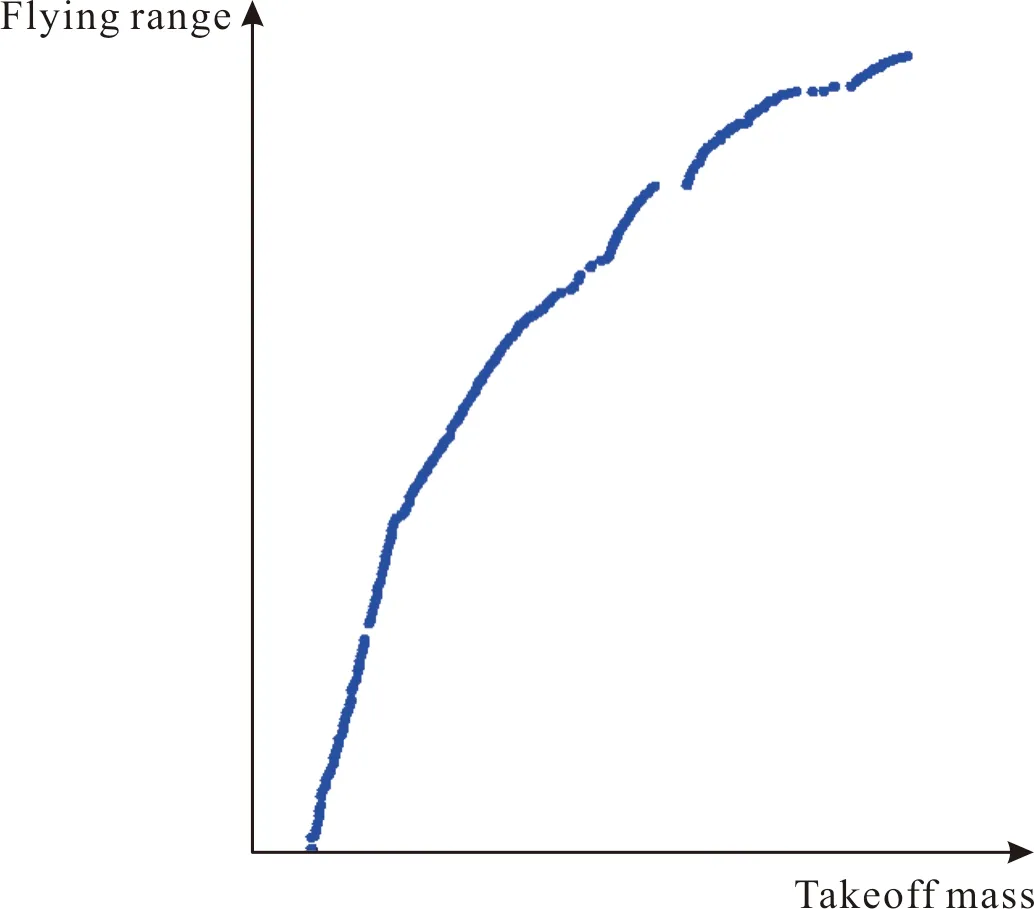
图9 代理模型优化结果Fig.9 Result of surrogate model optimization

在Pareto解集中选取了某起飞质量下的设计结果,并将该结果重新在飞行器总体多学科设计模型中进行分析计算,得到该起飞质量下的最大射程设计结果。通过比对发现,基于代理模型的飞行器多学科设计优化结果较原来的设计结果将最大射程提高了约6%,较好的说明基于代理模型的飞行器多学科设计优化在大幅提升优化效率的同时,还能够充分利用各学科模型相互作用产生出来的协同效应,进一步挖掘设计潜力[26-27]。

5 结论

文中针对飞行器总体多学科、多目标、多约束优化设计带来的计算困难问题,首先对复杂多学科优化问题计算困难进行了分析;其次提出一套使用代理模型技术实现飞行器总体多学科设计优化的思路和方法;然后提出使用代理模型将飞行器总体多学科设计模型作为一个整体进行近似的方法;最后提出了使用最优拉丁超方设计方法对设计空间进行DOE实验,并将实验结果作为建立代理模型的样本点的方法。优化结果表明,该方法可以有效降低多学科设计优化问题的复杂性,提高优化效率。

构造代理模型进行优化能够缩短计算需要的时间,虽然优化结果与原优化模型存在一定差距,但是随着构造代理模型的样本点增加,理论上能够在一定精度范围内反映设计变量与目标函数之间的大致关系,为设计人员权衡折衷、初步选择初始设计参数提供参考。此外,将代理模型的优化结果作为精确模型的初始设计点进行优化,也能够加快整个优化过程的收敛速度。