基于改进延伸奇异值分解包的滚动轴承故障诊断
胥永刚,杨苗蕊, 马朝永
(1.北京工业大学先进制造技术北京市重点实验室, 北京 100124;2.北京工业大学北京市精密测控技术与仪器工程技术研究中心, 北京 100124)
滚动轴承是机械设备中常用的零部件之一,对其进行状态监测和故障诊断具有重要的理论意义和工程价值[1]。基于振动信号的故障诊断方法主要包含特征提取与故障识别2个关键环节,目前常用信号处理作为特征提取的手段。设备振动信号的非线性和非平稳性为故障特征提取带来了困难,传统信号处理方法往往难以达到理想的效果[2-5]。
基于奇异值分解[6](singular value decomposition, SVD)的信号处理方法是一种有别于传统分析方法的非线性滤波方法,对于非线性和非平稳信号有着较好的效果。利用采集到的振动信号构造轨迹矩阵,然后进行奇异值分解,筛选分解后得到奇异值并重构出新的信号矩阵,可以实现信号的降噪[7],且重构信号没有相位偏移[8]。结合多分辨奇异值分解包[9]的分解结构和滚动轴承故障信号Hankel 矩阵的奇异值分布特性,黄晨光等[10]提出了延伸奇异值分解包(extended SVD packet, ESVDP)的故障诊断算法。该算法以奇异值分解算法为基础,实现了振动信号的分解,并以信号能量作为筛选指标,提出了有效分量的筛选准则。该方法具有强鲁棒性,极大地改善了奇异值分解包算法的模态混叠现象。但该方法中的2个关键参数——分解精度和分解层数是依靠经验值设定的,从而导致了分解结果存在不合理之处。与此同时,分解所得分量中还存在噪声成分,影响了故障特征的提取效果。
本文以延伸奇异值分解包算法为基础,利用频谱趋势对信号的频谱进行划分,以划分出的频带个数和各频带的带宽来自适应地设定分解精度和分解层数。同时,结合时域负熵指标,对各频带分量进行降噪处理,提高信噪比,最终实现了滚动轴承的故障诊断。
1 理论基础
本节主要对延伸奇异值分解包的理论基础进行介绍。同时,利用仿真信号来展示原算法的不足。
1.1 延伸奇异值分解包
设有离散信号X=[x1,x2,…,xN],可构造2K行的轨迹矩阵
(1)
式中K为分解精度,K≤2且K为正整数。
利用奇异值分解算法对轨迹矩阵XA进行分解,即
XA=USVT
(2)
式中:U、V为正交矩阵;S为XA的奇异值对角矩阵。设S中的奇异值为σ1,σ2,…,σ2K,且σ1≥σ2≥…≥σ2K,则S可表示为
S=[diag(σ1,σ2,…,σ2K)]T
(3)
由此,可以得到信号的2K个奇异值。保留排序为2i-1和2i的奇异值,将其余奇异值置零,以此得到新的奇异值矩阵
S′i=[0,diag(σ2i-1,σ2i),0]T
(4)
式中:0表示零矩阵;i∈[1,K]。
再利用新的奇异值矩阵进行重构,得到第1层的第i个分量信号矩阵
(5)
式中:R的上标表示了此分量所在的层数;下标i则表示此分量是该层的第i个分量。
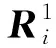
(6)
式中:α=max(1,n-2K+1);β=min(N-2K+1,n);m∈[2,N-1]。
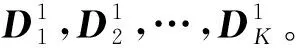

(7)
式中‖·‖L2表示L2范数。
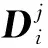

图1 延伸奇异值分解包分解结构Fig.1 Decomposition structure of ESVDP
1.2 延伸奇异值分解包的不足
如前所述,在延伸奇异值分解包中存在2个关键参数需要设定——分解精度和分解层数,而在原算法中这2个参数是依靠经验值进行设定的,从而导致了分解结果不合理。与此同时,分解结果中还存在噪声成分,影响了后续的特征提取和故障诊断。
为了直观地展示延伸奇异值分解包中的不足,构造信号x(t):
x(t)=[4+9sin(2faπt)+8sin(4faπt)]×
sin(2f1πrt)+[5+10sin(2faπt)+8sin(4faπt)]×
sin(2f2π)+[6+9sin(2faπt)+
8sin(4faπt)]×sin(2f3πt)
(8)
式中:fa=15 Hz;f1=300 Hz;f2=500 Hz;f3=700 Hz。
设置采样点数为2 048,采样频率为2 000 Hz。加入信噪比SNR=1.5的高斯随机白噪声后,该信号的波形和频谱如图2所示。

图2 仿真信号x(t)的波形及其傅里叶谱Fig.2 Simulation signal and its Fourier spectrum
利用ESVDP算法处理式(8)所示仿真信号。根据文献[8]中提出的关键参数设定范围,设置分解精度K=3,分解层数J=5,得到的分解结果如图3所示。

图3 延伸奇异值分解包分解结果Fig.3 Decomposition results of the simulation signal by ESVDP
在图3所示的分解结果中,出现了频谱混叠的现象。与此同时,以300 Hz和500 Hz为中心的2个频带同时出现在了分量1中,且其中的信息变得残缺不全,这无疑会影响到后续有效信息的提取。
基于以上几点不足,本文提出了改进ESVDP算法,利用频谱趋势自适应地设置关键参数,并结合时域负熵对分解得到的结果进行降噪处理,提高信噪比。
2 改进ESVDP算法
改进ESVDP算法是以延伸奇异值分解包算法为基础,通过频谱划分结果中的频带个数确定分解精度,并利用频谱划分结果中的频带带宽确定分解层数,实现信号的自适应分解。同时,通过时域负熵指标提取分解结果中的有效成分,剔除无用的噪声成分,为后续的故障诊断奠定基础。具体流程如图4所示。

图4 改进ESVDP算法流程Fig.4 Flow chart of improved ESVDP method
具体步骤为:
1) 参数设定。预先设置频谱趋势估计中的b值和步骤4)中涉及的迭代阈值。
2) 利用关键函数[14-16]对信号进行频谱趋势估计。对振动信号x(t)进行快速傅里叶变换(fast Fourier transform, FFT),得到其幅值谱A(f)和相位谱φ(f)。再计算A(f)的傅里叶变换函数,即关键函数
C=FFT(|A(f)|)
(9)
截取关键函数C的前b个点,进行傅里叶逆变换。变换结果近似频谱的趋势,称为趋势成分Tc(f),即
Tc(f)=iFFT(Cb)
(10)
式中Cb为C的前b个点。
需要指出的是,式(9)中的|A(f)|是一实数离散序列,对其进行傅里叶变换不会得到x(-t),而是一个新的函数C。傅里叶逆变换时,b的取值越大,信号趋势成分中包含的细节信息越多;反之则细节信息越少。因此,可以根据信号的复杂程度选取b值,建议b的取值范围为[5,15]。
3) 以趋势成分中的极小值点作为分界点,将频谱划分为若干个频带。划分出的频带个数即为分解精度K的值,同时记录每个频带的带宽和位置作为带宽范围ai,i∈[1,K]。
4) 对振动信号进行奇异值分解,同时以能量作为筛选指标筛选最终分解结果。计算每层中第i个有效分量信号的总能量Ei和该信号频谱中位于带宽范围ai之外频率的信号能量EDi,i∈[1,K]。若EDi与Ei的比值大于1%,则将此分量作为新的待分解信号;反之则将此分量信号保留为最终的分解结果。
5) 为了提高算法效率,在步骤1)中预先设置了迭代阈值。当需要进行下一层分解时,先将当前的分解层数与迭代阈值进行比较。若当前分解层数小于迭代阈值,则进行下一层分解;反之则循环终止,将此分量保留为最终分解结果。分解层数越多,对计算速度和幅值的影响就越大,经多次实验,笔者认为迭代阈值的设定范围为[5,15]时的计算效果较好。

(11)

(12)
式中1≤i≤j。

(13)

3 改进ESVDP算法的仿真分析
为了直观地介绍改进ESVDP算法的实现过程,利用此算法对式(8)构造的仿真信号进行分解。
计算信号的关键函数,取其前15个点得到信号趋势成分,并以趋势成分中的极小值为分界点划分频谱。
将频谱划分为了5个频带,即分解精度K=5。同时记录下这5个频带的带宽作为带宽范围ai,i=[1,5],如图5所示。
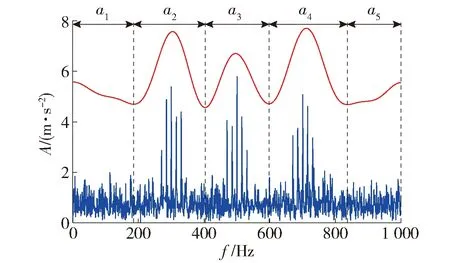
图5 频谱趋势划分结果和带宽范围Fig.5 Spectrum trend and bandwidth threshold of the simulation signal
利用式(1),将原始信号构造成行数为10的轨迹矩阵,然后进行奇异值分解,得到第1层的5个有效分量频谱,如图6所示。

图6 第1层有效分量的频谱Fig.6 Effective components of level 1
由于这5个有效分量的总能量和位于带宽范围ai之外频率的信号能量比值均大于1%,故而将其作为下一层的待分解信号,重复上述分解过程。当分解层数为7的时候,该层中第1个和第2个有效分量的能量比值小于1%,如图7所示,将其保留为最终分解结果,其余3个分量继续进行分解。

图7 傅里叶频谱带宽对比Fig.7 Comparison of Fourier spectrum bandwidth
图8中展示了最终的分解结果。这5个分解结果从上到下分别对应了图5中频谱趋势划分结果的第4个、第2个、第3个、第1个、第5个频带。从图8中可以看出,前3个分解结果包含了有效的信息,后2个分解结果只包含了噪声干扰。
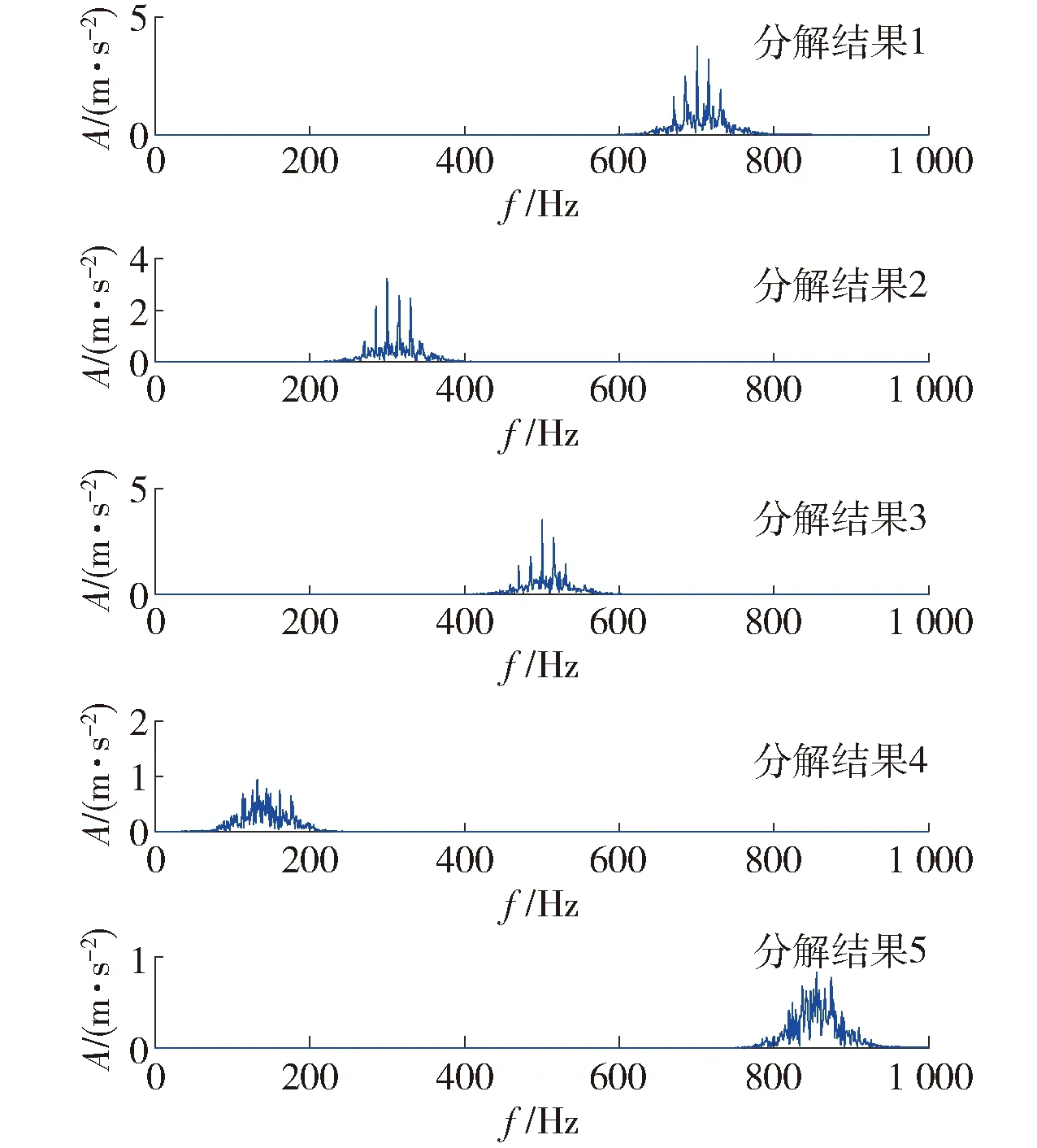
图8 分解结果的频谱Fig.8 Decomposition results of the simulation signal
结合步骤5)中所描述的方法,通过计算分解信号的时域负熵指标最大值,减少了分解结果中的噪声干扰,结果如图9所示。

图9 降噪后分解结果的波形和频谱Fig.9 Decomposition results after denoising
对比图8、9可以看出,各个分解结果中的无效成分已经基本被去除掉了,突出了有效信息,有利于后续的特征提取和故障诊断。
4 改进ESVDP算法的实验测试
为了进一步验证所提出方法的有效性,采集了滚动轴承故障模拟实验台上的振动信号,实验台如图10所示。

图10 滚动轴承故障实验台Fig.10 Rolling bearing test rig
利用该实验台采集了6307滚动轴承外圈故障振动信号,电机转速为1 496 r/min,采样频率为15 360 Hz,采样点数为8 192。经计算,该轴承的外圈故障特征频率为fo=76.88 Hz。
图11为采集到的振动信号和根据其趋势成分进行频带划分的结果,其中黑色虚线为所划分的边界,红线为频谱趋势。如图所示,信号波形中的周期性冲击并不明显,存在较多噪声成分。

图11 实验信号及其频谱划分Fig.11 Experimental signal and its spectrum trend
由于噪声较大,其中的有效信息被湮没,给后续的故障诊断带来了困难。利用提出的改进ESVDP算法对此振动信号进行处理。根据图11所示的频谱划分结果,可知分解精度K=5,同时获得了5个带宽范围ai,i∈[1,5]。基于此,得到的分解结果如图12所示。

图12 实验信号分解结果Fig.12 Decomposition results of the experimental signal
从图12所展示的分解图中不难看出,前2个分量中出现了周期性的冲击成分,同时其频谱中包含了明显的边频带。而第3~5个分量中的有效信息较少,因此在后续的分析中,只展示了前2个分量的处理结果。
结合第2节中介绍的算法步骤5),计算分解结果的时域负熵指标,以此来选取需要保留的特征信息,从而实现分解结果的降噪处理。
图13展示了前2个分量的时域负熵指标,其中红色标星处为最大值。

图13 分量1和分量2的时域负熵Fig.13 Time domain negative entropy of decomposition result 1 and 2
降噪处理后的分量1和分量2的波形、频谱,以及包络谱(0~800 Hz)如图14所示。
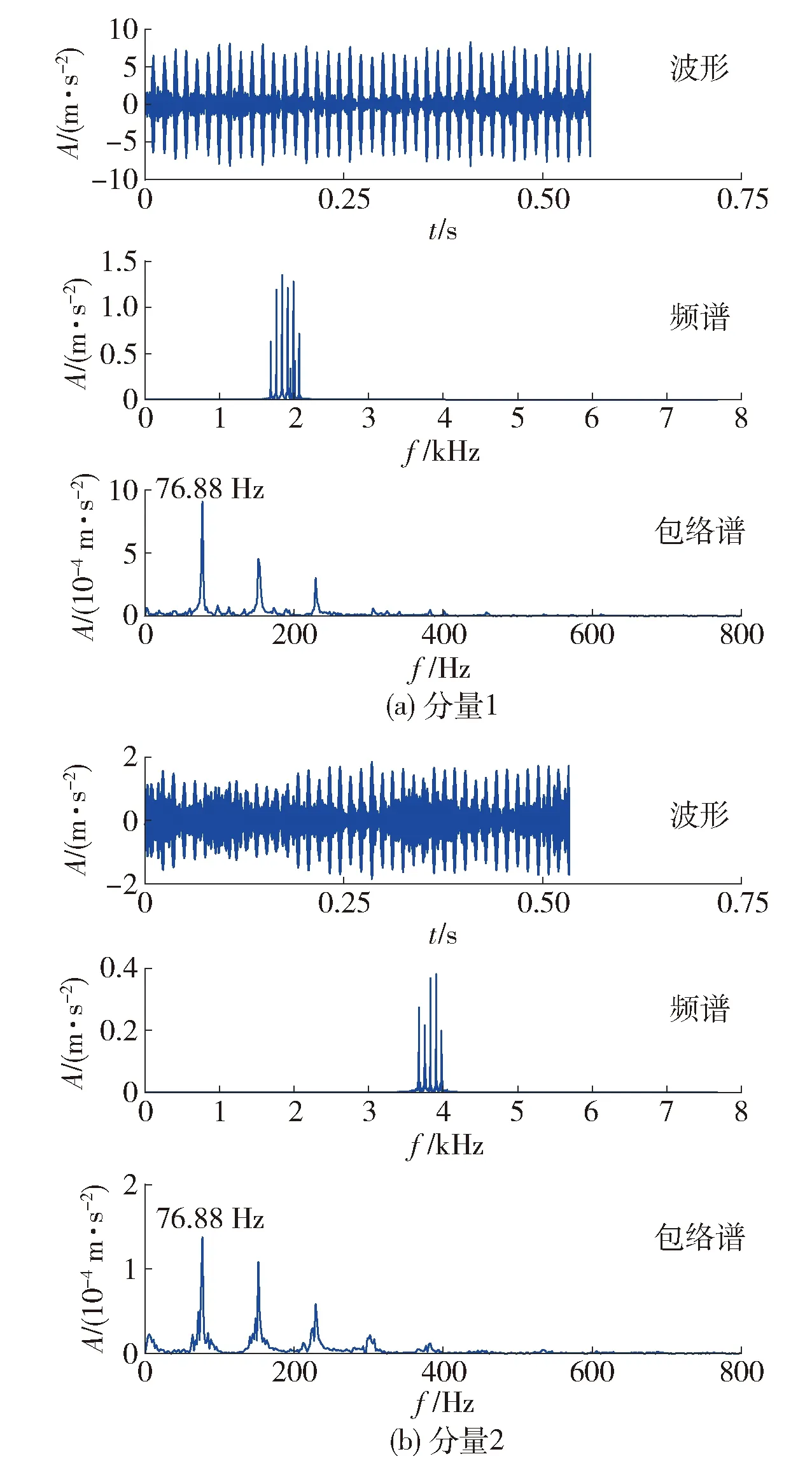
图14 降噪处理后的实验信号分解结果Fig.14 Decomposition results of the experimental signal after denoising
降噪处理后的分量1和分量2的包络谱中,低频部分均出现了明显的峰值,对应着6307轴承外圈故障特征频率及其倍频。因此,可以诊断出轴承外圈发生故障。
5 结论
1) 通过关键函数的重构得到振动信号的频谱趋势成分,实现了频带的划分,从而自适应地设定了分解精度和带宽范围,并通过带范围确定了分解层数。
2) 结合时域负熵指标对分解结果进行了降噪处理,有效地去除了干扰成分,提高了信噪比,为后续的故障诊断打下基础。
3) 结合仿真和实验对该方法进行了验证。结果表明该方法可以从复杂的振动信号中准确地提取出故障特征,最终实现了滚动轴承的故障诊断。

