双碳目标下退役农机产品拆解规划与EOL 决策集成优化

袁 刚 ，李洪波 ，罗建强 ，张宗毅 ，杨印生 ，孙俊华

（1. 东南大学机械工程学院,南京 211189；2. 江苏大学中国农业装备产业发展研究院,镇江 212000；3. 吉林大学生物与农业工程学院,长春 130022；4. 江苏省农业农村厅农机行业发展处,南京 210036）

0 引言

随着农业智能化智慧化的快速发展，产生了大量退役农机产品。据2022 年全国农业机械化统计年报，2021年国内拖拉机与联合收割机的保有量分别达到2 173.06万和223.78 万台，若按国家规定的农机产品服役年限10～15 a 计算，未来数年农机产品退役数量极其惊人。退役农机产品中包含着大量的可再生资源，若不能有效再生利用将会造成极大的资源浪费和环境污染，农机装备拆解回收对提高农业资源利用和促进农业可持续发展具有重要意义[1]。近年来，国家相继出台了相关政策以促进退役农机产品回收、拆解、再制造等。《中国制造2025》提出全面推行绿色制造，大力发展再制造产业，实施高端再制造、智能再制造，促进再制造产业持续健康发展[2]。2011 年国家发改委办公厅发布的《关于深化再制造试点工作的通知》，明确提出要开展拖拉机、联合收获机等农业机械再制造试点，探索完善可再制造旧件回收和再制造产品销售渠道[3]。2019 年农业农村部印发了《关于加快推进农业机械化转型升级的通知》，指出农业机械化转型升级和绿色低碳发展是我国农业机械化全程全面高质量发展的重要内容[4]。2020 年农业农村部印发《农业机械报废更新补贴实施指导意见》，提出加快老旧农业机械报废更新进度，进一步优化农机装备结构，促进农机安全生产和节能减排[5]。因此，退役农机产品拆解规划已成为农业废弃物资源化利用和农机再制造领域的研究热点。

拆解是将产品、总成或部件等装配体进行解体的作业或活动，是产品多次拆卸作业的结果[6]，同时也是实现产品再利用的前提。拆解序列规划可以优化零件拆解顺序，实现目标值最优化，而EOL (end-of-life)决策可以对拆卸下来的零部件进行决策分类，从而实现资源回收、零件重用以及减少环境污染的目的[7]。拆解序列规划方法的研究主要分为基于图论的拆解序列优化[8]、基于CAD 模型的序列优化[9]、基于数学规划的拆解序列优化[10]、基于启发式算法的拆解序列优化[11]、基于模糊理论的拆解序列优化[12]。拆解序列规划主要使用特定的图形表达工具来反映拆解的动态过程，例如AND/OR 图[13]、拆解树[14]、Petri 网[15]、有向图[16]及解释结构图等。拆解规划的求解主要以启发式方法为主[17-18]，如遗传算法、人工蜂群算法、蚁群算法等。相关研究结果表明，农用履带拖拉机可再制造零部件占整机部件约60%，而再制造拖拉机价格仅为新机价格的50%～60%[19]。农机再制造评价从技术性、经济性、环境性、资源性等方面开展[20-21]，运用多智能优化算法和多属性决策方法从多角度多层次实现了废旧农机产品再制造的综合性能评价[22-23]。

现有的农机拆解研究主要以数学规划方法和元启发式算法获得Pareto 拆解方案，但对于复杂装备，传统算法很难得到高质量的解。因使用状况的复杂性和零部件失效的不确定性，使得农机产品拆解再制造集成优化不同于其他机械产品，因此，本文提出考虑再制造成本和碳排放成本的拆解序列规划与EOL 决策集成优化模型，以提高农业资源综合利用率和促进农机装备绿色可持续发展[24-25]。首先，考虑拆解再制造的综合收益构建拆解决策集成优化模型，所构建的目标函数包含收购成本、再制造产品收入、拆解成本、EOL 操作成本、碳排放成本。其次，提出一种改进的人工蜂群算法对所构建的模型进行求解。最后，通过联合收割机电机拆解再制造案例分析验证模型的可行性和有效性。

1 拆解再制造集成优化模型

1.1 问题描述

拆解再制造集成优化DRIO(disassembly remanufacturing integrated optimization)是产品回收过程中拆解规划和EOL 操作的集成优化。拆解序列是待拆解产品完成拆解过程的作业顺序。EOL 操作包括再利用(reuse)、再制造(remanufacturing)和回收(recycle)[25-26]，决定如何处理每个拆卸下来的部件或子组件。再利用指组件或零件在简单的处理后可直接再次使用。再制造是指零部件经过翻新修复达到使用功能。回收是对不满足再利用/再制造的零件回收其原材料。

假设待拆解产品由M个子组件构成，子组件集合为S=(s1,s2,···,si,···,sM)，子组件对应的零件集合为C=(c1,c2,···,cj,···,cN)且M＜N。子组件与零件间的关系可以用结构矩阵描述为。优先矩阵用于描述子组件/零部件间的优先约束关系，子组件的优先约束矩阵为

若子组件si优于sp拆卸，则Gip=1，否则Gip=0。

零部件的优先约束矩阵为

若零件cj优于cq拆卸，则Hjq=1，否则Hjq=0。

EOL 操作的设计变量为

为便于研究，根据文献[27-28]，引入以下假设：

1) 再制造产品需求是关于售价p和保修期限w的函数[28]，定义为D(p,w)=ηp-αωθ，其中α,θ,η为正实数。

2) 折旧率是收购价格v和服役年限x的函数，定义为R(v,x)=kvσxγ,σ,γ,k为正实数。

3）EOL 成本是关于服役年限x和EOL 操作xm的函数，定义为c(x,xm)=cr(x-xm)ψ。其中，cr是单位时间再制造成本，元，且cr＞ 0,ψ＞ 0[29]。

4）零部件的失效在统计上是独立的，且零部件都可拆解。

5）再制造产品和新产品的故障率一致。

1.2 DRIO 模型构建

1.2.1 再制造产品销售收入

使用Cobb-Douglas 函数对销售价格进行建模。对于服役年限为x的产品，销售价格p对保修期限w和改善因子u（0≤u≤1）的函数关系，销售价格p(x,w,u)为

其中p0为新产品的售价，元；L为产品期望寿命，a；kw和ku为非负参数；a和b为常数，且a＞0,b＞0。

则再制造品的销售利润为

式中p为单位再制造产品售价，元；D(p,w)为再制造产品的需求量。

1.2.2 废旧产品的收购成本

单位回收成本可通过市场反馈数据或产品年限的折旧率估计。产品回收价格vp和产品服役年限x的函数关系为

式中R(v,x)为产品的折旧率；k0为常数。

1.2.3 拆解成本

拆卸成本受拆解顺序影响，通过拆解时间可以评估拆解成本，而拆解时间与产品的使用年限呈正相关，拆卸时间包括拆解操作时间、拆卸工具更换时间和拆解方向改变时间，拆解成本计算如下：

式中cdt表示单位时间的拆解成本，元；ntl表示零件cl拆解的标准化时间，h；tdc为拆解工具更换平均时间，h；Elk为二元变量，如果拆解零件cl和ck使用相同的工具，则Elk=1，否则Elk=0；tdd为拆解方向改变的平均时间，h；ξlk为二元变量，如果拆解零件cl和ck方向改变，则ξlk=1，否则ξlk=0。

1.2.4 再制造成本

根据再制造经验，再制造成本随产品服役年限和改善因子的不同而变化，再制造成本E(x,u)与改善因子u和x的函数关系，则为

1.2.5 碳排放成本

拆解再制造过程中的环境成本主要为碳排放成本，根据文献[14]可知，单位碳排放成本(Cec)包括以下几方面：机器耗电的碳排放(μ·wrp·Tec)、再制造材料消耗crc、化学品消耗ccc和能源消耗cen，计算式分别为

式中 μ为电力碳排放因子(0.928 kg/(kw·h)，IPCC 2006)；wrp为机器作业功率，kW；Tec为机器作业时间，h；ar,br,Cr是碳排放功能参数；d为需求率，且d＜m；ζ为再制造部件数量，且ζ＞0；βζ表示再制造部件的实际比例。

根据以上分析可知，拆解再制造的总利润为

利润最大化问题的数学模型为

约束条件为

式中D(p,w)为再制造产品的需求量；R(v,x)为产品的折旧率；c(x,xm) 为EOL 成本，元；xm为EOL 操作；x为服役年限，a；Δ为预算，元；ϵ 为部件使用年限上限。

2 DRIO 模型求解

本文所提的DRIO 模型集成了拆解序列规划和EOL决策联合优化，计算复杂，最优解获得难度大。人工蜂群算法(artificial bee colony algorithm,ABC)是一种群体智能优化算法[30]，主要用来解决NP-Hard 问题的组合优化，具有参数少、计算性能好等优点[30]，广泛应用于制造业的优化求解。因此，本文选用IABC 算法对提出的DRIO 模型进行优化求解。经典ABC 最早用于求解连续优化问题，而DRIO 模型的求解属于离散优化问题，为此，本文提出一种改进的ABC 算法进行拆解再制造联合决策优化，算法流程如图1 所示，包括种群初始化，雇佣蜂阶段，守望蜂阶段，侦察蜂阶段，其中雇佣蜂阶段和守望蜂阶段需要判断蜜蜂所在蜜源的适应度值。算法运行参数，最大迭代次数为Tmax=50，种群规模PS=100，蜜蜂开采上限为200，每次计算运行20 次。

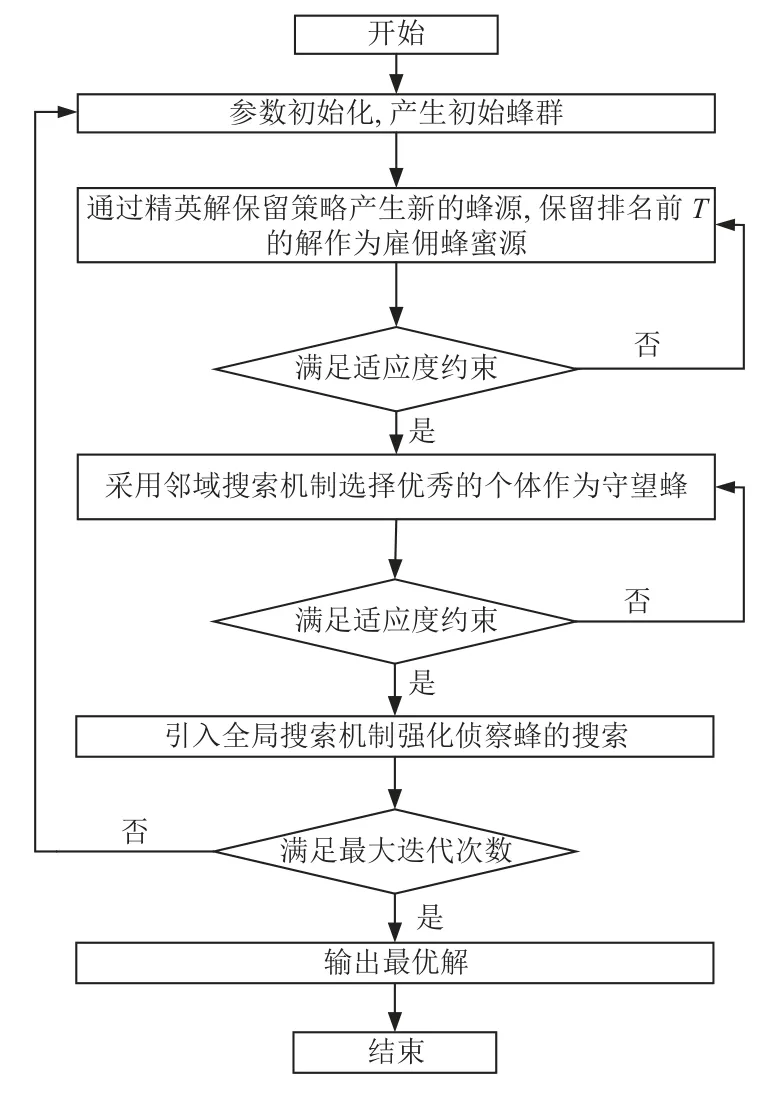
图1 改进人工蜂群算法流程图Fig.1 Flow chart of improved artificial bee colony algorithm(IABC)

2.1 种群初始化

种群初始化是群优化算法的关键环节，直接影响算法的收敛速度和最终解的质量。在没有相关先验知识的情况下，通常使用随机初始化来生成初始群体。随机初始化能保证初始种群在解空间中均匀分布，但会影响算法的收敛速度。为得到高质量的初始解，本文基于logistic 映射生成初始解。假设种群P含有SN个个体，每个个体用向量Xi=(xi,1,xi,2,···,xi,D)表示，D表示解空间的维度，本文采用双链表结构编码，记为x={v1,v2}，v1表示拆卸序列，v2表示EOL 操作方式，logistic 映射生成初始解的计算公式如下：

其中i表示果蝇个体，i=1,2,···,SN；j表示空间维度，j=1,2,···,D；xmax,j和xmin,j分别代表第i个个体第j维变量的上下界；yij为逻辑映射变量；rand(0,1)为[0,1]之间的随机数。

2.2 雇佣蜂阶段

在经典ABC 算法中，雇佣蜂在食物源附近寻找浓度最高的位置。为了在不影响种群多样性的前提下加快收敛速度，将目标函数值从小到大排序，排名前T(T≤Tmax(目标函数最大值))的目标函数值所对应的寻优解作为精英解保留。为了加强探索以及避免局部最优，随机选择个体k及其邻域调整雇佣蜂的搜索方向，则精英解的位置由搜索方程vij生成：

式中xe,j为在维度j中随机选择一个精英解；xk,j(k∈{1,2,···,SN})表示从种群j维中随机选择的个体；xkbest,j表示第k个个体的j维邻域范围内目标函数值最优的食物源位置；φi,j为[-1,1]之间的随机数。

2.3 守望蜂阶段

守望蜂通过选择机制从雇佣蜂的食物源中随机挑选寻优位置。为了使高质量解的位置有较大概率被守望蜂选中，采取基于适应度的邻域搜索机制增强收敛能力，越优秀的个体被选择的概率越大，适应度较好的个体有更多的机会被选择参与寻优。第i个个体参与寻优的选择概率Pi的计算式如下：

式中ri为根据适应度降序排列的第i个个体的等级。

2.4 侦察蜂阶段

侦察蜂的作用是识别并排除被守望蜂过渡搜索，原始的侦察蜂阶段采用轮盘赌方法但容易陷入局部最优，为了解决此问题，在侦察蜂阶段引入全局搜索机制，其计算式如下：

式中ti为当前迭代次数；φij为[-1,1]内的随机数；ωmax和ωmin表示侦察蜂位置调整的最大和最小百分比。

3 案例分析

为了验证所构建的DRIO 模型和改进蜂群算法求解的可行性和有效性，本文选用联合收获机的电机作为拆解再制造案例进行分析，所有算法在MATLAB2020 软件上进行编程实现，计算机配置为Intel(R) Core(TM),i5-1155G7 @2.5GHz (8CPUs)。

3.1 数据获取

电机是回收再制造的主要农机组件之一，其通用性强和回收再制造利润高。以沃得4LZ-9.0CR 联合收获机的电机拆解再制造为例，电机零部件的三维结构如图2所示零部件的详细信息如表1 所示。各零部件回收价值根据当前回收市场行情进行修正，EOL 处理数据采用文献[14]提出的产品回收评估方法估算，拆卸方向改变时间为3 s[30]，拆卸工具改变时间5 s[31]，拆卸人工费25 元/h[32]，材料回收详细参考数据见表2，根据Petri 网构建的拆解顺序图如图3 所示。

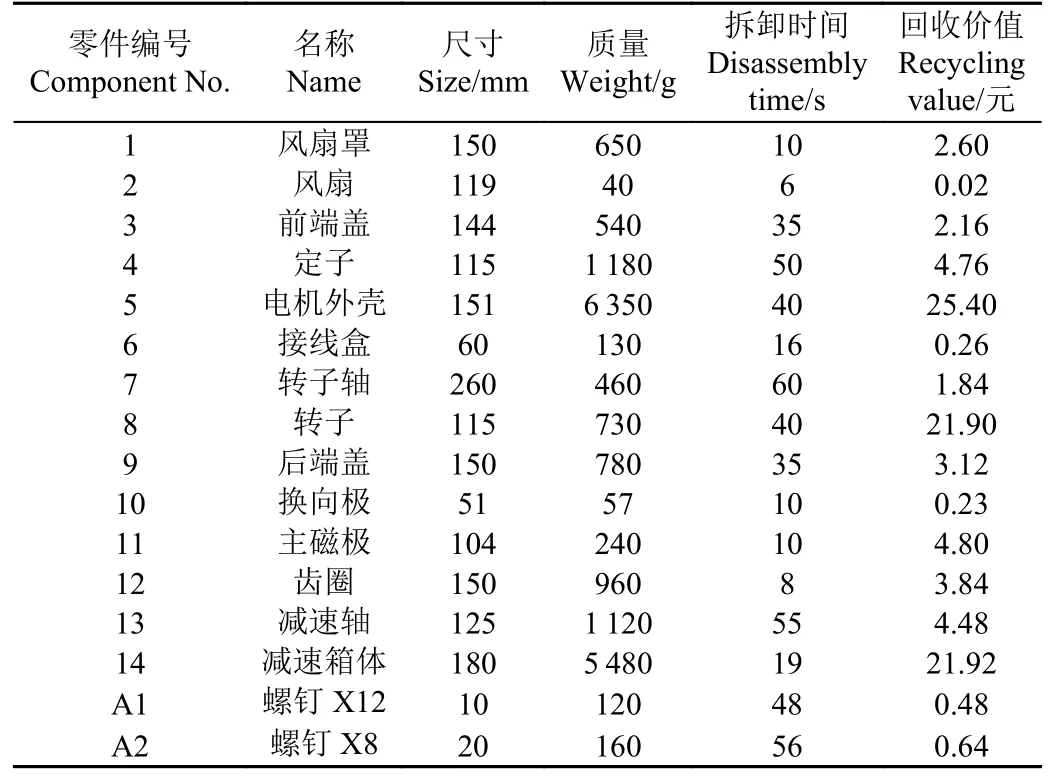
表1 4LZ-9.0CR 电机零部件详细信息Table 1 Details of motor parts for 4LZ-9.0CR

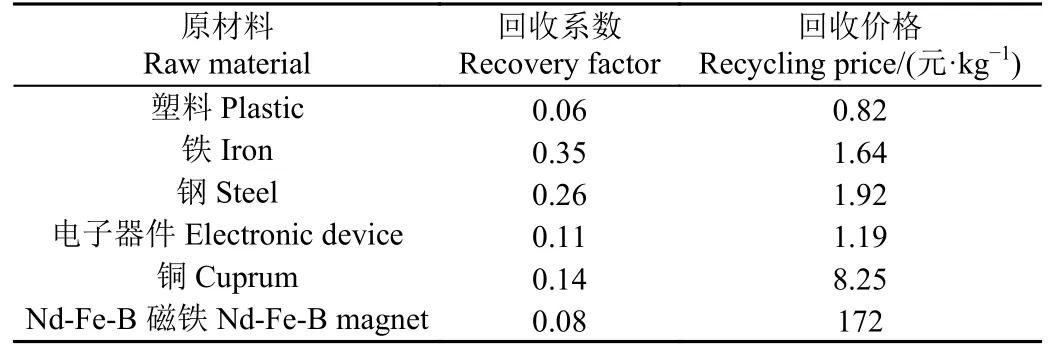
表2 原材料回收参考数据Table 2 Raw material recovery reference data

图2 4LZ-9.0CR 电机三维结构Fig.2 The motor 3D structure of 4LZ-9.0CR

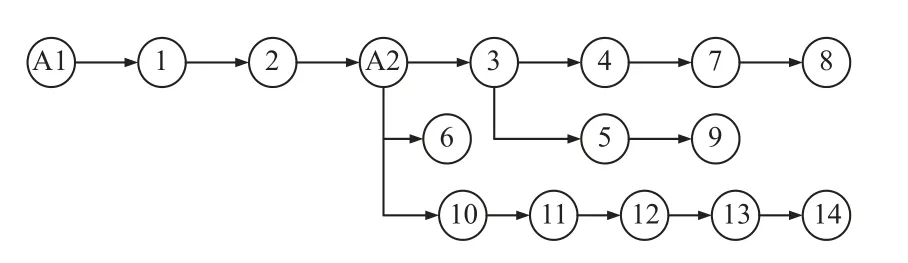
图3 4LZ-9.0CR 电机拆解顺序图Fig.3 Sequence diagram of motor disassembly for 4LZ-9.0CR

3.2 结果与分析

通过IABC 算法求解DRIO 模型得到一系列Pareto解，如表3 所示，其中方案3 和方案4 为目标函数值的最大最小值，分别为124.5 元和114.3 元。电机拆解再制造的最优解方案3 的信息如表4，零件的拆解顺序为A1→1→2→A2→6→3→4→7→8→5→9→10→11→12→13→14。对于方案3 的EOL 决策，零件集{A1,1,A2,6,10 }执行报废回收操作；{3,5,9,12,14}执行再利用操作；{2,4,7,8,11,13}执行再制造操作。为更直观反应拆解再制造过程，图4 给出了方案3 的拆解序列与EOL 决策顺序图，箭头指向拆解执行方向，圆圈线型表示不同的EOL决策，再利用、再制造和报废回收部件分别占总零件的37.5%、31.25%和31.25%。

表3 IABC 算法获得的拆解方案Pareto 解集Table 3 Pareto solution set of disassembly scheme obtained by IABC algorithm

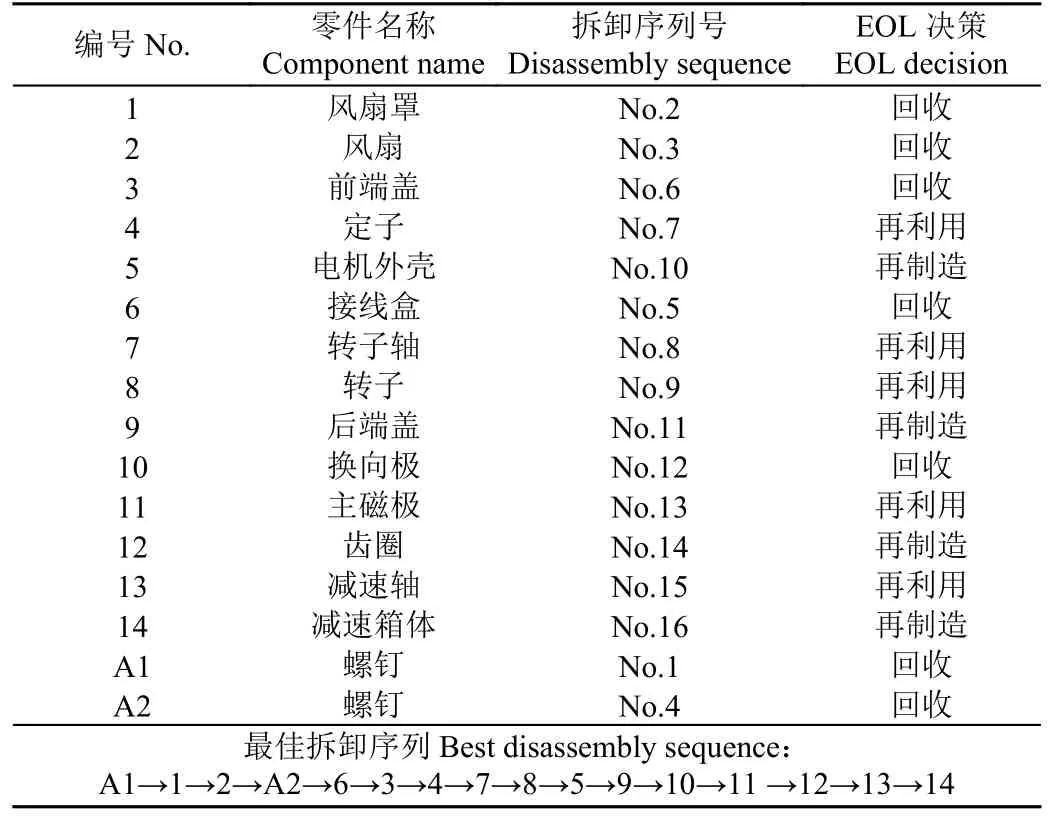
表4 方案3 的拆解再制造决策Table 4 Disassembly and remanufacturing decision of scheme 3

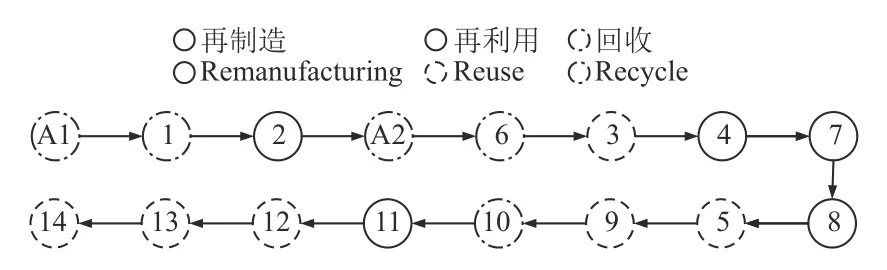
图4 电机拆解序列与EOL 决策Fig.4 Motor disassembly sequence and EOL decision

3.3 对比试验分析

为了验证本模型方法的有效性，引入3 种不同拆解再制造模型进行对比分析，结果如表5 所示，其中，DRIO模型考虑拆解再制造混合效益，DRIO-D 模型对所有零部件原材料回收，DRIO-R 模型将所有的零部件进行再制造。考虑再制造的DRIO 和DRIO-R 模型的碳排放成本约为DRIO-D 模型的50%，说明考虑拆解再制造比完全报废减少碳排放约50%。DRIO-R 模型的再制造成本约为DRIO 模型的2 倍，但是总利润仅为DRIO 模型的45%，说明零件全部采取再制造操作不一定实现利润最大化。DRIO 模型的总利润为124.5 元，相对于DRIO-D模型的47.2 元和DRIO-R 模型的56.3 元，分别提高了62.1%和54.8%，以上分析表明，零部件再制造率的增加会减少总利润，因此，适当的拆解再制造联合优化可提高总收益。

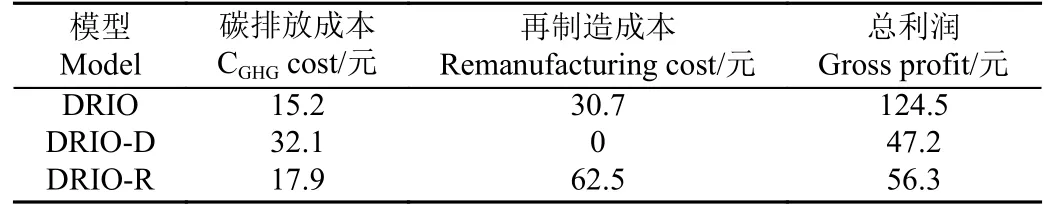
表5 不同模型下的求解结果对比Table 5 Comparison of solution results under different models

为了进一步验证改进人工蜂群算法的有效性，将IABC 与人工蜂群算法（ABC）[33]、蚁群算法（ACA）[34]进行对比分析，ABC 和ACA 的算法参数设置分别见文献[32]和文献[33]。对于算法性能的比较，选用特征指标超体积反应非劣解收敛性，间距度量反应解的分散程度，各算法的求解结果如表6 所示。从表6 可以看出，IABC 算法相比于经典人工蜂群算法的求解时间缩短了19.3%，可行解数量增加了28.6%，相比于蚁群算法的求解时间缩短47.8%。IABC 求解的非劣解个数最多且求解速度快，超体积值2.813 大于ABC（2.695）和ACA（2.377），同时间距度量值优于其他2 种算法。以上分析表明，IABC 在求解质量和求解效率上表现优越。

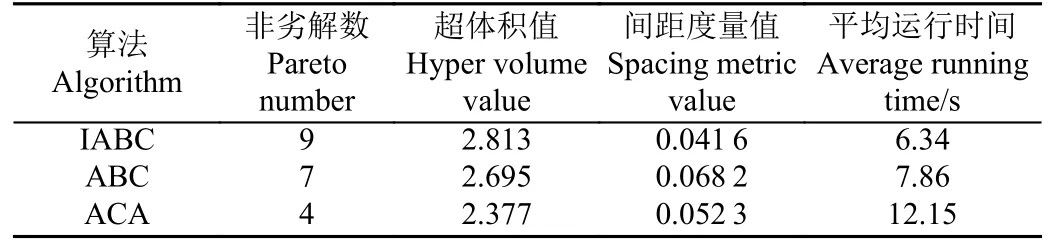
表6 不同算法的求解结果Table 6 Solution results of different algorithms

4 结论

本研究提出了一种集成拆解规划和EOL 决策方法，建立了考虑产品回收利润和碳排放成本的DRIO 模型，将其运用到拆解再制造的集成决策优化中，并通过改进的人工蜂群算法求解所构建模型，最终确定最佳拆卸顺序和EOL 决策。通过案例分析对本文的模型和算法进行了验证，同时将所提出的方法与DRIO-D，DRIO-R 两种产品回收策略进行了对比分析，结果表明所提DRIO 模型的经济效益相较于DRIO-D 和DRIO-R 模型，分别提高了62.1%和54.8%，而DRIO 和DRIO-R 模型的碳排放成本均比DRIO-D 模型减少约50%。IABC 算法相比于传统人工蜂群算法，求解时间缩短了19.3%，可行解数量增加了28.6%。本研究可为拆解回收企业提供利润高且节能效果好的综合性拆解决策方案，进一步揭示了废旧产品回收利用以及再制造的经济价值和促进碳减排的社会意义。本研究仅分析了农机产品回收再制造过程的经济效益及碳排放成本，后续将围绕智能农机装备全生命周期碳排放展开进一步研究。