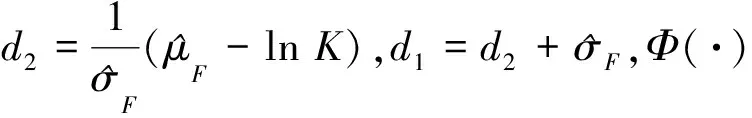一类分数金融资产价格过程的近似解及其期权定价

王继霞,肖晓芳

(河南师范大学 数学与信息科学学院,河南 新乡 453007)

在金融一体化的背景下,描述各金融资产价格之间的长记忆性是金融时间序列分析中的一个重要研究内容.关于时间序列长记忆性的研究最早可以追溯到1951年,HURST[1]基于800多年的数据对尼罗河的长期水流特征进行了研究,发现尼罗河的水位特征具有自相似性和长记忆性.此后,人们在股票、利率、汇率等许多金融时间数据中也发现了这种现象,并对这种现象进行了更深入的研究.比如BAILLIE[2]讨论了对长记忆波动过程及其在金融中的应用;BERAN[3]和GRANGER等[4]研究了一类平稳过程的长期相关性等.RATTIKAN[5]研究了分数过程驱动的分数Hull-White模型,代替了由标准布朗运动驱动的传统Hull-White利率模型.此外,RATTIKAN[6]将几何布朗运动驱动的Black-Scholes模型改进为分数Black-Scholes模型,并验证了分数Black-Scholes模型可以更好地拟合IBM历史股票数据.

近年来,关于我国金融市场长相依性特征的研究也很多,比如,李志生等[7]根据有效市场理论及分形市场假说,应用序列相关检验及R/S检验法分析研究出我国股票市场具有显明的长相依性.苑莹等[8]运用一系列检验方法研究了我国的股市收益率和成交量的长相依性特征.肖炜麟等[9]对金融市场数据进行了实证研究,发现金融资产价格具有长相依性.张跃军等[10]研究了原油价格波动,证明原油市场波动存在结构性变化和长记忆特征.长记忆性侧重探究价格序列本身在较远时间间隔时是否仍具有持续依赖关系.将时间序列长记忆性特征分析运用于金融环境,可以准确把握金融市场的运行规律并构造符合实际的精确预测模型.

由于金融环境的不确定性,使得金融资产的价格过程呈现出长记忆特征,这意味着经典的布朗运动在某种程度上不能很好地描述资产价格过程,很多已有的研究表明利用分数布朗运动能有效捕捉资产价格长相依这一现象.然而,由分数布朗运动驱动的金融模型却在金融市场中存在套利机会.为解决这一问题,本文针对金融环境中存在的长记忆现象,构建具有半鞅性质的分数高斯过程驱动的金融资产价格模型,并得到模型解的闭式表达式及其期权定价公式.本文所构建的模型在金融市场中不存在套利机会,这给人们研究期权定价问题带来了方便.

1 金融资产价格模型与近似模型构建

设{Xt,t≥0}为金融资产的价格过程,满足由分数布朗运动驱动的如下随机微分方程,

(1)

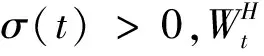
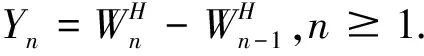
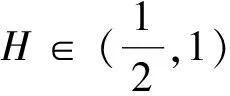
本文所研究的模型是很多金融中著名模型的推广,如下面的注释.

注1(a)当函数γ(t)=0时,模型(1)为金融中著名的分数Hull-White模型.

(b)当函数α(t)=0且σ(t)=0时,模型(1)为分数Black-Derman-Toy模型.

(c)当函数α(t)=α,β(t)=β,σ(t)=σ,且γ(t)=0时,其中α,β,σ为常数,则模型(1)为金融中的分数Vasicek模型.

(d)当函数α(t)=α,β(t)=β,γ(t)=γ,且σ(t)=0时,模型(1)为分数Dothan模型.

因此模型(1)是一类分数金融资产价格过程[11].

由文献[12]知,分数布朗运动可以表示为:

(2)

其中Γ(·)是伽马函数,(Wt)t≥0是标准布朗运动,且

(3)

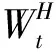
(4)

(5)

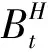
下面将给出模型(5)的由半鞅驱动的近似模型,并讨论该模型的解.对∀ε>0,定义

(6)

其中{Wt,t≥0}是标准布朗运动.注意到下面的积分

因此

(7)

令

(8)

则式(7)可表示成

(9)

(10)

这里‖·‖表示L2(Ω)中的范数,C(H)为仅依赖于H的常数.由式(10)可得,当ε→0时,

(11)

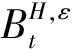
下面构建模型(5)的近似模型,对∀ε>0,考虑如下随机微分方程:

(12)

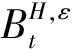
下面的定理1给出了模型(12)中解的表达式.

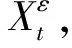
(13)

其中

(14)

证明由式(9)可得,

(15)

把式(15)代入式(12)可得:

(16)

显然模型(16)是由标准布朗运动{Wt,t≥0}驱动的线性随机微分方程,且是如下形式的线性随机微分方程:

dX(t)=(m(t)+n(t)X(t))dt+(p(t)+q(t)X(t))dWt.

(17)

已知m(t),n(t),p(t),q(t)是t的连续函数,则式(17)的解是唯一存在的.

由文献[17]可知,式(17)的解的形式如下:

(18)

其中

(19)

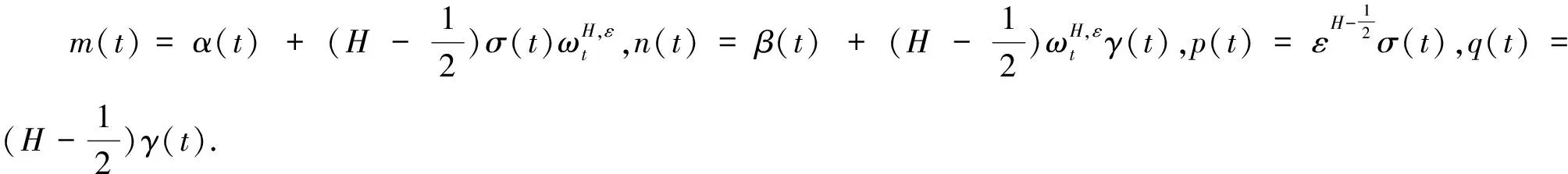
(20)

其中

(21)

证毕.

2 模拟研究

其中N是区间[0,t]上的分割区间个数,由于{Wt,t≥0}是标准布朗运动,故有

其中{ξk,k=0,1,2,…,N-1}是独立同分布的标准正态随机变量.

模拟步骤如下:

(i)参数设定:设定T=1,分别设定H=0.125,0.375,0.625,0.875,ε=0.062 5,0.125 0,0.250 0,0.500 0.

(ii)Ni为区间[0,ti]上分割区间数,i=1,2,…,500,生成标准正态随机数g1,g2,…,gNi-1,计算

(22)

(iv)模拟上述程序20次.

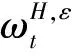
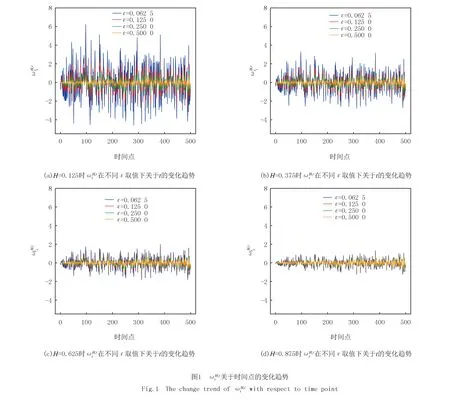
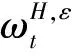
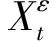
(23)

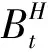
(24)

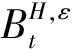
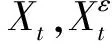
(25)

此外,由定理1可得模型(24)的解为:

(26)

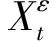
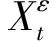
3 基于近似模型的几何平均亚式期权定价

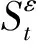
(27)

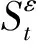
由半鞅驱动的金融模型在金融市场环境中是无套利的,下面研究模型(27)的期权定价问题.设K为敲定价格,T是到期日,则看涨期权的支付为(AT-K)+,看跌期权的支付为(K-AT)+.这里AT表示在执行时间[0,T]上金融资产的平均价格,其计算公式为:

(28)

假设无风险利率为常数r,市场无摩擦,期权在到期日才能执行,则几何平均亚式看涨期权和看跌期权的定价公式分别为:

C(K,T)=e-rTE[(AT-K)+].

(29)

和

P(K,T)=e-rTE[(K-AT)+].

(30)

下面的定理给出了期权定价公式的表达式.

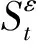
(31)

和

(32)

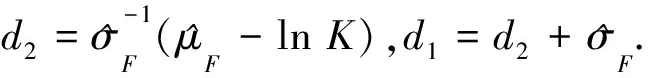
证明由式(15)知,模型(27)可以写为:

(33)

所以模型(27)在风险中性测度下的解为:

(34)

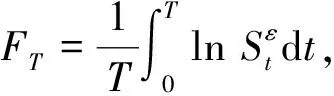
(35)

(36)

(37)

(38)