基于离散元法的川产法半夏仿真参数标定

谢宇鸿，王金栋，陈 燚，吴展扬

（西南交通大学机械工程学院，四川 成都 610031）

0 引言

半夏是一种典型川产中药材，在镇咳祛痰、抗肿瘤方面具有明显疗效，法半夏则是半夏通过生石灰、甘草汁等进行炮制后的加工品。半夏的粉碎细度会影响其有效成分的析出[1]，采用离散元法进行半夏粉碎的仿真分析，有利于揭示半夏的粉碎机理，对粉碎设备研磨副的研制、提高半夏粉碎细度具有指导意义。

离散元法（Discrete element method，DEM）是将研究对象视为由大量颗粒组成的离散系统，通过研究颗粒间的接触关系、受力情况和运动状态等进而获取研究对象的宏观和微观物理量信息的研究方法。经过数十年的发展，离散元法已经广泛用于工农业领域[2-4]。半夏的粉碎加工是一个典型粉体加工过程，半夏与半夏、半夏与研磨副间具有复杂的相对运动和碰撞，因此适于采用离散元法进行仿真分析。

为确保离散元法分析的准确性，需确立研究对象准确的物性参数[5-8]。物性参数主要分为物体的本征参数和物体间的接触参数，本征参数（包括泊松比、剪切模量和密度等）为物体自身固有的特性参数；接触参数（包括碰撞恢复系数、静摩擦系数和滚动摩擦系数）为表征两物体接触特性的参数，由于复杂的接触特性通常无法通过直接测量获取，因此需要对接触参数进行标定。目前，众多国内外学者开展了有关离散元仿真参数标定的研究。张勇等[9]通过台架试验和理论计算获取绿豆与不同材料（钢板、有机塑料板和橡胶）间的滑动摩擦系数和碰撞恢复系数。于庆旭等[10]基于离散元仿真和台架试验，对三七种子间、三七种子与ABS 塑料板间的接触参数进行了标定。刘敏等[11]通过实际试验获取紫花苜宿种子的本征参数，以休止角为指标标定了紫花苜宿种子与钢板的接触参数。田剑锋等[12]通过修改滚动摩擦系数，使仿真试验所得的堆积角与实际堆积角接近的方法获取党参种子间的滚动摩擦系数。戴念祖等[13]、吴孟宸等[14]、马文鹏等[15]以堆积角相对误差为指标进行无物料的接触参数标定。鹿芳媛等[16]、RORATO 等[17]，XIA 等[18]运用图 像处理 技术，以堆积角为指标分别对水稻、砂石和湿煤粉进行参数标定。邢洁洁等[19]、BAHRAMI 等[20]，采用离散元法对特定土壤进行仿真参数标定。GHODKI等[21]采用侧壁坍塌试验对大豆的离散元仿真参数进行标定。YE 等[22]运用BP 神经网络进行颗粒的参数标定。ROESSLER 等[23]考虑到最优参数的不确定性，通过对比堆积试验、侧壁坍塌试验和抬升试验，发现不同试验方法和指标结合能够有效减小最优参数组合的数量。综合国内外研究，目前对半夏的接触参数标定鲜有涉及，导致无法建立准确的半夏离散元仿真分析模型，从而对半夏高效粉碎加工及有效成分提取带来较大影响。

本文以干燥的川产法半夏（以下简称半夏）为研究对象，进行半夏的接触参数标定。采用EDEM软件建立半夏的离散元模型，并结合物理试验和仿真试验标定半夏与粉碎设备研磨副材料（4Cr13 不锈钢）间的接触参数；利用堆积试验和图像识别方法获取半夏堆积角及误差，采用响应面法（RSM）构建误差与接触参数的数学模型；以误差最小为目标，通过萤火虫算法（FA）求解半夏间最优接触参数组合；采用侧壁坍塌试验进行参数组合准确性的试验验证。

1 材料与离散元模型

1.1 材料的本征参数

半夏的整体形状为稍扁斜的半球形，下端钝圆较光滑，顶端有凹状茎痕，茎痕周边密布点状根痕，实物如图1 所示。随机选取100 粒半夏，采用分度值为0.02 mm 的游标卡尺测量半夏的外形尺寸，统计得半夏的直径为11.70～15.16 mm，高度为8.14～11.64 mm。采用检定分度为0.1 g 的电子天平进行称重，将半夏置于WH9020A 型电热恒温干燥箱（杭州聚同电子有限公司），105 ℃烘干至恒重，计算法制旱半夏含水率6.25%～9.63%。采用精度为1 mL的量筒，通过液浸法测量半夏的密度，统计得半夏密度为963～1 153 kg/m³。

图1 半夏实物

采用压缩试验测试半夏的弹性模量、泊松比和剪切模量。将半夏切割为高度5 mm，直径8 mm 的圆柱体试样，采用TMS-PRO 研究型食品物性分析仪（美国FTC 公司），使用直径为10 mm 的圆形探头，沿试样的轴线方向，按设置的加载速度和加载时间施加载荷，试验重复5 次，并记录半夏在压缩过程中的载荷-位移数据。根据公式（1）计算半夏的弹性模量

式中：

E——弹性模量，Pa；

σ ——最大压应力，Pa；

ε1——半夏的纵向线应变。

根据公式（2）计算半夏的泊松比

式中：

μ——泊松比；

ε2——半夏的横线线应变。

根据公式（3）计算半夏的剪切模量

式中：

G——剪切模量。

4Cr13 不锈钢的相关材料参数通过查表可得。结合压缩试验、EDEM 材料数据库及相关物料参数[24-27]，本研究设定半夏及4Cr13 不锈钢参数如表1 所示。

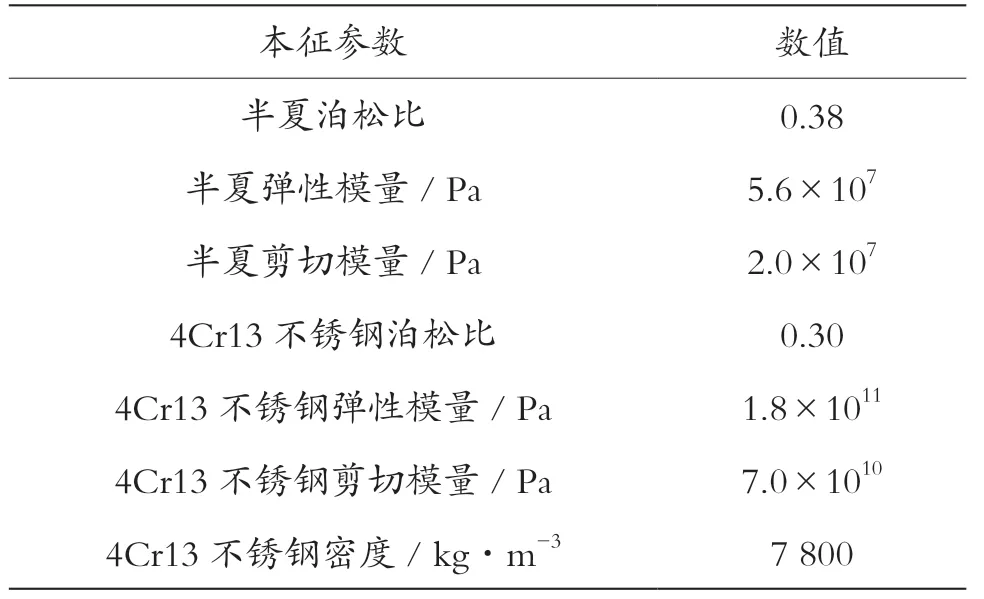
表1 试验材料本征参数

1.2 半夏的离散元模型

由于实际物体的形状并不规则，在离散元分析软件EDEM 中，通常采用多球聚合模型（Multisphere method，MSM）和粘结颗粒模型（Bonded particle method，BPM）构建离散元模型，离散元模型还原度越高，分析误差越小。MSM 通过若干不同大小的球形颗粒堆叠，建立不同形状的模型；BPM通过若干相同大小、互不重叠的球形颗粒，利用粘结键连接形成物体的离散元模型，互相粘结的球形颗粒半径越小，所需颗粒数量越多，离散元模型越逼近物体轮廓，所需的仿真时间越长。

由于半夏的外形较为简单、规则，本研究将其简化为下端钝圆的半球形，使用三维建模软件NX 12.0，以外形尺寸平均值建立半夏的三维模型，并导出为.msh 文件格式，最终获得半夏的轮廓网格模型（图2a）。将轮廓网格模型导入EDEM 软件，分别采用多球聚合模型和粘结颗粒模型构建半夏的离散元模型。模型如图2 所示，半夏的粘结颗粒模型（图2b）由82 300 颗半径均为0.15 mm 的球形颗粒组成，半夏的多球聚合模型（图2c）由11 颗不同半径的球形颗粒组成，综合考虑仿真试验的精度和效率，选择多球聚合模型所构建的离散元模型。

2 接触参数标定试验与结果讨论

半夏所需标定的接触参数有：半夏与不锈钢的碰撞恢复系数a、半夏与不锈钢的静摩擦系数b、半夏与不锈钢的滚动摩擦系数c；半夏间的碰撞恢复系数A，半夏间的静摩擦系数B和半夏间的滚动摩擦系数C。由于实际半夏的外形与简化的离散元模型存在差异，为减小标定的接触参数与实际接触参数的误差，本文将采用实际试验与离散元仿真试验结合的方式对半夏与不锈钢的接触参数进行标定。

2.1 半夏-不锈钢接触参数标定

2.1.1 半夏-不锈钢的碰撞恢复系数标定

如公式（4）所示，碰撞恢复系数定义为：碰撞后两物体相对分离速度与碰撞前相对接近速度之比，只与物体的材料有关，用于表征物体碰撞后恢复原形的能力。

假设物体1 在运动过程中只受重力影响，且物体2 碰撞前后速度均为0，则公式（4）可简化为

式中：

g——重力加速度，m/s2；

H——物体初始下落高度，mm；

h——物体最大弹起高度，mm。

根据公式（5），本文设计了图3 所示弹跳试验方案，规定半夏中心到不锈钢板的距离为半夏高度，将半夏从H=105 mm 处自由下落，与不锈钢板碰撞后弹起，采用高速相机拍摄全过程，并记录弹起的最大高度。试验重复5 次取平均值，确定半夏平均最大弹起高度为33.76 mm，碰撞恢复系数为0.567。将碰撞恢复系数a输入EDEM 软件，接触参数b、c、A、B、C均设置为0，进行5 次半夏下落碰撞仿真试验，得到平均最大弹起高度为35.12 mm，与实际高度的相对误差为4.03%，小于5%，表明标定的碰撞恢复系数准确性高。确定半夏-不锈钢的碰撞恢复系数为0.567。

2.1.2 半夏-不锈钢的静摩擦系数标定

采用斜面试验进行静摩擦系数的标定。试验原理如图4 所示，将半夏置于不锈钢板上表面，不锈钢板绕一棱线缓慢倾斜，当半夏开始滑移时立即停止转动，记录此时平板的倾斜角度y1。仿真试验中，为消除其他参数的影响，设置接触参数a=0.567，其余接触参数c、A、B、C均设置为0；通过最陡爬坡试验确定静摩擦系数的取值范围为0.35～0.70，步长取0.05，进行8 组仿真试验。实际试验采用分度值为0.01° 的数显角度尺测量倾斜角度；仿真试验中采用EDEM 量角器工具测量，每组试验重复5 次取平均值。得到不锈钢板的实际平均倾斜角度为34.72°，仿真试验结果如表2 所示。

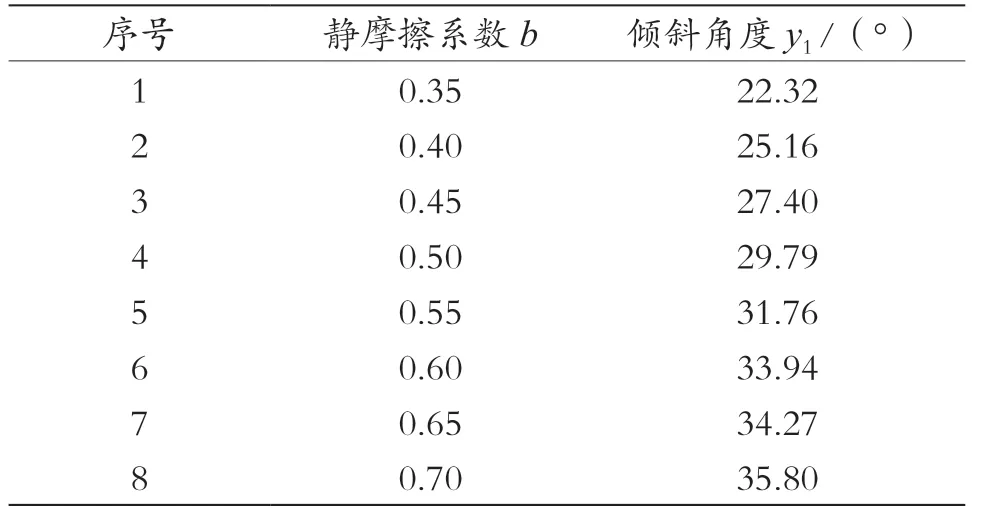
表2 静摩擦系数仿真试验方案与结果

图4 斜面试验

将表中数据采用Matlab 软件进行多项式拟合，拟合曲线如图5 所示，曲线函数为

图5 仿真试验静摩擦系数与平板倾斜角度拟合曲线

函数决定系数R2=0.996 5，趋近1，说明式（6）拟合精度高。将实际倾斜角度34.72°代入上式，解得b=0.649。将求解所得静摩擦系数输入EDEM 软件进行5 次重复试验取平均值，得到倾斜角度36.23°，与实际角度的相对误差为4.35%，小于5%，表明标定的静摩擦系数准确性高。通过上述过程，确定半夏-不锈钢的静摩擦系数为0.649。

2.1.3 半夏-不锈钢的滚动摩擦系数标定

半夏与不锈钢的滚动摩擦系数试验如图6 所示，将半夏从斜度为30°的斜坡顶端静止释放，并沿斜坡滚动至水平面，记录半夏在水平面上滚动的最远距离y2。在离散元仿真试验中，为消除其他参数的影响，设置接触参数a=0.567，b=0.649，其余接触参数A、B、C均设置为0；通过最陡爬坡试验确定滚动摩擦系数的取值范围为0.06～0.13，步长取0.01，进行8 组仿真试验。实际试验采用精度为0.02 mm 的游标卡尺进行测量；仿真试验中采用EDEM 长度测量工具，每组试验重复5 次取平均值。得到半夏的实际平均最远滚动距离为149.40 mm，仿真试验结果如表3 所示。

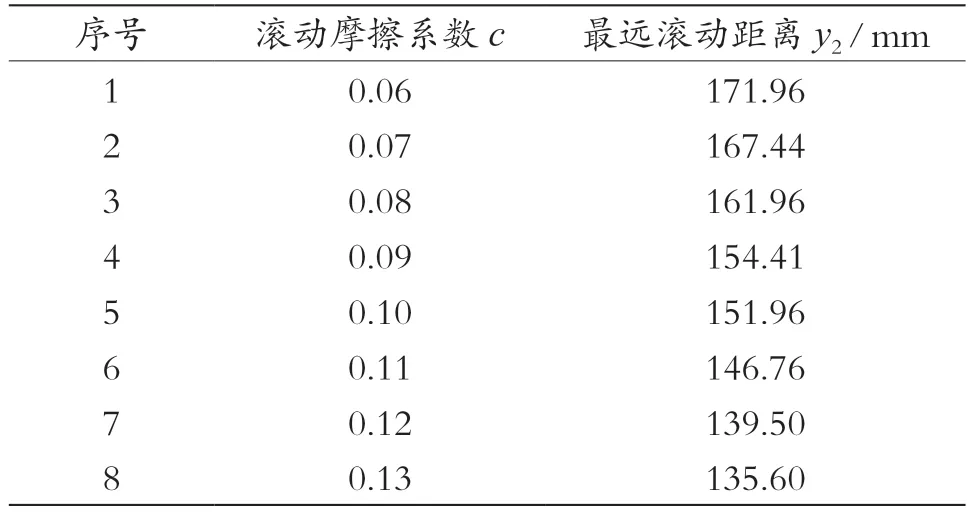
表3 滚动摩擦系数仿真试验方案及结果

图6 斜坡滚动试验

将表中数据采用Matlab 软件进行二次多项式拟合，拟合曲线如图7 所示，曲线函数为

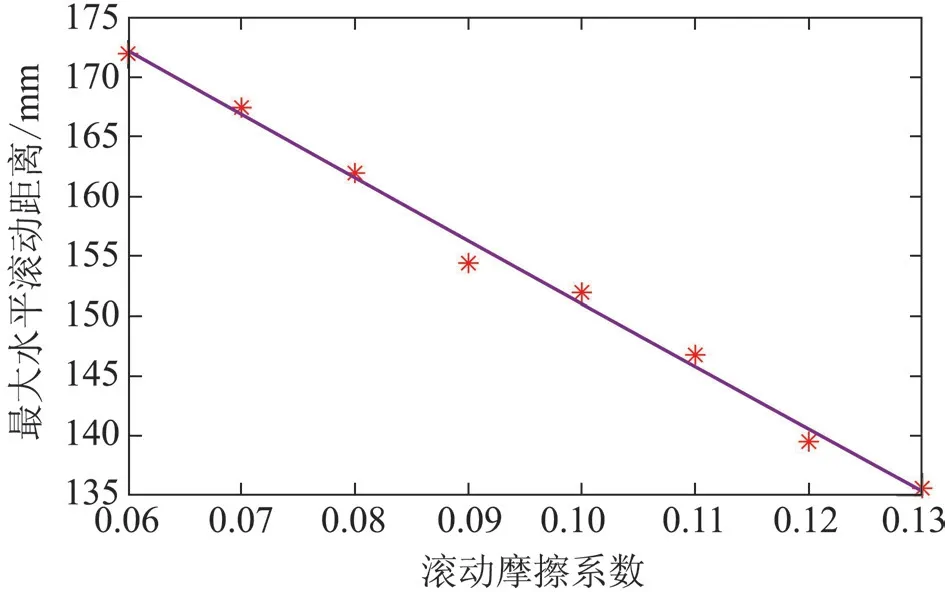
图7 仿真滚动摩擦系数与最大水平滚动距离拟合曲线

函数决定系数R2=0.994 1，趋近1，说明式（7）拟合精度高。将实际最远距离149.40 mm 代入上式，解得c=0.103。将求解所得静摩擦系数输入EDEM软件进行5 次重复试验取均值，得到最远滚动距离143.62 mm，与实际距离的相对误差为3.87%，小于5%，表明标定的滚动摩擦系数准确性高。通过上述过程，确定半夏-不锈钢的滚动摩擦系数为0.103。

2.2 半夏-半夏的接触参数标定

堆积角是大量颗粒自由下落堆积所形成锥体的自由表面与水平面的夹角，主要受颗粒表面形态、摩擦系数等因素影响。由于采用试验直接进行半夏间的接触参数标定存在困难，因此本文采用堆积试验，以仿真试验堆积角与实际试验堆积角的相对误差为指标间接求解半夏间的最佳接触参数组合。

2.2.1 堆积试验

如图8（a）所示，试验装置由带孔的有机玻璃箱和不锈钢圆盘组成。试验过程中，使用挡板将种箱孔封堵，再填入种箱体积2/3 左右的半夏，迅速抽离挡板使半夏从孔中自由下落，半夏在圆盘上堆积形成锥体，并采用相机拍摄锥体正视图。如图8（b）所示，锥体斜面与水平面的内角即为堆积角。重复试验结果表明锥体两侧的堆积角相对误差小于5%，本文选择锥体右侧进行堆积角测量。

图8 堆积试验

为降低测量误差，采用图像识别技术进行堆积角的测量。如图9 所示，依次对图像进行灰度处理、二值化、边缘检测和边缘直线拟合，并对堆积角角度进行测量。试验重复5 次，得到半夏的实际堆积角平均值为39.65°。

图9 图像处理

在仿真试验中，将试验装置的1∶1 三维模型导入EDEM 软件中，半夏离散元模型选择多球堆叠模型，颗粒接触模型选择Hertz-Mindlin 无滑移模型，设置接触参数a=0.567，b=0.649，c=0.103，仿真试验流程与实际试验相同。

2.2.2 仿真试验方案设计及试验结果

为构建准确的半夏间接触参数与堆积角相对误差的多元回归模型，本文基于三因素二次旋转正交组合试验方案设计仿真堆积试验。

如表4 所示，首先，依据最陡爬坡试验结果，分别以第3、4、5 组的碰撞恢复系数A、静摩擦系数B和滚动摩擦系数C为正交试验的-1、0 和1 水平因素。再采用Design-Expert 12 软件进行仿真试验因素编码和正交试验方案设计。仿真试验因素编码如表5 所示，仿真试验方案及结果如表6 所示，Y为仿真试验堆积角与实际堆积角的相对误差。

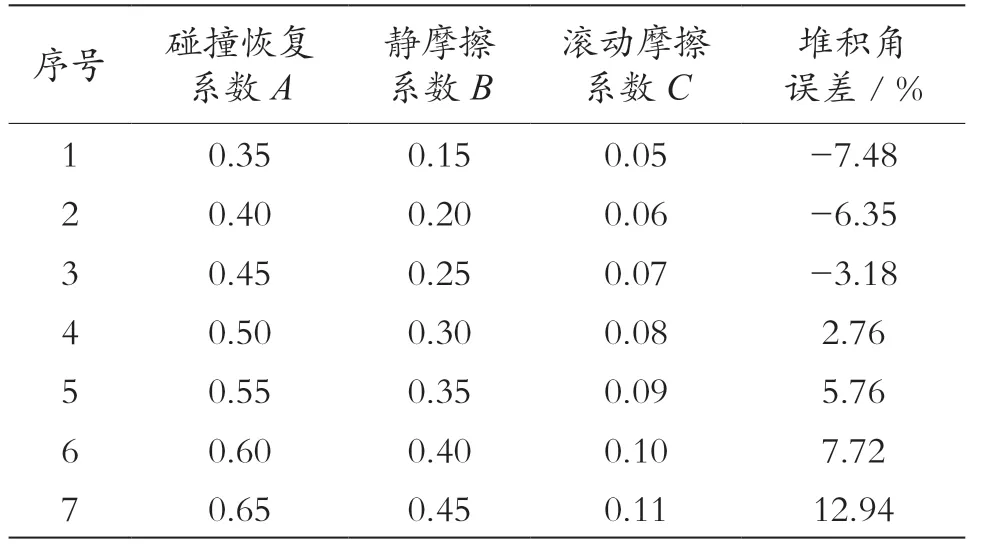
表4 最陡爬坡试验方案及结果

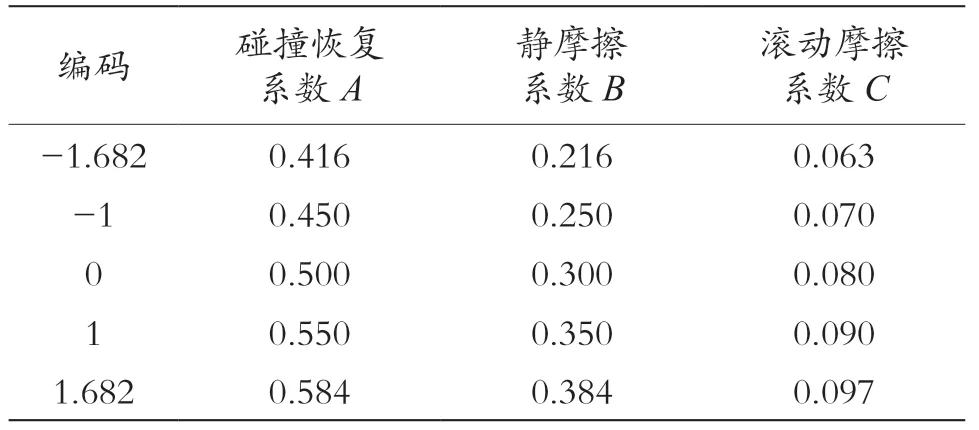
表5 仿真试验因素编码

表6 试验设计方案及结果

2.2.3 仿真试验结果分析

对仿真试验结果进行多元回归拟合，得到接触参数对堆积角相对误差的回归方程为

回归模型的方差分析结果如表7 所示，该模型的拟合度极其显著（P<0.000 1）。其中A、B、C、B2和C2的P值均小于0.01，表明相关因素对堆积角相对误差有显著影响。失拟项P值为0.081 6，不显著，表明无其他显著因素影响试验指标。方差分析结果验证了影响堆积角的主要因素为半夏间的碰撞恢复系数、静摩擦系数和滚动摩擦系数。

表7 回归模型方差分析

2.2.4 求解最优参数组合

以半夏间的碰撞恢复系数、静摩擦系数和滚动摩擦系数为优化对象，以堆积角相对误差最小为优化目标进行最优参数组合研究。目标函数和约束函数为

萤火虫算法（Firefly Algorithm,FA）是受自然界萤火虫发光行为启发的一种新型群智能优化算法[28]，该算法提出以下前提：①所有萤火虫不分性别，每只萤火虫会受比它更亮的萤火虫吸引；②吸引力与发光强度成正比；③个体的亮度由目标函数值决定。依据以上前提，定义萤火虫i在r=0 时的亮度为绝对亮度，即为Ii，则萤火虫i在萤火虫j处的相对亮度为

式中：

γ——光吸收系数；

rij——萤火虫i和j的距离。

由于发光强度与吸引力成比例，则萤火虫i对萤火虫j的吸引力表示为

式中：

β0——r=0 时的吸引力。

此时萤火虫j受萤火虫i的吸引，萤火虫j的位置发生变化，位置更新公式为

式中：

xi、xj——萤火虫i和j在空间中的位置；

k——迭代次数；

α——步长；

ε——高斯分布的随机向量。

萤火虫算法的基本流程如图10 所示。

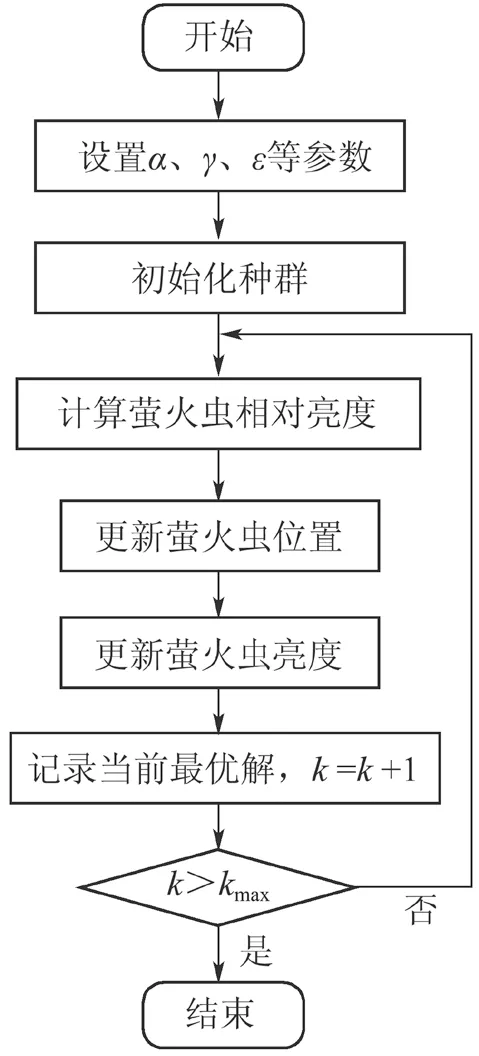
图10 萤火虫算法基本流程

相较于其他优化算法，萤火虫算法具有设置参数少，操作简便稳定的优点。由于每只萤火虫具有独立的感知和搜索能力，萤火虫算法不仅具有局部寻优能力，也能寻找全局最优解，因此，在求解连续的峰值函数时，萤火虫算法具有一定的优势。基于萤火虫算法的求解优势，本文采用萤火虫算法求解半夏间最优参数组合，得到半夏间最优接触参数组合为：碰撞恢复系数为0.584，静摩擦系数为0.293，滚动摩擦系数为0.084，此时堆积角的最小相对误差为0.58%。

3 试验验证

采用半夏的侧壁坍塌试验对上述试验标定的接触参数组合准确性进行分析验证。如图11 所示，在有机玻璃箱内填充2/3 体积的半夏，并迅速抽离右侧挡板，使半夏从容器右侧自然坍塌在不锈钢板上，待坍塌过程稳定后，采用相机拍摄半夏堆体的正视图。

图11 半夏侧壁坍塌试验

半夏堆体的斜面与水平面的夹角定义为休止角，休止角的测量方法与堆积角的测量方法相同，测量结果表明，实际休止角角度为27.08°。仿真试验中，将已标定的6 个接触参数输入EDEM 软件进行半夏的仿真坍塌试验，试验重复5 次。试验结果如表8所示，5 次试验的休止角相对误差均小于5%。综上，本文建立的半夏离散元模型及接触参数，在误差允许范围内可为半夏的离散元法仿真试验提供参考。

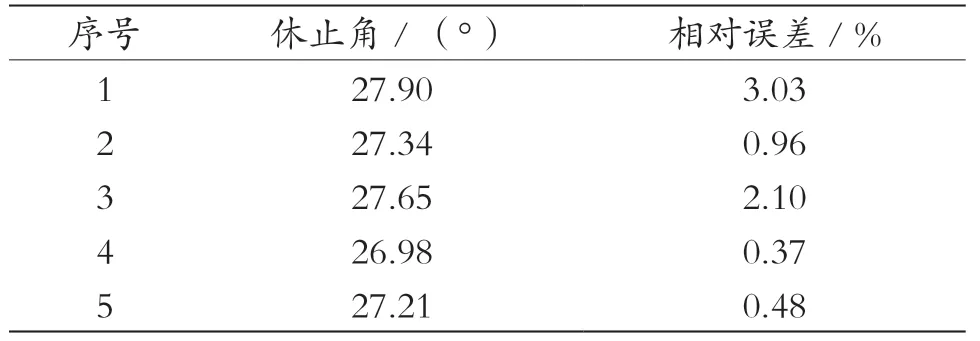
表8 侧壁坍塌试验验证结果

4 结论

1）基于多球聚合模型，建立半夏离散元模型。依据碰撞恢复系数定义，设计弹跳试验，标定半夏-不锈钢碰撞恢复系数为0.567。采用试验与仿真相结合的方法，通过斜面试验和斜坡滚动试验分别对半夏-不锈钢静摩擦系数、半夏-不锈钢滚动摩擦系数进行标定，建立目标参数与试验指标的数学模型，求解得半夏-不锈钢静摩擦系数为0.649，半夏-不锈钢滚动摩擦系数为0.103。

2）基于堆积试验，以实际试验和仿真试验的堆积角相对误差为指标，对半夏间的接触参数进行标定。以半夏间碰撞恢复系数、静摩擦系数和滚动摩擦系数为试验因素，设计了三因素二次旋转正交组合仿真试验方案，采用图像识别技术测量半夏堆积角。建立半夏间接触参数与堆积角相对误差的多元回归模型，并通过方差分析和响应面分析，验证了回归模型拟合的显著性（P<0.000 1）、表明了各因素及其交互作用对指标存在显著影响。

3）以堆积角相对误差最小为优化目标，采用萤火虫算法对半夏间接触参数与堆积角相对误差的多元回归模型进行求解，得到半夏间碰撞恢复系数为0.584，静摩擦系数为0.293，滚动摩擦系数为0.084。侧壁坍塌试验验证结果表明，5 次试验休止角相对误差均小于5%，因此该半夏离散元模型和接触参数可用于后续半夏的离散元法粉碎仿真试验。