改进灰狼算法的变电站巡检机器人路径规划

张 威,张鑫中,王丛佼,孙 兵

(1.上海电机学院 电气学院,上海 201306;2.上海海事大学 物流工程学院,上海 201306)

0 引言

变电站作为连接各级电网的枢纽,对站内设备进行定期巡检是保障电力系统安全的重要环节。变电站巡检机器人路径规划研究尤为重要,路径规划问题是利用智能优化算法实现智能巡检机器人的路径自主规划。以元启发式优化算法[1]为代表的智能优化算法,可以在搜索空间内快速随机地展开搜索,通过迭代搜索到的可行解,可以较小的计算代价寻找到全局的最优解。元启发代表的粒子群算法[2]、遗传算法[3]、蚁群算法[4]等已被用于机器人路径规划研究中。

近年来,灰狼算法[5](grey wolf optimizer,GWO)作为典型的仿生智能算法已应用于各类优化问题。虽然灰狼算法的收敛速度和求解精度优于遗传算法、差分进化和粒子群等算法[6],但由于其种群多样性差、后期收敛速度慢、易陷入局部最优,国内外学者进行了一系列改进算法研究。龙文等[7]将灰狼算法用于透镜成像学习策略的优化,避免了算法陷入局部优化;王敏等[8]在收敛因子上进行非线性的改进,平衡调整了算法的全局和局部的搜索能力;Gupta等[9]在全局优化方面进行算法改进测试;陈闯等[10]采用动态权重和概率扰动策略改进灰狼算法,以提高其搜索精度;李阳等[11]通过莱维飞行和随机游动策略改进灰狼算法,提升了算法的局部寻优能力以及寻优收敛速度;徐松金等[12]利用差分变异和随机收敛因子以提高灰狼算法的全局搜索能力和收敛精度;王正通等[13]采用局部参数优化和多样性种群方法对灰狼算法进行优化,并将其应用于火电机组的经济负荷调度。

针对灰狼算法在智能变电站上的路径规划,国内学者进行了一系列的研究。张承模等[14]利用机器人离线路径与传感技术研究了变电站路径规划问题;董翔宇等[15-16]将人工势场方法与双蚁群算法相结合,研究特高压机器人巡检机器人的路径规划问题,该方法降低了迭代次数,缩短了巡检路径,但运行效率有待进一步改进;童枭军等[17]融合了蚁群算法,基于A*算法,且引入碰撞惩罚机制,降低了智能机器人在变电站路径规划与自动避障中的边缘摩擦能力;游达章等[18]将灰狼算法与粒子群算法应用到机器人的路径规划中,以提升算法的收敛精度与稳定性;Chen等[19]研究了智能巡检机器人控制系统,并将其应用在变电站巡检中。

为进一步提高灰狼算法的效率,本研究中对传统灰狼算法进行优化,使用级数策略分配狼群权重,增大最优狼群的权值,改进其参数和位置更新公式;其次,对比分析不同自适应收敛函数的性能,选用最适合灰狼算法的收敛函数;最后,将改进后的灰狼算法用于智能变电站巡检机器人路径规划研究。

1 变电站栅格化建模

智能变电站巡检机器人全局路径规划研究中,首先针对某变电站进行二维栅格地图建模,继而根据变电站栅格地图进行路径规划。进行智能变电站栅格化建模时,将智能变电站中的建筑物和设备全部视为障碍处理,主要包括：主控大楼、主变压器、高压断路器、电容电抗设备、继电保护装置。

研究中应用二维栅格环境地图建模,针对智能变电站的特点,进行栅格化处理：① 确定障碍栅格。单元栅格数目由栅格分辨率与智能变电站实际环境的面积决定。② 二维地图模型表示。假设机器人工作区域为一个m×n的栅格坐标图,单位栅格长度设定为acm。地图建模区域大小为x×y。x、y计算公式[19]为

x=ceil(m/a)

(1)

y=ceil(m/a)

(2)

式中：ceil表示进一取整。

当栅格数值赋值为1时,表示此栅格为障碍物,用黑色表示;无障碍物时的赋值为0,用白色表示。在进行智能变电站巡检机器人路径规划研究中,将巡检机器人视为质点,忽略其运动模型。由于在进行变电站栅格化建模时,变电站单元栅格数目由栅格分辨率与智能变电站实际环境面积共同决定,本研究中以某220 kV变电站为对象,将实际5 m×5 m单元栅格化为1×1的栅格单元,图1为某变电站栅格化地图。如图1黑色栅格为智能变电站中的建筑物和电气设备,主要包括主控楼、主变压器、高压室、电容设备区、10 kV主变压器和220 kV设备区。设定每一栅格单元为1×1,巡检机器人路径长度采用欧式距离[20]描述,如式(3)所示。

(3)

式中：L为路径长度;np为路径点个数;(xi,yi)为坐标点坐标。

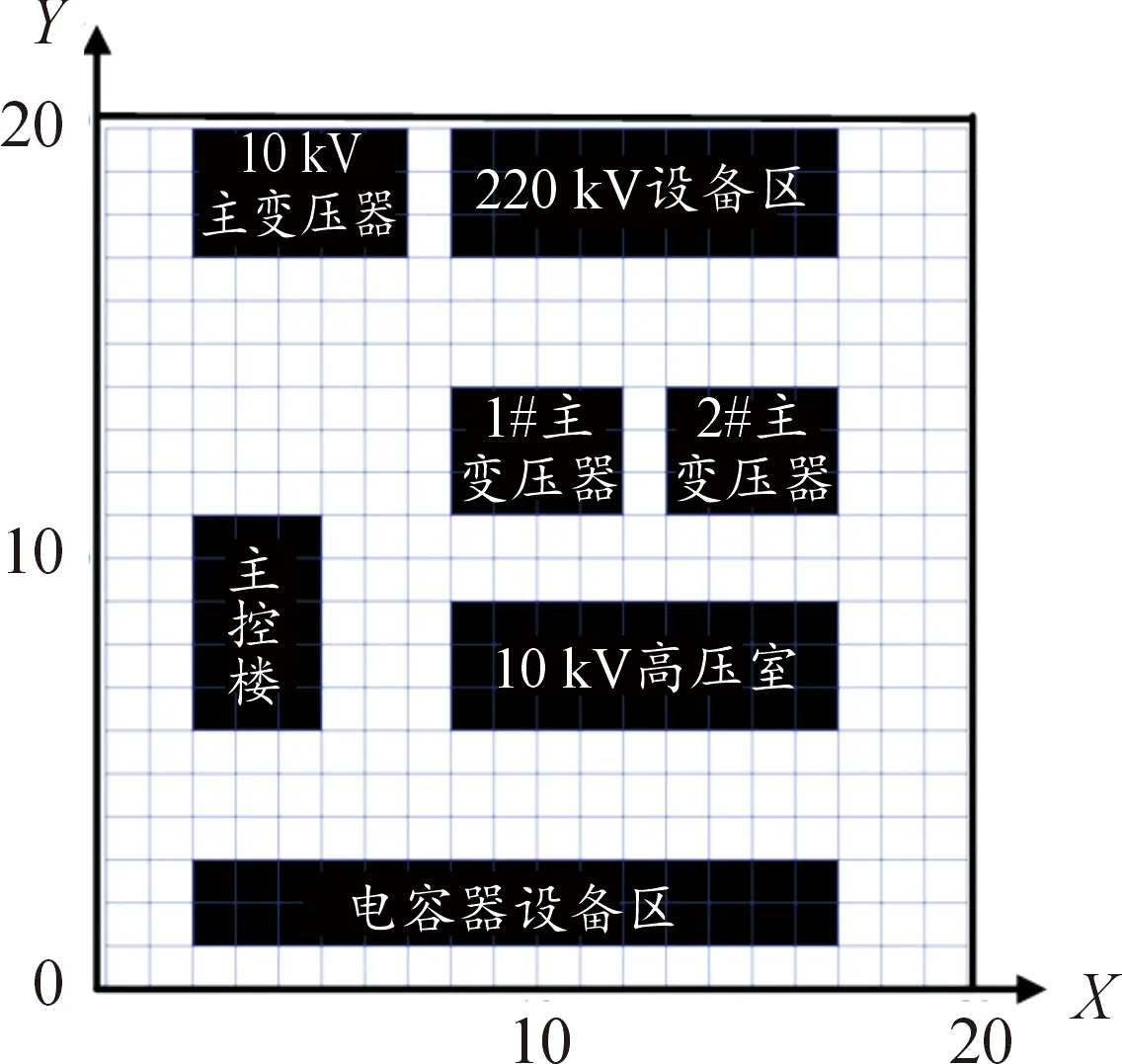
图1 某220 kV变电站栅格地图

2 基于改进灰狼算法的智能变电站巡检机器人路径规划

2.1 灰狼算法

灰狼算法是一个基于种群内部关系的自适应智能算法,为了狼群内部的种群平衡,4种类型的灰狼存在数量需要有适当的比例,相差过大,内部平衡被破坏。狼群中的每一只灰狼将会向着α、β、δ这3类位置最优的灰狼移动。图2为灰狼种群分布情况,依据灰狼捕猎的过程,将基础灰狼算法的数学模型分为3步,即追捕、包围、狩猎。

包围过程(寻找路径)的数学模型为

X(t+1)=Xp(t)-A·|C·Xp(t)-X(t)|

(4)

式中：X和Xp分别为灰狼和猎物的位置向量;t为当前的一个迭代次数;A和C算法系数向量,其定义分别如式(5)和(6)。

A=2a·r1-a

(5)

C=2a·r2

(6)

式中：r1与r2分别定义为[0,1]的一个随机向量;a为距离控制参数,其值随迭代次数的增加,从2线性减小到0[21]。

a(t)=2(1-tmax)

(7)

式中：tmax为最大迭代次数。

狩猎(更新位置)的数学模型为

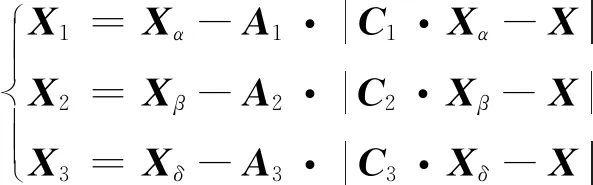
(8)

X1(t+1)=(X1(t)+X2(t)+X3(t))/3

(9)

式中：Xα、Xβ和Xδ分别为α、β和δ狼的位置向量。

图2 灰狼种群分布图

2.2 改进的灰狼算法

在智能变电站的建模环境下,应用原始的灰狼算法容易陷入局部最优,规划的路径过于单一,路径长度过长[20]。研究中,首先按照狼群中不同类型灰狼发挥作用的大小进行权重分配,增大α狼的权重,降低ω狼的权重;其次,根据自适应收敛函数的收敛速度选用合适的收敛函数,以提高灰狼算法的收敛效率。

2.2.1级数关系的权重分配

级数关系使各类灰狼的数量关系存在固定的比例关系,会起到优化灰狼种群的作用,原始灰狼算法中,A、C、X都涉及到权重分配问题,所以3个变量的公式都将得到改进。

设等比级数的通式为

bn=b1·qn-1

(10)

式中：b1为首项常数,q为公比,n为大于1的实数。

为了避免种群浪费,提高算法效率,首项与公比的设定不易过大,研究中首项b1∈[1,3],公比的设定q∈[2,5]。

基于等比级数参数A的改进公式为

(11)

灰狼算法利用系数向量A的一个取值范围来迫使灰狼与猎物分离,大于1表示远离目标去找寻下一个目标,对不同种类的灰狼设定不同的系数A,等比关系的确立使最优解的α狼能够率先寻找下一个解,可以提高寻优的效率和效果。

基于等比级数参数C改进公式为

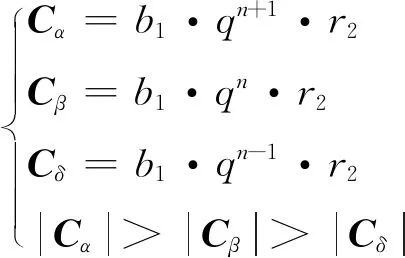
(12)

C表示灰狼所在的位置对猎物影响的随机权重,优化过程中避免陷入局部最优,系数向量C是[0,2]之间的随机值,|C|>1表示影响权重大,反之,表示影响权重小。

对参数C进行a到b的归一化处理。归一化处理的步骤为：

1) 找到样本数据Y的最小值及最大值。

2) 计算系数k

k=(b-a)/(Ymax-Ymin)

(13)

3) 得到归一化[a,b]区间的数据为

c=a+k(Ymin)

(14)

以Cα为例,归一化到[0,2]的范围上,首先样本Yα∈[0,b1·qn+1],计算的样本系数k=2/(b1·qn+1),得到归一化[0,2]区间的数据,公式表示为

Cα=kYα=(2/(b1·qn+1))Yα

(15)

同理,进行Cβ和Cδ的归一化。数据处理完成后,Yα的样本范围更大,α狼所在的位置对猎物影响的随机权重更大。基于等比级数位置更新改进公式为

(16)

2.2.2适配自适应收敛函数的选择

灰狼算法在实际的寻优过程中,要求其搜寻过程初始阶段收敛慢,扩大搜索空间,后期加快收敛,提升算法效率。传统灰狼算法中的线型收敛因子a搜索过程效果较差。改进目标为收敛因子a按照先慢收敛后加快的方向进行改进。常见的非线性收敛函数有指数函数、对数函数、三角函数等,对其进行改进。式(17)—(19)为改进的公式[8],式中lmax为最大迭代次数,l为当前的迭代次数。图3为函数收敛对比图。

a1=6.64lg[2-(lmax)2]

(17)

(18)

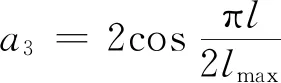
(19)

由图3所示的不同非线性收敛函数收敛过程可知,当自适应收敛函数a属于1到2时,为算法寻优阶段,需要拓宽搜索空间,这是为得到更多的可行解,收敛减速度慢。当a属于0到1时,为了提高算法效率,需要提高收敛速度,快速收敛到最优解。通过对比a1、a2和a3这3组不同的收敛函数,可知,收敛函数为a1时,收敛性最好。

2.2.3基于改进灰狼算法的智能变电站巡检机器人路径优化

基于灰狼算法的智能变电站巡检机器人路径优化,每只狼都代表了巡检机器人的一条路径,通过优化计算找出最优路径。基于改进灰狼算法路径规划的流程如图4所示。

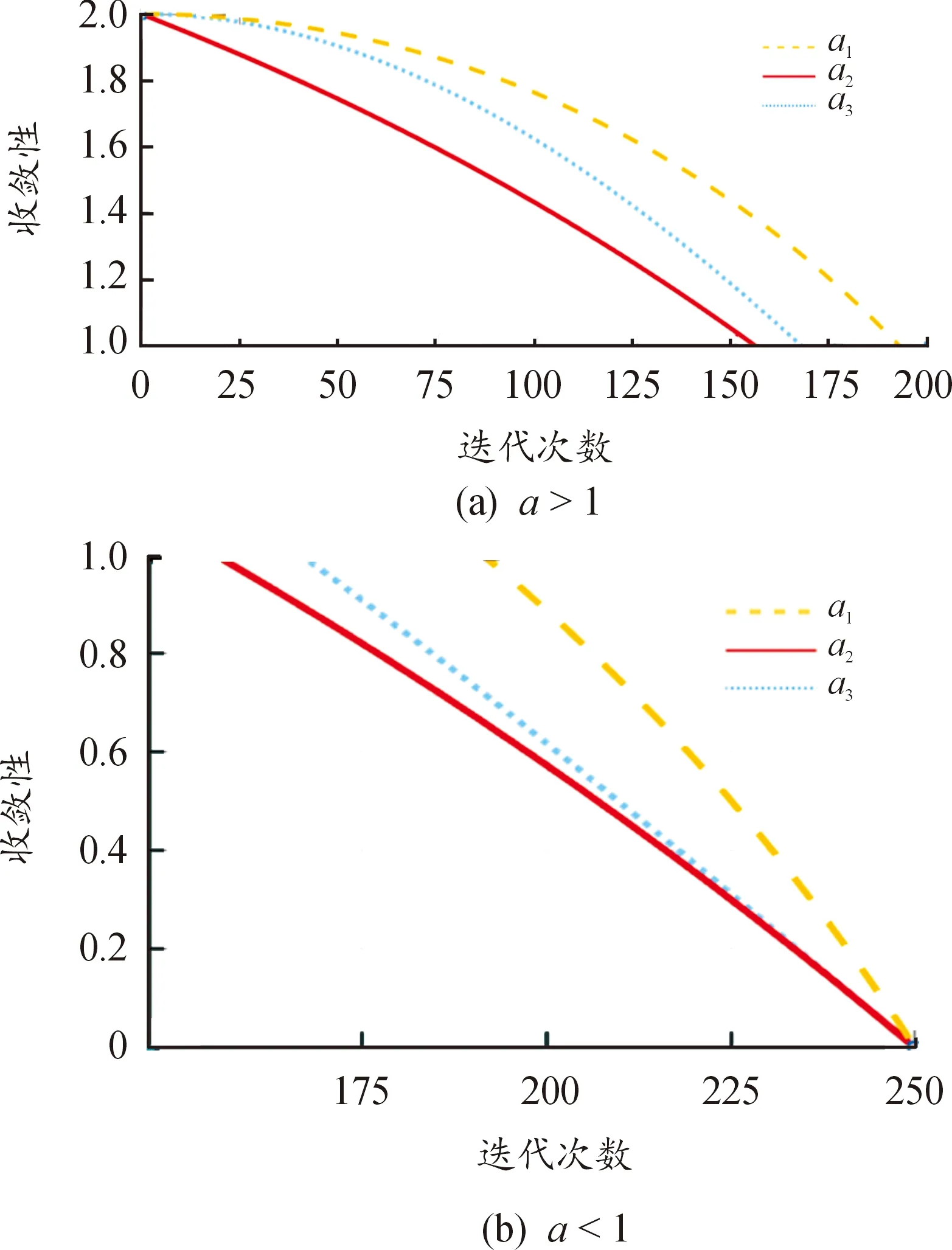
图3 不同非线性收敛函数对比

由图4可知,基于改进灰狼算法的智能变电站巡检机器人路径规划主要包括以下步骤：① 初始化改进灰狼算法的参数以及变电站栅格化地图数据;② 根据式(12)添加灰狼种群权重信息,以增加灰狼种群的多样性与差异性;③ 分别根据式(17)和式(8)改进灰狼算法收敛函数并初始化灰狼位置信息;④ 计算适应度函数,检验适应度函数是否达到期望值或者最大迭代次数,如果达到,则输出基于灰狼算法优化后的最优路径和路径距离,否则继续更新灰狼位置,计算灰狼算法的目标函数并返回步骤④,直至输出最优结果或达到最大迭代次数。

3 仿真与分析

为进一步分析不同智能优化算法在变电站巡检机器人路径规划中的性能,对比分析了基于蚁群算法、灰狼算法和改进后的灰狼算法,针对坐标为(7.5,13.5)任务点1、(17.5,5.5)任务点2、(0.5,19.5)任务点3、(19.5,0.5)任务点4之间的巡检效果。改进灰狼算法的智能变电站巡检机器人路径规划,基于Intel Core i5 2.5GHz处理器64位操作系统应用Matlab 2018软件进行改进灰狼算法的仿真分析。灰狼算法主要参数：种群个数N=50,最大迭代次数lmax=500,b1=3,q=4,c1=rand(0,1),c2=0.5+rand(0,1)。

3.1 基于蚁群算法和灰狼算法的路径规划

基于灰狼算法与蚁群算法的智能变电站巡检机器人路径优化结果如图5所示。

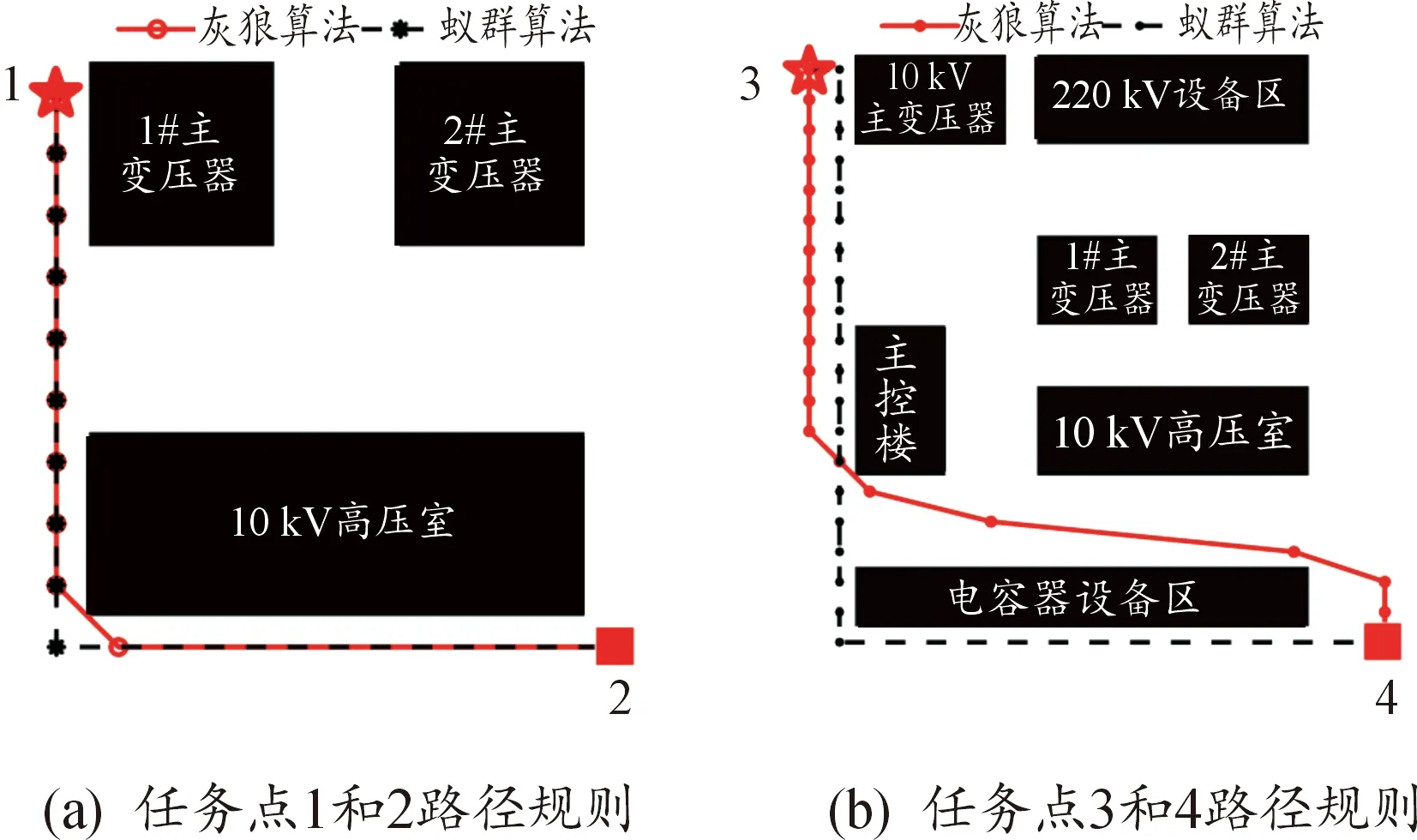
图5 基于蚁群算法与灰狼算法的路径优化结果

表1为2种优化算法下的路径规划结果。通过对比仿真结果,可知在进行任务点1和2之间,小范围路径规划时,基于蚁群算法和灰狼算法的路径分别为70和68,灰狼算法的平均运行时间为1.589 4 s,优于蚁群算法的4.152 1 s,平均运行时间缩短了61.72%;当进行任务点3和4之间,较大范围的路径寻优时,灰狼算法的优势明显,基于灰狼算法和蚁群算法的路径优化结果分别为310和348,灰狼算法的平均运行时间为1.592 2 s,较基于蚁群算法的5.551 4 s,运行速度提高了71.32%。

表1 基于灰狼算法和蚁群算法的路径规划结果

3.2 基于改进灰狼算法的智能变电站巡检机器人路径规划与仿真

通过对比蚁群算法和灰狼算法可知,灰狼算法在复杂的全局优化问题上优势明显,为进一步提高灰狼算法的性能,分别对灰狼算法的种群权重和收敛函数进行单独改进与混合改进,并分析基于这4种算法下,智能变电站巡检机器人在任务点3和4之间路径规划中的效果。表2为基于不同改进灰狼算法的路径规划参数。图6、7分别表示基于不同改进灰狼算法的路径规划收敛函数和路径规划图。

表2 基于不同改进灰狼算法的路径规划参数

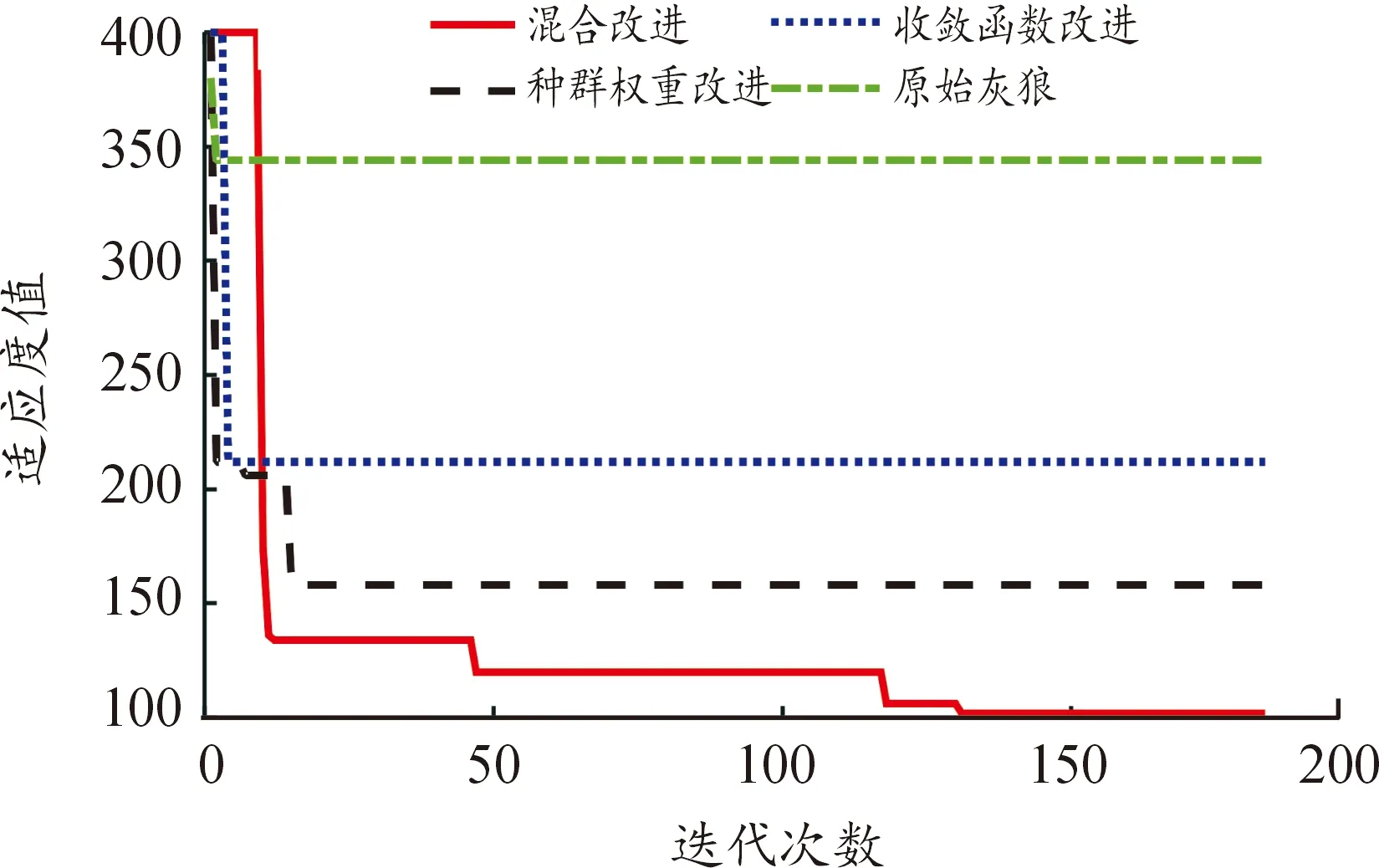
图6 基于不同改进灰狼算法的路径规划收敛函数曲线

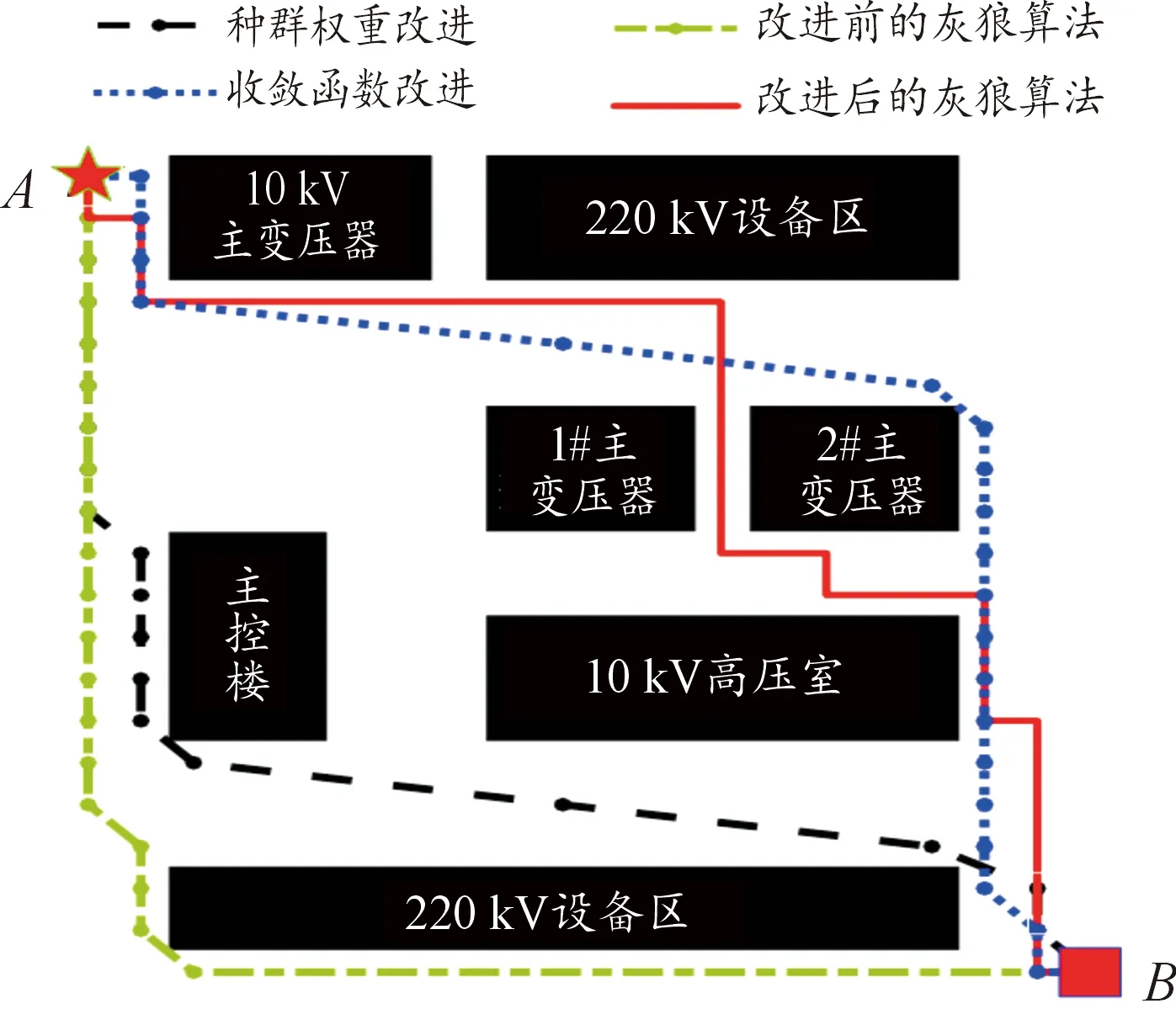
图7 基于改进灰狼算法的路径规划结果示意图

通过对比基于不同改进灰狼算法的路径规划结果可知,基于收敛函数和种群权重改进后的灰狼算法,使巡检路径由改进前330分别提高到222和168,平均运行时间由1.592 2 s分别缩短到1.296 0和1.263 6 s。基于收敛函数和种群权重这2个参数的混合改进算法,使路径缩短到104,较改进前的灰狼算法使路径缩短68.48%,平均运行时间将减少至0.893 9 s,运行速度提高了43.86%。基于收敛函数和种群权重这2个参数的混合改进灰狼算法在路径规划中取得了较好的效果。

4 结论

路径规划作为智能变电站巡检工作的重要内容,如何提高巡检效率尤为必要。通过对灰狼算法的改进优化,分析研究了基于改进灰狼算法在智能变电站巡检路径规划中的性能。研究结果表明,基于收敛函数和种群权重这2个参数的混合改进灰狼,在智能变电站路径规划中不仅提高了算法的运行效率,而且缩短了巡检路径,具有较好的路径规划性能。