基于向量平均投影测度的区间型组合预测模型

谢小军，马 虹，薛申芳，黄 鹏

（1.广州工商学院 通识教育学院，广州 510850；2.广东金融学院 金融数学与统计学院，广州 510521）

0 引言

在研究区间型组合预测方法时，如何确定组合权重系数，并且能够具有更好的精确预测值，一直是研究者所关注的核心问题。已有相关文献给出了一些区间型组合预测问题中求权重的不同方法，主要通过结合一些诱导算子构建某个准则下的最优模型。文献[1]结合诱导有序加权平均算子（IOWA）构建了区间组合预测模型。文献[2]引入诱导广义有序加权对数平均算子（IGOWLA），建立以误差平方和为最优准则的组合预测模型。文献[3]以灰色趋势关联度为最优准则，并引入广义诱导有序加权平均算子（GIOWA）构建了组合模型。文献[4]引入诱导有序加权几何平均算子（IOWGA），以用区间中心和区间半径预测误差绝对值之和最小为准则建立了组合预测模型。文献[5]引入连续有序加权平均算子（COWA）,以相关系数为最优准则建立了优化组合预测模型。文献[6]通过引入诱导连续有序加权平均算子（ICOWA），以预测有效度为最优准则构建区间组合预测模型。文献[7]引入诱导有序加权几何平均算子（IOWGA），以三角模糊数左右区间的相似度作为最优准则构建最优化模型。文献[8]通过结合连续区间的广义有序加权多重平均算子（C-GOWMA）和诱导有序加权平均算子（IOWA），建立以指数支撑度为最优准则的区间型组合预测模型。文献[9]引入诱导广义有序加权多重平均算子（IGOWMA）,以广义向量夹角余弦为最优化准则构建区间型组合预测模型。文献[10]通过信息熵的不同形式，给出了三种可行的研究方法来确定区间型组合预测权重。鉴于向量投影是一个综合性测度，既能反映两个向量指标对象之间的距离，又能反映他们之间的夹角，因此本文将已有研究者提出的一些向量投影测度公式引入，并在此基础上提出了一种新的投影测度公式。对这些投影测度公式加以推广用来描述两个区间数时间序列的接近程度，以组合预测区间数序列与实际区间数时间序列平均标准化投影测度为最优化准则，构建了四个不同平均标准化投影测度的全新区间型组合预测模型；并通过实例分析，将预测结果与已有研究文献中的区间型组合预测优化模型进行对比。

1 相关概念

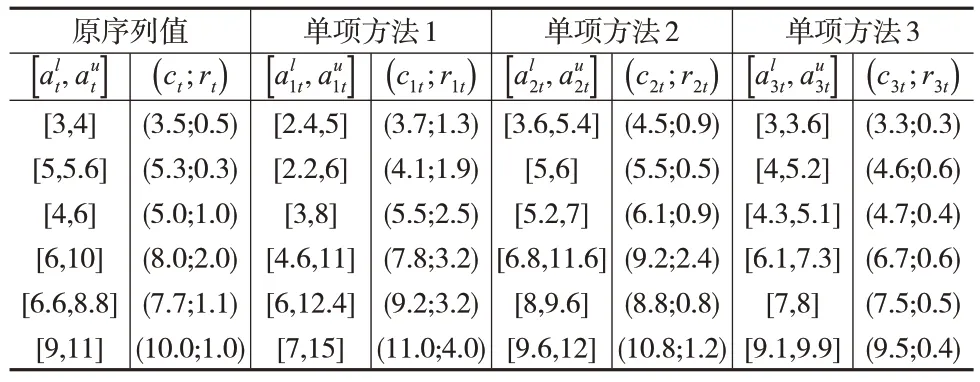
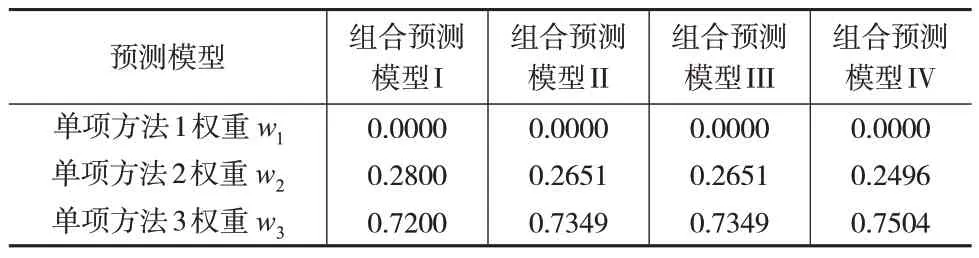
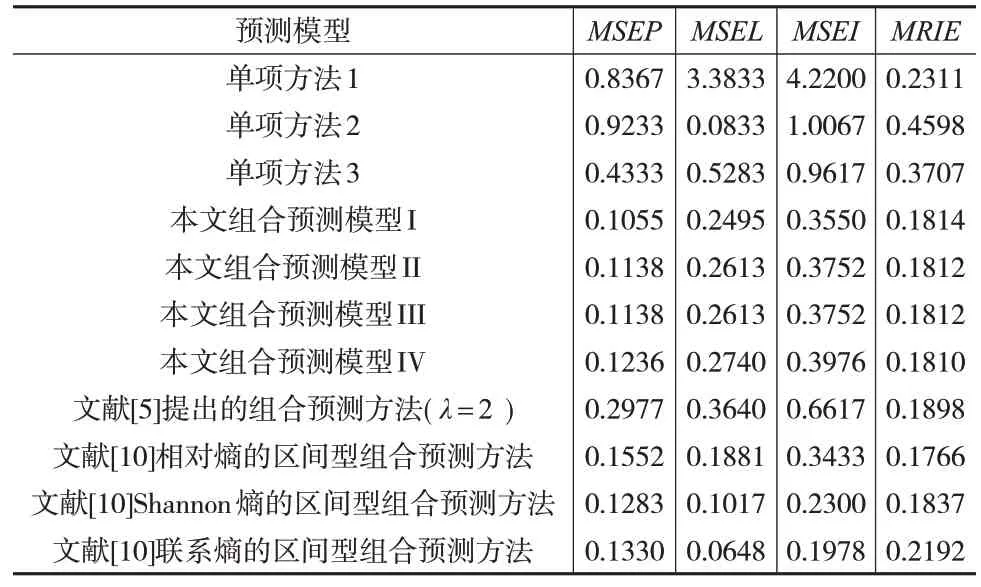
定义1[1]：设a=[al,au]，其中，al,au∊R，且满足0

因此文献[12]给出了如下公式：

该文献提出以下标准化投影测度公式：

文献[13]给出了如下标准化投影公式：

文献[14]给出了如下标准化投影公式：

定义3：设任意两个区间数a=[al,au] 和b=[bl,bu]，其中0

其中，RPb(a)=(ab)/b2，ab=albl+aubu，a2=(al)2+(au)2，b2=(bl)2+(bu)2，可知NPb(a)越大，表示区间数a和区间数b越接近。

2 模型的建立

（2）基于向量标准化投影的区间型组合预测模型II

（3）基于向量标准化投影的区间型组合预测模型III

（4）基于向量标准化投影的区间型组合预测模型IV

3 实例分析

为了说明本文提出的四种模型的有效性，并和已有文献的预测方法的结果作对比研究，本文选取文献[1,10]中实例分析中的数据作为基础数据，具体数据见表1。

表1 原序列值和各单项预测序列值

将表1 数据利用式（10）计算m种单项预测方法在第t时刻的组合预测区间数序列，分别用式（11）至式（14）计算组合预测区间数序列与实际区间数时间序列的平均标准化投影NPX()，然后分别代入建立的四个优化模型中，利用Lingo11计算求得对应的最优权重系数，见表2。

表2 组合模型的最优权重系数

通过求解得到的表2 所建立的四种模型的最优权重系数，可以进一步计算得到组合预测区间数序列以及其等价表示，结果见表3。

为了对本文提出的方法的预测结果作出客观评价，验证基于向量投影测度的四种区间型组合预测模型的有效性，以区间数序列的绝对误差指标（MSEP、MSEL、MSEI）和区间数序列的相对误差指标（MRIE）作为评价指标对预测效果进行评价，计算公式如下：

根据表3 中实际值区间数和四种基于向量平均标准化投影的区间型组合预测值区间数及其等价表示，依据上述区间数序列的绝对误差和区间数序列的相对误差公式对各预测方法的效果评价指标值进行计算，计算结果见下页表4。

表4 预测效果评价指标值

从表4中各预测方法的预测效果评价误差指标来看：

（1）本文提出的基于向量投影测度的四种区间型组合预测模型要优于所有单项预测方法。四种基于向量投影测度的区间型组合预测模型的四个误差指标MSEP、MSEL、MSEI、MRIE在数值上都明显小于各单项预测方法相应的误差指标。

（2）四种基于向量投影测度的区间型组合预测模型也优越于文献[1]中提出的区间型组合预测方法。在四种基于向量投影测度的区间型组合预测模型中，MSEP、MSEL、MSEI、MRIE在数值上都明显小于文献[1]中所提预测方法相应的误差指标值。

（3）四种基于向量投影测度的区间型组合预测模型与文献[10]中提出的三种基于熵值的区间型组合预测方法效果相当。在四种基于向量投影测度的区间型组合预测模型中，MSEP在数值上都小于文献[10]中基于熵值的三种区间型组合预测方法；四种组合预测模型的MSEL、MSEI在数值上都大于文献[10]中基于熵值的三种区间型组合预测方法；四种组合预测模型的MRIE在数值上小于文献[10]中提出的Shannon 熵的区间型组合预测方法和联系熵的区间型组合预测方法，略大于文献[10]中提出的相对熵的区间型组合预测方法。

（4）在四种基于向量投影测度的区间型组合预测模型中，组合预测模型I在绝对误差指标MSEP、MSEL、MSEI上更加优越，组合预测模型IV在相对误差指标MRIE上更加优越，而组合预测模型II和组合预测模型III效果一样。

综上可知，本文提出的四种基于向量投影测度的区间型组合预测模型能有效减少预测误差，提高单项预测方法的预测精度，是一种非劣性区间型组合预测模型。

4 结论

本文对区间型组合预测模型进行研究，区间型组合预测模型的核心问题是如何确定各单项预测方法的权重。鉴于向量投影具有更好的综合测度，它可以同时反映两个向量指标之间的距离和夹角，因此，本文通过引入向量投影测度公式，并在此基础上提出了一种新的投影测度公式。通过对向量投影测度公式加以推广用来描述两个区间数时间序列的接近程度，以平均标准化投影测度为最优化准则，构建了四个不同投影测度的全新区间型组合预测模型。并通过实例分析验证了所构建的组合预测模型是一类有效的区间型组合预测模型。