基于局部集合和差分进化的过抽样方法

罗少甫

（重庆航天职业技术学院 智能信息学院，重庆 400021）

0 引言

不平衡数据集的类别呈偏态分布[1]。在不平衡数据集中，会存在一个样本数量较少的类，学者们通常把这个类称为少数类。同时，学者们把具有较多样本数量的类称为多数类。由于不平衡数据集的偏态分布，因此从不平衡数据集上学习一个有效的分类器（即不平衡分类）是一个挑战[2]。在不平衡分类中，尽管分类模型能取得较高的分类正确率，但是他们难以正确地分类少数类。相比于多数类，少数类更具有实际意义。

欠抽样方法和过抽样方法能够改进不平衡分类[3—8]。欠抽样方法会去除多数类中的冗余样本，直到样本的类别分布平衡。过抽样方法生成少数类的合成样本去扩充少数类。SMOTE（Synthetic Minority Over-sampling Technique）[9]是最流行的过抽样方法。它用少数类样本的k近邻[10]插值结果去生成合成样本；然后，用生成的合成样本去扩充少数类。到目前为止，SMOTE 具有巨大的实际应用价值和许多改进算法。例如，Boderline-SMOTE[11]、ADASYN[12]、RSMOTE[13]、Adaptive-SMOTE[14]等。

研究发现，大多数过抽样方法容易生成噪声[9,11—15]。这是因为他们用噪声或（和）不安全的边界样本去生成合成样本。最近，基于噪声过滤的过抽样方法能解决噪声生成问题。SMOTE-TL[16]、SMOTE-ENN[16]和SMOTE-IPF[17]是基于噪声过滤的过抽样方法。SMOTE-TL 用托梅克链接（Tome Link，TL）去移除合成样本和原始数据中的噪声。SMOTE-ENN 用k 近邻分类器去识别和过滤噪声。SMOTE-IPF 用一个迭代的随机森林分类器来去除合成样本和原始数据中的噪声。尽管大量的实验[15—17]证明了基于噪声过滤的过抽样方法的有效性，但是他们仍然有以下不足：（1）在大多数基于噪声过滤的过抽样方法（如SMOTE-TL、SMOTE-ENN 和SMOTE-IPF）中，噪声侦察技术依赖于参数，这导致算法表现不稳定和应用困难。（2）全部的基于噪声过滤的过抽样方法均用k 近邻的插值结果去生成合成样本。因此，生成合成样本的过程依赖于近邻参数k。（3）基于噪声过滤的过抽样方法均会移除过多的少数类样本。这是因为基于噪声过滤的过抽样方法用有监督分类器（如TL[15]、k 近邻[16]和随机森林[17]）作为噪声过滤器。由于不平衡数据的影响（没有考虑不平衡数据的特性），这些有监督分类器容易错误地预测少数类样本。从而，噪声过滤器会错误地识别大量的少数类样本为噪声；并且，他们会直接移除可疑的噪声，而不是更正或优化，这最终会导致信息损失。

为了克服噪声生成和上述基于噪声过滤的过抽样方法的缺陷，本文提出了一种基于局部集合和差分进化的过抽样方法（Oversampling Method based on Local Sets and Differential Evolution，OMLSDE）。首先，该方法计算每个样本的局部集合[18]；其次，该方法用局部集合和不平衡比去发现更多的多数类噪声，并且保留更多的少数类样本，这提高了少数类的泛化性；然后，该方法用差分进化[19]去优化可疑的噪声（迭代地改变噪声的属性或位置），而不是直接移除他们；最后，该方法用局部集合内的随机样本去生成少数类的合成样本。

1 理论基础

设训练集X={x1,x2,…,xnmin,xnmin+1,…,xn},X∊RD。其中，D为属性的个数，n为训练集样本的个数。设少数类样本集合Smin={x1,x2,…,xnmin}，其中，nmin为少数类样本的个数。设多数类样本集合Smaj={xnmin+1,xnmin+2,…,xn}。其中，nmaj为多数类样本的个数，nmaj=nnmin。

1.1 局部集合

Brighton 和Mellish（2002）[19]提出了局部集合（Local Sets，LS）的概念。局部集合受敌最近邻（Nearest Enemy，NE）的启发。一个样本xi的局部集合包含一些特定的样本，这些特定样本到xi的距离小于xi到xi的敌最近邻的距离。由于概念上的优越性和简单性，实例约简和多标签学习已经用到了局部集合的概念[8]。本文把NN(xi)定义为样本xi的最近邻，并定义敌最近邻如下：

定义1（敌最近邻）：一个样本xi的敌最近邻是离xi最近的不同类的样本。本文把样本xi的敌最近邻记为NE(xi)。

在式（1）中，数据集X包含少数类（Smin）和多数类（Smaj）。

基于敌最近邻的概念，本文定义局部集合如下：

定义2（局部集合）：一个样本xi的局部集合（Local Set，LS）包含一些特定的样本xj。这些特定样本xj到xi的距离小于xi到其敌最近邻NE(xi)的距离。

在式（2）中，dist(xi,xj)或dist(xi,NE(xi))代表两个样本的欧氏距离。

进一步，本文定义局部集合基数如下：

定义3（局部集合基数）：一个样本xi的局部集合基数（Local Set Cardinality，LSC）是局部集合LS(xi)中的样本个数。

在式（3）中，|·|代表数量。

图1 用一个人工例子去可视化局部集合。在图1 中，圆圈代表少数类，三角形代表多数类。并且，部分样本指向它的敌最近邻。从图1 可以发现，NE(A)=F，NE(C)=G，NE(B)=H，NE(E)=I，LS(A)={A,D}，LS(B)={A,B,C,D}，LS(C)={C}，LS(E)={E}。局部集合有如下特性：

（1）一个局部集合中的样本有相同的类标号。

（2）如果样本xi更接近边界，则这个样本xi有更小的LSC(xi)值。在图1 中，LSC(A)=2，LSC(B)=4 和LSC(C)=1。样本C更靠近边界。

（3）如果越多的局部集合包含样本xi，则样本xi越安全。在图1 中，噪声样本E位于LS(E)中，更安全的样本C位于LS(C)和LS(B)中，更安全的样本D位于LS(A)和LS(B)中。

（4）如果越多的样本xj视样本xi为敌最近邻，则样本xi越靠近其他类别。在图1中，大量的样本视噪声样本E和边界样本C为敌最近邻

2 基于基本集合和差分进化的过抽样方法

OMLSDE 的目标是防止噪声生成和解决基于噪声过滤的过抽样方法的缺陷，即：（1）噪声侦察技术依赖于参数；（2）合成样本的过程依赖于参数k(c)，他们会移除大量的少数类样本，造成信息损失。

图2 用一个人工例子来展示OMLSDE 的主要思想。首先，本文用局部集合和不平衡比去发现可疑的噪声（见图2（b））。在图2（b）中，本文用五角星标出被识别的可疑的噪声样本。其次，本文用差分进化去优化可疑的噪声（即改变噪声的位置或属性），而不是直接删除他们，这防止了大量样本信息的丢失（见图2（b）和图2（c），OMLSDE优化了可疑噪声的属性或位置）。再次，本文用局部集合内的随机样本去生成合成的少数类样本（见图2（d））。最后，本文用这些合成的少数类样本来扩充少数类样本集。因此，本文能用这个优化的训练集去改进传统的分类器。

图2 用一个人工例子去说明OMLSDE

2.1 基于局部集合和不平衡比的噪声侦察技术

现有的基于噪声过滤的过抽样方法[15—17]依赖于噪声侦察技术的参数。而且，由于没有考虑不平衡数据的特性，他们会误识别大量的少数类样本。在这个部分，用局部集合和不平衡比去侦察可疑的噪声。

由前文的分析可知，如果越多的局部集合包含样本xi，则样本xi就越安全；如果越多的样本xj视样本xi为敌最近邻，则样本xi就越靠近其他类别。因此，本文定义样本xi的有用性和有害性如下：

定义4（样本xi的有用性）：样本xi的有用性（Useful⁃nes（sxi））是包含样本xi的局部集合的个数。

定义5（样本xi的有害性）：样本xi的有害性（Harm⁃fulness（x）i）是把样本xi视为敌最近邻的样本个数。

在式（4）和式（5）中，样本xi的有用性Usefulnes（sx）i代表样本xi的安全性。样本xi的有用害Harmfulness（x）i代表样本xi的反常性。基于这个理解，本文用如下公式去侦察可疑噪声。

在式（6）中，IR代表不平衡比，IR的值等于nmaj除以nmin；nmaj代表多数类样本的个数，nmin代表少数类样本的个数。

在不平衡数据中，当本文计算有用性和有害性的时候，少数类样本的有用性相比于它的有害性会较小。这是因为多数类的样本数目（产生有害性）大于少数类的样本数目（产生有用性）。同理，多数类样本的有害性相比于它的有用性会较小。通过考虑不平衡比IR，式（6）能发现更多的多数类样本的噪声。而且，式（6）也能保留更多的少数类样本，从而提高少数类的泛化性。

图2（b）展示了用式（6）去发现可疑噪声的结果。从图2 中可以发现，算法能发现更多的多数类噪声，并且保留更多的少数类样本。并且，式（6）不需要任何参数。

2.2 用差分进化优化可疑噪声

大多数基于噪声过滤的过抽样方法[15—17]会直接去除可疑噪声，这会导致信息损失。在这个部分，本文用差分进化去优化可疑噪声的属性（位置）。设可疑噪声集合和安全样本集合分别为SuspiciousSet和SafeSet，X=SuspiciousSet∪SafeSet。

差分进化[19]是一个迭代的优化算法。它包括初始步骤、变异步骤、交叉步骤和选择步骤。

在初始步骤中，本文把每一个可疑噪声xi∊SuspiciousSet视为一个目标向量ti,g。设目标向量集合为Tg={t1,g,…,ti,g,…}，其中：

在式（7）中，g代表迭代次数，设Gmax为最大迭代次数，则g∊{1,2,…,Gmax}；d代表第d个属性，d∊{1,2,…,D}；ωi代表目标向量ti,g的类标号。

变异步骤为每一个目标向量ti,g生成一个变异向量vi,g。本文使用DE/Rand/1[19]策略去生成变异向量vi,g。设变异向量集合为Vg={v1,g,…,vi,g,…}，其中：

在式（8）中，本文从安全样本集合SafeSet中随机地选取3 个样本xr1、xr2和xr3；Fi是用于控制变异程度的缩放因子。

在交叉步骤中，本文会用目标向量ti,g和变异向量vi,g去生成一个测试向量ui,g。本文用DE/CurrentToRand/1策略去生成测试向量ui,g。设测试向量集合为Ug={u1,g,…,ui,g,…}，其中：

在式（9）中，K是0到1之间的随机值。在式（7）至式（9）中，差分进化用目标向量ti,g和变异向量vi,g的线性组合来生成测试向量ui,g。值得注意的是，测试向量ui,g和目标向量ti,g具有相同的类别ωi。

在选择步骤中，本文用式（10）去决定是否用测试向量集合Ug更新目标向量集合Tg+1。

在式（10）中，C代表一个特定的分类器。在实验中，本文用最近邻分类器[10]作为这个特定的分类器C。本文用安全样本集合SafeSet去训练分类器C。accuracy(C,Ug)代表分类器C在Ug上的分类正确率，accuracy(C,Tg)同理。如果分类器C在Ug上的分类正确率大于或等于分类器C在Tg上的分类正确率，那么本文就用Ug更新目标向量集合Tg+1。差分进化的停止条件是accuracy(C,Tg)等于1。换言之，当分类器C能正确分类所有的（被优化后的）可疑噪声时，差分进化停止。

差分进化算法有一个参数Fi。本文用文献[19]的方法去设置参数Fi。

其中，rand2和rand3是0到1之间的随机值。文献[19]建议，SFGSS=8，SFHC=20，Fl=0.1，Fu=0.9，τ1=0.1，τ2=0.03，τ3=0.07。

本文用差分进化算法去迭代地改变目标向量（可疑噪声）的属性和位置，直到一个特定的分类器C能正确地分类所有的目标向量（可疑噪声）。如图2（b）和图2（c）所示，当差分进化停止的时候，本文能将所有的可疑噪声优化到正确的位置，从而防止信息损失，也能改进其分布。差分进化的伪代码如下页表1所示。

表1 差分进化算法（DE）

设分类器C的时间复杂度为O(C)，可疑的噪声集合SuspiciousSet的样本数为NSE。如文献[19]推导，差分进化的时间复杂度为O(Gmax×NSE×C)。

2.3 提出算法

OMLSDE 算法有两个参数，即参数N和参数Fi。参数N指的是，基于每个少数类样本需要生成的合成样本数目[9]。参数Fi用于调整差分进化。

下页表2中，算法的第1至第3步用于搜索局部集合。算法的第4 和第5 步用局部集合和不平衡比发现可疑噪声。算法的第6和第7步用差分进化去优化可疑噪声。算法的第8 至第19 步用每个少数类样本和其局部集合中的随机样本去产生合成的少数类样本（见图2（d））。在第8和第9步中，本文仅把局部集合基数大于1的样本作为基样本去生成合成样本。在第14步中，用rand（0，1）产生0到1的随机值。

表2 基于局部集合和差分进化的过抽样方法（OMLSDE）

由于使用kd 树，因此第2 步的时间复杂度是O(nlogn)。第3至第5步的时间复杂度是O(n)。第6和第7步（差分进化）的时间复杂度是O(Gmax×NSE×C)。第8至第19步的时间复杂度是O(N×D×nmin)。这是因为它与少数类样本数目nimn、参数N和属性D有关。因此，OMLSDE 算法的时间复杂度是O(Gmax×NSE×C)+O(N×D×nmin)。

3 实验

3.1 实验设置

本文从UCI数据集（http：//archive.ics.uci.edu/ml/datasets.php）上选出15个实验所需的真实数据集。表3给出了这15 个真实数据集的具体信息。这些信息包括样本数、属性数、少数类样本数、多数类样本数、不平衡比和数据集缩写。在表3 中，如果一个真实数据集是二类数据集，本文把样本数量较少的类作为少数类，同时把样本数量较多的类作为多数类；如果一个真实数据集是多类数据集，本文选择数量最少的类作为少数类，并将其他类合并为一个大的多数类。

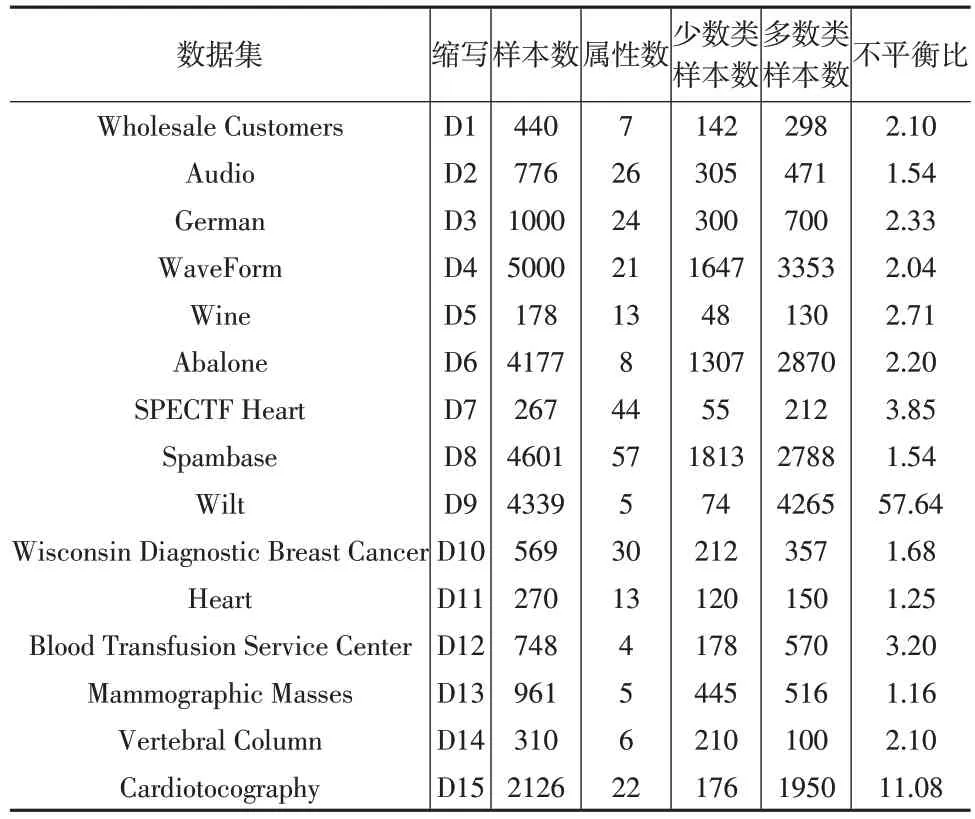
表3 实验的数据集

本文用十折交叉验证把每个数据集划分为测试集和训练集。十折交叉验证会重复运行实验10次。在每一次实验中，十折交叉验证把每个数据集划分为10等份，训练集包含9份，测试集包含1份。

在本文的实验中，本文把少数类看作正例，把多数类看作负例。另外，本文选取AUC、F-measure 和G-mean 作为评价指标。AUC 值越高，代表算法的总体性能越好。F-measure 线性地结合了召回率Recall 和精确度Precision。F-measure 值越高，代表算法能把正例分类得越准确。G-mean 的公式包含了正例的正确率和负例的正确率。G-mean在保持正、负例分类精度平衡的情况下，最大化这两类的精度。假定对负例的分类精度很高，而对正例的分类精度很低，则会导致低的G-mean值；而只有当两者都较高时，才会得到高的G-mean 值。因此，G-mean 能衡量数据的整体分类性能。

下页表4展示了实验的对比算法。ADASYN、SMOTEENN、SMOTE-IPF、k-means SMOTE[20]、RSMOTE 和Adaptive-SMOTE 是流行的过抽样方法。表4 也给出了对比算法的参数。注意，本文把对比方法的参数设置为他们的标准版本。在提出的OMLSDE 中，本文需要去设置两个参数，即N和Fi。本文取N=2。本文采用文献[19]的建议来设置参数Fi（具体见式（11））。

表4 对比方法

在实验中，本文把k 近邻分类器（KNN，k=3）用作测试的分类器。本文用对比的过抽样方法（见表4）去改进不平衡的真实数据集（见表3）。然后，本文用KNN去测试对比方法的性能。

3.2 人工数据集上的实验

图3和图4展示了对比算法在人工数据集上的实验结果。其中，噪声与周围多数样本有不同的类标号。在图3和图4中，三角形的周围包含一些圆圈噪声。

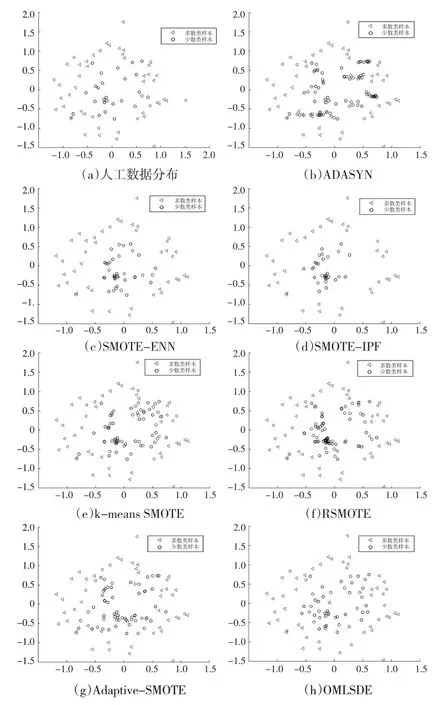
图3 对比算法在人工数据集1上的结果

图4 对比算法在人工数据集2上的结果

在图3和图4中，ADASYN和Adaptive-SMOTE会生成噪声。ADASYN会在更难学习的区域生成更多的少数类的合成样本（即边界上）。因此，在ADASYN中，原始数据集中的噪声会降低合成样本的质量。Adaptive-SMOTE用inner子集和danger子集去产生少数类的合成样本。但是原始数据集中的噪声和不安全的边界样本会降低inner 子集和danger子集的质量，从而使Adaptive-SMOTE生成噪声。

在图3 和图4 中，尽管k-means SMOTE 和RSMOTE 生成了相对安全的少数类的合成样本，但是他们不能去除原始数据集中的噪声。另外，SMOTE-ENN和SMOTE-IPF用噪声过滤器去移除原始数据集和合成样本中的噪声。但是，他们的噪声侦察技术依赖于参数，这导致表现不稳定。而且，他们会移除大量的少数类样本（即被识别的少数类的可疑噪声），这会造成信息损失。

图3 和图4 也显示，OMLSDE 能改变和优化噪声的位置和属性，而不是直接删除他们，这防止了信息损失。并且，OMLSDE用局部集合内的插值去生成安全的少数类的合成样本。

3.3 真实数据集上的实验

下页表5至表7展示了对比算法在真实数据集上的实验结果。在每一行中，本文用下划线来标出最高的值。

表5 对比算法在UCI数据集上的平均AUC结果（单位：%）

表5 展示了对比算法在真实数据集上的平均AUC值。OMLSDE 在10 个数据集上取得了最高的平均AUC值。在“平均值”行中，OMLSDE也取得了最高的所有数据集的平均AUC值。

表6展示了对比算法在真实数据集上的平均F-mea-sure 值。OMLSDE 在9 个数据集上取得了最高的平均F-measure值。在“平均值”行中，OMLSDE也取得了最高的所有数据集的平均F-measure值。

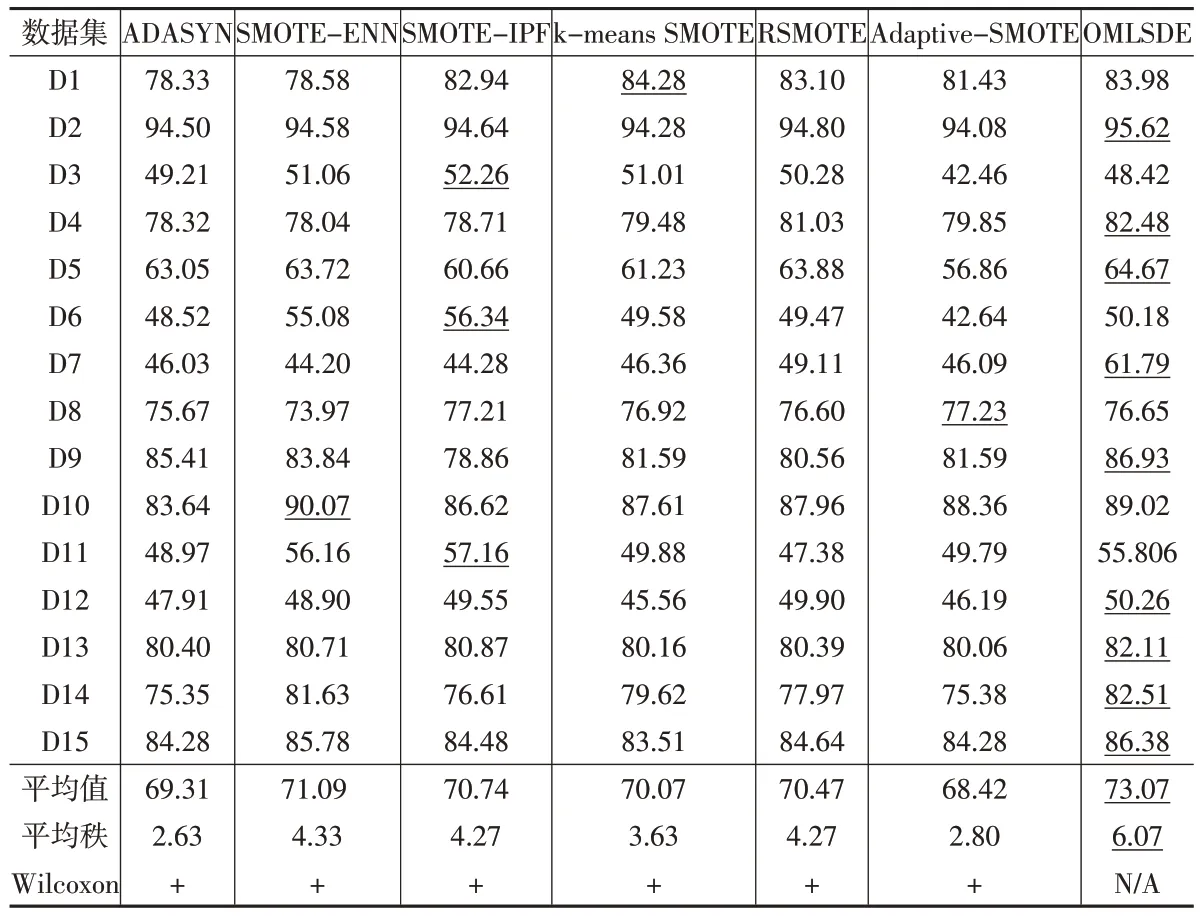
表6 对比算法在UCI数据集上的平均F-measure结果（单位：%）

表7展示了对比算法在真实数据集上的平均G-mean值。OMLSDE在11个数据集上取得了最高的平均G-mean 值。在“平均值”行中，OMLSDE 也取得了最高的所有数据集的平均G-mean值。

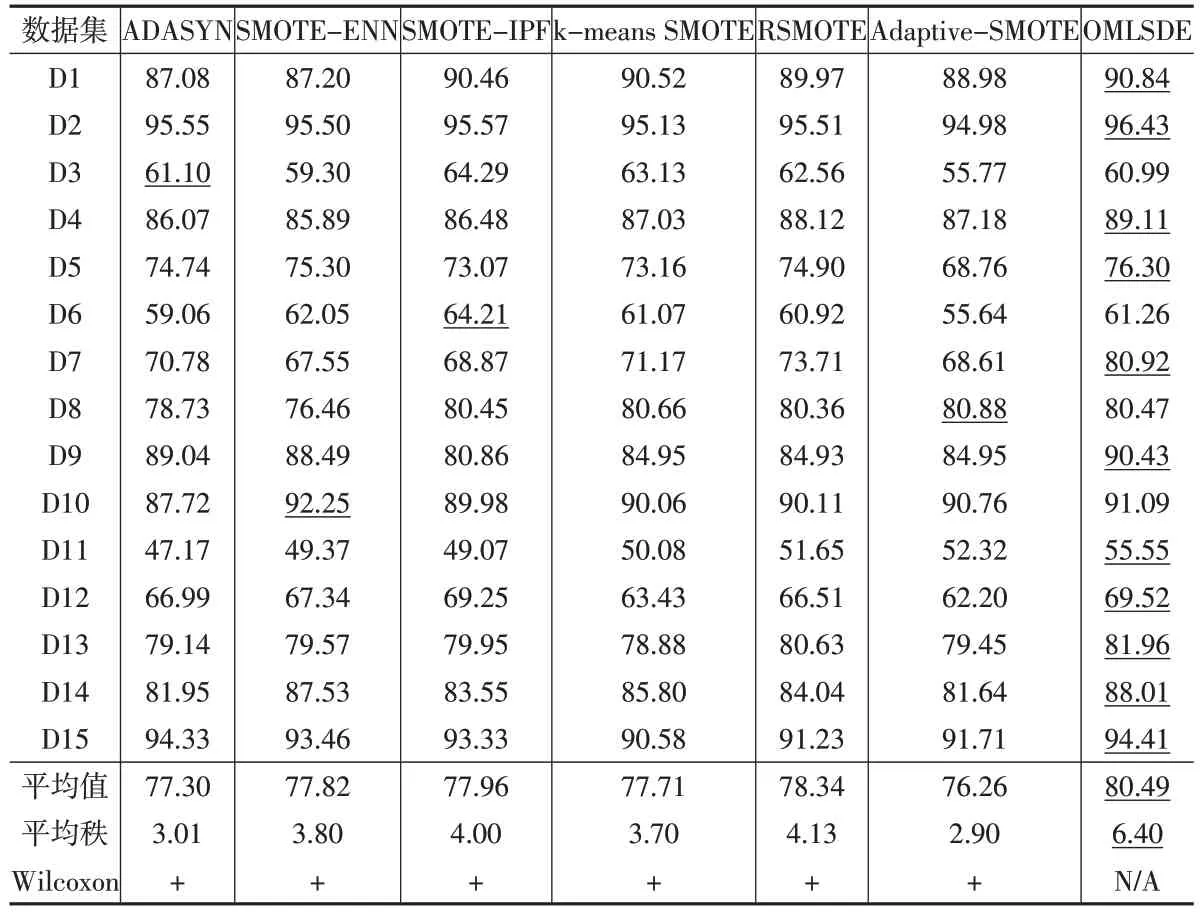
表7 对比算法在UCI数据集上的平均G-mean结果（单位：%）

本文也采用Friedmen检验来分析表5至表7的数据。本文设置Friedmen检验的显著性水平为0.05。表5 至表7 的“平均秩”行展示了Friedmen检验的平均秩的结果。如果一个算法性越好，那么它应该具有越高的平均秩的值。从表5至表7中可以看出，OMLSDE具有最高的平均秩。

另外，从表5 至表7 中还可以发现，OMLSDE 在German（D3）、Abalone（D6）、Spambase（D8）、Wisconsin Diagnostic Breast Cancer（D10)上表现一般。这是因为，没有一个算法能适应所有的数据分布。OMLSDE可能会在一些包含更多噪声的数据集明显地优于对比算法。

Friedmen检验结果显示，表5至表7的数据存在显著差别。因此，本文又使用Wilcoxon 符号秩检验来分析OMLSDE 是否与对比方法存在显著差别。本文设置Wilcoxon 符号秩检验的显著水平为0.05。如果OMLSDE显著优于对比方法，那么用符号“+”标记；如果OMLSDE显著劣于对比方法，那么用符号“-”标记；如果OMLSDE 与对比方法没有显著差别，那么用符号“～”标记。从表5 至表7 中“Wilcoxon”行的“+”可以看出，OMLSDE显著优于对比方法。

总的来说，表5至表7的数据证明，在改进少数类的分类正确率和总的分类效果上，OMLSDE 显著优于对比方法。这是因为OMLSDE具有如下优势：（1）噪声侦察技术是无参数化的；（2）合成样本的过程是无参化的；（3）OMLSDE能够去优化可疑的噪声，而不是直接删除他们，这防止了信息损失和改进了原始数据的分布。

4 结论

为了防止噪声生成和解决基于噪声过滤的过抽样方法的缺陷（噪声侦察技术和合成样本的过程依赖于参数；并且，他们会移除大量的少数类样本，造成信息损失），本文提出了一种基于局部集合和差分进化的过抽样方法OMLSDE。OMLSDE 的主要思路如下：首先，OMLSDE 计算每个样本的局部集合；其次，用局部集合和不平衡比去发现更多的多数类噪声，并且保留更多的少数类样本，以提高少数类的泛化性；然后，用差分进化去迭代地改变噪声的属性或位置，而不是直接移除他们；最后，用局部集合内的随机样本去生成少数类的合成样本。OMLSDE的时间复杂度是O(Gmax×NSE×C)+O(N×D×nmin)。

在仿真实验中，本文用2 个人工数据集、15 个真实数据集和6 个流行的过抽样方法来验证OMLSDE。结果显示：（1）OMLSDE 的噪声侦察技术不需要参数；（2）OMLSDE能有效防止噪声生成，优化噪声的属性，且避免信息损失；（3）就AUC、F-measure 和G-mean 指标而言，在训练KNN 分类器上，OMLSDE 明显优于6 个先进的过抽样方法。