飞机辅助动力装置转子平衡优化研究

张继鑫 吴蒙

摘 要：APU在工作過程中，由于转子件存在不平衡度，工作时会产生离心力，在离心力的作用下会促使轴在离心力方向产生挠度，进而进一步增大了不平衡度。由于不平衡度的存在，导致转子在运转过程中会产生振动，并且振动在临界转速附近尤为明显。转子本身的振动会导致轴的寿命下降，甚至突然损坏，静子的振动不但会损伤静子本身，亦会造成叶尖与机匣的刮磨，导致叶片或叶轮损坏，此外，密封装置也可能因为振动而导致损坏。本文的目的，则是通过APU转子单件平衡的数据来推算各转子件最佳装配位置，进而减小整体平衡时间，优化整体平衡效果。

关键词：动平衡；振动；平衡机

辅助动力装置是指航空器上主动力装置（发动机）之外可独立输出压缩空气或供电的小型辅助动力装置［1］。

根据APU厂家手册的规定，APU在装配过程中，需要进行转子的整体动平衡，以解决较大的不平衡度带来的影响。APU整体平衡时通过将各转子件旋转不同角度装配，使得每个转子的不平衡量能够相互抵消，进而达到配平目的。但目前各转子件之间相对位置关系的确定，都是依照经验和不断的测试来达到最终目的。这样对于转子个数较多或单个转子键齿数量较多的APU，转子间的搭配方式较多，平衡所需的时间也通常较长，进而增加时间成本。本文的目的则是通过理论计算的方式，计算出APU各转子的最佳相对位置关系，进而保证通过少量测试就可以达到手册的规定标准，从而降低维修成本。

1 转子动平衡相关概念

1.1 动不平衡

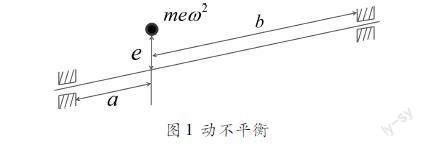
如果转子系统长度较大（转子厚度大或多转子件转子系统），由于质心处存在离心力，在工作时仍可产生不平衡力矩，使得支撑上受到交变载荷，引起整机振动。设转子的质量为m，其质心距离轴线存在偏心距e。当转子以工作转速ω运转时，质心处的离心力大小为meω2，则离心力在两支撑处产生的力矩大小分别为meω2及meω2b。

图1 动不平衡

由于转子运转时质心的位置也会发生变化，因此离心力虽然大小一定，但其作用于支撑处的弯矩在水平和竖直方向上的分量是不断变化的。以图1左支撑处弯矩的竖直方向分量为例，设转子运转时间为t，则左支撑处弯矩竖直分量为：

Mv=meω2a·cosωt

显然这是一种基本的简谐振荡，所以若转子件质心存在偏心距，工作过程中支撑受到的载荷是交变的［2］。这种不平衡称作动不平衡。生产中解决动不平衡问题主要从结构设计、装配工艺及平衡工艺方面入手。

1.2 转子类型

根据转子性质，转子类型可分为刚性转子和柔性转子（也称挠性转子）。其中，刚性转子的抗弯刚度较大，少量不平衡弯矩不会导致轴产生明显的挠度。在分析刚性转子时通常可忽略挠度带来的影响。柔性转子是指当工作转速高于一阶或二阶临界转速的转子，转子轴在临界转速处挠度最大，由于柔性转子在工作转速范围内会出现使转子轴线发生弯曲变形的临界转速，所以在分析柔性转子时挠度引起的离心力变化是不可忽略的。

2 平衡机动平衡计算原理

2.1 平衡机适用条件

由于平衡机设定转速通常远低于转子实际工作转速，所以使用平衡机进行转子动平衡，必须保证转子在两种转速下在支撑处等效的不平衡度基本相同，这就要求转子忽略挠度在不同转速下带来的影响。通常情况下，转子轴的抗弯刚性强、轴上所带的弯矩小，并且转子的工作转速远离临界转速，满足这三种条件的转子系统在计算时可忽略挠度带来的影响，并允许选择低转速平衡代替工作转速平衡，即使用平衡机进行平衡［3］。

2.2 平衡机计算原理

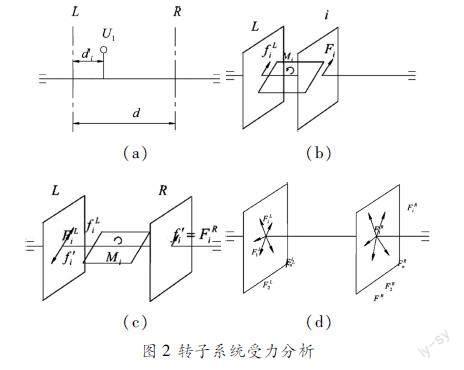
如图2（a）所示，假设一转子系统上Ui转子质心位于平面i上，左平面L与平面i的距离为di，右平面R与左平面的距离为d。现转子在平衡机的设定转速（远离临界转速）下进行运转，由于转子存在偏心距，在其质心处将产生沿径向外的离心力Fi，如图2（b）所示。现将Fi等效分解为一作用在左平面L上力fLi及一等效力矩Mi，由力学知识可知：

fLi=Fi  Mi=Fidi

在此基础上，将Mi进行进一步分解为作用于左平面L及右平面R上的一对力偶，如图2（c）所示，其中：

f′i=Mid  FRi=f ′i

再将左平面L上的力进行合成，得到：

FLi=fLi-f ′i

上述的FLi及FRi就是单一转子在左平面和右平面产生的不平衡力。对于整个转子系统来说，每个转子都可用同样的方法得出各自在左右平面上产生的不平衡力，如图2（d）所示，将这些力进行矢量求和，得到：

FL=∑FLi=mb1r1ω2  FR=∑FRi=mb2r2ω2

FL及FR则是转子系统在左右平面处的不平衡力，式中，mr表示转子系统在左右平面的动不平衡量。

上述分析方法称为多平面分离原理，分离平面越多，计算结果越精确。APU平衡所使用的平衡机通常选取两个平面进行不平衡量的计算［4］。

3 APU转子不平衡量计算

根据多平面分离原理，如果要计算APU转子系统整体的动不平衡量，需要知道单一转子的不平衡量及其不平衡量所在平面的位置。而在单件平衡时，我们能够通过平衡机上的数据确定各转子件在其两校正平面上的等效不平衡量，又因为在平衡前设定了两校正平面之间的距离，所以通过这三个参数便可以回推单一转子的不平衡量及其不平衡量所在平面的位置。这样，APU转子系统整体的动不平衡量便迎刃而解。

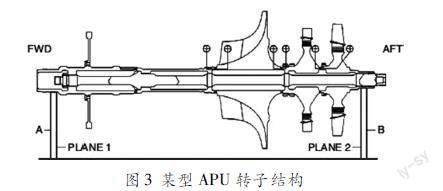
如图3所示，某型APU在整体平衡时，转子系统包括转子轴、负载段叶轮等效工装、中间轴、动力段叶轮、一级涡轮和二级涡轮。其中，负载段叶轮等效工装在平衡过程中会通过平衡机内置的补偿程序进行补偿计算，进而将其不平衡量补偿为0。所以在进行该型APU转子不平衡量计算时，只需要考虑中间轴、动力段叶轮、一级涡轮和二级涡轮。

首先分析中间轴的不平衡量。根据手册规定，设其平面一、平面二的距离为Da，经过平衡后，平衡机最后测定的平面一和平面二上的不平衡量分别为ma1ra1及ma2ra2。根据第三部分介绍的多平面分离原理：

平面一及平面二上的不平衡力

FL1=ma1ra1ω2  FR1=ma2ra2ω2

其中，ω为中间轴平衡时的设定转速。

由此可知

f′1=FR1=ma2ra2ω2

fL1=FL1+f ′i=（ma1ra1+ma2ra2）ω2

所以中間轴质心处由于不平衡量产生的离心力

F1=fL1=（ma1ra1+ma2ra2）ω2

设中间轴不平衡量为mara，那么

mara=ma1ra1+ma2ra2

又因为等效不平衡力矩

M1=f′1Da=ma2ra2ω2Da

所以中间轴不平衡量所在平面和其平面一之间的距离

d1=M1F1=ma2ra2ma1ra1+ma2ra2Da

同理，亦可推导出动力段叶轮的不平衡量

mbrb=mb1rb1+mb2rb2

动力段叶轮不平衡量所在平面和其平面一之间的距离

d2=mb2rb2mb1rb1+mb2rb2Db

其次，分析一级涡轮和二级涡轮的不平衡量。一级涡轮和二级涡轮在进行单件平衡时，和其他转子有所不同，由于一二级涡轮的厚度很小，且在叶片装配后，涡轮组件的质心处于涡轮盘前后平面之间，所以在进行一二级涡轮的平衡时，我们往往采用静平衡的方式来最终保证不平衡量在允许范围内。根据静不平衡度的概念，涡轮组件质量和偏心距的乘积就是在整体动平衡计算时所需要的不平衡量。这里设一级涡轮的不平衡量为mcrc，二级涡轮的不平衡量为mdrd。

最后进行APU转子整体动平衡不衡量的推导。由于APU转子整体动平衡采用合理分配各转子不平衡量位置的方式来达到平衡目的，所以只需要确定各转子间的相对位置关系即可。

现设定中间轴不平衡量位置为0°位置，设动力段叶轮、一级涡轮和二级涡轮不平衡量位置与中间轴不平衡量位置沿轴向观察的夹角为θb、θc和θd。由于各转子件是由键齿相啮合的，所以转子件可旋转的角度只能是一个键齿角度的整数倍，因为该型APU每个转子件有16个键齿，所以转子件每次可旋转的角度为22.5°的整数倍。

由于转子件之间的不平衡量位置不能完全对正（夹角为0°），所以我们设定动力段叶轮、一级涡轮和二级涡轮不平衡量位置与中间轴不平衡量位置大于0°的最小夹角分别为θb0、θc0和θd0。那么，

θb=θb0+n1π8（n1∈Z，015）θc=θc0+n2π8（n2∈Z，0

通过前述计算，我们得到了各转子件不平衡量所在平面的位置，那么通过测量则可以进一步确定该平面到整体平衡平面一的距离。现设定中间轴、动力段叶轮、一级涡轮和二级涡轮不平衡量所在平面的位置到整体平衡平面一的距离分别为DA、DB、DC和DD，整体平衡平面一和平面二之间的距离为D。

根据前述多平面分离原理，中间轴在平面一和平面二上不平衡量分量

FLa=maraω2（1－DAD）  FRa=maraω2DAD

其中ω为整体平衡时平衡机的设定转速。

同理，动力段叶轮在平面一和平面二上不平衡量分量

FLb=mbrbω2（1－DBD）  FRb=mbrbω2DBD

一级涡轮在平面一和平面二上不平衡量分量

FLc=mcrcω2（1－DCD）  FRc=mcrcω2DCD

二级涡轮在平面一和平面二上不平衡量分量

FLd=mdrdω2（1－DDD）  FRd=mdrdω2DDD

设0°位置为y轴正方向，对平面一和平面二上的分力进行矢量求和。首先将平面一上的力进行正交分解，得到水平方向的分力

FLH=FLbsinθb+FLcsinθc+FLdsinθd

同理，平面一上垂直方向的分力

FLV=FLa+FLbcosθb+FLccosθc+FLdcosθd

矢量求和得到平面一上产生的不平衡力

FL=FL2H+FL2V

同理，平面二上水平和垂直方向的分力

FRH=FRbsinθb+FRcsinθc+FRdsinθd

FRV=FRa+FRbcosθb+FRccosθc+FRdcosθd

平面二上产生的不平衡力

FR=FR2H+FR2V

FL和FR除以平衡机设定转速ω的平方即可得到平衡机上显示的整体平衡的不平衡量大小。

4 优化方案的检验

FL和FR的变化与转子件之间的相对位置有关，即与θb、θc和θd的取值有关。而θb、θc和θd的取值又和转动的键齿数，即n1、n2和n3有关。n1、n2和n3为大于等于0小于等于16的任意整数，所以整体平衡的搭配方案共有16的三次幂，即4096种。对于该类离散型变量求最优解的问题，遗传算法、粒子群算法、蚁群算法等方式均能够取得不错的效果［5］。

在求得最优解后，本文采用申克的HL2BU型平衡机对转子系统的平衡效果进行了测试。经过若干台的检测，该优化方案能够稳定地确保转子的剩余不平衡量符合手册的公差要求。

5 结论

基于多平面分离原理可以准确地解得APU转子的不平衡量，在此基础上，可通过相应算法求得最优解，进而降低转子振动，保证APU装配后运行的可靠性。此外，本文的方案使得装配过程能够从一次次的经验测试转变为理论运算直接得出结论，亦可大大减少装配周期，节约时间成本。

参考文献：

［1］马广文．交通大辞典［M］.上海：上海交通大学出版社，2005.

［2］孙爱俊，张莹，但敏，等.航空发动机强度与振动［M］.北京：中国民航出版社，2014.

［3］国家仪器仪表工业总局.中华人民共和国专业标准.2：试验机术语ZB Y033－82［M］.北京：标准化研究室，1982.

［4］汤秉辉.动平衡机之多平面分离原理与应用［D］.臺湾：中原大学，1991.

［5］包强.一种求解旅行商问题的混合遗传模拟退火算法［J］.中国储运，2021（11）：204205.

作者简介：张继鑫（1996— ），男，汉族，辽宁鞍山人，硕士，助理工程师，研究方向：APU维修与故障诊断；吴蒙（1995— ），女，汉族，辽宁鞍山人，硕士，助理工程师，研究方向：激光制孔及切割。