采用弹体追踪导引律的旋转弹锥形运动稳定性
宋金超,赵良玉
(北京理工大学 宇航学院,北京 100081)
0 引言
随着信息化和智能化战争时代的来临,未来战场环境日益复杂,制导武器也朝着智能化、多样化、低成本化和协同一体化发展。旋转弹凭借其提高突防能力、降低制造成本并简化控制系统结构等独特优势,在制导武器序列中牢牢占据着不容忽视的一席之地,受到了世界各军事强国的广泛关注和大力发展[1-3]。与非旋转弹不同,旋转弹在飞行过程中存在着由自旋引起的弹体俯仰和偏航通道耦合,并可能导致弹体出现不收敛的锥形运动,从而发生射程降低甚至中途掉弹的现象[4-5]。从20世纪50年代开始,锥形运动稳定性一直是旋转弹领域的研究重点和热点,国内外专家学者均对其进行了系统深入的研究,并得到了一系列的旋转弹动态稳定性条件[6-9]。
固联于弹体的全捷联导引头由于生产成本低、结构简单且可靠性高,成为低成本末制导旋转弹用来获取目标信息的优先选择。由于捷联导引头与弹体固联并跟随弹体一起旋转,其响应延迟和陀螺标度因数误差则可能会影响锥形运动的稳定性,并因此显著减小制导控制系统的稳定区域[10-13]。Park[14]针对带有捷联导引头的旋转弹,分析了导引头视线角约束对其动态稳定性的影响。对于捷联导引头来说,视线角速度信息不能直接测量,需要通过综合导引头与弹载角速率陀螺仪的测量值得到。这两个元件动力学模型的差异,将不可避免地在制导控制系统中引起额外的寄生回路,从而对弹体的系统稳定性产生影响。对此,Li等[15]考虑导引头干扰抑制率引起的寄生回路对弹体姿态的影响,推导出相应的动态稳定性条件。Zheng等[16]考虑雷达天线罩引起的寄生回路影响,对系统的稳定性进行了分析。同时,捷联导引头和角速率陀螺之间存在的标度因数差异,会对旋转弹体锥形运动稳定性产生影响,He等[17]建立了标度因数误差引发的寄生回路作用下的旋转导弹锥形运动稳定性条件。Hu等[18]对采用比例导引方式的旋转弹动态稳定性进行了研究,并基于线性化的动力学模型,建立了其动态稳定的充要条件。然而,已有文献均未对弹体追踪导引方式的旋转弹锥形运动稳定性进行研究。
弹体追踪导引律可以避免采用传统比例导引律攻击机动目标时视线角速度发散的问题,从而保证导引头有效探测、追踪目标,具有一定的工程应用价值。一些末制导旋转弹为保证其低成本、易装配、便发射等优势,常采用弹体追踪导引律来保证打击精度,如某型采用捷联式半主动激光导引头的旋转弹就采用了弹体追踪导引律[19]。这类旋转弹直接使用姿态角反馈信息生成控制指令,与采用比例导引律的制导控制系统相比具有较大区别,有必要对其可能诱发的锥形运动稳定性进行深入研究。
本文在考虑捷联导引头响应延迟和角速率陀螺仪标度因数误差的情况下,对使用弹体追踪导引律的旋转弹动态稳定性进行研究。首先在非旋转弹体坐标系中,推导了随弹体旋转的捷联导引头动力学模型,并结合弹体动力学模型构造了复数形式的弹体追踪制导控制系统模型;接着,分别考虑捷联导引头响应延迟和角速率陀螺仪标度因数误差的影响,通过数学仿真得到制导控制系统的稳定区域,并进行算例验证。通过分析发现,导引头响应延迟和陀螺标度因数误差均对稳定区域有一定影响,且阻尼回路可以显著提高稳定区域上限,但弹体转速的提高会减小稳定区域上限。
1 捷联导引头弹体追踪制导控制系统
1.1 坐标系定义及转换
旋转弹一般具有轴对称结构,可以假设其在滚转过程中,任意位置均具有相同的空气动力学特性及惯性质量特性。因此,一般在非旋转坐标系下对其制导控制系统进行建模分析。本文主要围绕末制导旋转弹的锥形运动稳定性开展研究,使用的坐标系包括非旋转弹体坐标系和旋转弹体坐标系。
非旋转弹体坐标系Oxnynzn:坐标原点为旋转弹弹体瞬时质心的位置O;Oxn轴与弹体纵轴重合,指向头部为正;Oyn轴位于铅垂面内,与Oxn轴垂直且指向上方为正;Ozn轴垂直于Oxnyn平面并通过右手定则确定。
旋转弹体坐标系Oxbybzb:坐标原点为旋转弹瞬时质心的位置O;Oxb轴与弹体纵轴重合,指向头部为正;Oyb轴位于弹体纵向对称面内,与Oxb轴垂直且指向上方为正;Ozb轴垂直于Oxbyb平面并通过右手定则确定。
由于非旋转弹体坐标系是系统的参考坐标系,需要将旋转弹体坐标系中测量得到的误差角速度变换到非旋转弹体坐标系中,从而在非旋转弹体坐标系中产生追踪制导指令,二者之间的转换关系如图1所示。
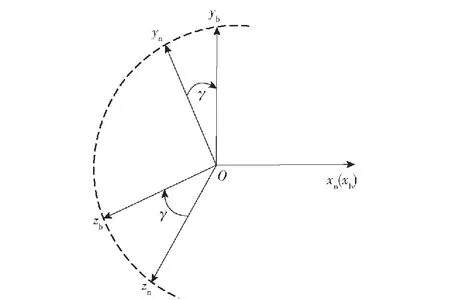
图1 非旋转弹体坐标系与旋转弹体坐标系之间的转换Fig.1 Conversion between non-spinning and spinning missile coordinate systems
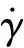
(1)
1.2 旋转弹的运动学方程
旋转弹在飞行过程中的质心动力学方程[20]和绕质心转动运动学方程分别为
(2)
(3)
式中:u、v、w分别为非旋转弹体坐标系下的导弹速度;p、q、r分别为非旋转弹体坐标系下的导弹角速度;Fx、Fx、Fz分别为作用在旋转弹上的空气动力;P为推力;m为旋转弹质量;g为重力加速度;ψ为旋转弹偏航角姿态角;ϑ为旋转弹俯仰角姿态角;Mx、My、Mz为作用在旋转弹上的气动力矩;Ix和It为极转动惯量和赤道转动惯量。


图2 攻角侧滑角示意图Fig.2 Angle of attack and angle of side-slip
导弹速度矢量可表示为
(4)
且有
α=arctan(w/u),β=arcsin(v/V)
(5)
式中:V为导弹速度标量。
引入复变量:复攻角σ=β+iα,复姿态角ξ=ψ+iϑ,复舵偏角指令δ=-δz+iδy。
对于采用较小尺寸舵片的鸭式低速制导旋转弹而言,其马格努斯力和鸭舵产生的升力相对较小,因此在稳定性分析中可以将其忽略。仅考虑线性化后的气动力,并且将攻角和侧滑角视为小量,则施加于弹体的气动力可以表示为
(6)
式中:Q为动压,Q=ρV2/2,ρ为空气密度;S为参考面积;CD为弹体阻力系数;CLα为弹体升力系数对攻角的斜率。
在非旋转弹体坐标系中,作用于导弹的气动力矩为
(7)
式中:l为特征长度;C1和Clp分别为导转力矩系数和滚动阻尼力矩系数;Cmα为静态力矩系数;Cmpα为马格纳斯力矩系数;Cmq为横向阻尼力矩系数;Cmδ为控制力矩系数。
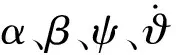
(8)
忽略式(5)、式(6)中的高阶项,导弹的横向运动方程可以写为
(9)
可以简写为
(10)
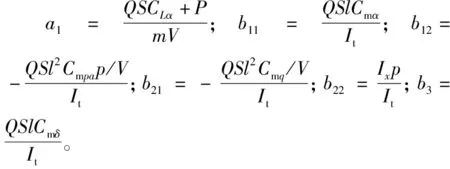
弹体的横向即俯仰和偏航通道的过载可以表达为
(11)
1.3 弹体追踪导引律的弹目视线关系
以采用轴对称弹体结构和鸭式气动布局的末制导旋转弹为例,在弹体追踪导引律的作用下,弹体纵轴在攻击目标过程中始终努力指向目标[22]。对于轴对称弹体而言,其在俯仰和偏航方向具有相同的运动特性,以图3所示俯仰平面弹目视线(LOS)关系为例:图3中,qy为非旋转弹体坐标系中俯仰平面的真实弹目视线角,εy为弹目视线和弹体纵轴之间的误差角,xg为基准线,xs为弹目视线,Vr为弹体相对于目标的速度。。
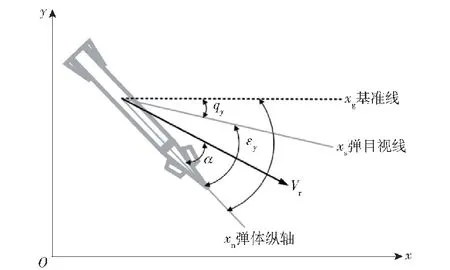
图3 俯仰平面弹目视线关系图Fig.3 Relationship of missile-to-target LOS in pitch plane
与平台导引头不同,捷联导引头与旋转弹弹体固联,视线角信息无法直接测量获得。需要用陀螺仪测量的姿态角速度减去通过导引头得到视线与弹体坐标系纵轴之间的误差角速度,从而得到视线角速度。通过图3中的弹目视线之间关系可以得到,俯仰平面的视线角可表示为
qy=ϑ-εy
(12)
使用弹体追踪导引律时,由于存在弹目视线与弹体纵轴的偏差[23],为了使二者重合引入的俯仰平面视线角速度可以表示为
(13)
对于鸭式布局的弹体结构,正的舵偏角将引起正的攻角和正的侧滑角,正的非旋转攻角将产生正的俯仰加速度,正的侧滑角将产生负的偏航加速度[24]。得到偏航平面的视线角为
qz=ψ-εz
(14)
则偏航平面的视线角速度为
(15)
式中:qz为非旋转弹体坐标系中偏航平面的真实弹目视线角;εz为弹目视线和弹体纵轴之间的误差角。
由图3可知,俯仰平面的弹体追踪导引律可描述为
ϑc=qy
(16)
即姿态角控制指令等于弹目视线角,ϑc为俯仰平面的控制指令。将式(16)代入式(12)中可知,当使用俯仰角ϑ反馈回路进行控制时,可以得到
εy=ϑ-ϑc
(17)
同样,得到偏航方向弹体追踪制导律方程为
εz=-ψ-(-ψc)
(18)
式中:ψc为偏航平面的控制指令。
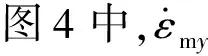
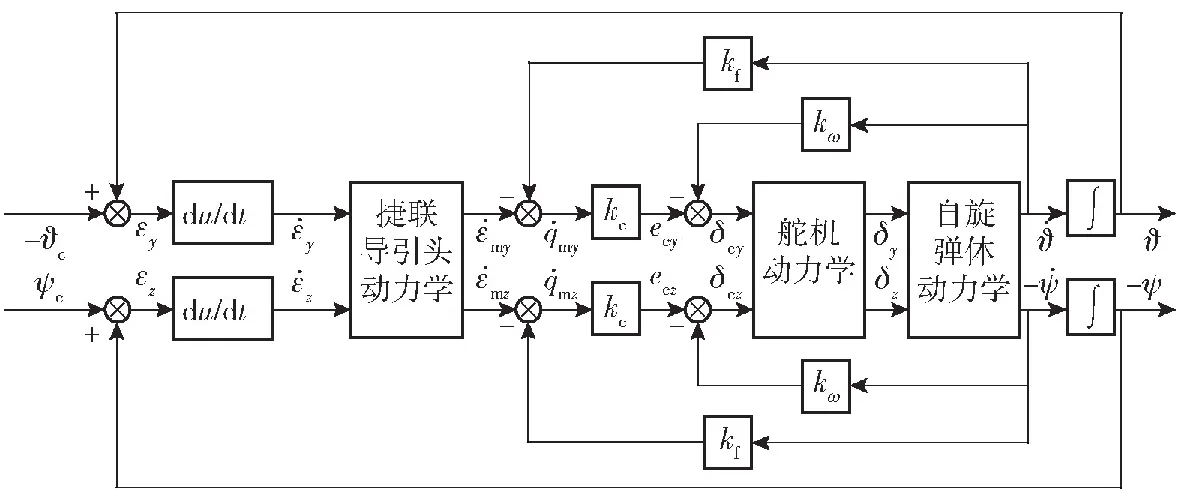
图4 捷联导引头弹体追踪系统结构图Fig.4 APG system of the strapdown seeker
1.4 旋转弹的动力学方程
(19)
(20)
根据文献[10]和文献[11]可以得到捷联导引头在弹体坐标系下的动力学方程:
(21)
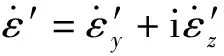
(22)
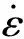
(23)
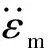
(24)
因此,非旋转弹体坐标系中导引头系统输入和输出之间的关系为
(25)
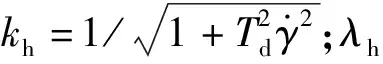
(26)
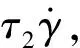
(27)
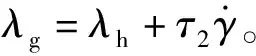
(28)
根据图4所示的捷联导引头弹体追踪系统结构图,可以得到非旋转弹体坐标系下用于弹体追踪制导方式的测量视线角速度:
(29)
由于捷联导引头存在响应延迟,旋转弹俯仰和偏航通道中测得的视线角速度将会发生交叉耦合,耦合后的制导指令为
(30)
1.5 舵机系统控制指令
舵面偏转指令由制导指令转换得到,如图4所示。对具有姿态角反馈回路的控制系统,其舵机控制指令δcy和δcz[4]可表示为
(31)
将式(30)代入式(31)中,得到非旋转弹体坐标系中的舵偏角指令为
(32)
为便于对系统进行动态稳定性分析,在姿态控制指令为零时,即姿态角速度指令为零时对弹体锥形运动稳定性进行分析,式(32)可以改写为
(33)
在旋转弹运动的过程中,恒定指令将使鸭式舵生成谐波响应。考虑固有频率1/Ts、阻尼比μs、指令传输延迟τ1,对舵机系统进行建模。得到非旋转弹体坐标系中舵机输入和输出之间的关系[20]为
(34)
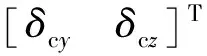
(35)
旋转运动下舵机系统的动力学增益为
(36)
舵机的总延迟角为
(37)
2 考虑导引头响应延迟的旋转弹稳定性分析
2.1 系统的动态稳定性条件
(38)
将式(10)、式(33)、式(34)、式(38)整合,可以得到复数形式下的旋转弹制导控制线性化方程:
(39)
式中:ksr=kskr;kdh=kdkh。
基于式(39),可以得到旋转弹制导控制系统的线性化微分方程为
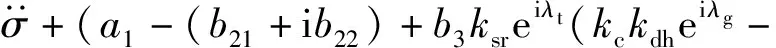
(40)
式(40)的特征方程为
λ2+(m1+in1)λ+(m2+in2)=0
(41)
式中:
(42)
(43)
定义多项式F0=λ2+(m1+in1)λ+(m2+in2)和F1=m1λ2+in2,连分式的展开形式可以写为
(44)
根据复系数系统稳定性定理[20],式(44)所有根的实部在复平面左半边的充分必要条件是r1>0且r2>0,因此该系统动态稳定性条件可以写为
(45)
2.2 不考虑导引头响应延迟
假设捷联导引头不存在相位滞后和稳态误差,也不存在信号解算延迟,设导引头系统增益kd=1,则且λg=0。在不考虑导引头响应延迟的情况下,通道之间的耦合作用可以忽略,因此可忽略升力、推力以及旋转弹的位移运动,弹体的姿态运动可以仅用攻角运动来描述,即a1=0。对于低转速制导旋转弹而言,其马格努斯力矩和陀螺力矩项相对较小,因此在稳定性分析中可以将其忽略,即b12=0且b22=0,忽略小量a1b21。在不考虑陀螺标度因数误差的情况下,kf=1。因此,可以将式(42)、式(43)简化写为
(46)
(47)
得到简化后的稳定条件为
(48)

系统增益ksr的表达式为
(49)
式中:ks为舵机系统增益,是个常数。
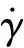

表1 旋转弹参数表Table 1 Parameters of spinning missile

表2 无延迟角的制导回路增益下限Table 2 Lower limit of the control and guidance loop gain without delay angle
2.3 考虑导引头响应延迟
捷联导引头的响应延迟会导致偏航、俯仰两个通道测得的视线角速度产生耦合,进而导致制导指令交叉耦合,从而系统的稳定条件发生变化,系统稳定的充要条件为式(45)。同样忽略马格努斯力矩和陀螺力矩项,即b12=0且b22=0。同时考虑捷联导引头的时间常数Td相对较小,则导引头的动态增益可以假定为kh=1,且认为导引头的延迟角λg为小量。因此有cosλg≈1和sinλg≈λg。导引头系统增益kd通常取1,忽略小量a1,b21,可以将式(42)、式(43)化简为
(50)
(51)
该系统的动态稳定性条件仍为式(45),将式(50)、式(51)代入式(45),得到稳定条件为
(52)
在旋转弹的设计中,通常限制舵机总延迟角λt≤90°,因此下列讨论都建立在此基础上。由于b3>0,则式(52)中的第1式可以化简为
(53)
式(52)中第2式为制导回路增益kc关于阻尼回路增益kω的3次不等式。由于计算比较复杂,不便于直观分析,因此采用数值方法分析制导回路对锥形运动稳定性的影响。控制指令增益的下限为式(53),对制导回路增益kc上限进行求解。旋转弹锥形运动的稳定性与制导控制系统的制导回路增益kc及阻尼回路增益kω相关,因此稳定区域上限通过对两个回路增益进行设计得到。同样基于表1给出的旋转弹参数,使用数值方法可确定弹体的稳定性条件。
考虑导引头响应延迟,分别令导引头延迟角为λg=3°和λg=6°,得到在不同弹体转速及阻尼回路增益时,使系统稳定的制导回路增益取值上限,分别如表3和表4所示。
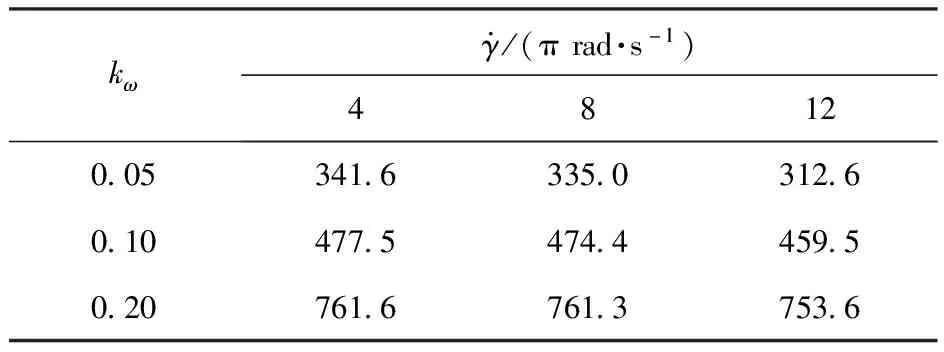
表3 λg=3°制导回路增益上限Table 3 Upper limit of the loop gain with λg=3°

表4 λg=6°制导回路增益上限Table 4 Upper limit of the loop gain with λg=6°
对比分析表2、表3和表4可以得出,当不存在导引头延迟时,使系统稳定的kc仅在下限。当存在导引头延迟的情况下,若其他参数不变,则导引头延迟对使系统稳定的制导回路增益有消极影响,会导致原本仅存在下限的系统稳定的制导回路增益出现上限。且延迟角越大,系统稳定的kc上限越小。当延迟角增大一倍时,系统稳定的制导回路增益上限减小一半。同时可以看出,系统稳定的控制回路增益上限随阻尼回路参数增大而增大,随转速增大而减小,说明阻尼回路可以提高稳定上限,而转速增加会降低稳定上限。
2.4 案例分析
分别选取不同弹体转速和阻尼回路增益,对2.2节及2.3节中得到的制导回路增益稳定上限,进行算例验证。
首先对不考虑导引头响应延迟的制导控制系统进行数值仿真,选取不同的弹体转速和阻尼回路增益,分别验证系统在不同制导回路增益下的稳定性。
图5(a)给出了弹体转速p=4π rad/s,阻尼回路增益kω=0.05,制导回路增益kc=2时的弹体复攻角ξ=β+iα的变化情况,此时kc满足系统动态稳定性条件,可观察到该锥形运动的收敛现象。当p=8π rad/s、kω=0.1、kc=200时,如图5(b)所示,弹体锥形运动同样收敛。图5(c)给出了p=12π rad/s、kω=0.2、kc=1 000时系统稳定的情况。

图5 不考虑导引头响应延迟的收敛锥形运动Fig.5 Convergent coning motion without considering seeker delay response
然后对考虑导引头响应延迟的制导控制系统进行数值仿真,选取导引头延迟角λg=3°,弹体转速p=8π rad/s,阻尼回路增益kω=0.1。图6给出了kc=400时的弹体复攻角ξ=β+iα的变化情况,此时kc满足系统动态稳定性条件,可观察到该锥形运动的收敛现象。当kc=474.4时,弹体锥形运动处于临界稳定状态,此时复攻角处于等幅振荡状态(见图7)。图8给出了kc=500时复攻角的变化情况,此时制导回路增益kc大于稳定上限,锥形运动出现发散。
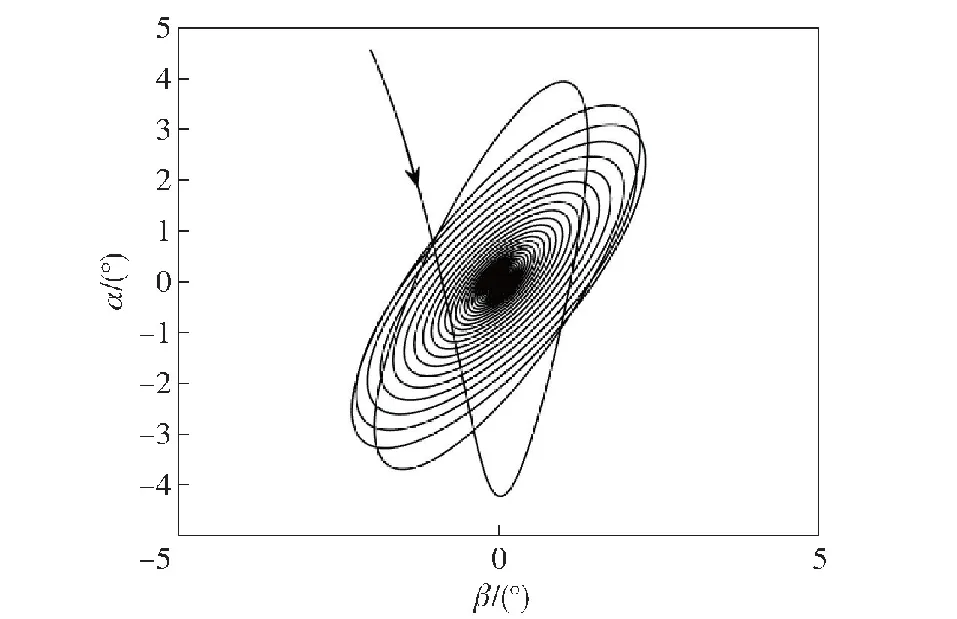
图6 λg=3°时收敛的锥形运动Fig.6 Convergent coning motion with λg=3°
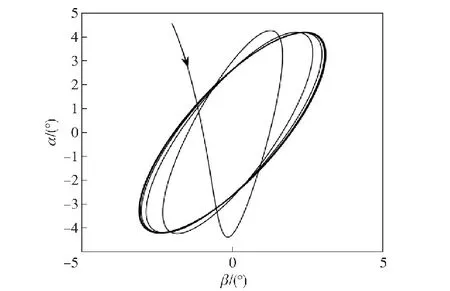
图7 λg=3°时弹体临界稳定的锥形运动Fig.7 Critical stable coning motion with λg=3°
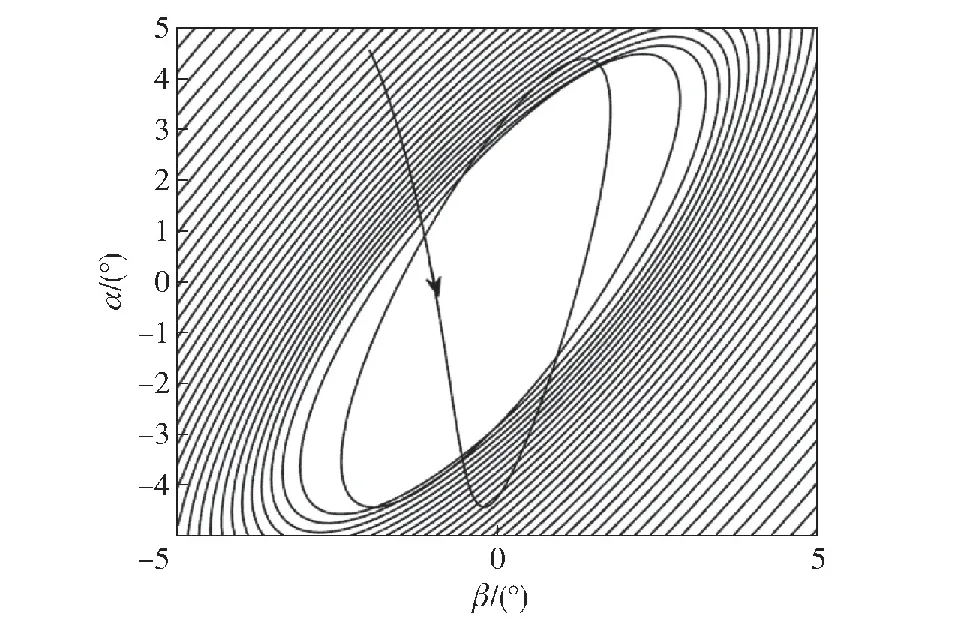
图8 λg=3°时弹体发散的锥形运动Fig.8 Divergent coning motion with λg=3°
选取导引头延迟角λg=6°,弹体转速p=4π rad/s,阻尼回路增益kω=0.05。
图9给出了kc=100时的弹体复攻角ξ=β+iα的变化情况,此时kc满足系统动态稳定性条件,可观察到该锥形运动收敛。当kc=161.9时,弹体锥形运动处于临界稳定状态,此时复攻角等幅振荡(见图10)。图11给出了kc=250时复攻角的变化情况,此时制导回路增益大于稳定上限,锥形运动出现发散。

图9 λg=6°时收敛的锥形运动Fig.9 Convergent coning motion with λg=6°
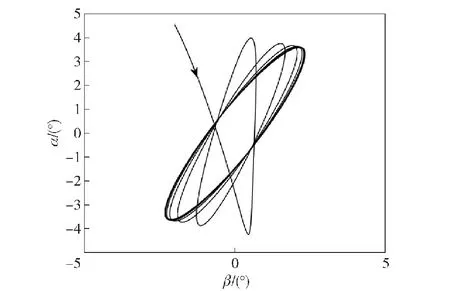
图10 λg=6°时弹体临界稳定的锥形运动Fig.10 Critical stable coning motion with λg=6°
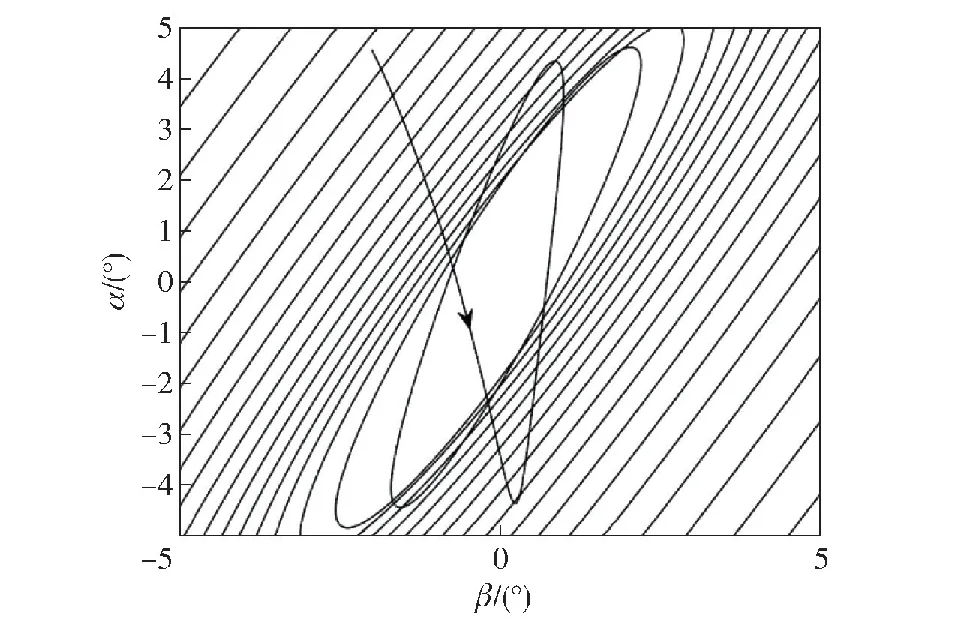
图11 λg=6°时弹体发散的锥形运动Fig.11 Divergent coning motion with λg=6°
根据仿真图5~图11可以看出,在不同的导引头延迟角、弹体转速及阻尼回路增益下,数值解得的旋转弹稳定上限与仿真结果高度一致,证明了第1节和第2节理论分析和数值解算方法的正确性。
3 考虑陀螺标度因数误差的稳定性分析
根据图4及式(23),当陀螺存在标度因数误差时,误差系数kf≠1,分别在不考虑导引头响应延迟和考虑导引头响应延迟的情况下,分析陀螺标度因数误差对旋转弹稳定性的影响。
3.1 不考虑导引头响应延迟
在不考虑导引头响应延迟的情况下,有kdh=1且γg=0,此时指令之间不存在耦合,可以忽略升力、推力以及旋转弹的位移运动,弹体的姿态运动可以仅用攻角运动来描述,即a1=0。
对于低速制导旋转弹而言,忽略马格努斯力矩和陀螺力矩,即b12=0且b22=0。可以将式(42)简化为
(54)
式(43)仍可化简为式(47)。
系统稳定条件与2.2节中的式(45)相同。得到简化的稳定条件为
(55)
在陀螺标度因数误差为kf=1.004及kf=0.996时,使用表1所示的旋转弹参数,在不同的阻尼回路增益及弹体转速下,使用数值方法确定弹体的稳定性条件如表5及表6所示。
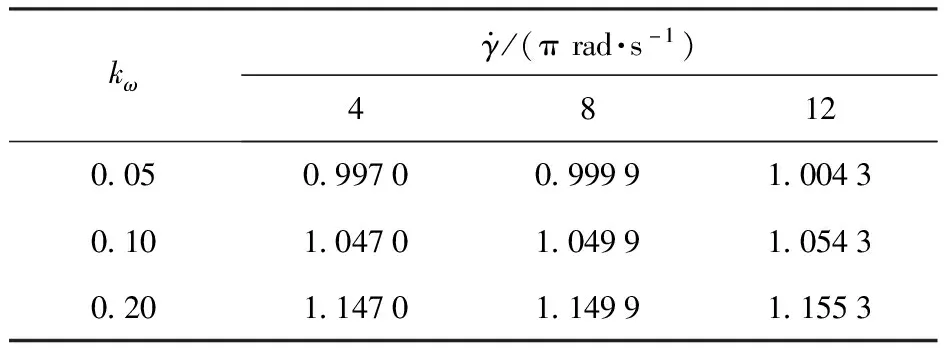
表5 kf=1.004无延迟角的制导回路增益上限Table 5 Upper limit of the loop gain at kf=1.004
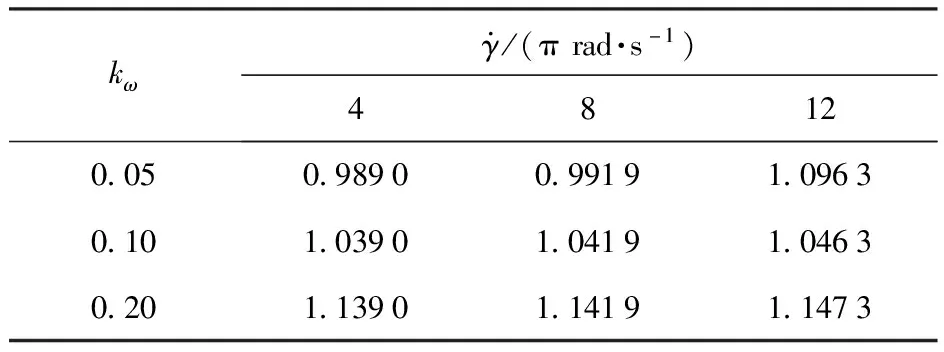
表6 kf=0.996无延迟角的制导回路增益上限Table 6 Upper limit of the loop gain at kf=0.996
3.2 考虑导引头响应延迟
对于末制导旋转弹,在考虑捷联导引头响应延迟的情况下,再综合考虑陀螺标度因数误差,仍然满足b12=0且b22=0、导引头的动态增益可以假定为kh=1,cosγg≈1和sinγg≈γg。导引头系统增益kd
通常取1,忽略小量a1b21,式(42)、式(43)可以化简为
(56)
(57)
下列讨论同样建立在γt≤90°的基础上,由于a1-b21>0,则式(55)中的第1式恒成立。使用复数线性系统稳定性判别方法,可获得解析式的稳定性条件,但计算比较复杂,不便于直观分析。采用数值方法分析制导回路对锥形运动稳定性的影响,此时旋转弹锥形运动的稳定性与制导控制系统的制导回路增益kc及阻尼回路增益kω相关,故稳定区域通过对两个回路增益进行设计得到。基于表1所示的旋转弹参数,使用数值方法来确定弹体的稳定性条件。
分别令导引头延迟角为λg=3°和λg=6°。使系统稳定的控制制导回路增益下限为kc>0,分别求得陀螺标度因数误差为kf=1.004及kf=0.996时,在不同弹体转速及阻尼回路增益下,使系统稳定的控制制导回路增益取值上限如表7~表10所示。

表7 kf=1.004,λg=3°制导回路增益上限Table 7 Upper limit of the loop gain with, kf=1.004,λg=3°

表8 kf=0.996、λg=3°制导回路增益上限Table 8 Upper limit of the loop gain with kf=0.996,λg=3°
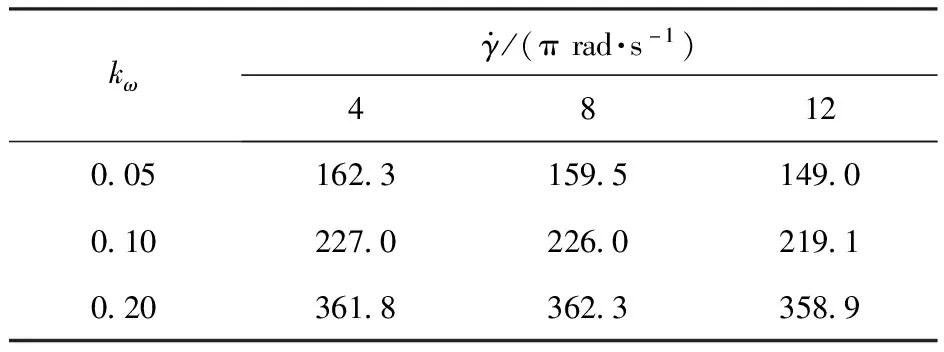
表9 kf=1.004、λg=6°制导回路增益上限Table 9 Upper limit of the loop gain with kf=1.004,λg=6°

表10 kf=0.996、λg=6°制导回路增益上限Table 10 Upper limit of the loop gain with kf=0.996,λg=6°
将表7~表10进行对比可知,考虑陀螺标度因数误差时,在其他参数不变的情况下,系统稳定的制导回路增益上限随阻尼回路参数增大而增大,随转速增大而减小,说明阻尼回路可以显著提高稳定上限,而转速增加会降低稳定上限。在其他参数不变的情况下,陀螺标度因数误差对稳定区域上限有较小的影响,且当标度因数误差系数大于1时且增大0.4%时,稳定上限会变大0.5%;标度因数误差系数小于1且减小0.4%时,稳定上限会变小0.5%。
3.3 案例分析
分别选取不同的弹体转速和阻尼回路增益,对3.1节及3.2节中得到的制导回路增益上限,进行算例验证。
首先对不考虑导引头响应延迟,仅考虑陀螺标度因数误差的制导控制系统进行数值仿真,选取不同的弹体转速和阻尼回路增益,分别验证系统在不同制导回路增益下的稳定性。
设置陀螺标度因数误差系数kf=1.004。图12(a)给出了p=4π rad/s、kω=0.05、kc=5时的弹体复攻角ξ=β+iα的变化情况,此时kc满足系统动态稳定性条件,可观察到该锥形运动的收敛现象。图12(b)给出了p=8π rad/s、kω=0.10、kc=50时弹体锥形运动的收敛情况。图12(c)给出了p=12π rad/s、kω=0.20、kc=300时锥形运动收敛的情况。

图12 仅考虑陀螺标度因数误差的收敛锥形运动Fig.12 Convergent coning motion considering the gyro scale-factor error
然后,考虑导引头响应延迟,对不同延迟角和陀螺标度因数下的旋转弹锥形运动稳定性进行仿真验证。选取弹体转速p=8π rad/s,阻尼回路增益kω=0.10,导引头响应延迟角λg=3°,陀螺标度因数误差kf=1.004。图13给出了kc=450时的弹体复攻角ξ=β+iα的变化情况,此时kc满足系统动态稳定性条件,可观察到该锥形运动收敛。
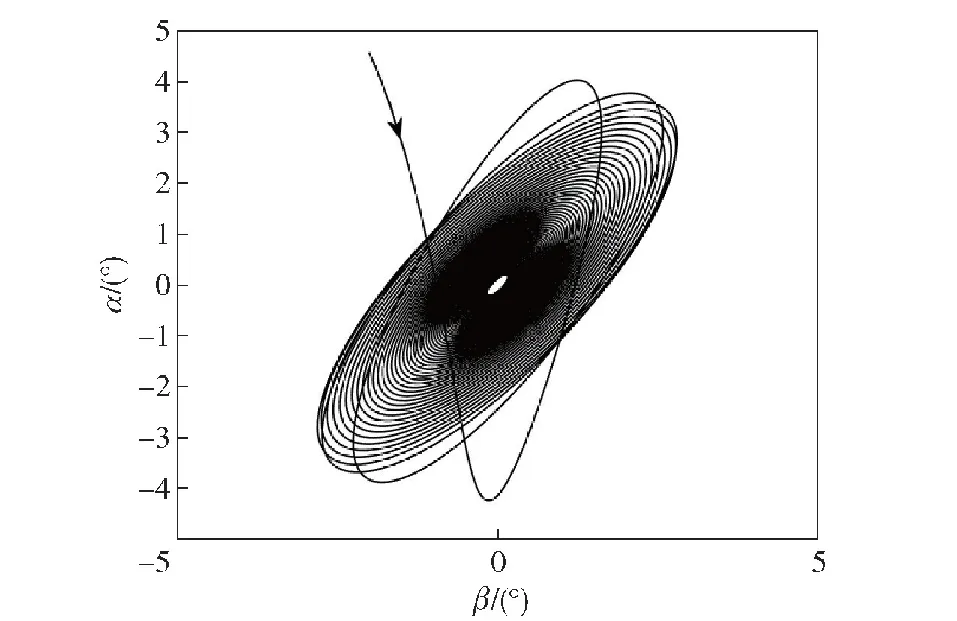
图13 λg=3°、kf=1.004时收敛的锥形运动Fig.13 Convergent coning motion with λg=3°、kf=1.004
当kc=475.6时,弹体锥形运动处于临界稳定状态,此时复攻角等幅振荡,如图14所示。图15给出了kc=490时复攻角的变化情况,此时制导回路增益kc大于稳定上限,锥形运动发散。
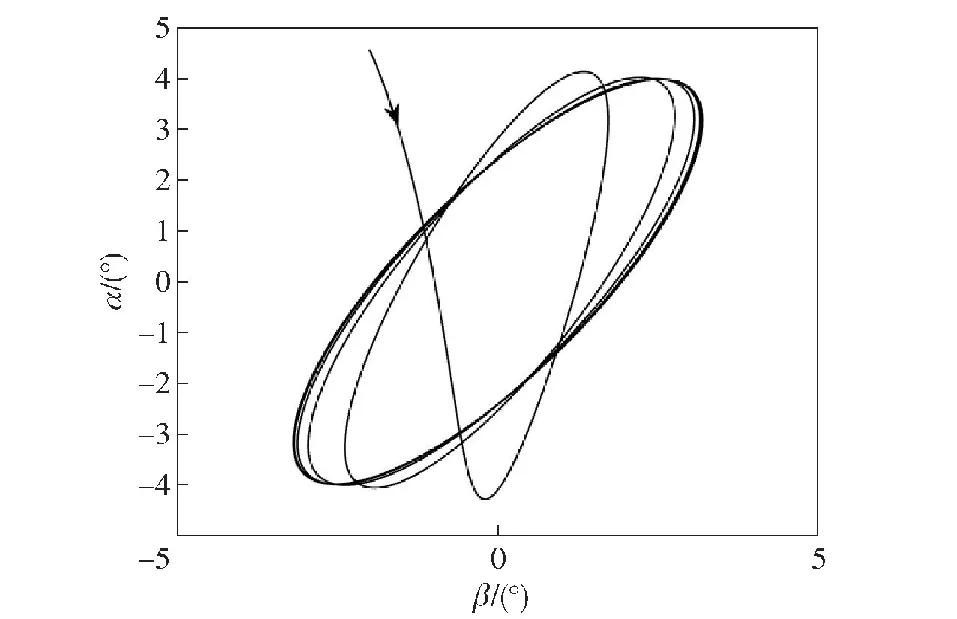
图14 λg=3°、kf=1.004时临界稳定的锥形运动Fig.14 Critical stable coning motion with λg=3°、kf=1.004
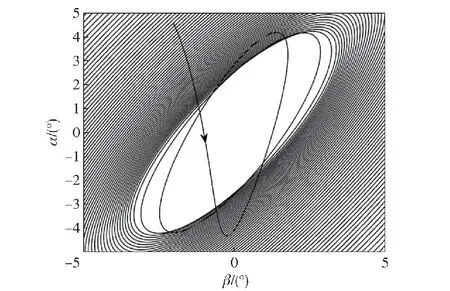
图15 λg=3°、kf=1.004时发散的锥形运动Fig.15 Divergent coning motion with λg=3°、kf=1.004
选取导引头延迟角λg=6°,弹体转速p=8π rad/s,阻尼回路增益kω=0.1,陀螺标度因数误差kf=0.996。图16给出了kc=190时弹体复攻角ξ=β+iα的变化情况,此时kc满足系统动态稳定性条件,可观察到该锥形运动收敛。当kc=224.9时,弹体锥形运动处于临界稳定状态,此时复攻角等幅振荡,如图17所示。图18给出了kc=260时复攻角的变化情况,此时制导回路增益kc大于稳定上限,锥形运动出现发散。

图16 λg=6°、kf=0.996时收敛的锥形运动(kc=190)Fig.16 Convergent coning motion with λg=6°、kf=0.996
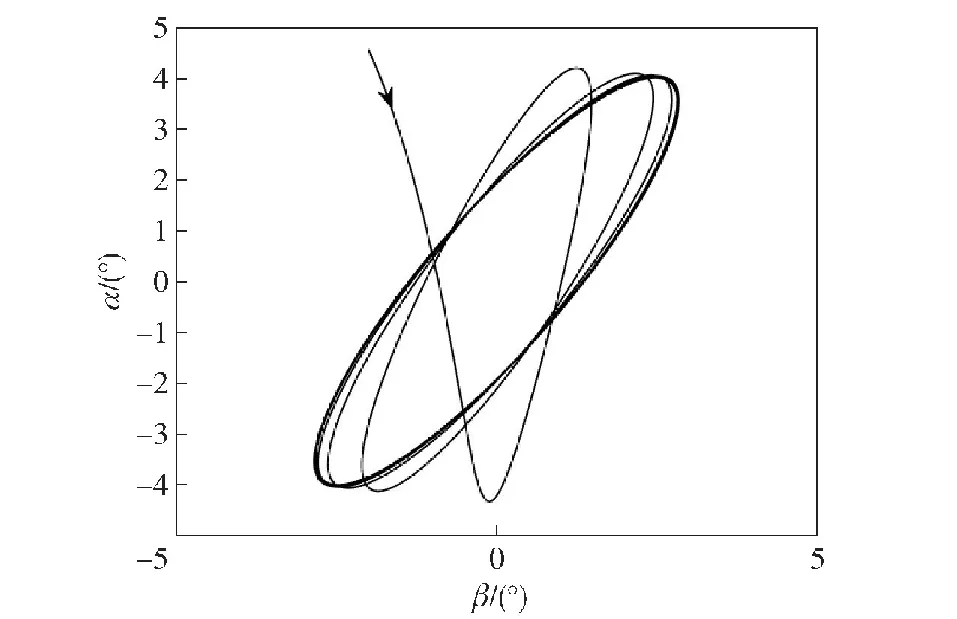
图17 λg=6°、kf=0.996时临界稳定的锥形运动Fig.17 Critical stable coning motion with λg=6°、kf=0.996
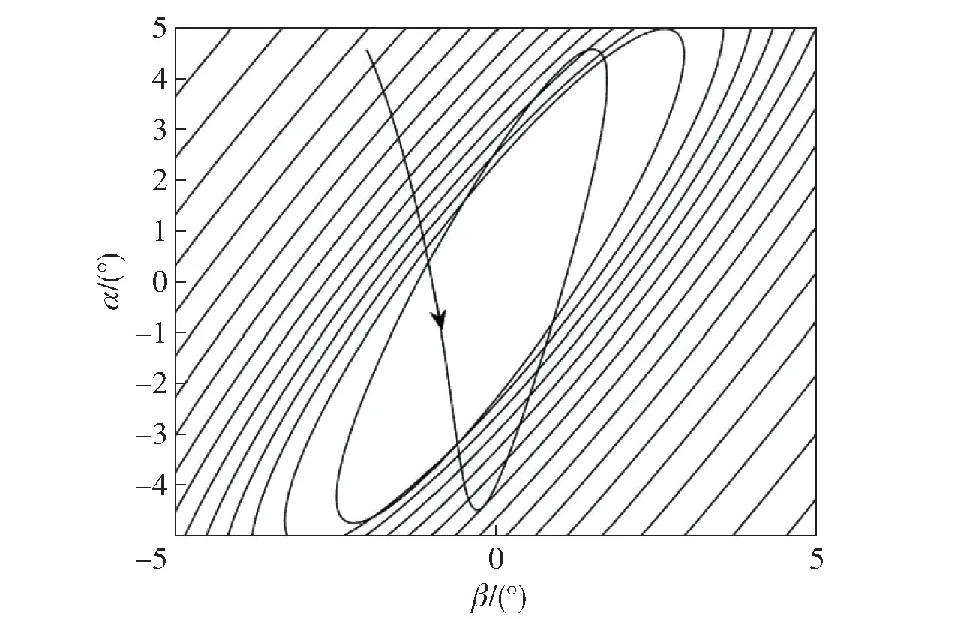
图18 λg=6°、kf=0.996时弹体发散的锥形运动Fig.18 Divergent coning motion with λg=6°、kf=0.996
根据仿真图12~图18可以看出,在不同的陀螺标度因数误差、弹体转速及阻尼回路增益下,数值解得的旋转弹稳定区域与仿真结果高度一致,同样证明了理论分析和数值解算方法的正确性。
4 结论
1) 本文针对采用捷联导引头和弹体追踪导引律的旋转弹,推导了捷联导引头在非旋转弹体坐标系中的动力学模型,并建立了复数形式的弹体追踪制导控制系统数学模型。
2) 考虑不同程度的导引头响应延迟,获得了不同弹体转速及阻尼回路增益下的旋转弹动态稳定区域,发现延迟角越大,使系统稳定的制导回路指令增益kc上限越小。
3) 考虑不同的陀螺标度因数误差,获得了不同弹体转速及阻尼回路增益下的旋转弹动态稳定性区域,发现标度因数误差系数大于1时,使系统稳定的制导回路指令增益kc上限会变大;标度因数误差系数小于1时,稳定上限会变小。

