基于被动相位噪声补偿的自由空间光学频率传递

仇子昂,胡 亮,周子杰,薛瑞旻,陈建平,吴龟灵

(上海交通大学区域光纤通信网与新型光通信系统国家重点实验室,上海 200240)

0 引言

时间是7个物理量中测量精度最高的一个物理量,精准的时间频率标准在射电天文学[1-2]、导航定位[3]、引力波探测[4]及基本物理量研究和测量[5]等多个领域中有着至关重要的作用。随着光学频率标准技术的逐渐成熟,光学原子钟的频率不稳定度可以达到10-19量级[6-7],相较于传统的原子钟的频率不稳定度提升了至少两个数量级。但是光学原子钟或离子钟体积大、系统复杂,对环境敏感,并且造价昂贵,不适用于大范围分布式应用。光学频率传递是推进该技术尽快实用的关键,它能使处于不同地理位置的用户共享同一高性能频率源。利用光纤本身具有的低损耗、抗电磁干扰等特性,以光纤作为传递链路的高精度光学频率传递得到了广泛的研究与应用[8-11]。虽然光纤的优良特性为大范围长距离多种信号同步提供了良好的通道,但是光纤链路仍然存在无法涉及的空间,虽然光纤的优良特性为大范围长距离多种信号同步提供了良好的通道,但是光纤链路仍然存在无法涉及的空间,比如可移动平台包括车地、星地、星间等,无法为“空-天-陆-海”提供全覆盖场景的高精度信号传输。

相比之下,自由空间光学频率传递不需要专门构建光纤链路,具有应用范围广、灵活性强等优点,适用于未来高精度导航、激光测距以及星地一体化等应用场景。然而,在自由空间的大气信道中,大气湍流、温度湿度波动以及天气等会影响光学频率传递的性能[12-13]。为了在接收端获得高精度的光学频率信号,需要在自由空间光学频率传递系统中使用相位噪声补偿技术来抑制传递链路引入的相位噪声。文献[14]中提出了一种基于主动相位噪声补偿方式的自由空间光学频率传递系统,通过不等臂迈克尔逊干涉仪探测激光信号在往返自由空间链路中引入的相位噪声,反馈给伺服控制系统来补偿前向的链路噪声。然而,由于伺服控制系统的锁定需要一定的时间,导致补偿速度有限。此外,自由空间链路中的光学频率信号容易受到大气湍流的影响剧烈波动,使得反馈信号幅度剧烈波动导致伺服控制系统失锁,经常需要人为地进行重新锁定。文献[15]利用二氧化硅集成的透镜辅助发射阵列实现了分布式光学频率传递,在接收端将单次通过的光与第三次通过的光拍频后进行二分频,即可在接收端被动补偿自由空间链路引起的相位噪声。该方案的优势在于采用芯片结合被动补偿方案,最大程度减少了系统的复杂度,但由于自由空间链路的衰减严重,第三次通过光的功率相对较小,因此该系统的最大传递距离有限。文献[16]通过两个站点中的光频梳利用线性光采样方式实现了自由空间的双向时间频率同步,能够有效修正两个站点之间的钟差,但光频梳设备较重且结构复杂,在实际应用过程中受限。

本文提出了一种在发射端进行被动相位噪声补偿的自由空间光学频率传递系统,仅使用混频和移频处理,不涉及闭环反馈回路,使得整体系统结构紧凑,成本低且易于实现。此外,在之前的工作中也证明了相较于主动相位噪声补偿技术,被动相位噪声补偿技术具有更快的补偿速度及相位恢复时间[17],适合自由空间光学频率传递。

1 被动补偿自由空间光学频率传递原理

1.1 系统结构

图1为发射端进行被动相位噪声补偿的自由空间光学频率传递系统原理图。在发射端,待传递的光学频率信号一部分通过法拉第反射镜(Faraday mirror, FM)返回作为干涉仪的参考臂,另一部分光信号则经过负一级衍射的声光调制器(acousto-optic modulator, AOM)AOM1,通过发射天线将光学频率信号发射至自由空间链路,经过平面反射镜反射至位于接收端的接收天线中,经过正一级衍射的AOM2,最后到达接收端的FM,形成了干涉仪的传输臂。

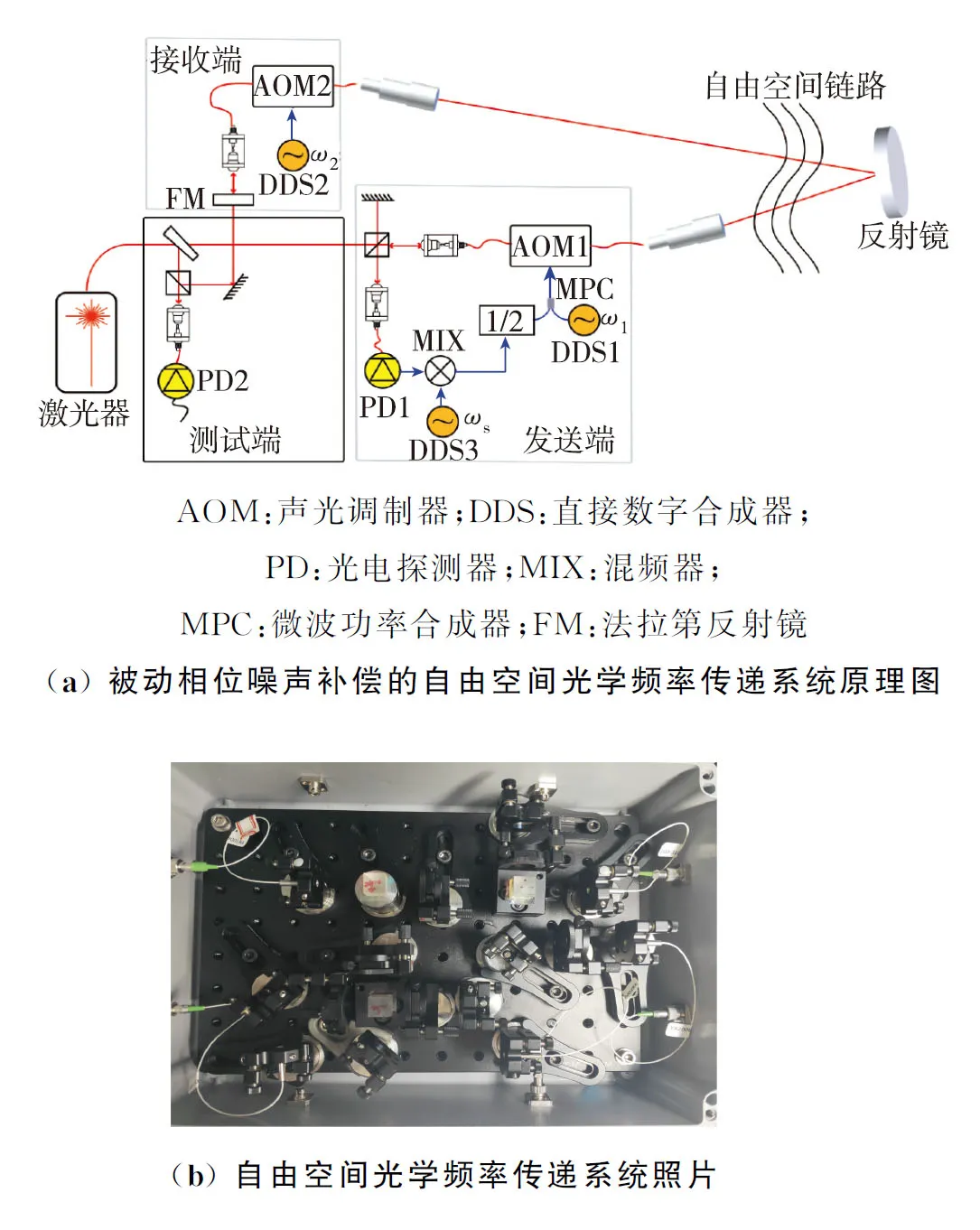
图1 基于被动相位噪声补偿的自由空间光学频率传递系统Fig.1 Free space optical frequency transfer system based on passive phase noise compensation

经过接收端FM返回的光信号与本地参考光在光电探测器(photo-detector, PD)PD1处拍频提取自由空间链路中引入的双倍相位噪声,在这里假设光信号在自由空间链路中前向和后向传输引入的相位噪声是相等的。PD1中提取的相位噪声信号经过一系列射频处理后反馈给发射端中的AOM1用于预补偿自由空间链路引入的相位噪声,而接收端的AOM2则用于区分和滤除传输过程中引入的杂散信号。经过发射端的相位预补偿后,在接收端即可获得相位稳定的光学频率信号。

1.2 相位噪声补偿过程

被动相位噪声补偿的具体工作原理如下。假设发射端待传递的光学频率信号的电场E0(t)可以表示为

E0(t)∝cos (ω0t+φ0)

(1)

其中,ω0和φ0分别表示待传递光学频率信号的角频率与初始相位。经过接收端的FM反射回到发射端的光信号的电场E1(t)可以写为

E1(t)∝cos[(ω0+2ω2-2ω1)t+φ0+2φp]

(2)

其中,ω1为驱动负一级衍射的AOM1的角频率,由直接数字合成器(direct digital synthesizer, DDS)DDS1产生;ω2为驱动正一级衍射的AOM2的角频率,由DDS2产生,且ω1>ω2。φp为由于环境扰动,在自由空间链路中引入的单向的相位噪声,且假设激光信号在前向传和后向传输时引入的相位噪声相等。因此,在发射端的PD1中将往返光信号与参考光信号进行外差拍频,得到的射频信号的电场E2(t)可以表示为

E2(t)∝cos[(2ω1-2ω2)t-2φp]

(3)

为了匹配AOM1的带宽,需要一个辅助射频信号与E2(t)信号利用混频器(Mixer, MIX)混频,滤出的下混频信号E3(t)可以表示为

E3(t)∝cos[(ωs-2ω1+2ω2)t+2φp]

(4)

其中,ωs为辅助射频信号的角频率,由DDS3产生。为了补偿光学频率信号在自由空间链路中引入的相位噪声,需要利用AOM1预补偿单向的相位噪声,对E3(t)二分频即可提取自由空间链路中引入的单向相位噪声,经过二分频后得到的射频信号的电场E4(t)可以写为

(5)

将E4(t)与角频率为ω1的射频信号经过微波功率合成器(microwave power combiner, MPC)后共同驱动AOM1,当E4(t)信号驱动负一级衍射的AOM1时便产生了带有链路共轭相位——φp的预补偿信号。经过这种被动补偿的方式,在接收端接收到的相位稳定的光学频率信号E5(t)可以表示为

(6)

从式(6)可以看出,在接收端获得了自由空间链路中引入的相位噪声被补偿的光学频率信号,仅需要简单的射频频率混合与分频的过程即可被动地补偿前向相位噪声。

2 实验设置及结果

2.1 实验设置

实验中采用的光学频率信号源为窄线宽激光器(NKT X15),波长约为1 550 nm,线宽约为100 Hz,输出功率约为13 dBm。AOM1和AOM2分别工作在负移频和正移频模式,相应的驱动频率分别设置为ω1=2π×75 MHz以及ω2=2π×45 MHz,辅助射频信号的角频率设置为ωs=2π×230 MHz。为了实现发射端和接收端之间的光束对准,发射端和接收端分别安装在两个独立的三维调整平台上,每个调整平台包括一个垂直平移平台、一个旋转平台和一个倾斜调整平台。在每个收发端装置上,光纤输出的光通过一个透镜进行准直,实验使用透镜的焦距为75 mm,通光孔径为25 mm,光束腰半径为7.4 mm。在实验过程中,通过调节反射镜的位置以改变传递距离,并进行了62 m以及150 m的室外自由空间光学频率传递的实验。对于150 m的自由空间链路,发射端的发射功率约为6.8 dBm,接收功率约为0.5 dBm,单程损耗约为12.5 dB。同时,每个终端均配备532 nm波长的对准光束用于辅助1 550 nm的待传递光信号对准。为了实验测试的便利,通过在自由空间链路的中间设置直径为20 cm的平面反射镜构成水平折叠链路以将发射端与接收端放置在同一站点。

为了评估被动补偿自由空间光学频率传递系统的稳定性,在发射端与接收端所处的站点设置了测试端。测试端中的PD2探测发射端的参考光信号与接收端接收到的光信号之间的拍频从而表征系统的稳定度。在上述实验配置下,驱动AOM1用于补偿单向相位噪声的射频信号的角频率为2π×85 MHz,因此,PD2探测得到的射频信号角频率为2π×40 MHz,使用门时间为1 s的无加权平均Π型频率计数器进行测量。

2.2 附加频率不稳定度测试结果

图2展示了自由空间链路在自由运转和稳定情况下的附加频率不稳定度以及传递系统的底噪和电底噪,根据频率计数器记录的∏型频率数据计算重叠阿伦偏差(overlapping Allan deviation, OADEV)来表征,实验结果表明,62 m自由空间链路在积分时间为1 s处的稳定度为7.2×10-17,并在平均时间1 000 s时下降到约2.9×10-19。同时,150 m自由空间链路在积分时间为1 s处的附加频率不稳定度为1.9×10-16,并在积分时间1 000 s时下降到约4.6×10-19。对于62 m的稳定自由空间链路,与自由运行时的频率不稳定度相比,利用被动相位噪声补偿技术的自由空间光学频率传递方案在千秒处能够有效地抑制自由空间链路噪声约3个数量级。

图2 被动相位噪声补偿的自由空间光学频率传递系统附加频率不稳定度测试结果Fig.2 Measured fractional frequency instability of the free space optical frequency transfer system with passive phase noise compensation

2.3 附加频率偏差评估

作为对表征系统频率不稳定度的阿伦方差的补充,通过分析参考输入光学频率信号以及输出的光学频率信号之间拍频信号来评估系统的附加频率偏差。图3(a)中绿色的点表示在连续7 000 s内使用门时间为1 s的Π型频率计数器记录的62 m稳定的自由空间链路的测试频率数据与期望频率之间的偏差,黑色的点表示对每40 s无周跳的连续时间内的175个数据点计算的无加权平均值。图3(b)和图3(c)分别绘制了稳定的62 m自由空间链路频率偏差的测试数据及其平均值的直方图(棕色柱状图)和高斯分布的拟合(红色曲线)。根据图3(c)中的结果,175个数据点的平均频率偏差以及标准差分别约为-24.36 μHz和463.38 μHz。假设这175个平均值点之间是相互独立的,则对应的光学频率信号的附加频率偏差约为1.81×10-19[18]。

图3 62 m自由空间链路传递所得的待传递光信号与稳定的输出信号之间拍频信号的偏差Fig.3 Measured beatnote deviation between input and stabilized output signal over the 62 m free space link

如图4所示,使用相同的分析方法,150 m传递链路,由频率计数器测得连续的4 760个Π型数据点的平均频率偏差约为10.45 μHz,将所有数据点平均分成119组,各组的无加权平均值计算得出的119个点的标准偏差约为823.75 μHz,对应的光学频率信号的附加频率偏差约为3.9×10-19。图4中具有较大偏差的点出现的原因在于测试时大气链路中的突然性波动。考虑到如图2所示的频率传输的长期稳定度,我们可以保守估计稳定的62 m和150 m的自由空间链路的相对频率偏差分别为2.9×10-19及4.6×10-19。综合附加频率不稳定度和附加频率偏差结果来看,该系统的性能能够满足目前先进的光钟光学频率传递和同步应用[19-21]。

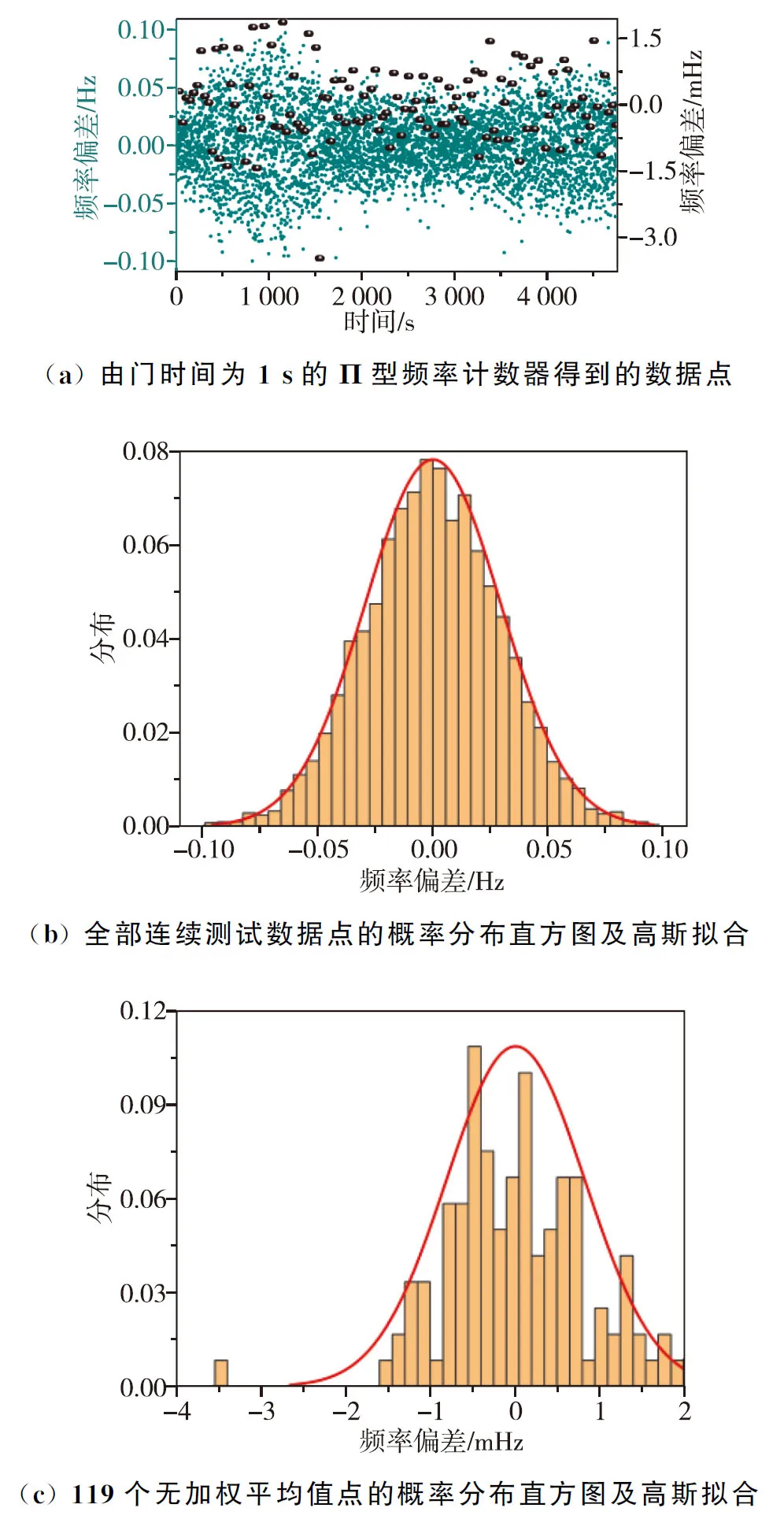
图4 150 m自由空间链路传递所得的待传递光信号与稳定的输出信号之间拍频信号的偏差Fig.4 Measured frequency beatnote deviation between input and stabilized output signal over the 150 m free space link

2.4 增加传递距离的方法

当光学频率信号在自由空间中进行传递时,会受到大气中的各种因素的影响如大气湍流、吸收和散射以及光束自身的发散等情况从而导致光功率的损耗。其中,大气湍流会根据自由空间中的不均匀的温度和压力等变化[22],考虑在晴朗天气下的光束由于光束发散、大气湍流、吸收和散射造成的传播损耗约为14 dB/km[23],受制于系统光电探测器的精度,该系统支持的最大单程衰减约为30 dB,估计在该系统的配置下最大传递距离可达到约1.4 km。采用放大倍数更大的光放大器可以增加传播距离,但会引入额外的放大器噪声。此外,增大收发装置中准直透镜的束腰半径也可进一步降低自由空间光学频率传递系统在发送和接收时的光功率损耗。如文献[21]中,发射端和接收端的光束腰半径约为20 mm,其传递距离可以延长至17 km。此外,由于大气湍流的影响,探测器的信号会发生中断,导致反馈系统无法实时补偿链路噪声,从而加大系统的频率不稳定度。一种有效的解决方法为采用卡尔曼滤波将中断信号进行预测恢复[24],但需要额外的控制电路,增加系统的复杂度。因此,长距离的自由空间光学频率传递的应用受限,有待进一步优化和改进。

3 结论

本文提出了一种基于发射端被动相位噪声补偿的自由空间光学频率传递系统。该系统结构简单,得到的光学频率不稳定度较低。对于150 m的自由空间链路,平均时间1 s的附加频率不稳定度约为1.9×10-16,平均时间1 000 s 的附加频率不稳定度约为4.6×10-19。在接收端得到的光学频率信号的附加频率偏差为10-19量级,稳定度能够满足光钟光学频率传递和同步的应用。相对于主动相位噪声补偿技术,该系统具备动态范围大、补偿速度快等特点,适用于自由空间光学频率传递,对于发展自由空间光时钟同步、卫星时频传递的发展具有重要意义。