韧性材料的冲蚀损伤数值仿真综述

张 开 ，唐振寰 ，王建方

（1.中国航空发动机集团有限公司，北京 100097；2.中国航发湖南动力机械研究所，湖南 株洲 412002）

0 引言

冲蚀是指在一定速度和尺度范围内松散的颗粒流过材料表面时，对材料表面造成的渐进性磨损现象[1]。韧性材料通常是指允许出现一定变形且不发生断裂的材料，例如金属或合金[2]。冲蚀是多相流动介质冲击材料表面造成的一种磨损现象，其中流动介质可以是气体也可以是液体。砂尘对韧性金属材料的冲蚀磨损现象广泛存在于石油天然气管道运输[3-5]、涡轮机械[6-7]、喷砂尘机械（sand blasting machine）[8]等诸多领域。例如飞机、高铁、汽车等交通工具在穿越多砂尘的地理环境时，空气中的砂尘极易对其金属零部件造成冲蚀损伤。此外，飞机在多砂环境工作时，空气中的砂尘不可避免会被吸入发动机[9]，随之与转子叶片发生碰撞，导致叶片产生严重的冲蚀磨损[10]，这会极大地破坏叶片结构完整性，有些情况下需要对叶片表面进行涂层防护[11-12]。

一般而言，依据不同的冲击条件，可以将冲蚀分为静态冲蚀和动态冲蚀。例如，自然风携带砂尘冲蚀钢结构建筑，油气携带砂尘冲蚀运输管道内壁，金属加工工艺中的磨粒对材料的喷射加工（Abrasive Jet Machining，AJM），均属于静态冲蚀。而风力发电机叶片、直升机旋翼和涡轮机械转子叶片受砂尘冲蚀属于动态冲蚀。此外，按砂尘冲蚀速度的不同又可将冲蚀分为低速、中速和高速3 种。例如，在自然风或石油天然气运输等环境下，砂尘冲蚀速度通常在100 m/s以内，一般认为是低速冲蚀。而在涡轮机械中，高速旋转的叶片与砂尘发生碰撞时，冲蚀速度更高，一般认为是高速冲蚀。

砂尘以一定速度撞击材料表面时，其与材料之间必然发生能量交换。当砂尘传递至材料表面的能量大到足以使材料产生塑性变形时，材料表面会产生凹陷等损伤。Meng 等[13]系统研究了1957～1991 年各国学者在Wear 期刊发表的冲蚀理论时发现，当前各冲蚀理论均通过研究影响损伤的各项因素作为切入点来揭示韧性材料冲蚀机理。其中较为经典的冲蚀理论如：Finnie[14]提出的微切削模型，Hutchings 等[15-16]提出的小冲击角单颗粒冲蚀模型，Bitter[17-18]提出的变形磨损模型，Bellman[19]提出的锻压挤压模型，Jahamnir[20]提出的冲蚀脱层模型和Tilly[21]提出的二次冲蚀模型等。这些理论认为影响材料冲蚀损伤的主要因素包含：砂尘冲击速度和冲击角、砂尘形状、砂尘密度和尺寸、被冲击材料的硬度和塑性变形行为、失效准则等。当前，随着现阶段试验表征技术和数值仿真水平的不断提高，对于深入阐释冲蚀损伤机理的研究和更先进的理论正在不断更新迭代。

本文在介绍砂尘冲蚀韧性金属材料损伤机理的基础上，综述了用于砂尘冲蚀研究的数值仿真分析方法，以及影响砂尘冲蚀机理的主要因素及其研究内容，以对砂尘冲蚀仿真分析的研究现状形成较为系统的认识。

1 固体颗粒侵蚀机理

在论述砂尘对韧性材料的冲蚀机理时，通常从韧性材料的损伤模式出发来研究其冲蚀损伤机理。Finnie 等[14，22-23]提出了单颗粒冲蚀损伤的微切削理论，为后续许多单颗粒冲蚀损伤模型提供了主要的概念和假设。该理论认为韧性材料的冲蚀损伤是由刚性单颗粒以一定速度和角度对材料表面造成微切削进而引起材料逐渐从表面脱落的结果。

Hutchings 等[15-16]更细致地研究了小冲击角下单颗粒造成的冲击损伤，建立了小冲击角下单颗粒的冲蚀模型，该模型认为尖角颗粒冲击姿态对材料冲蚀损伤的机理有较大影响。Hutchings 用高速摄影机拍摄钢球及立方块在冲击角为30°时冲蚀软钢的情况，结果发现立方块除了有确定的冲蚀角外，其顶角所在位置也会影响材料冲蚀损伤结果。进一步研究发现假如采用前倾角来表示这种关系，那么不同的前倾角对材料表面的破坏也不同，因此Hutchings 认为前倾角和冲击角直接决定了颗粒的碰撞姿态。此外，该模型还表明颗粒对材料表面造成的损伤分为2 种：球粒的犁削和多角粒子的切削。Hutchings 也讨论了熔化引起冲蚀损伤的可能性，并提出冲蚀过程主要是力学作用的结果，热效应仅起辅助作用。

Bitter[17-18]基于赫兹接触理论和能量平衡方程提出了一种变形磨损理论。该理论认为在冲蚀过程中，材料产生的切削磨损和变形脱落磨损这2 种损伤机制是材料被移除的主要原因，且二者同时发生，效果叠加。Tilly[21]基于脆性磨粒颗粒提出了第2次冲蚀理论，结合高速摄影和电子显微方法研究了磨粒破碎对韧性材料冲蚀的影响，研究发现颗粒碎裂程度与粒度、速度及冲蚀角有关：当粒径和速度足够大时，颗粒的碎裂将导致第2 次冲蚀损伤；第2 次冲蚀损伤程度正比于颗粒的动能和破碎程度。Tilly 认为冲蚀损伤机制主要分为2 个阶段：（1）材料受颗粒冲击产生凹坑，凹坑周围形成材料堆积，若冲击能量足够，堆积物将被直接切除；（2）颗粒在冲击过程中破碎，碎屑将隆起的堆积物切除。

Bellman 和Levy 等[19]提出了韧性材料的宏观冲蚀机制，认为撞击表面的颗粒会形成浅坑和类似晶片状的堆积物，这些堆积物很容易被随后的颗粒撞击而与表面分离，韧性材料的宏观冲蚀机制如图1 所示。在砂尘冲蚀过程中，材料表面锻造加工和绝热剪切变形会使堆积物快速形成，一旦颗粒冲击参数稳定，则堆积物的形成效率和材料的冲蚀率会趋于恒定。

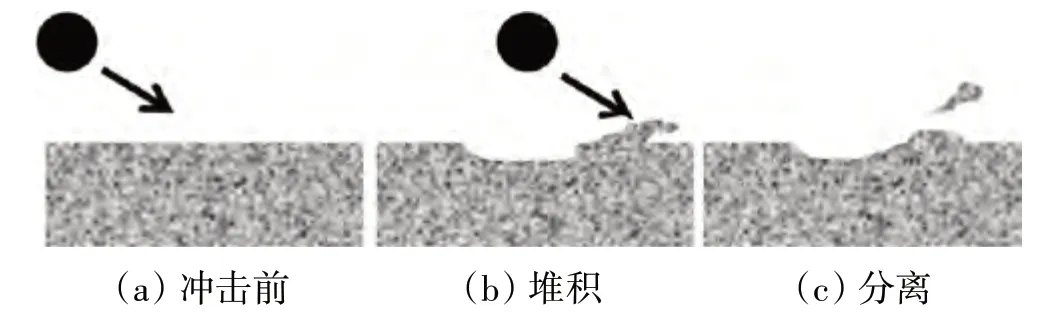
图1 韧性材料的宏观冲蚀机制[19]

Parsi 和Dong 等[24-25]对韧性材料的损伤机制进行了研究和总结，认为冲蚀过程中存在4 种不同的机制，分别是按压、犁削、切削和掀撬。当固体颗粒冲击参数满足一定条件时，材料表面将出现塑性变形，形成表面凹陷；当颗粒尖角刺入材料表面并沿着表面移动时发生犁削；切削是颗粒在小冲击角度下对撬开的材料造成切割的现象。在高速冲蚀领域，Li等[26]提出了3 种材料失效模式，即分别由惯性、伸长和绝热剪切带引起的失效。Li的研究结果表明，虽然凹坑的形成是由冲击位置附近的塑性变形引起的，但材料去除过程与韧性失效机理有关，这种机制不仅取决于塑性应变的大小，还取决于颗粒在凹坑表面高速滑动过程中产生的热条件。

2 砂尘冲蚀的数值模拟方法

砂尘与被冲蚀材料的接触时间极短，加之砂尘粒径微小，因此在现有的试验表征手段下，通过试验的方式观察不同条件下材料的破坏过程是极其困难的，而通过数值仿真可以较好地克服这一困难。Anwar等[27]采用有限元法（Finite Element Method，FEM）开展了喷水研磨中粒子的撞击过程仿真；Takafoli 等[28]使用光滑粒子流体动力学法研究了单粒子冲击韧性材料的材料变形和去除过程，并研究了带棱角固体颗粒冲击6061 铝合金的材料去除机制[29-30]；Hadavi 等[31]研究了碳化硅颗粒高速冲击铝合金的嵌入规律；Dong等[32]采用光滑颗粒流体动力学法模拟外来颗粒撞击表面侵蚀过程；Zheng 等[33]采用有限元法开展了多固体颗粒冲蚀Q345的数值仿真研究。数值仿真能较为清晰地观察单颗或多颗砂尘对材料冲蚀的影响，并且可以分析多种冲击条件作用下的协同效应，通过结合试验结果能更深入细致地揭示冲蚀机理。

2.1 有限元方法

FEM 能模拟材料任一位置的应力、应变随时间的变化规律[34]，因此能更清晰地观察砂尘冲击位置的损伤情况。采用有限元法研究冲蚀问题经历了由早期的2D 仿真到后来的3D 仿真的发展过程。2D 模型[35]具有网格精细和计算时间较短的优点，但必须服从某些假设，如平面应变、平面应力或轴对称模型假设，并且难以模拟多粒子冲蚀效应。3D 模型比2D 模型更接近真实情况[34]，Griffin 等[36]通过构建多颗砂尘连续冲击相同部位来近似模拟砂尘冲蚀条件，该模型进一步发展了3D仿真，使其能模拟实际材料的损失。随后有许多学者[37-39]尝试使用3D FEM 模型来研究砂尘冲蚀问题，多颗粒冲蚀的有限元仿真模型如图2 所示。但是，被冲蚀材料的网格容易在砂尘高速冲击时产生严重畸变，从而出现负体积效应而导致计算出现问题。当尖角砂尘高速冲击韧性金属材料时，材料的受冲击位置会产生局部较大变形，采用有限元法难以适应大变形条件下的求解。因此，Aquaro 等[40-41]尝试用拉格朗日-欧拉网格解决冲蚀过程中的局部大变形问题，但结果也不理想。

图2 多颗粒冲蚀的有限元仿真模型[33]

2.2 无网格方法

为适应砂尘冲击时材料出现的大变形情况，研究者大多采用无网格方法来建立冲击模型。无网格方法与FEM 相比最大的优势在于不会出现由网格畸变引起的网格缠结问题[42]。无网格方法大体分为无网格伽辽金法（Element-Free Galerkin，EFG）[43]、再生核粒子法（Reproducing Kernel Particle，RKP）[44]、单位分解法（Partition of Unity Method，PUM）[45]和光滑颗粒流体 动 力 学 法（ Smoothed Particle Hydrodynamics，SPH）[46]。在砂尘冲击建模中，主要应用的是EFG 和SPH。EFG 较适合砂尘等脆性颗粒的建模[47-48]，在模拟裂纹的萌生、扩展等方面有巨大优势。SPH 常用于构建靶板材料模型，采用SPH法建立的砂尘冲蚀模型如图3 所示。该方法能较好地模拟冲击过程中凹坑的形成以及凹坑周围材料堆积物大变形现象[29-31]。

图3 采用SPH法建立的砂尘冲蚀模型[29]

无网格方法的计算效率通常比FEM 低，为解决这一问题，多名学者先后提出了采用FEM 和无网格方法进行耦合建模的方法[49-51]，即在受砂尘冲击影响严重的区域使用无网格模型，而其余区域使用FEM模型。例如Wang 和Yang[42]开发了一种耦合有限元FEM 和光滑粒子流体动力学SPH 的模型（如图4 所示），研究了细微颗粒对Ti-6Al-4V 材料的冲击影响，其冲蚀率计算结果的趋势与Bitter[17-18]模型的趋势相似，说明该SPH计算方法具有较高的准确性。SPH能充分适应材料受砂尘冲蚀产生的塑性大变形现象，而FEM 能充分发挥计算效率高的特点，故该方法更适合冲蚀机理研究。SPH/FEM 耦合建模方法能较好地模拟材料受冲蚀产生变形的过程，在揭示细微颗粒冲蚀机理的方法上具有良好的应用前景。根据前文的分析，砂尘的破碎现象对材料的冲蚀损伤机理有较大影响，但遗憾的是，鲜有模型能在模拟材料大变形的同时，亦能考虑到砂尘破碎现象。

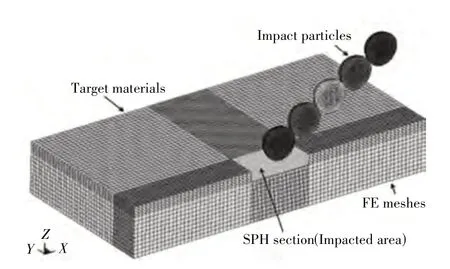
图4 FEM和SPH的耦合模型[42]

2.3 计算流体力学方法

许多学者[52-54]使用CFD 法预测砂尘在不同流动条件下的冲蚀率。基于CFD 的冲蚀计算程序通常由3 个步骤组成：（1）冲蚀区域流场计算；（2）粒子受力及运动计算；（3）粒子对靶板的冲击信息与材料的损伤关联。例如Giorgi 等[55]和Nguyen 等[56]分别对叶片和平板试验件开展了冲蚀仿真分析，连续冲蚀过程的CFD 模拟如图5 所示。由于在CFD 仿真中，难以将砂尘形状各异的性质通过模型建立起来，而且更重要的是，砂尘与材料均被视为不发生破碎和塑性变形的刚性体，因此仅仅依靠预测的冲击参数与冲蚀率之间的试验关系建立的CFD预测模型与真实试验环境相比具有较大差异。CFD计算的优势在于能较好地模拟冲蚀区域流场和颗粒冲击条件，但较难直接模拟颗粒对靶板的损伤过程，较难应用于冲蚀损伤机理的仿真研究。

图5 连续冲蚀过程的CFD模拟[56]

3 砂尘冲蚀数值模拟主要研究进展

材料受砂尘冲蚀损伤是逐颗砂尘依次冲击在材料表面产生损伤累积的结果，模拟单颗砂尘冲击材料的过程有助于理解冲蚀损伤的基本机制。在砂尘冲蚀研究领域，仿真的主要内容是通过建立确定性模型，分析砂尘冲击相关的各项因素对损伤的影响。

3.1 砂尘冲击速度和尺寸对冲蚀损伤的影响

在砂尘冲蚀过程中，砂尘冲击速度和尺寸对结果的影响比较独立，因此将二者一并综述。对于单颗砂尘的冲击而言，目前国内外研究人员[28，33，57]均比较认可的观点是随着冲击速度的增大，凹坑深度增加，损伤程度增大，但当冲击速度范围不同时，其结论有所不同。例如Zheng 等[33]通过建立圆形微小颗粒冲击Q235 平板的模型，发现随着冲击速度的增大，凹坑的深度和堆积物高度均增加，而颗粒与材料的接触时间却缩短了；Azimian等[38]研究了尖角颗粒在20～100 m/s的冲击速度范围内对C10100 铜合金的影响，发现在碰撞姿态不变的条件下，随着初始速度的增大，凹坑深度呈线性增加。文献[26，58]研究发现冲击速度相对较高时（350～700 m/s），凹坑的深度随冲击速度增大呈指数增加。通过对比分析发现，不同冲击速度的砂尘对材料造成损伤的严重程度存在明显差异。在高速条件下，在冲击过程中会产生较多热量，而产生的热效应会加速材料的软化，进而促进塑性变形的形成。

一般来说，冲蚀过程通常涉及2 个相互依存的阶段，即流体携带砂尘运动阶段和砂尘撞击阶段[59]。在先前的撞击阶段，流体对砂尘施加动能[60]，由于惯性力和阻力的差异，发现较小尺寸的砂尘响应更快，以致在撞击阶段其粒子的分布、轨迹和速度均出现差异[61]。Nguyen 等[62]研究了50～350 μm 不同粒径砂尘的冲蚀损伤情况，砂尘粒径对侵蚀结果的影响如图6所示。随着粒径的增大，凹坑剖面形状逐步从“W”形转变为“U”形，这是由于砂尘颗粒尺寸的变化导致粒子的轨迹、速度和冲击分布产生差异而导致的。颗粒尺寸越小证明其随流性越好[63]，但尺寸越小造成的损伤越小，大颗粒的砂尘是冲蚀损伤的主要来源[64]。Hadavi等[31]建立了粒径分别为219、363 μm 的砂尘对Al 6061-T6铝合金的冲击模型，为更好地模拟砂尘尖角对材料的穿刺破坏（embedment），针对Al 6061-T6铝合金平板采用SPH法建模。研究发现，在相同的冲击速度和冲击角度下，粒径较大的砂尘对材料的刺入深度是粒径较小者的1.79 倍，因此，在相同冲击条件下，更大的颗粒更有可能刺入材料表面，造成损伤也更严重。

图6 砂尘粒径对侵蚀结果的影响[62]

3.2 砂尘冲击姿态对冲蚀损伤的影响

砂尘形状、冲击角度和碰撞姿态等因素对损伤的影响存在一定的相互耦合关系。自然砂尘通常是一种带有尖角的颗粒，砂尘的冲击姿态取决于冲击角和方位角，而方位角与砂尘形状密切相关。Liu 等[65]分别模拟了立方体、十二面体、二十面体和圆球体以55 m/s 的速度和30°的冲击角冲击钛合金平板的情形，数值计算结果表明尖角粒子可以很好地预测小冲击角度下的冲蚀率，而球形和二十面体粒子可以很好地预测大冲击角的冲蚀率，二十面体颗粒的冲蚀率与整个冲击角范围内的试验结果吻合得很好，不同形状颗粒连续碰撞下归一化侵蚀率如图7 所示。从图中可见，砂尘模型的形状对冲蚀结果影响较大，而砂尘的形状又反过来影响砂尘的冲击姿态。

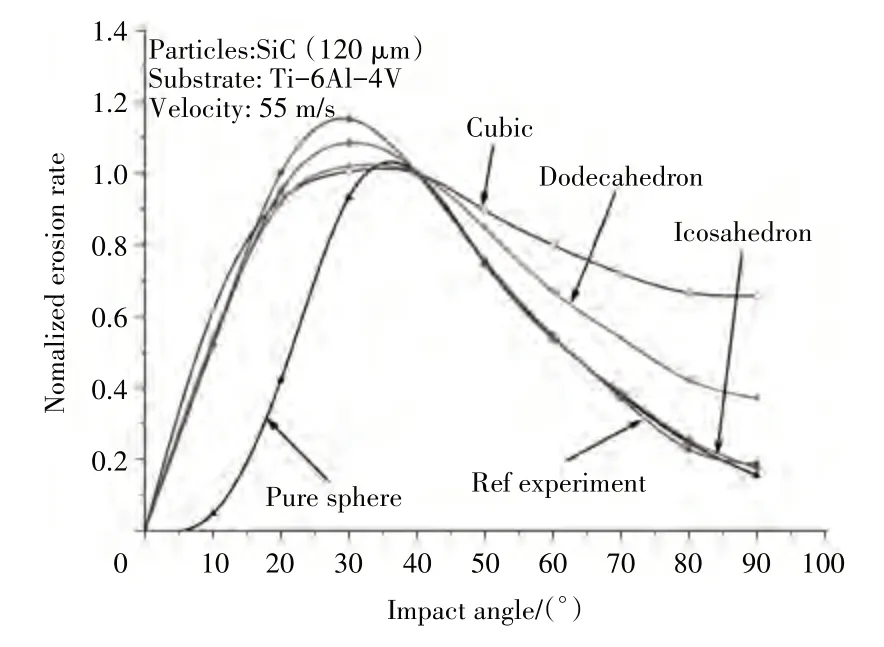
图7 不同形状颗粒连续碰撞下归一化侵蚀率[65]

Zheng 等[33]对砂尘在45°、90°冲击角度下的冲蚀进行了数值模拟，结果表明在45°冲击角度下冲蚀的凹坑呈现明显的剪切唇，具有不对称的特征；而在90°的冲击角度下，冲蚀的凹坑却是对称的。在确定砂尘方位角会对损伤机理产生影响的前提下，国内外学者随后对尖角颗粒的冲击角和方位角进行了更细致的研究。Azimian等[38]设置砂尘的冲击速度为81 m/s、方位角为20°并保持不变，而仅仅改变砂尘的冲击角，其变化范围为20°～80°，研究发现凹坑最大深度和容积随冲击角度的增大呈先增大再减小的趋势，在冲击角分别为70°、75°时取得最大值。此外的数值研究还发现，当冲击角和方位角之和≈90°时材料受损最为严重，砂尘的初始方位角θi和冲击角αi是影响冲蚀损伤程度的主要因素；对于给定的恒定冲击角αi，存在特定的方位角θs，使砂尘动能最大化地转换为材料内能；当θi＜θs时，粒子在与铜板碰撞后向前旋转，当θi＞θs时，粒子在撞击后向后旋转，前者更可能发生犁削损伤，后者更可能发生切削损伤。Hadavi 等[31]通过研究非规则尖角砂尘对材料嵌入影响发现，当冲击角一定时，方位角变化会使尖角颗粒不再刺入材料，该结果说明其方位角对损伤机理亦存在重大影响。Dong等[25，32]认为先前大多数研究集中于对称砂尘模型，其与真实砂尘形状相差较大。因此，为更加准确地表征砂尘形状，在建模过程中充分考虑了真实砂尘尖角的不规则性，使用SPH法模拟了更接近真实的尖角砂尘在方位角为-180°～180°条件下对韧性材料的影响，相同冲击角、不同方位角下材料损伤形态的部分计算结果如图8 所示。对于不规则形状的颗粒，其复杂性反映在动能损失与颗粒冲击姿态之间的关系中。此外，还发现砂尘碰撞姿态通过砂尘撞击时的前角、质心偏移角和撞击顶点角等3 个与形状相关的参数影响冲蚀机理，这3个参数随初始方位角θi的变化而变化。当θi从-180°～180°变化时，不规则形状砂尘撞击会导致犁削或切削变形的产生，从而导致动能损失随机变化。

图8 相同冲击角和不同方位角下材料损伤形态[25]

3.3 砂尘破碎对冲蚀损伤的影响

许多学者在冲蚀研究中均假设砂尘为刚体模型[25，29，32]而忽略砂尘在冲蚀过程中产生的破碎对材料损伤机制的影响。坚硬材料通常具有脆性较高的特点，目前，在脆性砂尘与金属壁面高速碰撞的研究中，已经有部分文献[47，66-67]提及了破碎现象。Tilly 和Sage[68]首次通过试验观察到脆性磨粒与金属碰撞导致的磨粒破碎现象，认为颗粒破裂成碎片可能会在初始冲击点周围区域形成二次损伤，从而开启了磨粒破碎对被冲蚀材料损伤影响的讨论。Murugesh 等[69]发现随着冲击速度与角度的增大，Al2O3砂尘的破碎率不断增大，这表明材料冲蚀率大小与砂尘的冲击动能和施加到靶板上的载荷大小有关。随后，Nahvi 等[70]也验证了该观点。Xu[71]尝试采用一种破碎理论模型来解释砂尘破碎与其自身所受应力和破裂能量的关系。Hadavi 等[47-48]采用EFG 法建立砂尘模型来研究SiC 砂尘冲蚀铝合金平板的破碎现象，冲击过程中的砂尘破碎现象如图9 所示。研究发现在靶板塑性变形和颗粒破碎过程中，颗粒大约会损失87%的初始动能，砂尘破碎过程会消耗部分能量，该现象恰好验证了磨粒的碎裂将在一定程度上影响冲蚀损伤。综上所述，当砂尘冲击碰撞时所受的应力高于破碎的临界值时，将出现破碎现象，而破碎需要耗散部分能量，因此，砂尘初始动能传递至被冲蚀材料上的能量将会比不考虑破碎情况时的更少。Murugesh 和Scattergood[69]开展了Al2O3和SiC 颗粒对不同硬度的氧化铝靶板的冲蚀研究，认为磨粒的自然尖角由于冲击断裂而钝化，进而改变材料的损伤机理。

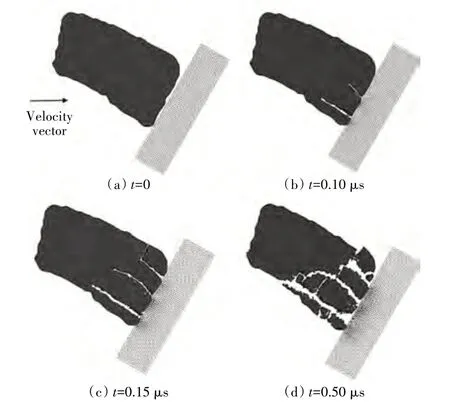
图9 冲击过程中的砂尘破碎现象[47]

3.4 靶板材料冲蚀损伤过程的数值模拟

Takaffoli 和Papini[28]通过采用SPH/FEM 耦合的仿真方法，观察了尖角颗粒分别在大、小冲击角下对材料动态响应的影响。在大冲击角下，材料受挤压破坏较多，在冲击凹坑周围形成材料堆积物；在较小的冲击角下，尖角颗粒逐渐将材料切除，仿真结果与试验结果相吻合。由于尖角颗粒并不是在较小的冲击角下就能产生微切削现象[45]，砂尘与靶板碰撞时的方位角也是影响材料损伤模式的重要因素[28，38]，因此通常在方位角与冲击角满足一定条件时，微切削现象才会发生。Dong[25]在仿真模型中保留了砂尘形状因子、尖角分布和质心位置等形状特征，以模拟真实颗粒对韧性材料的损伤。该模型通过改变砂尘的冲击姿态，重现了材料被切削、犁削、撬开、挤压等典型冲蚀损伤情况，采用SPH方法分析得到的典型冲蚀损伤模式如图10 所示。由此可知，砂尘对靶板造成的破坏模式通常可分为塑性挤压损伤和微切削损伤2大类型。

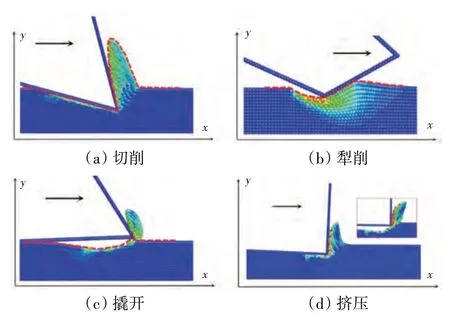
图10 采用SPH方法分析得到的典型冲蚀损伤模式[25]

不少学者[2，33，58]通过建立多颗砂尘模型来模拟连续冲蚀行为。Woytowitz 等[34]和ElTobgy 等[46]均建立了多个颗粒连续撞击的仿真模型，前者侧重对冲蚀损伤的空间和时间累积作近似模拟，后者侧重对冲蚀率结果进行预测。不足的是，上述模型忽略了后续砂尘与凹坑及其周围堆积物之间的相互作用。随后的一些文献[29，30，33]将后续颗粒对凹坑周围堆积物的影响纳入了数值模型的考虑范围。Zheng[33]通过模拟若干砂尘连续冲击相近位置观察了凹坑轮廓的几何演变，发现随着冲击次数的增加，变形区域扩大，特别在第4次碰撞之后，凹坑外部区域表现出严重的塑性变形，在连续碰撞之后，部分材料最终从靶板表面分离。Takaffoli 和Papini[29-30]研究了大量砂尘以不同姿态冲击靶板的损伤模式，发现在大多数情况下，砂尘冲击均会使材料表面产生凹坑，凹坑周围形成材料堆积，后续砂尘更容易将材料堆积物击打脱落，从而导致靶板出现材料损失，氧化铝粒子以速度117 m/s、30°冲击角碰撞靶板的过程如图11 所示。图中粒子从右向左射入，图11（a）中由于其他粒子撞击导致的额外弹坑并未显示。研究者认为这种现象才是砂尘在冲蚀过程中导致材料去除的主要原因。

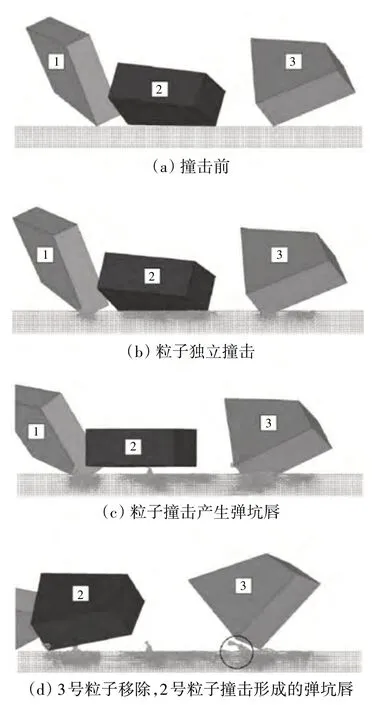
图11 氧化铝粒子以速度117 m/s、30°冲击角碰撞靶板的过程[29]

4 结束语

（1）砂尘对韧性材料造成的破坏模式通常分为材料凹陷、滑动、犁削和切削等4 种不同机制。当固体颗粒冲击参数满足一定条件时，材料表面在冲蚀作用下出现塑性变形，形成表面凹陷；当颗粒的尖角刺入材料表面并沿着表面移动时发生犁削；小冲击角度下对撬开的材料容易产生切削现象。

（2）当前国内外研究砂尘冲蚀损伤的数值仿真方法主要有有限元方法（FEM）、无网格方法（MM）和计算流体动力学方法（CFD）。FEM 计算效率高，但难以解决局部大变形问题；MM 适用于局部大变形情形，能较好地模拟冲蚀过程中材料产生的损伤；CFD难以模拟材料损伤过程，不适合用于冲蚀机理的研究。

（3）砂尘冲击姿态决定了材料的损伤模式。砂尘冲击姿态由冲击角和方位角共同决定，其中在小冲击角条件下，材料以切削损伤为主；而在大冲击角条件下，材料以挤压破坏为主。此外，当冲击角较小时，若方位角较小，则更可能出现犁削破坏。

（4）砂尘冲击速度和形状共同决定了材料的损伤程度。砂尘冲击速度不同，损伤呈现的增加趋势也不同。在较低的冲击速度下，随着初始速度的提高，材料凹坑深度呈线性增加。在较高的冲击速度条件下，材料凹坑深度呈指数形式增加。

（5）砂尘破碎现象对材料的去除机制有一定影响。在冲蚀过程中，砂尘破碎需要耗散部分能量，传递至材料表面的砂尘初始动能会有所降低。破碎后的砂尘碎屑在惯性作用下不可避免地会对材料表面造成二次冲蚀损伤。