含缺陷圆轴结构极限承载规律研究
龚小康,李翔宇,田占东,彭永
武器装备
含缺陷圆轴结构极限承载规律研究
龚小康,李翔宇,田占东,彭永
(国防科技大学 理学院,长沙 410073)
研究车辆传动轴在受损情况下极限承载能力的变化规律。在圆轴上预制缺陷,并对含缺陷圆轴结构承受扭转载荷的能力进行试验和数值模拟研究。当圆孔缺陷深径比保持不变时,圆轴极限扭矩下降比随圆孔缺陷孔径比的增加而减小;当圆孔缺陷孔径比保持不变时,圆轴极限扭矩下降比随圆孔缺陷深径比的增加而减小。当深径比大于0.4时,圆轴极限扭矩下降比与圆孔缺陷孔径比近似呈负线性相关。当缺陷孔径比大于0.4、深径比大于0.2时,圆轴最大扭角减小为15°~35°,各存在缺陷的圆轴的最大扭角差距不大。圆轴扭转失效时,其最大扭角、极限扭矩与圆孔缺陷孔径比、深径比整体均呈负相关趋势。在孔径比和深径比逐渐增大的过程中,极限扭矩呈近似线性关系逐渐降低,而最大扭角先急剧减小,后逐渐趋于平稳。
预制缺陷;极限扭矩;承载能力;传动轴;失效分析;数值模拟
车辆传动系统主要包括离合器、变速器、分动器、传动轴、万向传动装置、驱动桥等部件[1],其主要作用是将发动机输出的动力传递给驱动车轮,并实现减速增矩、变速变矩、倒车等功能。在传动系统中,从发动机至驱动桥之间的传动轴主要负责传递动力与转速,其在工作过程中主要承受扭矩作用。
车辆目标在战场上容易受到多种武器的打击,特别是轻武器和破片战斗部,这些武器对车辆目标的毁伤元主要是高速破片[2]。高速运动的破片在撞击到车辆时,会对车辆部件进行侵彻作用,从而造成部件一定程度的破坏。当车辆传动轴受到高速运动的破片侵彻作用时,破片会在命中处使传动轴产生一定深度和直径的孔洞缺陷。该孔洞缺陷的存在会使车辆传动轴的极限扭矩降低,甚至使得车辆传动轴在车辆运动过程中断裂,从而影响车辆的运动性能。因此,确定传动轴上缺陷对于传动轴极限承载能力的影响非常重要。
目前,国内外有很多学者针对不同工作环境下传动轴受力分析、有限元模型建立、断裂失效等相关情况进行了研究。LiShokrieh等[3]对玻璃纤维复合材料传动轴的固有频率进行的研究表明,当在传动轴上施加扭转载荷时,传动轴的扭转固有频率会下降,但弯曲固有频率不会受到影响。Asmamaw等[4]以玻璃纤维复合材料传动轴为研究对象,通过改变扭矩与临界转速分析传动轴的应力应变,结果表明,传动轴的扭矩与传动轴的扰度、应力应变之间存在线性关系。仲飞[5]采用边界元奇异积分方程的解析数值法,得到扭矩作用下任意截面柱边裂纹尖端的应力强度因子、应力场和柱体的抗扭刚度。李学光等[6]选用4节点常应变空间单元和8节点空间实体单元,建立了某型车辆主传动轴的有限元分析模型,运用瞬态动力学分析方法对该型车辆主传动轴加载后的动态响应进行了仿真,分析得出轴颈是主传动轴容易发生断裂的危险位置。刘文伟等[7]提出了先运用有限元结构振动方程确定汽车传动轴的机械变形量,再确定标定工况失效分析边界条件的基于有限元法的汽车传动轴机械断裂失效分析方法。运用有限元分析软件对传动轴结构进行数值建模,并对传动轴受力过程进行数值模拟分析,以及运用后处理技术对数值分析结果进行图形描述,成为众多学者对传动轴结构进行失效分析使用的一种方法[8-13]。
李玉婕等[14]对重型货车双后桥传动轴的扭转断裂进行分析,得到其断裂原因与原材料质量、热处理工艺、微观组织以及结构形状有关。樊世亮等[15]对断口采用宏微观分析、能谱分析、硬度检测等手段,得到断口尖角与中部出现夹杂物,淬硬层表层存在软化区,淬硬层浅表的硬度不达标,断口外层存在Ca、Mg、Al的夹杂物,断口纵截面的严重带状组织等因素是引发半轴脆性断裂的原因。李洪波等[16]对过滤器传动轴发生的失效现象进行了分析,确认传动轴材料强度过高、结构设计不合理、制造工艺不当可导致传动轴发生低应力断裂失效。金业全等[17]采用SEM形貌和EDS能谱分析等手段对某减速器传动轴进行了断裂失效分析,结果表明,传动轴表面缺陷处存在严重的应力集中,运行时引起疲劳裂纹的萌生及拓展,最终造成传动轴的断裂。吴梦雪等[18]采用数值模拟的方法建立了三维蚀坑模型来探讨蚀坑的长宽深对应力集中的影响,结果表明,高强钢丝应力集中系数会随蚀坑深宽比或宽深比的增加而增加,而随蚀坑长度的增加而减小。还有一些学者[19-25]采用力学性能分析、化学成分检测和金相分析等方法对机构传动轴断裂样品进行了全面分析,结果表明,键槽端部圆弧半径太小、阶梯轴处过渡圆角设计过小容易造成局部应力集中,当运行载荷较高时,会引起疲劳失效。
然而目前国内外对于传动轴的研究多在于材料失效和相关力学性能等方面,而对于其结构受损对承载能力影响规律的研究鲜有报道。为了建立传动轴上缺陷尺寸参数与传动轴极限承载能力之间的关系,本文将采用在圆轴上预制不同尺寸圆孔缺陷的方法研究圆孔缺陷直径、深度对圆轴极限承载能力的影响。
1 预制圆孔缺陷的圆轴承载试验
1.1 实验装置
高速运动的破片侵彻传动轴时,破片一般会在命中处使传动轴产生一定深度和直径的圆孔。为了分析破片打击后圆轴的极限承载能力,通过在圆轴上预制不同尺寸的圆孔来模拟破片打击下圆轴的受损程度。试验设备采用ETT系列扭转试验机,其扭矩测量范围为0~500 N·m,扭矩测量精度为0.000 1 N·m;转角测量范围为0°~1 000°,测量精度为0.000 1°。结合《金属材料室温扭转试验方法》[26]以及扭力试验机夹具设计圆轴试样。试样材料为42CrMo,整体采用随炉加热至850 ℃,保温3 h,出炉油冷至室温,再加热至560 ℃,回火2.5 h,出炉水冷至室温的淬火加高温回火的方式进行调质处理。制成标距尺寸为10 mm×100 mm的试样,并在试样中间钻孔,孔径为6 mm,孔深分别取0、2、4、6、8、10、2+2 mm(表示在试样上钻2个孔深为2 mm的孔),不同孔深的试样分别编号为①、②、③、④、⑤、⑥、⑦。
试验过程中,采用逐级加载法对试样施加扭矩。试样屈服前扭转速度设定为15 (°)/min,试样屈服后逐级增加扭转速度到600 (°)/min,之后保持扭转速度为600 (°)/min直至圆轴试样断裂。记录试样扭转过程中的极限扭矩和断裂时的最大扭角,同一工况试样重复试验3次。试验现场布局和典型试样如图1所示。
1.2 试验结果
各试样扭转试验后失效样品结果如图2所示。观察试验过程及各试样扭转结果,各圆轴试样扭转失效时,只有无缺陷等值圆轴瞬间断裂,且断裂面比较光整。说明等值圆轴断裂时,断裂面上各点应力同时达到材料的剪切极限。含缺陷试样失效时,发生变形的位置均处于缺陷处,说明圆轴缺陷处会受应力集中效应的影响。试验记录不同工况下试样极限扭矩和最大扭角见表1和表2。

图1 试验现场布局和试样

图2 φ10 mm×100 mm不同孔深圆轴试样扭转失效结果
表1 不同工况试样的极限扭矩
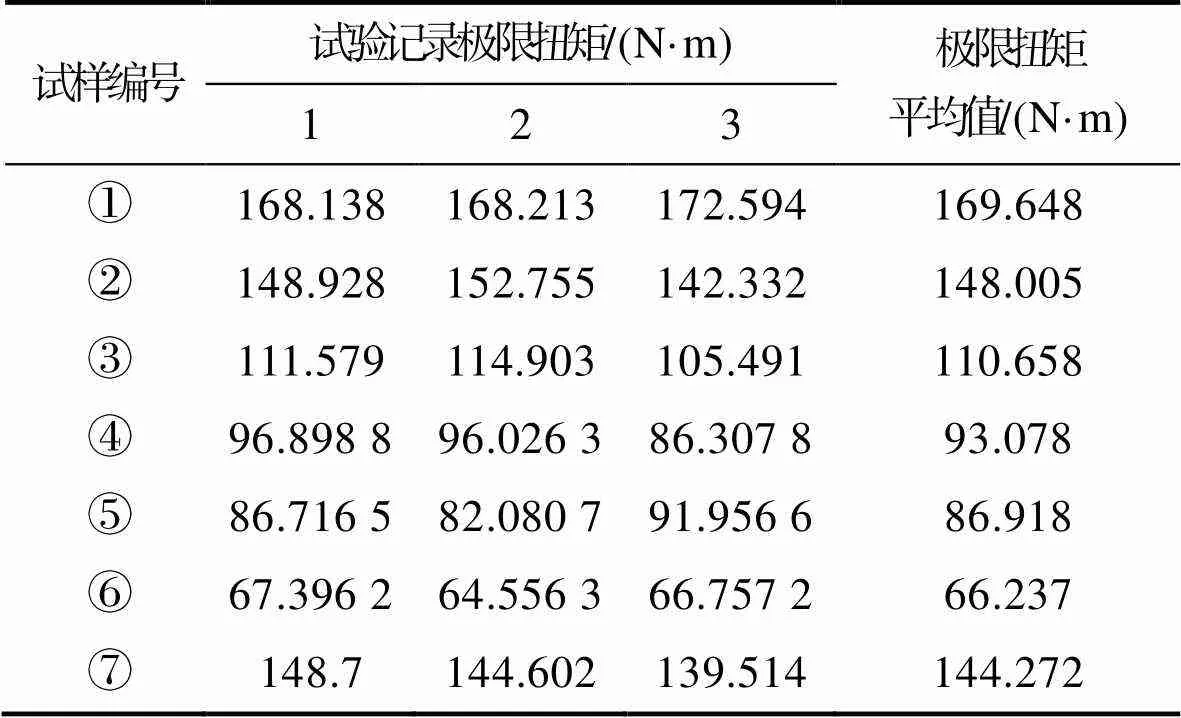
Tab.1 Ultimate torque of samples under different working conditions
表2 不同工况试样的最大扭角
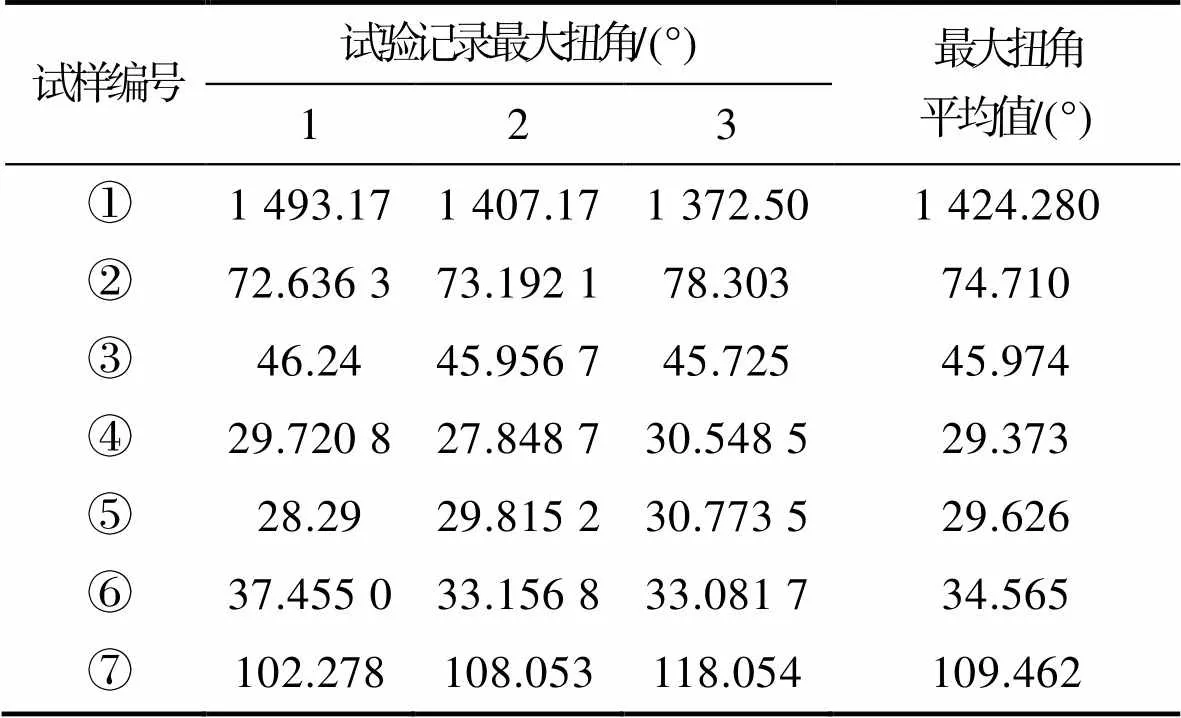
Tab.2 Maximum torsion angle of samples under different working conditions
观察表1和表2可知,对应于6 mm直径的圆孔缺陷,孔深尺寸与极限扭矩呈近似负线性相关。该圆轴试样中心被击穿一个6 mm孔径时,其能承受的极限扭矩从无缺陷时的169.648 N·m降低至66.237 N·m,约降为原来的39.04%。存在缺陷的圆轴扭转失效时,其最大扭角相较于无缺陷圆轴明显减小。当试样上6 mm孔径缺陷深度大于2 mm时,其扭转失效时的最大扭角减小为该圆轴无缺陷时的2%~8%。当轴上存在2个圆孔缺陷时,其能承受极限扭矩大小与只存在其中一个最大直径圆孔时接近。
2 数值模拟方法验证
2.1 计算模型
采用solid单元建立的圆轴有限元模型如图3所示。圆轴轴身平行于轴,两端头部设定为刚体,中间平行部分采用*MAT_PLASTIC_KINEMATIC模型,材料参数见表3。其中右端边界面施加*BOUNDARY_SPC边界条件,限制、轴向位移和、、旋转位移,左端施加*BOUNDARY_ PRESCRIBED_MOTION_RIGID边界条件,保持设定旋转速度。

图3 圆轴有限元模型
表3 圆轴中间平行部分材料参数

Tab.3 Material parameters of middle part of circular shaft
2.2 模型验证
采用上述模型计算10 mm×100 mm圆轴的①—⑦号工况,得到了6种工况的极限扭矩和最大扭角。②号工况试验与仿真所得扭角–扭矩变化曲线如图4所示。对比试验数据(表1和表2),绘制仿真结果与试验结果数据对比图,如图5所示。可以看出,仿真结果与试验结果吻合较好,表明该有限元模型可以有效地对预制缺陷圆轴扭转试验进行仿真计算。
3 结果分析
3.1 设计工况
为了研究圆轴直径、圆孔直径、圆孔深度在不同尺寸情况下极限扭矩max和最大扭角的变化情况,定义圆孔缺陷的孔径比为圆孔直径与圆轴直径的比值,定义圆孔缺陷的孔深比为圆孔深度与圆轴直径的比值,定义极限扭矩下降比为圆轴存在缺陷时的极限扭矩max1与该圆轴完整无缺陷时的极限扭矩max的比值。通过计算所得结果,分析圆孔缺陷的孔径比、孔深比对圆轴受纯扭转作用时极限扭矩下降比和最大扭角的影响。根据调整圆孔直径、圆孔深度和圆轴直径、圆轴长度等参数设计试样,不同工况试样的尺寸参数见表4。

图4 ②号工况试验与仿真计算所得扭角–扭矩对比

图5 ①—⑥号工况仿真计算结果与试验结果数据对比
表4 数值仿真不同工况试样参数

Tab.4 Sample parameters under different working conditions for numerical simulation
3.2 圆孔缺陷孔径比对圆轴极限扭矩和最大扭角的影响
研究孔径比对极限扭矩和最大扭角的影响,控制圆孔缺陷的深径比不变,设置2种不同尺寸圆轴来验证变化规律。使圆轴上圆孔缺陷的深径比保持为0.2、0.4、0.6、0.8、1.0,不同工况圆轴极限扭矩下降比与圆孔缺陷孔径比的关系曲线如图6所示。

图6 圆轴极限扭矩下降比T与圆孔缺陷孔径比g的关系
分析图6可得,当圆孔缺陷深径比保持不变时,圆轴极限扭矩下降比随圆孔缺陷孔径比的增加而减小。当深径比大于0.4时,圆轴极限扭矩下降比与圆孔缺陷孔径比近似呈负线性相关。上述2种不同直径圆轴具有相同的变化关系,进一步验证了极限扭矩下降比随圆孔缺陷孔径比的变化规律。圆轴孔深比保持不变时,最大扭角与圆孔缺陷孔径比的关系如图7所示。
分析图7及结合试验过程可知,圆轴上存在圆孔缺陷时,圆轴扭转失效的最大扭角相较于无缺陷圆轴明显减小。当缺陷孔径比大于0.4时,圆轴最大扭角减小为15°~35°,各存在缺陷圆轴的最大扭角差距不大。上述2种不同直径圆轴具有相同的变化关系,进一步验证了最大扭角随圆孔缺陷孔径比的变化规律。
3.3 圆孔缺陷深径比对圆轴极限扭矩和最大扭角的影响
研究深径比对极限扭矩的影响,控制圆孔缺陷的孔径比不变,设置2种不同直径圆轴来验证变化规律。使圆轴上圆孔缺陷的孔径比保持为0.2、0.4、0.6、0.8,不同工况圆轴极限扭矩下降比与圆孔缺陷的深径比的关系曲线如图8所示。
分析图8可知,当圆孔缺陷孔径比保持不变时,圆轴极限扭矩下降比随圆孔缺陷深径比的增加而减小。上述2种不同直径圆轴具有相同的变化趋势,进一步验证了极限扭矩下降比随圆孔缺陷深径比的变化规律。圆轴孔径比保持不变时,最大扭角与圆孔缺陷深径比的关系如图9所示。
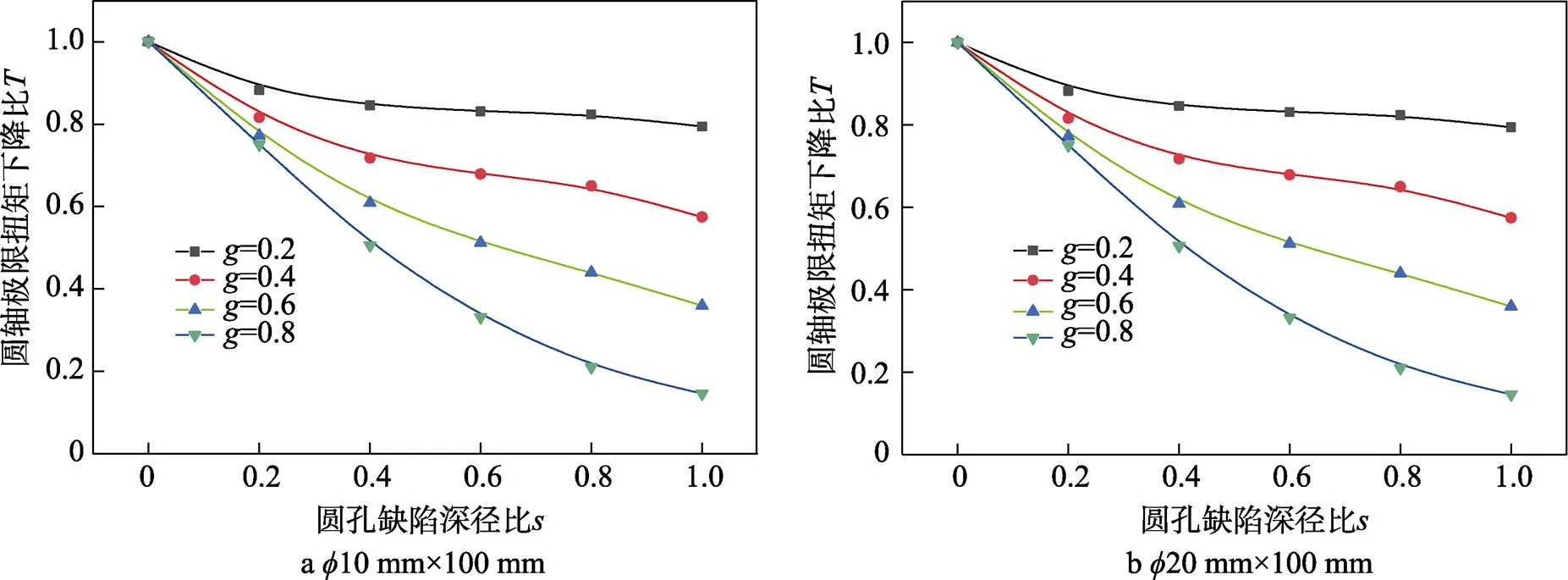
图8 圆轴极限扭矩下降比T与圆孔缺陷深径比s的关系

图9 圆轴最大扭角φ与圆孔缺陷深径比s的关系
分析图9及结合试验过程可知,圆孔缺陷孔径比不变,圆轴扭转失效时,其最大扭角与圆孔缺陷孔深比整体呈负相关的关系,缺陷孔深比从0增大至1的过程中,最大扭角先急剧减小而后逐渐趋于平稳。当孔深比和孔径比均大于0.4时,圆轴最大扭角减小为20°~30°,各存在缺陷圆轴的最大扭角差距不大。上述2种不同直径圆轴具有相同的变化关系,进一步验证了最大扭角随圆孔缺陷深径比的变化规律。
3.4 圆轴极限扭矩、最大扭角与圆孔缺陷孔径比、深径比的关系
为直观观察圆轴极限扭矩下降比、最大扭角随圆孔缺陷不同孔径比、深径比的变化情况,分别绘制极限扭矩下降比、最大扭角和深径比、孔径比之间的关系曲面,如图10和图11所示。由图10和图11可见,圆轴扭转失效时,其最大扭角、极限扭矩与圆孔缺陷孔径比、深径比整体均呈负相关趋势。在孔径比和深径比逐渐增大的过程中,极限扭矩呈近似线性关系逐渐降低,而最大扭角先急剧减小,而后逐渐趋于平稳。
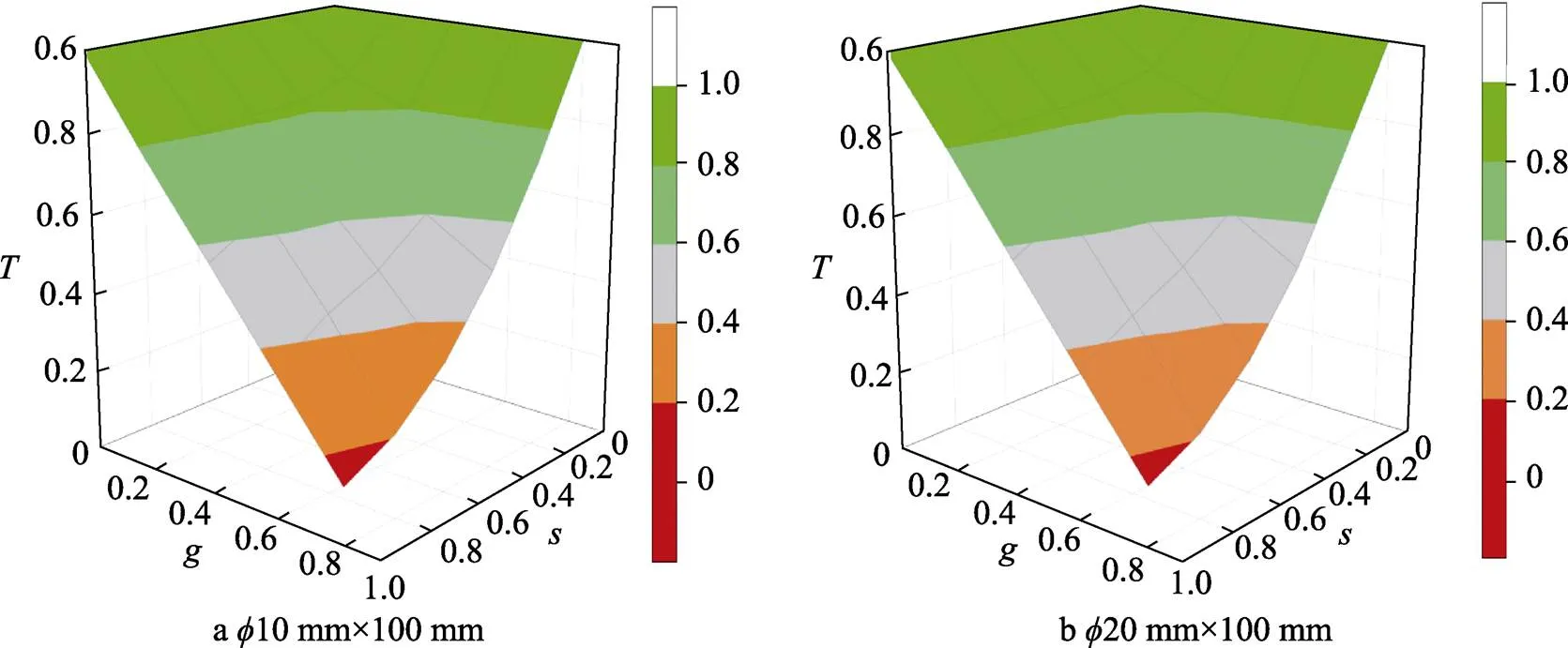
图10 圆轴极限扭矩下降比T与圆孔缺陷深径比s、孔径比g的关系
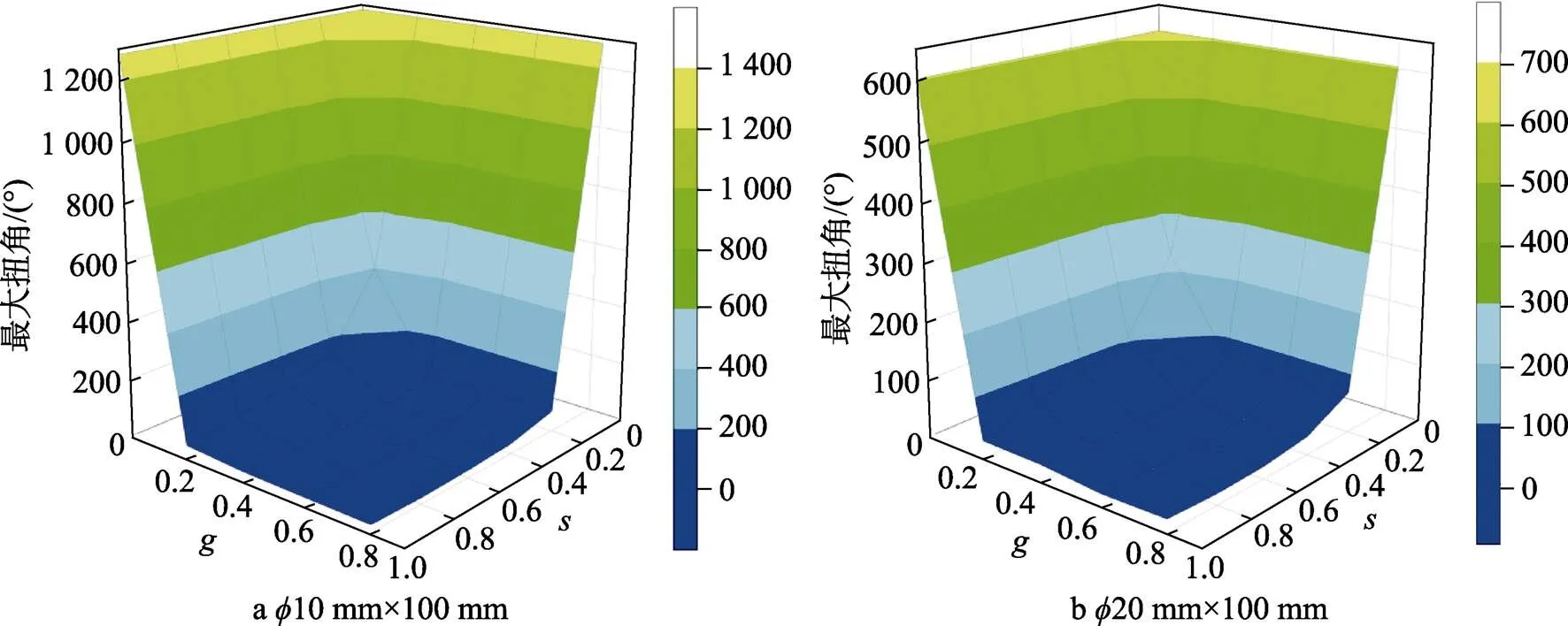
图11 圆轴最大扭角φ与圆孔缺陷深径比s、孔径比g的关系
4 结论
1)当圆孔缺陷孔径比保持不变时,圆轴极限扭矩下降比随圆孔缺陷深径比增加而减小;当圆孔缺陷深径比保持不变时,圆轴极限扭矩下降比随圆孔缺陷孔径比增加而减小。当深径比大于0.4时,圆轴极限扭矩下降比与圆孔缺陷孔径比近似呈负线性相关。
2)当圆轴上存在圆孔缺陷时,圆轴扭转失效时其最大扭角相较于无缺陷时圆轴最大扭角明显减小。当缺陷孔径比大于0.4、深径比大于0.2时,圆轴最大扭角减小为15°~35°,各存在缺陷的圆轴的最大扭角差距不大。
3)圆轴扭转失效时的最大扭角与圆孔缺陷深径比、孔径比整体呈负相关的关系,缺陷深径比从0增大至1的过程中,最大扭角先急剧减小而后逐渐趋于平稳。
[1] 刘仁鑫. 汽车构造与原理(下册)底盘车身[M]. 北京: 机械工业出版社, 2023.LIU Ren-xin. Automobile Structure and Principle(Volume II) Chassis Body[M]. Beijing: China Machine Press, 2023.
[2] (美) 陆军装备部. 终点弹道学原理[M]. 王维和, 李惠昌译. 北京: 国防工业出版社, 1988. [US]Army Armaments Department. Elements of Terminal Ballistics[M]. WANG Wei-He, LI Hui-chang Translated. Beijing: National Defense Industry Press, 1988.
[3] SHOKRIEH M M, HASANI A, LESSARD L B. Shear Buckling of a Composite Drive Shaft under Torsion[J]. Composite Structures, 2004, 64(1): 63-69.
[4] GEBRESILASSIE A. Design and Analysis of Composite Drive Shaft for Rear-Wheel Drive Engine[J]. International Journal of Scientific and Engineering Research, 2012, 3(5): 1-4.
[5] 仲飞. 带曲线边裂纹柱体的扭转断裂分析[D]. 青岛: 中国海洋大学, 2007. ZHONG Fei. Fracture Analysis for Torsion Problem of Bar with Curvilinear Edge Cracks[D]. Qingdao: Ocean University of China, 2007.
[6] 李学光, 张树仁, 苗立琴, 等. 基于扭力轴扭转断裂动力学分析研究[J]. 长春理工大学学报(自然科学版), 2010, 33(2): 68-70. LI Xue-guang, ZHANG Shu-ren, MIAO Li-qin, et al. Research on Torsion Dynamics Based on Torsion Bar’s Crack[J]. Journal of Changchun University of Science and Technology (Natural Science Edition), 2010, 33(2): 68-70.
[7] 刘文伟, 艾国, 白榕. 基于有限元法的汽车传动轴机械断裂失效分析[J]. 环境技术, 2019, 37(6): 158-162. LIU Wen-wei, AI Guo, BAI Rong. Mechanical Fracture Failure Analysis of Automobile Transmission Shaft Based on Finite Element Method[J]. Environmental Technology, 2019, 37(6): 158-162.
[8] 牟小燕. 基于ANSYS的碳纤维复合材料传动轴失效分析[J]. 内燃机与配件, 2018(21): 99-101. MU Xiao-yan. The Failure Analysis of Carbon Fiber Composite Material Transmission Shaft Based on ANSYS[J]. Internal Combustion Engine & Parts, 2018(21): 99-101.
[9] 聂文武, 肖雨, 毛洪海, 等. 某重型商用车传动轴强度与疲劳寿命分析[J]. 机械设计, 2018, 35(S1): 166-168. NIE Wen-wu, XIAO Yu, MAO Hong-hai, et al. Strength and Fatigue Analysis on Driving Shaft of Heavy Commercial Vehicle[J]. Journal of Machine Design, 2018, 35(S1): 166-168.
[10] 王凯, 叶年江. 基于ANSYS有限元的复合材料传动轴失效分析[J]. 科技创新导报, 2016, 13(5): 58-61. WANG Kai, YE Nian-jiang. Failure Analysis for Composite Propeller Shaft Based on ANSYS Finite Element[J]. Science and Technology Innovation Herald, 2016, 13(5): 58-61.
[11] 韩广. 分层缺陷对碳纤维复合材料传动轴扭转性能的影响研究[D]. 武汉: 武汉理工大学, 2020. HAN Guang. The Effect of Delamination Defects on the Torsional Performance of CFRP Drive Shaft[D]. Wuhan: Wuhan University of Technology, 2020.
[12] 李尚平, 叶才福, 张彪, 等. 甘蔗收获机分动箱传动轴失效的有限元分析[J]. 装备制造技术, 2016(7): 1-4. LI Shang-ping, YE Cai-fu, ZHANG Biao, et al. Finite Element Analysis of Failure Mechanism of Sugarcane Harvester Transfer Case Transmission Shaft[J]. Equipment Manufacturing Technology, 2016(7): 1-4.
[13] 李帅. 复合材料传动轴柔性补偿设计及其力学性能分析[D]. 哈尔滨: 哈尔滨工业大学, 2021. LI Shuai. Flexible Compensation Design and Mechanical Performance Analysis of Composite Transmission Shaft[D]. Harbin: Harbin Institute of Technology, 2021.
[14] 李玉婕, 阎野, 宋玉涛, 等. 重型货车双后桥传动轴扭转断裂的失效分析[J]. 热处理技术与装备, 2014, 35(4): 38-42. LI Yu-jie, YAN Ye, SONG Yu-tao, et al. Failure Analysis on Torsion Fracture of the Dual Rear Axle Shaft for Heavy Goods Vehicle[J]. Heat Treatment Technology and Equipment, 2014, 35(4): 38-42.
[15] 葛艺, 王琪, 高生祥, 等. 商用车42CrMo钢半轴扭转断裂失效分析[C]//2021年全国金属材料失效分析专题培训研讨会论文集. 上海: [出版者不详], 2021. FAN Shi-liang, GE Yi, WANG Qi, et al. Failure analysis of commercial vehicle 42CrMo Steel semi-shaft torsional fracture [C]//Proceedings of the 2021 National Training Seminar on Failure Analysis of Metal Materials. Shanghai: [s. n.], 2021.
[16] 李洪波, 侯宗宗, 张辉, 等. 压载水过滤器传动轴失效的分析[J]. 机械制造, 2022, 60(6): 80-82. LI Hong-bo, HOU Zong-zong, ZHANG Hui, et al. Failure Analysis of Transmission Shaft of Ballast Water Filter[J]. Machinery, 2022, 60(6): 80-82.
[17] 金业全, 刘俣. 减速器传动轴断裂失效分析[J]. 机车车辆工艺, 2021(3): 46-48. JIN Ye-quan, LIU Yu. Failure Analysis of the Transmission Shaft Fracture in a Reducer[J]. Locomotive & Rolling Stock Technology, 2021(3): 46-48.
[18] 吴梦雪, 尹力, 唐德发. 高强钢丝蚀坑尺寸对应力集中效应的影响[J]. 西南石油大学学报(自然科学版), 2021, 43(6): 62-70. WU Meng-xue, YIN Li, TANG De-fa. Influence of Corrosion Pit Size on Stress Concentration of High Strength Steel Wire[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2021, 43(6): 62-70.
[19] 李贵波, 马正伟. 行车减速机传动轴断裂的失效分析[J]. 山东冶金, 2022, 44(1): 81. LI Gui-bo, MA Zheng-wei. Fracture Failure Analysis of Transmission Shaft of Traveling Crane Reducer[J]. Shandong Metallurgy, 2022, 44(1): 81.
[20] 刘灿杰, 吕泮功, 窦小鹏, 等. 液压泵传动轴断裂失效分析[J]. 机械传动, 2018, 42(8): 129-132. LIU Can-jie, LYU Pan-gong, DOU Xiao-peng, et al. Fracture Failure Analysis of Hydraulic Pump Drive Shaft[J]. Journal of Mechanical Transmission, 2018, 42(8): 129-132.
[21] 白云岭. 等速传动轴断裂失效分析研究[D]. 上海: 上海交通大学, 2015. BAI Yun-ling. Research on Fracture Failure Analysis of the Outer Race of Drive Shaft[D]. Shanghai: Shanghai Jiao Tong University, 2015.
[22] 周薇, 曾会书. 传动轴断裂失效分析[J]. 热处理技术与装备, 2014, 35(3): 52-54. ZHOU Wei, ZENG Hui-shu. Failure Analysis on Fracture of Transmission Shaft[J]. Heat Treatment Technology and Equipment, 2014, 35(3): 52-54.
[23] 张建明, 宋斌. 传动轴失效分析[J]. 热处理技术与装备, 2011, 32(3): 57-59. ZHANG Jian-ming, SONG Bin. Failure Analysis of the Transmission Shaft[J]. Heat Treatment Technology and Equipment, 2011, 32(3): 57-59.
[24] 牛龙江, 张明友. 传动轴脆性断裂失效机制的研究[J]. 武汉工学院学报, 1994, 16(1): 53-58. NIU Long-jiang, ZHANG Ming-you. A Study of Mechanism of Tempering Embrittlement Fracture in Transmission Shafts[J]. Journal of Wuhan Institute of Technology, 1994, 16(1): 53-58.
[25] 王峥, 王放明, 谷阳阳, 等. 基于失效分析的汽车传动轴断裂的鉴定[J]. 汽车与安全, 2016(6): 95-99. WANG Zheng, WANG Fang-ming, GU Yang-yang, et al. Identification Based on the Failure Analysis of Automobile Transmission Shaft Fracture[J]. Auto & Safety, 2016(6): 95-99.
[26] GB/T 10128—2007, 金属材料室温扭转试验方法[S]. 北京: 中国标准出版社, 2008. GB/T 10128—2007, Metallic Materials—Torsion Test at Ambient Temperature[S].
Ultimate Bearing Law of Circular Shaft Structure with Defect
GONG Xiao-kang, LI Xiang-yu, TIAN Zhan-dong, PENG Yong
(College of Sciences, National University of Defense Technology, Changsha 410073, China)
The work aims to study the change rule of ultimate bearing capacity of damaged vehicle drive shafts. The defects were prefabricated on a circular shaft and the torsional load bearing capacity of the circular shaft structure with defects was investigated experimentally and numerically. The results showed that when the depth-diameter ratio of the circular hole defect remained unchanged, the decreasing ratio of ultimate torque of the circular shaft decreased with the increase of circular hole defect aperture ratio. The decreasing ratio of the ultimate torque of the circular shaft decreased with the increase of the depth-diameter ratio of the circular hole defect when the aperture ratio of the circular hole defect remained unchanged. When the depth-diameter ratio was greater than 0.4, the decreasing ratio of the ultimate torque of the circular shaft was approximately negatively linear correlated with the aperture ratio of the circular hole defect. When the defect aperture ratio was greater than 0.4 and the depth-diameter ratio was greater than 0.2, the maximum torsion angle of the circular shaft decreased to between 15° and 35°, and there was little difference in the maximum torsion angle between the circular shaft with defects. When torsional failure occurs, the maximum torsion angle and ultimate torque of the circular shaft are negatively correlated with the aperture ratio and the depth-diameter ratio of the circular hole defect. In the process of increasing aperture ratio and depth-diameter ratio, the limiting torque decreases gradually in an approximate linear relationship, while the maximum torsion angle decreases sharply at first and then gradually becomes stable.
prefabrication defect; ultimate torque; bearing capacity; drive shaft; failure analysis; numerical simulation
2022-09-15;
2022-10-09
GONG Xiao-kang (1998- ), Male, Postgraduate.
李翔宇(1980—),男,博士。
LI Xiang-yu (1980- ), Male, Doctor.
龚小康, 李翔宇, 田占东, 等.含缺陷圆轴结构极限承载规律研究[J]. 装备环境工程, 2023, 20(6): 001-009.
TB121
A
1672-9242(2023)06-0001-09
10.7643/ issn.1672-9242.2023.06.001
2022–09–15;
2022–10–09
国家自然科学基金(12172380)
Fund:The National Natural Science Foundation of China (12172380)
龚小康(1998—),男,硕士研究生。
GONG Xiao-kang, LI Xiang-yu, TIAN Zhan-dong, et al.Ultimate Bearing Law of Circular Shaft Structure with Defect[J]. Equipment Environmental Engineering, 2023, 20(6): 001-009.
责任编辑:刘世忠

