基于离散元法的钢轨力学性能定性分析

陈宪麦，陈楠，魏子龙，杨飞，尤明熙

(1. 中南大学 土木工程学院，湖南 长沙，410075；2. 重载铁路工程结构教育部重点实验室，湖南 长沙，410075；3. 中国铁道科学研究院集团有限公司 基础设施检测研究所，北京，100081)

近年来，重载铁路、高速铁路迅速发展，年运量和列车运行频次也不断提高。钢轨作为轨道结构的重要组成部分，其功能主要是引导列车车轮前进，将承受的荷载传至轨枕，有时还兼有轨道电路的功能。随着列车荷载的往复作用，钢轨上逐渐出现裂纹、轨头核伤、轨头压溃、轨头剥离、折断等病害[1-3]。这些不同程度的钢轨伤损将会影响旅客的舒适性和列车运行的安全性，也会影响轮轨接触，产生更大的轮轨作用力，进一步增大钢轨裂纹、折断等伤损的可能性[4-5]。为了了解钢轨的性能，许多研究人员对钢轨进行了探究。马晓川等[6]运用近场动力学损伤理论研究了钢轨裂纹的萌生和发展规律，得出萌生于钢轨轨头的裂纹启裂于钢轨表面下约2 mm处；HU等[7]对不同硬度的钢轨磨耗情况进行了研究，分析了体积硬度、试验后硬度、硬化率等对钢轨磨损率的影响；胡文博等[8]采用深度学习方法对钢轨的伤损进行了探测，并对钢轨不同位置的伤损进行了分类；GUI等[9]研究了微观结构对贝氏体钢轨的滚动接触疲劳性能的影响；ZHAO等[10]研究了钢轨表面的球形凹痕对其微观结构和滚动接触的影响；PAN 等[11]研究了钢材的微观结构对其服役性能的影响，指出钢材的使用寿命受微观结构的影响很大。

从宏观层面考虑，钢轨属于连续体，可以用有限元方法进行模拟[12-15]，这也是钢轨常用的数值模拟方式。有限元模型假设钢轨是一个各向同性的连续体，采用有限元法可以模拟钢轨在不同列车荷载作用下的受力情况，根据材料的属性，当应力达到钢轨屈服强度时，该处的应力不再增大，增加的荷载由其余未达到屈服强度的区域承担。而实际上，钢轨是由许多微细观颗粒组成的，当钢轨承受的荷载较大时，在其内部会产生细小裂纹，这些裂纹会随着外部荷载的增加而扩展，采用有限元模型无法模拟钢轨内部裂纹的扩展情况。为此，本文采用离散元法，将细小的颗粒通过平行黏结组成钢轨，并根据钢轨的力学性能对细小颗粒添加接触模型和相关的力学参数。当离散元模型钢轨承受的荷载超过屈服强度时，颗粒之间的接触力链会发生断裂，从而产生裂纹，这些裂纹会随着车轮垂向位移的增大而不断发展，直至钢轨失效。

对于钢轨微观性能的研究，已有学者运用元胞自动机的方法探究钢轨和车轮之间的磨损及其演变规律[16]，但是没有考虑钢轨内部的损伤机理。元胞自动机是一种时间和空间都离散的数值模拟方法，主要是以网格(包括三边、四边、六边网格)作为元胞单元，根据元胞的当前状态及其邻居状况确定下一时刻该元胞状态的动力学函数，下一步结果是以上一步结果为基础，可以预测复杂问题的发展趋势。而离散元法是一种在时间上连续、空间上离散的模拟方法，本文运用细小的球体颗粒作为模拟钢轨内部的小单元，通过对颗粒间施加平行黏结模型和黏结强度使其成为一个整体。本文拟构建基于离散元法的钢轨静力学分析模型，该模型由细小球体颗粒构成，并设置颗粒之间的接触模型和黏结强度，以保证模型与实际的钢轨性能接近，同时又可以从微观和细观的角度了解和分析钢轨内部的作用机理，对掌握和优化钢轨性能具有参考价值和指导意义。

1 钢轨离散元模型的建立

1.1 物理力学参数的选定

钢材由金相晶体构成，其内部的晶体结构主要分为体心立方体、面心立方体和密排六方体3种[17-18]。为了近似分析钢轨内部晶体之间的荷载传递和相互作用规律，通过离散元法模拟钢轨，采用小粒径(如1.0 mm)球体构建钢轨，用小粒径球体颗粒近似模拟钢材中的晶体晶粒，并设置颗粒之间的接触模型为平行黏结模型，近似模拟晶体晶粒之间的相互作用关系，以便于分析颗粒间的荷载传递情况。

现代钢轨的生产流程主要为精炼、精轧、精整、质量自动检测、长尺化生产等。与传统的模铸加工普通孔型法轧制工艺相比，现代的生产工艺不仅可以保证钢轨的几何尺寸更加精确，而且可以使钢轨具有良好的内在质量和表面质量[19]。本文不考虑生产工艺导致的不利因素，以U71Mn钢轨为研究对象，参考既有的规范和文献[20-23]，选定的离散元模型细观力学参数如表1所示。

表1 离散元模型的细观力学参数Table 1 Micromechanical parameters of the discrete element model

1.2 模型参数的验证

为了保证离散元法建立的钢轨模型具有可靠性，对钢轨抗拉强度进行试验仿真。根据相关标准[24]，对宽度d为10 mm、长度为50 mm的钢材试样进行拉伸试验和离散元仿真，拉伸前后的钢材试样如图1 所示，经轴向拉伸后得到的钢材应力-应变曲线如图2所示。

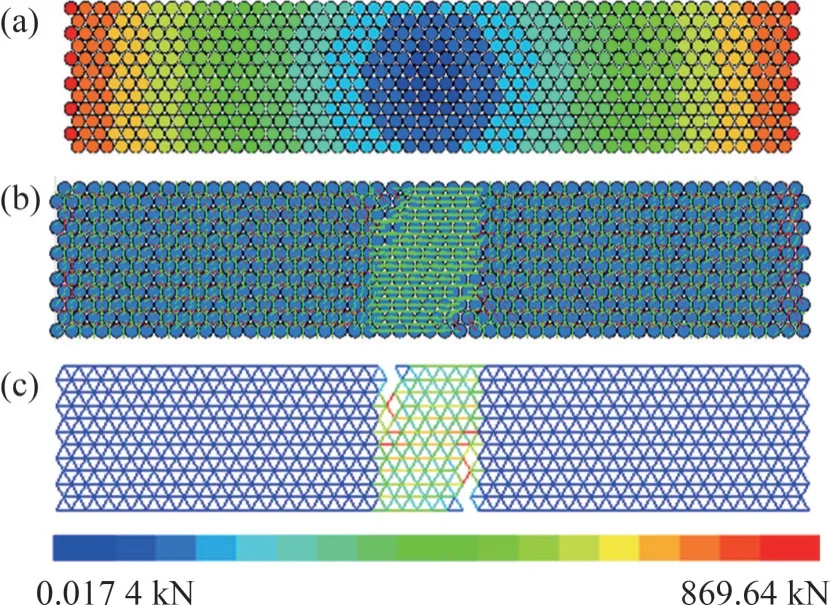
图1 拉伸前后的钢材试样Fig. 1 Steel samples before and after stretching

图2 钢材试样的应力-应变曲线Fig. 2 Stress-strain curves of steel sample

从图1可以看出：拉伸前钢材内部接触力分布均匀，钢材各向同性；钢材拉伸后，在中间部位的受力最大，并且在该处出现了部分接触力链的断裂情况。图1(b)中，蓝色球体颗粒表示构成钢轨的微观颗粒，绿色短线代表拉力，红色短线代表压力。从图1(b)可以看出：在钢材中间一定区域内，钢材试样主要受到拉力的作用，而在其他区域受到拉力和压力的共同作用；随着轴向拉伸不断进行，试样的中间部位由于所受拉力过大而出现接触力链断裂的情况，此时，钢材试样达到屈服状态。

工程上规定[25]，将试样产生0.2%塑性变形时对应的应力作为该材料的屈服强度。由图2 可知：钢材试样应变为0.2%时的拉应力为810 MPa，与本文选定的屈服强度非常相近，并且根据文献[26]的应力-应变曲线可以验证本文选取的离散元力学参数是可信的，可以在此基础上继续进行模拟研究。

1.3 钢轨的初始模型

为了探究钢轨在不同工况下的服役性能及其损伤特性，分别对钢轨横截面和钢轨接头纵断面进行2D离散元仿真。采用的主要建模方法是：将钢轨模拟为由ball组成的颗粒簇，并设定各个球体颗粒之间的接触属性；对于车轮的模拟方法，在分析静力作用时，为了便于加载，用clump单元模拟钢轨横截面上的车轮，用ball单元模拟钢轨纵断面上的车轮。在研究钢轨伤损时，为加快程序运行速率，用wall 单元模拟车轮。本文以钢轨为主要研究对象，而不考虑车轮的变形，在钢轨横纵断面均将车轮视为刚体。

钢轨横截面与接头纵断面的仿真初始模型如图3 所示。其中，车轮选用LM 磨耗型车轮踏面，据文献[27]，磨耗型车轮踏面对应的轮轨接触应力限值为1 600 MPa。

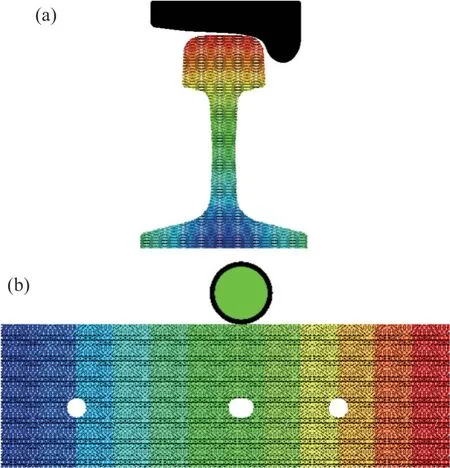
图3 钢轨初始模型Fig. 3 The initial models of rail

通过对车轮施加荷载以实现对钢轨间接加载。由于施加的荷载是轮轨接触力，其中包含了车轮重力，所以，模拟时车轮的直径对加载力没有影响。为使图形显示更加直观，图3(a)中的车轮仅展示部分区域，图3(b)中的车轮直径缩小为原来的1/10。

2 钢轨横断面的受力特性

2.1 静力分析

为了避免由于突然施加较大荷载而产生的冲击作用，对钢轨进行分级静力加载，分级加载的次数为100 次，直至达到目标荷载为止。据文献[28-29]，并取轮轨最易受损的加载条件，最终选用的轮轨横向作用力为10 kN，垂向作用力为150 kN。钢轨横截面接触力分级静力加载曲线如图4所示。

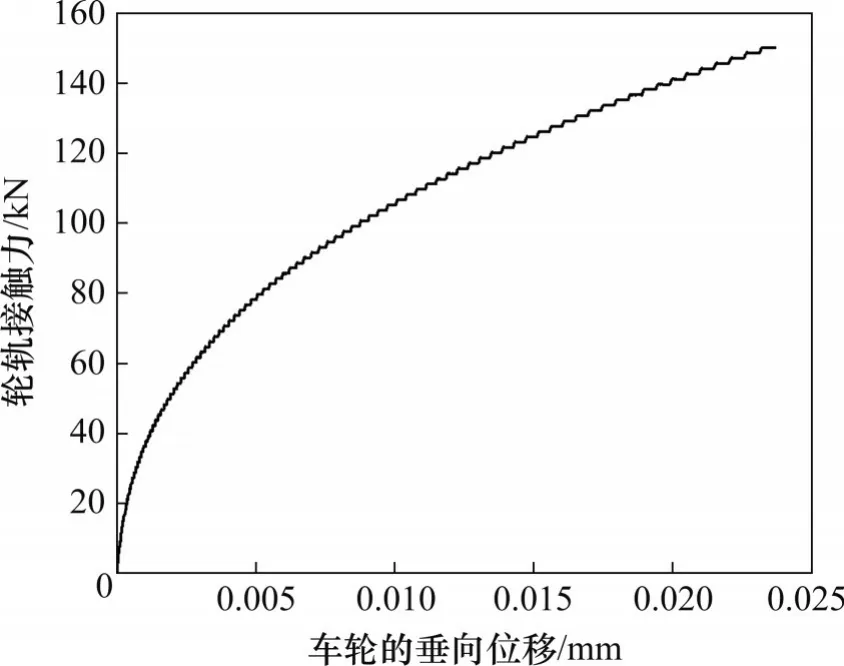
图4 钢轨横截面接触力分级静力加载曲线Fig. 4 Grading static loading curve of contact force of cross-section rail

静力加载后钢轨横截面的接触力分布情况如图5所示。

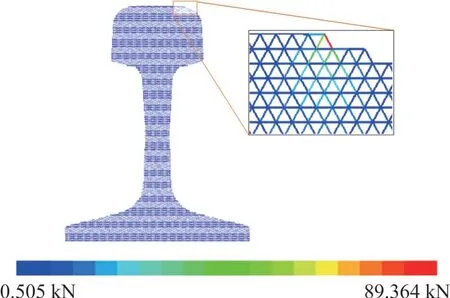
图5 静力加载后钢轨横截面接触力分布Fig. 5 Contact force distribution of rail cross section with static loading

由图5可知：在静力荷载作用下，轮轨接触力主要由轮轨作用点附近的颗粒承担，离接触点较远的钢轨内部颗粒受静载力作用较小。

2.2 钢轨伤损

随着列车的往复运行，轮轨间的接触面由于受车轮踏面缺陷、钢轨表面不平顺、轮轨之间的冲击、道床沉降等不利因素的影响，钢轨顶面的平顺性逐渐下降。对车轮施加竖直向下的位移作用，直至垂向位移达到10 mm，以便于分析钢轨在车轮不同垂向位移下的伤损及裂纹分布，从而间接反映轨道不平顺对轮轨接触力的影响。横截面钢轨的伤损演变情况如图6所示。建立轮轨离散元初始模型时，为了避免初始的轮轨接触力对后续车轮移动产生的轮轨接触力的影响，设置轮轨在初始阶段并没有绝对接触(即初始轮轨接触力为0 kN)，即车轮与钢轨轨头之间有较小间隙；后续随车轮竖向移动，轮轨间才逐渐产生接触。

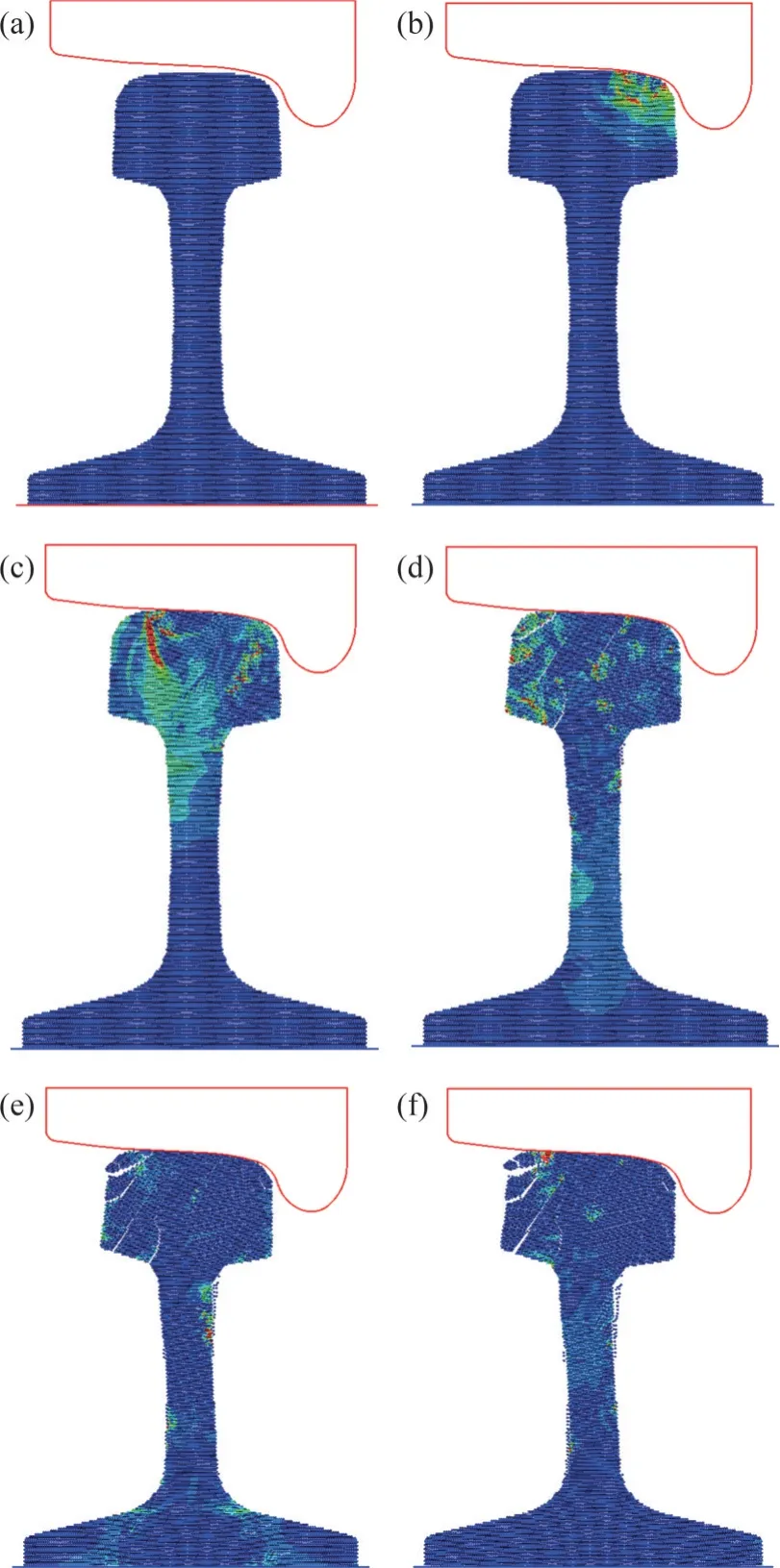
图6 横截面钢轨-伤损演变情况Fig. 6 Cross section rail-damage evolutions

从图6可以发现：随着车轮垂向位移增大，钢轨的伤损程度逐渐加大，在车轮垂向位移为2 mm时，主要在轮轨接触作用点附近产生较大的应力，几乎没有裂纹产生；当车轮垂向位移为4 mm 时，钢轨轨头产生较小程度的倾斜，可增大轮轨接触面，减少接触应力；当垂向位移为6 mm时，轨头处产生明显的裂纹；当垂向位移为8 mm时，轨头上颚的裂纹即将贯穿至钢轨顶面，并且在轨腰位置出现部分伤损现象；当车轮垂向位移为10 mm时，轨头的裂纹数量没有明显增多，但裂纹宽度逐渐增大，并在轨头和轨腰出现掉块现象，钢轨基本丧失其承载能力。

轮轨之间接触力随车轮垂向位移的变化趋势如图7所示，据图7可对钢轨伤损的力学性能进行定量分析。

图7 钢轨伤损的力学性能Fig. 7 Mechanical performance of rail damage

从图7 可见：由于在初始时轮轨之间没有接触，随着车轮的竖向移动逐渐产生接触力，所以，当车轮垂向位移小于1 mm时，轮轨间的接触力较小；当车轮垂向位移超过1 mm时，轮轨接触力随着车轮垂向位移增大而显著变大；当位移增大到4 mm时，轮轨接触力达到最大，而后随着垂向位移增大，轮轨接触力逐渐减小；当位移达到8 mm时，轮轨接触力又出现了小幅度提高。这是因为当垂向位移达到4 mm后，钢轨轨头出现了细小裂纹，并且裂纹数量随着位移增大而增多，从而导致其承载力有所下降；当位移达到8 mm时，钢轨出现了较明显塑性变形，钢轨与车轮的接触面积增大，其后的轮轨接触力也有所增加。

3 钢轨接头纵断面的受力特性

3.1 静力分析

钢轨接头是轨道结构的薄弱环节，故选取接头处一定长度范围内的钢轨进行研究。建立离散元钢轨纵向模型时，考虑到钢轨的轨头、轨腰、轨底3部分的横截面面积不相等，若直接采用钢轨的密度进行属性赋值则存在较大的偏差，因此，对钢轨密度赋值时，将轨头、轨腰、轨底3部分的颗粒密度按照相应部位的面积比例进行分配。钢轨纵向长度的选取以包含实际接头孔洞为原则，最终选取长度为600 mm的钢轨作为研究对象。为了用离散元法分析钢轨在压力作用下的力学性能，本文在纵向钢轨试样底部添加1个与其等长的wall单元，仅考虑钢轨在轮载作用下的压应力分布。

对于钢轨纵断面，分别取接头最左端、第1个螺栓孔、第2 个螺栓孔、第3 个螺栓孔、最右端5个位置添加车轮，以便于探究不同位置的车轮对钢轨受力性能的影响。车轮在纵断面钢轨的分布如图8所示。

图8 车轮在纵断面钢轨的分布Fig. 8 Distribution of wheels in the longitudinal sectionof rail

对钢轨纵断面进行静力加载时，采取与钢轨横截面静力加载类似的方式，均采用分级加载。静力加载后，车轮在不同纵向位置时的轮轨接触力见表2。

表2 车轮在不同位置时的轮轨接触力Table 2 Wheel-rail contact force when the wheels are in different positions

分析表2可以发现：当车轮位于钢轨孔洞位置上方时，Wheel_2、Wheel_3、Wheel_4 三者的轮轨接触力相差不大；而当车轮位于研究对象的两端时，轮轨接触力较大，约为孔洞位置轮轨作用力的2倍。出现该结果的原因是，位于钢轨试样两端的车轮由于其一边没有钢轨处于悬空状态，仅由车轮另一边钢轨承担传递的荷载，从而产生了较大的接触力。

由上述研究可知，接头处容易出现钢轨低头压溃等病害，其原因是：一方面，钢轨接头的螺栓孔减小了钢轨的截面，其承载力降低，同时，在孔洞处易产生应力集中现象；另一方面，钢轨接头存在轨缝，当列车运行到轨缝时，该处的钢轨由于部分悬空而将荷载不均匀地传递至轨缝两侧的钢轨，从而导致两侧钢轨由于受力不同而出现不同程度的沉降，使得轨道结构的平顺性及其服役性能进一步降低。

3.2 钢轨接头伤损

当车轮的垂向位移达到10 mm 时，不同工况下的钢轨内部颗粒接触力云图如图9所示。

图9 不同工况下的钢轨内部颗粒接触力云图Fig. 9 Contact force cloud diagrams of balls inside the rail under different working conditions

图9(a)所示为车轮位于Wheel_3时钢轨内部颗粒间的接触力分布云图，可见在轮轨作用点附近的接触力较大，距离作用点较远处的接触力均较小。当车轮作用在不同位置时，作用点附近的接触力分布情况见图9(b)。从图9(b)可见：当车轮位于3个螺栓孔上方时， Wheel_2、 Wheel_3、Wheel_4三者的钢轨颗粒接触力分布情况类似，并且沿车轮中心轴对称分布；而位于接头两端的车轮由于车轮荷载仅由一边的钢轨承担，导致其实际承载力与中间钢轨承载力相比较大，并且钢轨两端均是一边处于自由状态，钢轨内部颗粒在较大荷载且不受约束的状态下容易出现掉粒、剥落现象。

在车轮垂向下移时，分别对不同车轮位置的钢轨应力进行监测，得到钢轨轨头、轨腰、轨底的应力随车轮垂向位移的变化情况。由于车轮在不同位置时的应力变化情况相似，因此，只列出车轮位于Wheel_3时，钢轨不同部位的应力随车轮垂向位移的变化，如图10所示。

图10 Wheel_3-钢轨不同部位的应力随车轮垂向位移的变化曲线Fig. 10 Wheel_3-Curves of stress changes in different parts of the steel rail with vertical displacement of the wheel

由图10 可知：随着车轮垂直向下移动，轨头由于与车轮直接作用而产生较大的应力并且远大于轨腰和轨底的应力，轨腰部位的应力次之，轨底处的内部颗粒应力最小。

当车轮位于不同位置时，对应的钢轨应力变化如图11 所示，据图11 可分析车轮位置对钢轨不同部位的影响。

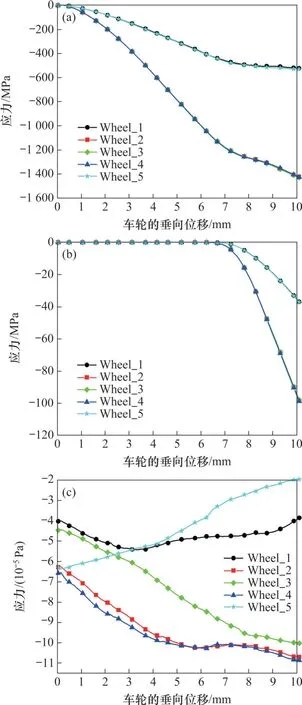
图11 钢轨不同部位的应力变化Fig. 11 Stress changes in different parts of the rail

由图11(a) 可知：当车轮位于Wheel_2、Wheel_3、Wheel_4 时，车轮位置对轨头应力随车轮垂向位移的变化几乎没有影响，3条曲线基本重合；当车轮位于Wheel_1、Wheel_5 时的轨头应力变化曲线也几乎重合，并且均小于Wheel_2、Wheel_3、Wheel_4 对应的轨头应力。轨腰应力曲线变化情况与轨头的应力曲线变化情况类似，但随着车轮垂向位移增大，轨头应力的增大速率逐渐减小，而轨腰应力的增大速率不断提高。这说明随着车轮向下移动，钢轨承受的荷载由以轨头承受为主转换为以轨腰承受荷载为主。

从图11 可见钢轨主要由轨头承受荷载，其次是轨腰，轨底对承载的贡献较小。虽然不同车轮位置的轨底应力不相同，但轨底应力均很小，并且相差不大。

4 结论

1) 轮轨接触力随车轮垂向位移增大，出现先增大后减小再增大的变化；接触力减小的原因是轨头产生细小裂纹，之后再增大的原因是钢轨发生了塑性变形。

2) 作用在钢轨轨缝的车轮由于其一边处于部分悬空状态，导致轨缝两侧的钢轨受力不均匀，容易产生钢轨低头、折角、台阶等现象。

3) 当车轮分别位于钢轨接头处的3个钢轨螺栓孔上方时，钢轨应力相差不大；当车轮位于钢轨端部时，应力曲线重合；不同车轮位置的钢轨应力均随着车轮垂向位移增大而增大。

4) 轮轨间接触力主要由钢轨轨头承担，轨腰分担的荷载次之，轨底分担的荷载最小。随着车轮向下移动，轨头承担的荷载逐渐向轨腰移动和传递。