基于低场核磁共振的二元结构含水层LNAPL迁移及分布规律研究

李胜，窦智，陈永强，马晓凡，王锦国，周志芳

(河海大学 地球科学与工程学院，江苏 南京，210000)

地下水遭受石油类非水相液体污染已成为全球性的水安全问题[1-2]。近年来，我国城市化、工业化发展迅速，石油类化工产品的需求量和使用量急剧增加，储存、运输的规模不断扩大。我国现有加油站10 万余座，使用中的地下储油罐有数十万个。据调查显示，苏南地区约72%的加油站的地下储油罐出现了不同程度的泄漏[3]，周边地区地下水环境受到不同程度的污染。石油类非水相液体侵入地下水后往往成为长期的地下水污染源，且此类污染物具有不溶于水、毒性强、难降解等特点，治理难度较大。轻质石油产品类污染物的密度普遍比水小，称为轻非水相液体(light nonaqueous phase liquid，LNAPL)，探究LNAPL 侵入地下后其迁移和分布规律对预防和治理此类污染物有着重要的意义。

LNAPL 侵入地下水后，其迁移和分布规律十分复杂，国内外学者对此开展了大量研究[4]。有研究认为，LNAPL 出现泄漏进入地下后，通常以垂向迁移的方式穿过包气带，到达地下含水层后发生横向扩散[5]。另有研究认为，LNAPL 到达含水层后，部分污染物会出现穿过含水层的现象，污染深度进一步增加[5-6]。整体而言，以往有关LNAPL迁移规律的研究主要针对正常层位地层(常规地层)[4-6]，此类地层中含水层的孔隙普遍比包气带地层的小。然而，在自然界中同样存在诸多因地壳运动引起层位变化的地层，诸如地层倒转(被压实的老地层覆盖在松散的新地层之上)的现象。若LNAPL 在此类地层中出现泄漏，则其迁移规律将更为复杂[7-8]。

目前，研究LNAPL 在倒转地层中迁移规律的成果较少。地层倒转后，毛细管力、重力的影响方向等因素会发生改变。另外，由于多孔介质孔隙结构本身具有随机特性，其内部流动是一个极为复杂的过程，使用一般的物理方法难以描述[9]，室内试验无疑是相对合理的研究手段。观测土样、砂样等多孔介质孔隙结构分布情况的试验方法主要有压汞法、吸附法以及核磁共振法[10]等。其中，核磁共振(NMR)是一种无损、快速的检测技术。近年来，诸多学者将NMR 应用到多孔介质领域。孙晓彤等[9]采用NMR 技术测得煤样吸水量和含水量的时间与空间演化规律。张倩等[10]结合核磁共振谱分析与成像技术，研究了自吸过程中水在人工砂岩中的迁移规律。本文基于低场核磁共振技术，采用材质均一、粒径不同的2种玻璃砂，分别与饱和水、柴油构建“上粗下细”型常规二元结构地层和“上细下粗”型倒转二元结构地层，结合T2分布曲线分析，从微观角度研究LNAPL的时间与空间演化过程，探讨倒转地层中LNAPL 的迁移规律。

1 试验材料与方案

1.1 核磁共振原理

含1H 原子的流体运动规律在多孔介质中具有独特的弛豫机制。在梯度磁场中，含水层中孔隙水的横向弛豫时间T2与自由弛豫时间T2B、表面弛豫时间T2S和分子扩散弛豫时间T2D有关。在环境温度稳定和试验磁场均匀的条件下，对于多孔介质中的孔隙水，T2B远大于T2S和T2D，因此，本试验可以忽略1/T2B对T2的影响；另外，孔隙水满足快速扩散条件，1/T2D对T2的影响也可以忽略。同时，假设多孔介质中的孔隙形态为球形，建立孔隙半径R与T2的转化关系式为

式中：T2为横向弛豫时间，ms；ρ2为横向弛豫率，μm·s-1。

由式(1)可以看出，多孔介质中孔隙水所处的空间半径与T2呈正相关，T2越大，对应的孔隙空间半径越大。

1.2 试验材料与设备

结合土力学[11]中的土颗粒分级，选用材质均一、粒径差异较大的2种玻璃砂制作二元结构，分别用于模拟粗砂层和极细砂层，其中，粗玻璃砂的粒径范围为0.400 0～0.600 0 mm，平均粒径为0.500 0 mm；细玻璃砂的粒径范围为0.071 0～0.090 0 mm，平均粒径为0.080 5 mm，玻璃砂均采购于广东兆通玻塑科技有限公司。LNAPL 污染物选用0 号国标柴油(采购于中国石油吉印路加油站)，此类柴油在日常生产生活中的使用范围较广，属于常见的轻非水相液体污染物。本试验使用的玻璃砂不具有亲油特性，与实际地层中土壤的亲水疏油性一致。另外，玻璃砂颗粒表面光滑，柴油在孔隙中运移时受到的摩阻力和黏滞力可以忽略。试验用水为烧开冷却后的去离子水，去离子水中含有的杂质少，烧开后冷却可有效去除水中原本存在的气泡，避免气泡和杂质对试验结果产生影响。0号柴油物理化学性质见表1。

表1 0号柴油物理化学性质Table 1 Physical and chemical properties of No.0 diesel

在NMR测试过程中，磁场始终保持稳定对试验结果的准确性极为重要。为避免铁磁性物质干扰磁场，采用定制的聚四氟乙烯空心圆柱状模具作为试样的样品管(直径×高为25 mm×55 mm)，聚四氟乙烯不含铁磁性物质且硬度高，抗腐蚀性能强，在试验过程中不与柴油发生化学反应，并且能够有效排除模具本身对磁场信号的干扰，同时，较高的硬度便于玻璃砂的压实、饱和等试验操作。试验使用的核磁共振测试设备为苏州纽迈公司研制的MacroMR12-150H-I 型大口径核磁共振分析仪，其永磁体温度为32.0 ℃，共振频率为13.05 MHz。本试验采用的NMR测试序列为CPMG序列，此脉冲序列可在1次测量中通过样品多组回波串进行探测，大大提高测量精度，缩短测量时间，是目前多孔介质领域观测孔隙时常用的NMR 测试序列。CPMG序列参数见表2。

表2 CPMG序列参数Table 2 CPMG sequence parameters

1.3 试验方法

试验设置4组单层饱和多孔介质试样S1～S4用于信号差异性分析，设置4组二元结构多孔介质试样D1～D4 进行常规地层和倒转地层流体运移规律分析，其中，D1和D2试样用于模拟常规二元结构地层，D3 和D4 试样用于模拟倒转二元结构地层，试样装填方式见表3。

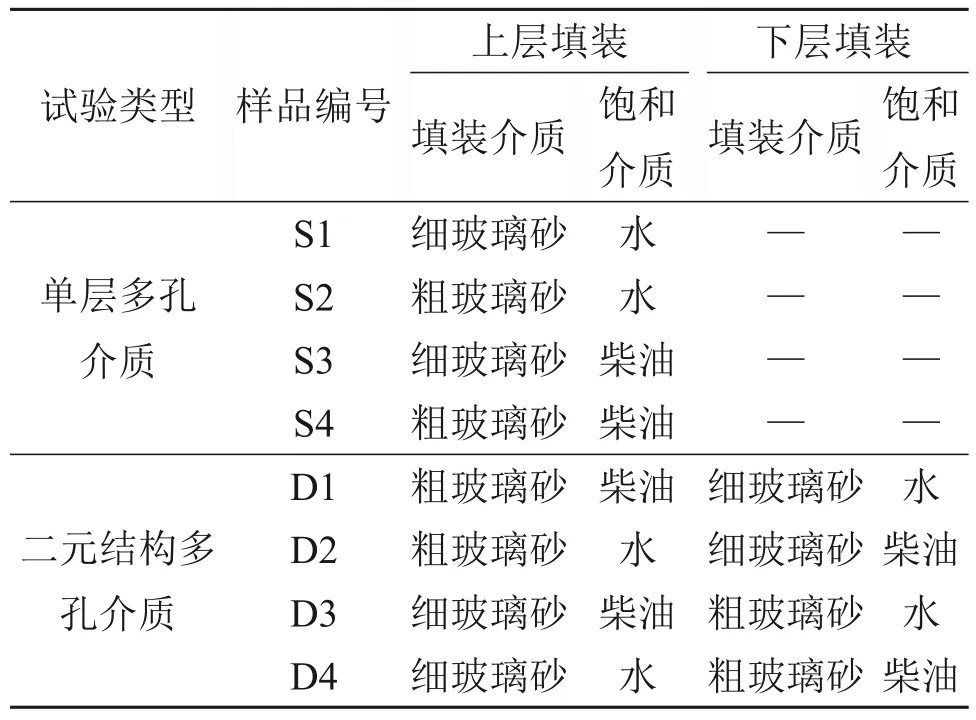
表3 试样装填方式Table 3 Sample filling mode

试样的制备和测试步骤如下：1) 准备饱和砂。取不同粒径玻璃砂加入去离子水浸泡，水面须高于玻璃砂表面1 cm 以保证完全浸没，并置于室温(25 ℃)下浸泡24 h。柴油的饱和方式同上，但由于柴油易挥发，加入柴油后，容器需进行保鲜膜密封以及遮光处理，浸泡时间缩短至3 h。2) 制备测试试样。饱和完成的砂样按照表3所示的装填方式装入试样模具，单层多孔介质的填装高度为55 mm，双层多孔介质的分层位置在模具底部27.5 mm处，填装时借助标示线与填装后模具对光时产生的阴影线可以判断准确填装位置。在填装过程中边填装边捣实，室内温度均为25 ℃。3) NMR测试。测试试样制备完成后，立即将试样置于核磁共振分析仪中进行测量，根据测试结果绘制T2分布曲线。测试完成后将试样置于25 ℃恒温箱。每隔1 h 取出试样重复NMR 测试，测量至样品T2曲线无明显变化即终止试验。

在正式试验前已进行多次预实验，以保证同种装填方式试样的T2曲线几乎相同，从而保证同种粒径玻璃砂组成的多孔介质内部孔隙结构几乎相同。

2 结果与讨论

2.1 水油信号差异分析

试样S1～S4 的T2曲线如图1 所示。从图1 可见：对于以相同粒径玻璃砂为介质的试样，水、油流体激发的信号明显不同，饱和柴油试样S3 和S4的峰值分别比饱和水试样S1和S2的峰值高；对于以不同粒径玻璃砂为介质的柴油试样S3 和S4，测试信号激发时间集中出现在100～1 000 ms，从而无法区分试样孔隙大小。由于柴油与水的分子含氢量有很大不同，分子扩散弛豫时间和自由弛豫时间也存在差异，因此，饱和柴油试样不满足T2与孔隙空间的对应关系(式(1))。根据饱和水试样T2测试结果，采用式(2)可计算砂样孔隙空间的T2信号强度平均值，代入式(1)可计算其平均孔隙半径。经计算可得：S1和S2试样的平均孔径分别为23.92 μm 和4.06 μm，S3和S4试样的平均孔径分别为1.46 μm和1.02 μm。可见，在相同的孔隙下，柴油信号的计算结果远远偏离实际情况，无法准确地判断流体的空间分布以及迁移规律。

图1 S1～S4试样的T2分布曲线Fig. 1 T2 distribution curve of sample S1-S4

式中：T2i为各测试时间节点；Ai为各测试节点激发的信号强度；A为所有信号的累加强度。

2.2 常规地层中LNAPL运移规律

常规地层污染物的泄漏一般为顶部泄漏和内部泄漏[12]。图2 所示为D1 和D2 试样的NMR 信号强度随横向弛豫时间的变化。

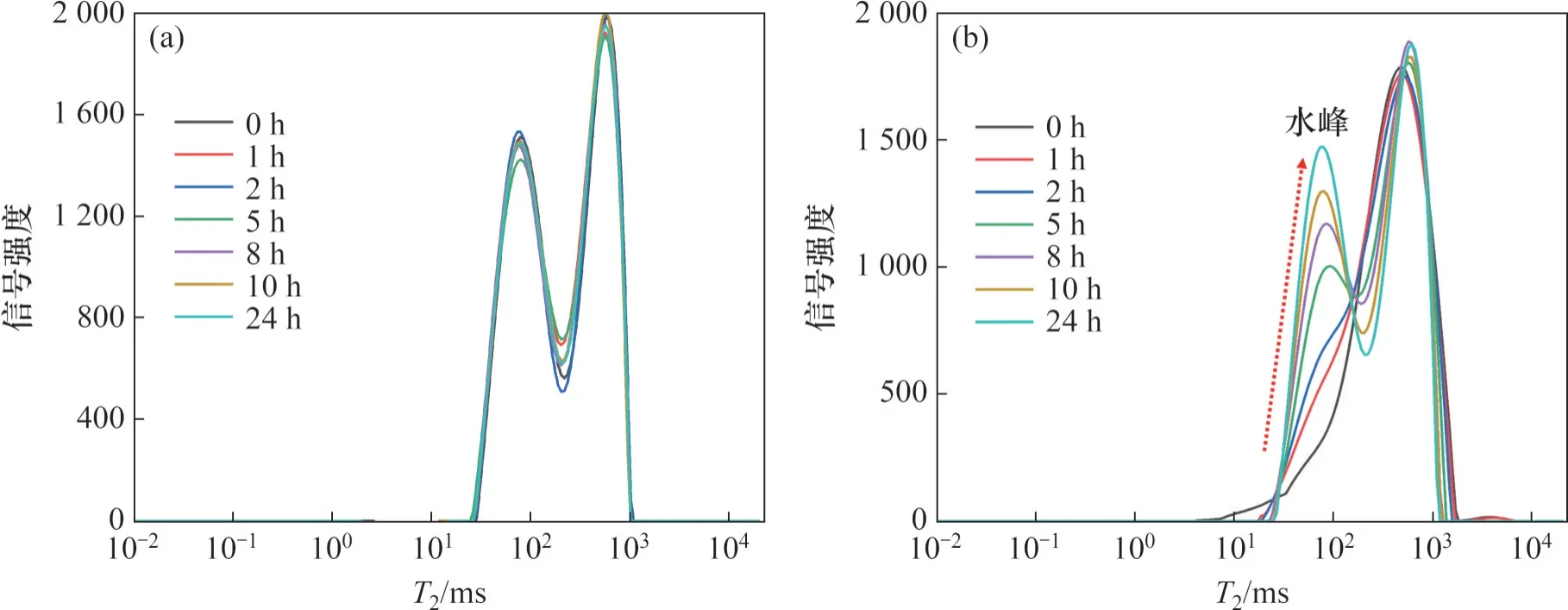
图2 D1和D2试样的T2谱线Fig. 2 T2 spectrums of sample D1 and D2

采用D1 试样模拟污染物在含水层顶部泄漏的情况，常规地层顶部受到大量LNAPL 污染时，污染物在粗砂层中快速入渗到达含水层顶部，此时，局部粗砂层处于饱油状态。从图2 可见，D1 试样的NMR测试信号初始即存在2个明显的峰值(双峰曲线)；左侧峰值出现在80 ms 附近，右侧峰值出现在900 ms附近。对比单孔介质T2曲线(图1)可知左峰为水在极细砂层激发的信号，右峰为柴油在粗砂层激发的信号。粗砂层中LNAPL 与极细砂层含水层接触后24 h，样品T2曲线的双峰形态几乎不变，峰值有一定的波动，峰谷整体呈下降趋势，可以判断该体系内部出现水油分离的现象，但整体上并未发生水油流体的跨层迁移。

采用D2 试样模拟污染物在地下埋深较深处出现泄漏的情况。LNAPL 大量渗透进入下层极细砂层，使得极细砂层处于暂时饱油状态，地下水被“挤”到上层粗砂层。从图2可见，D2试样T2分布曲线在LNAPL 泄漏初期呈单峰形态，随着污染物的迁移扩散，单峰曲线逐渐向双峰曲线过渡(红色虚线指示过渡趋势)，新峰峰值的出现时间在80 ms附近，初始峰的位置略有向右移动的趋势，最终稳定在900 ms附近。对比图1可判断出新增的峰为水在粗砂层中激发的信号，900 ms 附近为柴油在细砂层中激发的信号。由此可知，D2 试样内部出现逆向渗吸的现象，粗砂层中的水大量迁移至极细砂层，极细砂层中的柴油进入到粗砂层，整体上呈现出LNAPL向上运移、水向下运移的趋势。

2.3 倒转地层中LNAPL迁移规律

D3和D4试样在污染物泄漏后24 h的T2分布曲线变化如图3所示。与常规地层一样，倒转地层污染物也存在2种泄漏方式。采用D3试样和D4试样分别模拟LNAPL 从顶部渗漏和内部渗漏的污染物迁移情况。

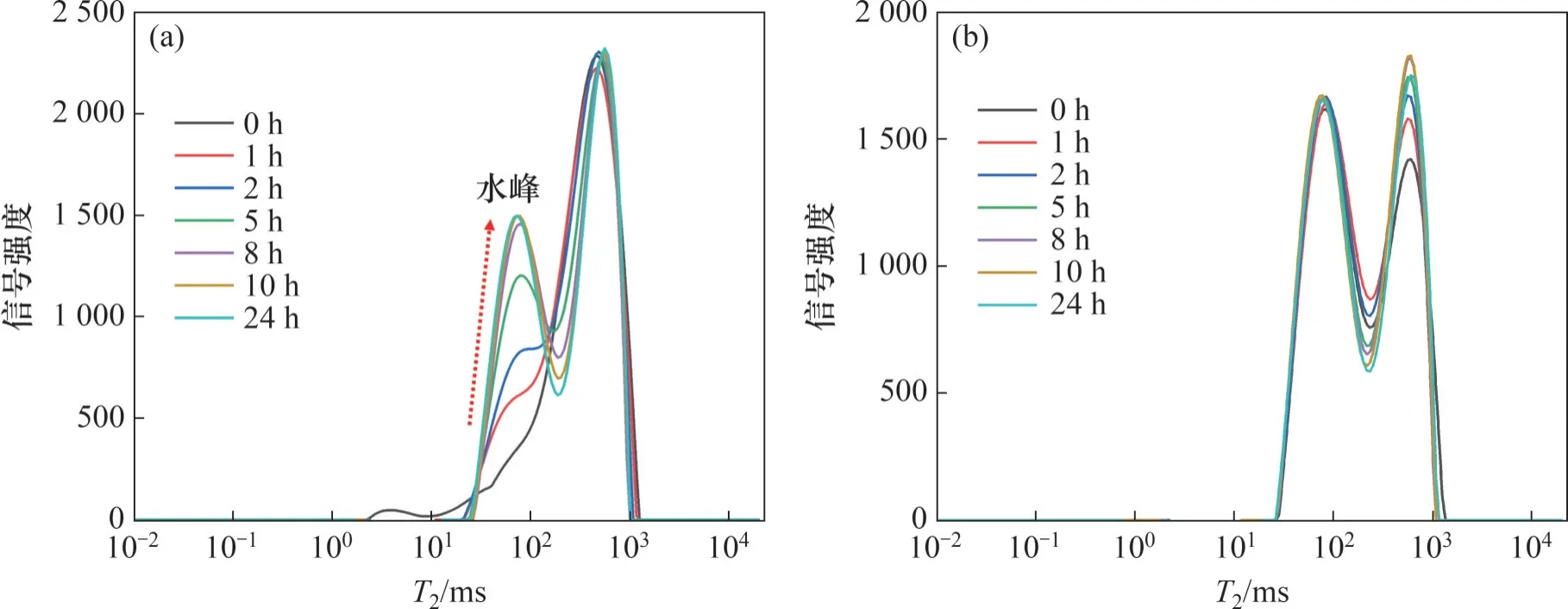
图3 D3和D4号试样T2谱线Fig. 3 T2 spectrums of D3 and D4 samples

从图3 可见，D3 试样的T2分布曲线总体形态与D2试样的相似，均由初始单峰曲线逐渐向双峰曲线过渡；D3 试样最终曲线的双峰峰值分别出现在80 ms处和900 ms处，分别为水在极细砂层和柴油在粗砂层中激发测得的信号。上述现象表明，当倒转地层顶部出现LNAPL 泄漏时，污染物的运移方式与常规地层中内部LNAPL 泄漏时的运移方式一致，均出现逆向渗吸现象。D4 试样的测试结果与D1 试样的测试结果基本一致，T2曲线均呈双峰形态。结果表明，出现内部LNAPL 泄漏的倒转地层中污染物迁移方式与常规地层顶部出现LNAPL 泄漏时的运移方式一致，均为水油分离后处于稳定状态。D4 试样的左侧峰值几乎不变，右侧峰值先升高后降低，峰谷整体呈现下降趋势。

2.4 二元结构中LNAPL的运移机理

NMR 的测试结果直观地反映了二元结构地层中LNAPL 的迁移规律。在二元结构地层中，LNAPL 的泄漏位置决定其迁移扩散的方式。当LNAPL泄漏在常规地层顶部或倒转地层内部时(D1和D4试样)，地层中的流体交换现象并不明显，污染物的迁移主要以横向扩散为主，LNAPL 几乎不会进入含水层中；然而，当LNAPL 泄漏在常规地层内部或倒转地层顶部时(D2 和D3 试样)，污染物会以逆向渗吸的方式与含水层发生流体交换，以此造成更为严重的地下水污染。

横向扩散的污染物的运移方式大多遵循对流弥散方程[12]，而自发渗吸的过程受多种因素的影响。基于自吸的基本静力学与动力学，渗吸过程多与毛细管力、黏滞力、惯性力和重力有关[13]。本试验不考虑惯性力的影响，且黏滞力始终存在于发生运移的流体内部，与空间位置无关，因此，二元结构中逆向渗吸过程以及渗吸效率主要受毛细管力和重力的影响。为研究二元结构地层中，不同流体的毛细管力以及流体重力对逆向渗吸过程的影响，引入逆Bond数、毛细管力PC以及预测模型进行定量分析，结合试验数据，分析常规地层内部以及倒转地层顶部出现污染物泄漏时的渗吸过程。

采用逆Bond 数NB研究重力的影响。逆Bond数的计算公式[14]为

式中：C1为常数，在毛细管模型中，通常取0.4；σ为界面张力，mN/m；Δρ为介质密度差，g/cm3；H为试样长度，cm；φ为孔隙度；k为渗透率，m2。

逆Bond数NB可以用于判断多孔介质内部流体发生迁移时所受到的主要驱动力类型。当时，多孔介质自吸过程中毛细管力起支配作用；当时，重力作用才作为主要驱动力；当1＜NB≤5时，毛细管力和重力共同作用于自吸过程。

在NMR 测试试验中，孔隙半径R可以通过横向弛豫时间计算。选择材质相同、分选良好的玻璃砂作为多孔介质的组成材料，可以通过控制玻璃砂的粒径得到不同渗透率的多孔介质模型。用玻璃砂进行试验时，绝对渗透率k通常用Kozeny-Carman[15]方程表示：

式中：KZ为科泽尼常数，对于分选良好的砂粒或球形填充材料，KZ≈5。

玻璃砂填装试样的比表面积S可用S=3/R计算。经测定，细玻璃砂和粗玻璃砂填充而成的介质孔隙度分别为0.373 6和0.316 9，故结合式(3)和式(4)可建立逆Bond数与颗粒半径、孔隙度、样品长度的关系为

式中：r为颗粒半径；c为常数。

经计算，在粗砂层和极细砂层中，水的逆Bond 数分别为5.085 1 和26.003 6，柴油的逆Bond数分别为1.470×10-4和9.262×10-4。结果表明，在二元结构自发渗吸过程中，水的迁移主要受毛细管力驱动，重力作用可以忽略不计；柴油的迁移主要受重力影响，毛细管力的作用影响较小，可以忽略。

多孔介质中，毛细管力Pc可以使用Laplace-Young(L-P)方程计算：

式中：θ为流体与玻璃砂之间的接触角。

根据式(6)计算不同地层水油流体的毛细管力，计算结果见表4。

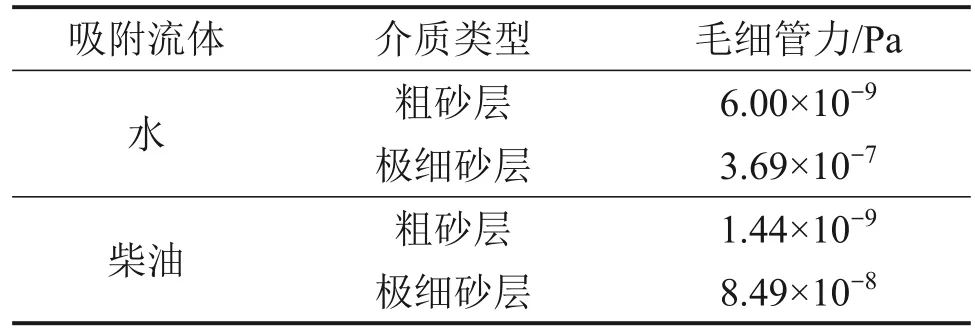
表4 毛细管力计算结果Table 4 Calculation results of capillary force

从表4可见：极细砂层对水的毛细管力远超各地层对柴油的毛细管力；粗砂层对水、油流体的毛细管力较接近，且与极细砂层对水的毛细管力相差2个数量级，说明二元结构中逆向渗吸过程的主要驱动力为极细砂层对水的毛细管力以及柴油自身重力的共同作用力，这与逆Bond 数所得结论相符。结合图3和图4中水的运移过程，极细砂层对水的毛细管力为主要驱动力，其牵引方向决定了逆向渗吸过程中水的渗吸方向；而LNAPL 重力不会影响渗吸方向，仅仅改变逆向渗吸的完成效率。

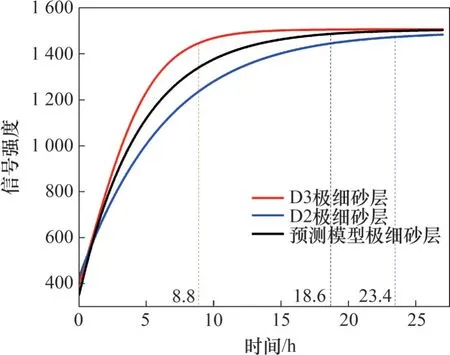
图4 预测模型与D2、D3试样极细砂层信号强度对比Fig. 4 Comparison of signal strength of prediction model and ultra-fine sand layer of D2 and D3 samples

为研究重力作用对LNAPL 迁移效率的影响，引入WASHBURN[16]提出的岩石吸水动力特征的理论模型进行模拟预测。该模型可以预测在无重力作用下，多孔介质内流体渗吸高度随时间的变化情况。对本试验的试样模型进行简化处理，假设二元结构内部的毛细管平行且直径相同，不考虑重力影响时，液体吸入的速率取决于毛细管力，吸入高度h随时间t的变化可表示为[16]

式中：η为水的黏度。

此模型可预测不考虑重力的情况下二元结构含水层发生渗吸时水的上升高度，将预测结果与D2和D3试验的观测结果进行比较即可评估重力对LNAPL 运移效率的影响程度。将计算结果代入ExpDec3单指数拟合模型[17]中，可将上升高度转化为NMR信号强度，模型公式如下：

在不同情况下，极细砂层含水量的变化如图4所示。从图4可见：在二元结构地层中，对于常规地层、倒转地层以及预测模型地层，极细砂层中水的NMR信号强度初始值和最终值极为接近，信号强度均从自410 左右增加至1 480 左右后呈水平形态分布，增加速率均随时间减缓。此现象说明，D2和D3试样内部发生了同样的渗吸过程，渗吸水量也几乎相同，且均符合岩石吸水动力特征理论模型。该结果也验证了水的重力对自发渗吸过程的影响甚微的结论。

然而，由于LNAPL重力的影响，D3试样的渗吸效率远高于D2 试样的渗吸效率，D2 试样和D3试样完成渗吸过程所用时间分别为23.4 h 和8.8 h。在二元结构自发渗吸过程中，D3 试样柴油的渗吸方向与重力方向相同；D2 试样柴油渗吸的方向则与重力方向相反。通过控制地层空间位置，从而引起渗吸方向与重力方向发生变化，可使渗吸效率发生改变。当逆向渗吸方向与LNAPL 重力方向相同时，渗吸过程加快，相比于预测模型，渗吸效率提高52.69%；当重力方向与LNAPL渗吸方向相反时，则减缓渗吸过程的进行，渗吸效率减少25.80%左右。

3 结论

1) 有机污染物和水的扩散系数存在明显差异，梯度磁场中其弛豫机制更为复杂，故在NMR测试中，有机污染物的T2信号出现集中现象，无法准确区分不同大小的孔隙空间，有机污染物的T2信号与孔隙空间的转换关系有待进一步研究。

2) 在二元结构地层中，LNAPL 的泄漏位置决定其迁移扩散的方式。当LNAPL 泄漏在常规地层顶部或倒转地层内部时，污染物的迁移主要以横向扩散为主，LNAPL 几乎不会进入含水层中；当LNAPL 泄漏在常规地层内部或倒转地层顶部时，污染物会以逆向渗吸的方式与含水层发生流体交换，造成更严重的地下水污染。

3) 在逆向渗吸过程中，毛细管力对水的牵引决定渗吸方向，LNAPL重力的存在影响渗吸速率。当渗吸方向与LNAPL 重力方向一致时，渗吸速率提高52.69%；反之，渗吸速率减少25.80%。