单一粗颗粒影响下的矿岩颗粒体系三维力链演化特征

孙浩，陈帅军，金爱兵，唐坤林，刘美辰，韦立昌

(1. 北京科技大学 金属矿山高效开采与安全教育部重点实验室，北京，100083；2. 北京科技大学 土木与资源工程学院，北京，100083)

地下矿山开采过程中，爆破作用或自然崩落形成的矿岩散体是一种复杂的颗粒物质体系，不仅具有无序性、多尺度性、能量耗散性、自组织行为以及非线性响应等典型颗粒物质体系的本质属性[1-3]，而且因矿岩颗粒粒径与形状的显著差异性[4]以及可破裂特性[5]等而形成独特的摩擦响应与流变关系等宏观统计规律。其中，矿岩颗粒体系中存在的不同粒径和位置的粗颗粒为主要影响因素之一。此外，重力作用下矿岩颗粒间相互碰撞、挤压形成的若干承载和传递力的链状结构即力链[6]，是连接细观尺度矿岩颗粒单体和宏观尺度矿岩颗粒体系的桥梁[7-9]，并直接影响放出体形态演化规律、矿石贫损指标等放矿过程与结果。因此，为了探明不同粗颗粒对矿岩颗粒体系运移与力学特性的影响机制，研究单一粗颗粒影响下的矿岩颗粒体系三维力链演化特征十分必要。

近年来，国内外学者通过室内试验和数值模拟等手段对不同颗粒物质体系力链演化特征开展了一系列研究。在室内试验研究中，光弹性测量技术(photoelasticimetry)能够实现定量且非接触测量颗粒体系内的受力状态和力链结构特征，因而被广泛应用于颗粒力学试验领域[10-11]。WANG等[12-13]基于光弹性测量技术探究了二维摩擦颗粒剪切阻塞相变的临界体积分数及其微观成因。WANG 等[14-15]通过二维光弹试验发现颗粒体系剪切局域化区域与沿最大剪切应力方向的两个极化应力场之间存在较强相关性，并揭示了局部各向异性在颗粒材料统计框架中的作用。王金安等[16-19]研发能够使颗粒实现双轴加载和双向流动的颗粒光弹试验装置，并提出混合颗粒体光弹力链定量提取方法，探究了断层破碎剪切带和放顶煤开采过程中力链结构、空间分布及其强度等特征。此外，陈凡秀等[20]基于数字图像相关方法(digital image correlation，DIC)[21]和牛顿力学定律获取颗粒接触的大小和方向，研究了动载颗粒体系力链破坏机制。在数值模拟研究中，IMSEEH等[22]开展渥太华砂的一维压缩有限元数值模拟，捕捉了颗粒体系力链的演化过程，发现力链主要在模型上下加载端之间传递荷载，同时四周颗粒为力链的屈曲提供有效支撑。HOU等[23]建立平板剪切模型，模拟无限平板条件下的颗粒剪切运动，利用力链的载荷分布率曲线和模式分别描述了力链的承载行为和形态变化，并定义了对角网格型、蝌蚪型和羽状等力链形式。而在放矿领域，韩连生等[24-26]基于离散元软件PFC 分别研究了端部放矿条件以及柔性隔离层下矿岩散体力链演化特征，为丰富放矿理论与技术提供了新思路。

目前，已有放矿理论与试验研究中并未充分考虑粗颗粒对矿岩颗粒流动特性的影响，从而导致所得研究成果与实际崩落法矿山放矿结果之间存在不小偏差。此外，放矿研究多集中于矿岩颗粒宏观运移特性，对于其细观力学研究尚浅；且已有矿岩颗粒体系力链研究存在定性分析多、定量表征少、系统性差等缺点，对其颗粒间动力学行为有待深入研究。因此，本文作者基于滚动阻抗模型(rolling resistance model)开展放矿数值试验，对单一粗颗粒影响下的松动体形态演化规律和矿岩颗粒体系三维力链宏观分布、数量、平均强度、准直性、长度与方向等演化特征进行量化研究。

1 放矿方案设计与三维力链识别

与基于颗粒离散元法的其他工程应用[27]一致，计算精度和计算效率亦是放矿颗粒流模拟中的一对矛盾体，而球形颗粒因其更高效的接触检测算法(contact detection algorithm)而在计算量和计算效率等方面具有突出优势。因此，本文基于球形颗粒和滚动阻抗模型[28]开展一系列单口底部放矿数值试验，研究不同粒径和位置单一粗颗粒影响下的矿岩颗粒体系三维力链演化特征。

1.1 放矿方案设计

本文作者前期已利用自制三维放矿室内试验模型(图1(a))开展若干放矿室内试验，并基于滚动阻抗模型(图1(b))开展放矿数值试验。通过对比分析放矿室内试验与数值试验结果，证明了滚动阻抗模型在放矿数值研究中的可靠性与优越性，并确定了如表1 所示球体和墙体相应的细观力学参数[29]，这为本次单一粗颗粒影响下的矿岩颗粒体系三维力链演化特征研究奠定了模型与参数基础。

图1 三维放矿室内试验模型与滚动阻抗模型示意图Fig. 1 3D physical draw model and sketch of rolling resistance model

表1 墙体与球体的细观力学参数[29]Table 1 Mesoscopic mechanical parameters of walls and balls[29]

图2(a)所示为本次模拟所用的单口底部放矿数值模型，模型底部红色区域为放矿口。图2(b)中绿色颗粒为本次模拟所用粗颗粒，其余颗粒均为细颗粒。为了更加突显模型中细颗粒空间高度与作用的差异性，将不同高度细颗粒设置成如图2(b)所示的三种不同颜色。

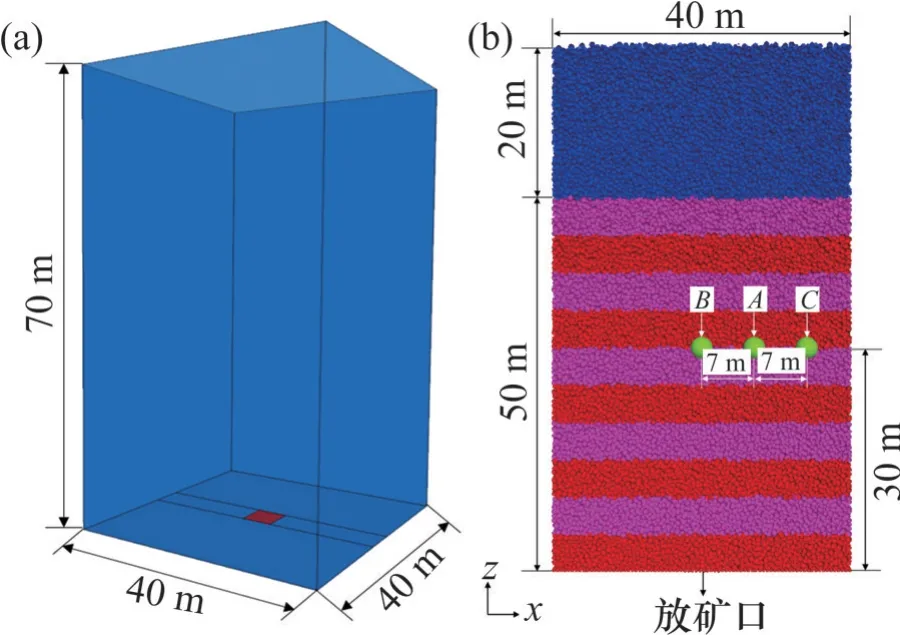
图2 放矿数值模型Fig. 2 Numerical draw model

放矿数值试验方案如表2所示，本次数值试验所用细颗粒粒径df范围为0.3～0.8 m，粗细颗粒粒径比dc/df范围为1.0～8.0。每组试验中的单一粗颗粒分别布设于放矿口正上方30 m 高度的A、B、C三个不同水平位置处(图2(b))。本次放矿数值试验方案可分为如下两类：首先，通过试验1～8明确能够对崩落矿岩流动特性产生显著影响的粗细颗粒粒径比dc/df；在此基础上，通过试验7、9 和10 对比分析不同空间位置粗颗粒对矿岩颗粒体系三维力链演化特征的影响。

表2 放矿数值试验方案Table 2 Schemes of numerical draw simulation

每组放矿数值试验过程如下：1) 基于滚动阻抗接触模型(图1(b))和“雨落法”[29]生成如图2(b)所示的放矿数值模型，赋予墙体与球体相应的细观力学参数(表1)，并统计初始平衡状态下粗颗粒四周局域内力链的数量、平均强度、准直性、长度和方向等特征参量；2) 打开放矿口开始出矿，监测、记录不同高度的松动体形态以及不同放矿阶段粗颗粒四周局域内的力链演化过程；3) 当矿岩颗粒放出高度达50 m 时，停止出矿，并在模拟过程中保持模型顶部20 m的覆岩高度不变。

1.2 三维力链识别

颗粒体系内由接触颗粒形成的可承载和传递力的链状结构即为力链[2]。力链识别判据及其示意图如图3 所示。颗粒间成链需满足如下三个条件[24-26]：1) 接触力判据，即颗粒间接触力不小于颗粒体系内的平均接触力；2) 接触角判据，即两相邻接触的方向向量间夹角不大于角度阈值θc；3) 成链颗粒数目不小于3，即成链接触数不小于2。

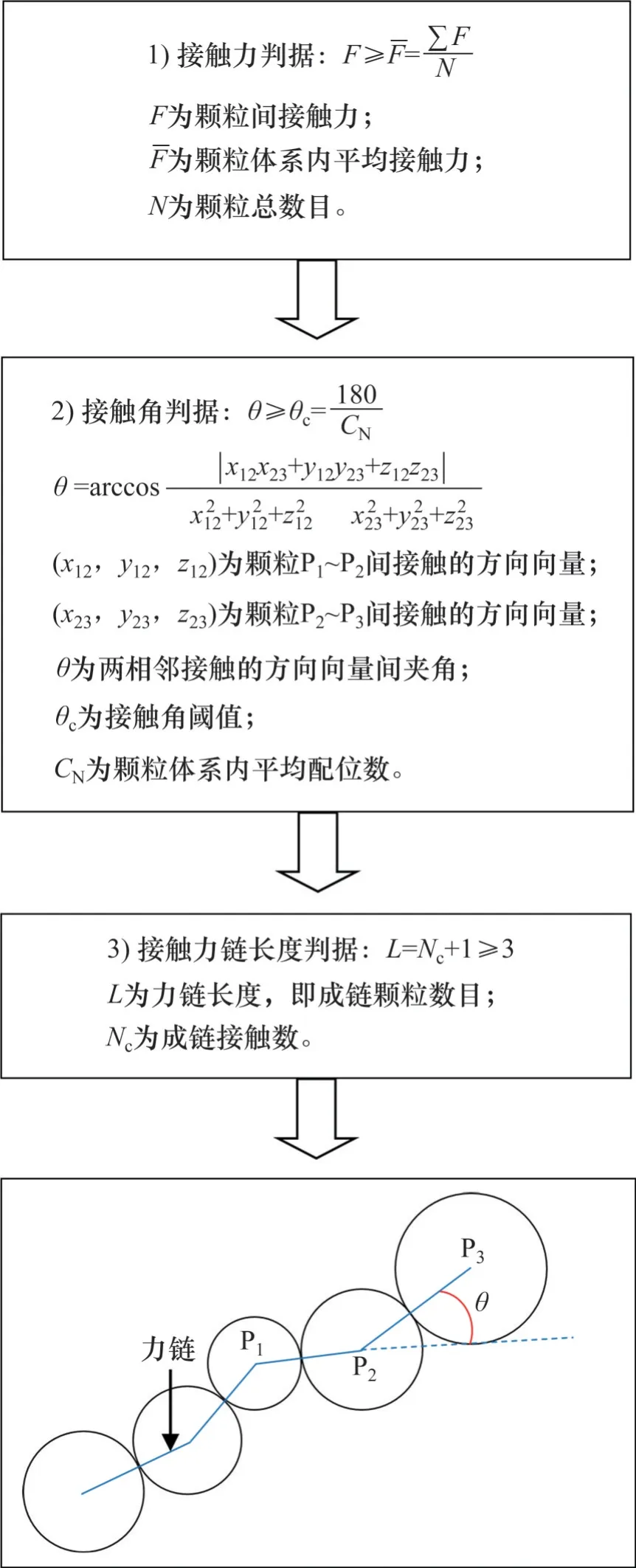
图3 力链识别判据及其示意图Fig. 3 Identifying criterions and sketch of force chain

基于上述三个成链条件，编写三维力链识别FISH 程序，记录不同放矿阶段矿岩颗粒体系中粗颗粒四周局域内颗粒间接触的ID 号、空间坐标、接触方向和强度等信息，即可实现三维力链的自动识别与可视化及其数量、平均强度、准直性、长度与方向等特征参量的提取。

2 不同粗细颗粒粒径比影响下的松动体形态演化规律

基于试验1～8的放矿数值试验结果，探究显著影响松动体形态的粗细颗粒粒径比dc/df。

图4和图5所示分别为不同粗细颗粒粒径比影响下的50 m 高度松动体形态及其最大半径增幅。由图4可知：以不含粗颗粒的试验1以及含有不同粒径粗颗粒的试验5、试验6 和试验8 为例，当不含粗颗粒或粗细颗粒粒径比较小时(dc/df≤5)，松动体整体形态均符合倒置水滴形[30]；当粗细颗粒粒径比较大时(dc/df≥6)，在粗颗粒一侧的松动体形态产生了明显变异，即粗颗粒四周细颗粒出现提前松动的现象。

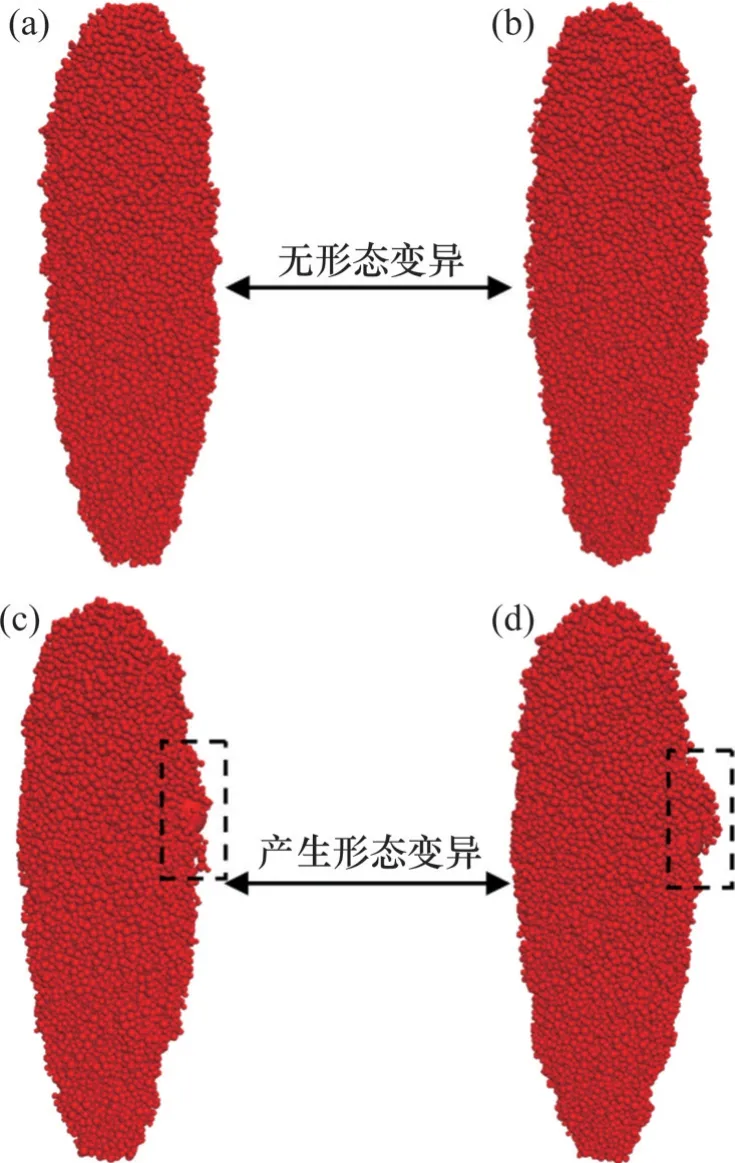
图4 不同粗细颗粒粒径比影响下的50 m高度松动体形态纵剖面图Fig. 4 Longitudinal profiles of IMZ’s shape at height of 50 m under influence of different particle size ratio between coarse and fine particles

图5 不同粗细颗粒粒径比影响下的50 m高度松动体最大半径增幅Fig. 5 Increase of IMZ's maximum radius at height of 50 m under influence of different particle size ratio between coarse and fine particles

从定量角度而言，统计试验2～8中粗颗粒一侧的松动体最大半径，并与无粗颗粒的试验1中松动体最大半径进行对比分析。由图5可知：当粗细颗粒粒径比dc/df≤5 时，松动体最大半径的增幅呈缓慢上升趋势，增幅均小于10%；而粗细颗粒粒径比dc/df≥6 时，松动体最大半径的增幅呈快速上升趋势，增幅均超过10%；当粗细颗粒粒径比dc/df=8时，松动体最大半径的增幅已达32.445%。

图6 所示为试验1 和试验8 松动体高度与粗颗粒一侧的最大半径关系。结合图2中粗颗粒所在空间位置(A点)分析可知：当松动体高度较小即矿岩颗粒松动范围远离粗颗粒所在A点时(如松动体高度小于30 m)，试验8与试验1结果一致，试验8中的松动体高度与其粗颗粒一侧的最大半径均满足倒置水滴理论[30]所述幂函数关系，拟合优度R2达0.996；当松动体高度较大即矿岩颗粒松动范围接近或超过粗颗粒所在A点时(如松动体高度大于40 m)，试验8中粗颗粒一侧的松动体最大半径显著增加，不再满足倒置水滴理论所述幂函数关系。

图6 试验1和试验8中的松动体高度与其粗颗粒一侧的最大半径关系Fig. 6 Relationship between height of IMZ and its maximum radius on side of coarse particle in tests 1 and 8

3 不同位置粗颗粒影响下的矿岩颗粒体系力链演化特征

由前面分析可知：当粗细颗粒粒径比dc/df≥6时，单一粗颗粒的存在将显著影响松动体形态。本节保持粗细颗粒粒径比dc/df=7 不变，首先分析不同空间位置(图2中的A、B、C处)粗颗粒对松动体形态变化的影响；在此基础上，从力链宏观分布、数量、平均强度、准直性、长度以及方向等方面探究不同空间位置粗颗粒对矿岩颗粒体系三维力链演化特征的影响。

3.1 松动体形态变化

基于试验7、试验9和试验10的放矿数值试验结果，得到不同空间位置粗颗粒影响下的30 m 和50 m 高度松动体形态纵剖面图以及松动体高度与其粗颗粒一侧的最大半径关系分别如图7和图8所示。由图7可知：除试验7中的50 m高度松动体形态产生了明显变异外，其余松动体形态均符合典型倒置水滴形。由图8可知：仅当试验7中矿岩颗粒松动范围接近或超过粗颗粒所在A点时(如松动体高度大于40 m)，粗颗粒一侧的松动体最大半径快速增加，其余松动体高度与其粗颗粒一侧的最大半径均满足倒置水滴理论所述幂函数关系，拟合优度R2均大于0.996。综上所述，当粗颗粒位于放矿口垂直轴线正上方(图2 中的B点)或远离矿岩颗粒松动范围的位置(图2 中的C点)时，单一粗颗粒对松动体形态变化无明显影响；仅当一定粒径以上的粗颗粒处于矿岩颗粒剪切带区域[4]即松动体四周区域(图2 中的A点)时，单一粗颗粒的存在才会显著影响松动体形态变化。

图7 不同空间位置粗颗粒影响下的30 m和50 m高度松动体形态纵剖面图Fig. 7 Longitudinal profiles of IMZ's shape at heights of 30 m and 50 m under influence of coarse particle in different spatial positions

图8 不同空间位置粗颗粒影响下的松动体高度与其粗颗粒一侧的最大半径关系Fig. 8 Relationship between height of IMZ and its maximum radius on side of coarse particle under influence of coarse particle in different spatial positions

3.2 力链宏观分布特征

基于试验1(作为对比)、试验7、试验9和试验10 的放矿数值试验结果，利用自编三维力链识别FISH程序，对不同放矿阶段粗颗粒四周局域内(距粗颗粒球心5 m 空间范围)的力链进行自动识别与特征参量统计。图9所示为不同空间位置粗颗粒影响下的粗颗粒四周局域内典型三维力链宏观分布。有两点需要说明：1) 由于试验1中并无粗颗粒，为方便后续与试验7的对比分析，故试验1中识别和统计的是与A点(图2)空间位置最接近的细颗粒四周局域内的三维力链。2) 不同放矿阶段是指四组试验中分别选取连续15 次放矿过程，并且均涵盖如下三个典型放矿阶段：阶段1(矿岩颗粒松动范围尚未波及粗颗粒所在位置)、阶段2(矿岩颗粒松动范围接近和超过粗颗粒所在位置)以及阶段3(粗颗粒进入松动体范围且已发生明显运移)。下文中均使用阶段1～3依次描述上述三个典型放矿阶段。

图9 不同空间位置粗颗粒影响下的粗颗粒四周局域内典型三维力链宏观分布Fig. 9 Macroscopic distributions of typical threedimensional force chains around coarse particle under influence of coarse particle in different spatial positions

1) 对比分析图9 所示的试验1 和试验7 的力链分布可知：在相同放矿阶段，试验7中力链数量明显多于试验1中力链数量，即粗颗粒的存在会起到力链聚集的作用，显著提高其四周力链分布密度。2) 对比分析图9所示的试验7、试验9和试验10的力链分布可知：随着放矿过程推进，试验7和试验9中粗颗粒相继发生移动，其四周力链数量显著减少；而试验10 中粗颗粒始终未发生移动，故其四周力链数量无显著变化。此外，以试验7 的阶段2为例，其力链主要分布于粗颗粒右侧的非松动区域内，而左侧松动区域内几乎无力链分布。综上可得：力链主要分布于矿岩颗粒体系内的非松动区域；当颗粒进入松动区域后，其四周力链数量将显著减少。

3.3 力链数量、强度和准直性变化规律

图10 所示为不同空间位置粗颗粒影响下的粗颗粒四周局域内三维力链数量、平均强度和准直性变化规律。

图10 不同空间位置粗颗粒影响下的粗颗粒四周局域内三维力链特征参量变化Fig. 10 Evolution of characteristic parameters of three-dimensional force chains around coarse particle under influence of coarse particle in different spatial positions

1) 力链数量。由图10(a)可知：四组试验中三维力链数量整体演化规律与图9 分析所得规律一致，此处不再赘述。图10(a)中三条垂直虚线对应的放矿次数为各组试验中粗颗粒开始产生松动的放矿时刻。值得注意的是：① 对比图10(a)中试验1(黑色折线)和试验7(红色折线)，可得：随着放矿次数逐渐增加，两组试验中局域内力链数量差距不断减小，并逐渐趋于50 条左右，即说明随着粗颗粒逐渐进入松动区域，其对力链的聚集效应亦逐渐降低。② 分析图10(a)中试验9(蓝色折线)可得：随着放矿次数逐渐增加，该组试验中粗颗粒及其四周局域内细颗粒均逐渐进入松动区域，其局域内力链数量逐渐趋于0。③ 分析图10(a)中试验10(绿色折线)可得：随着放矿次数逐渐增加，该组试验中粗颗粒及其四周局域内细颗粒始终处于非松动区域内，其局域内力链数量由171条缓慢增加至203条。这是由于矿岩颗粒流动体系内应力由松动区域逐渐向非松动区域转移[31]，故力链逐渐趋向于矿岩颗粒体系内的非松动区域。

由图3中的力链识别判据可知，满足接触力判据的颗粒(强接触颗粒)并不一定能够形成力链。图10(b)所示为放矿过程中力链上的接触数与强接触数之比的演化过程。由图10(b)可知：① 试验7 中力链接触数与强接触数之比远高于试验1中的力链接触数与强接触数之比，说明粗颗粒的存在使其四周游离的强接触颗粒逐渐转化为力链颗粒，荷载被更多的力链承担，亦从另一角度证明了粗颗粒对其四周局域内力链的聚集效应。② 随着放矿次数增加，试验1、试验7 和试验9 中力链接触数与强接触数之比的波动性逐渐增强，其中试验9中力链接触数与强接触数之比的波动性最大，波动范围为0.5～0.9；而粗颗粒始终处于非松动区域的试验10中力链接触占比则无明显波动。

2) 力链平均强度。统计四组试验中局域内力链的平均强度(力链累加强度与力链数目之比)，得到图10(c)所示的力链平均强度演化过程。由图10(c)可知：① 四组试验中力链平均强度随着放矿次数增加均出现不同程度下降，即说明随着放矿过程的推进，矿岩颗粒流动体系内无论是松动区域还是非松动区域，局域力链网络的稳定性均呈下降趋势。② 在各放矿阶段，试验7 中力链平均强度均明显高于试验1，说明粗颗粒可显著提高其四周局域内的力链承载能力，即粗颗粒作为“核心颗粒”在四周局域内细颗粒的包裹下能够形成更为稳定的“颗粒团簇(Clutsers)”结构。换言之，一旦粗颗粒产生移动，在其影响下四周局域内将有更多的细颗粒随之进入松动区域，这也解释了图4中粗颗粒一侧的松动体形态产生变异的现象。

3) 力链准直性。一般而言，力链结构越趋近于直线其稳定性越好，可用力链准直性系数δ对其进行量化研究：

式中：αi为放第i个相邻法向接触间的夹角；Nc为成链接触数；Nac为相邻接触总数目，Nac=Nc-2。

统计四组试验中局域内力链的平均准直性系数(力链累加准直性系数与力链数目之比)，得到图10(d)所示的力链准直性系数演化过程。由图10(d)可知：① 试验1和试验7中局域力链准直性系数无明显差异，变化范围为0.87～0.89，说明粗颗粒存在与否对其局域内力链的准直性无显著影响。② 与力链接触数与强接触数之比以及力链平均强度类似，当粗颗粒及其四周局域内细颗粒均进入松动区域后，其局域内力链的准直性波动最为显著(图10(d)中的蓝色折线)，变化范围为0.86～0.91。

3.4 力链长度变化规律

基于3.1～3.3 节分析可知：当粗颗粒位于放矿口垂直轴线正上方(试验9)时，粗颗粒在放矿初期即产生移动，对整个矿岩颗粒流动过程无显著影响；当粗颗粒位于远离矿岩颗粒松动范围的位置(试验10)，其局域内力链各特征参量均无明显变化且分布规律与放矿初期的试验7中力链分布规律基本一致。因此，本节以试验1和试验7为例，统计两组试验中局域内力链长度即成链颗粒数目N，得到如图11 所示的不同放矿阶段局域力链长度概率分布。

图11 试验1和试验7中不同放矿阶段局域力链长度概率分布Fig. 11 Probability distribution of local force chain length in different draw stages in tests 1 and 7

通过对比两组试验中三个不同放矿阶段局域力链长度概率分布，可以得到如下共性规律：1) 无论是否存在粗颗粒，在各放矿阶段局域内力链概率均随其长度增加而呈负指数函数形式降低，即力链长度越短，其占比越大。2) 从统计意义的角度而言，力链最大长度均不超过10。此外由图11(a)和11(b)可见：在放矿阶段1 和阶段2，试验1中力链长度L=3 的力链占比分别为62.5%和67.6%(浅蓝色区域)，大于试验7 中力链长度L=3 的力链占比(分别为47.2%和53.9%)；而试验7 中力链长度L＞3的力链占比更大一些(黄色区域)，即说明粗颗粒的存在可促进其四周局域内长力链的形成，亦体现出粗颗粒较大的影响范围。在放矿阶段3，试验1和试验7中不同长度力链占比高低的随机性增强，这是由于随着粗颗粒及其四周局域内细颗粒逐渐进入松动区域，局域内长力链不断失稳断裂而形成较短力链。这亦体现出与前两个放矿阶段相比，此阶段粗颗粒对局域内力链的影响程度在不断降低。

3.5 力链方向变化规律

出于对称性考虑，仅统计如图2(b)所示的xz平面内的力链方向。取力链上首尾两颗粒形心连线的方向为该力链方向，力链方向与x轴正方向的夹角为θf。由于θf在0°～360°范围内中心对称，故表示力链方向概率分布时取0°～180°范围。以10°为间隔单位对试验1和试验7中不同放矿阶段局域力链方向进行统计，绘制得到如图12 所示的力链方向概率分布玫瑰图，并利用如式(2)所示三角函数对其进行拟合：

图12 试验1和试验7中不同放矿阶段局域力链方向概率分布Fig. 12 Probability distribution of local force chain direction in different draw stages in tests 1 and 7

式中：a为常数；b为傅里叶系数，通常以b与a的比值(b/a)表示力链方向分布的各向异性程度[32]，比值越大，各向异性程度越低；θn为力链分布的主方向；w为三角函数频率控制参量。

图12 中红色柱状线表示实际局域力链方向统计数据，蓝色轮廓线为基于式(2)的局域力链方向拟合曲线。由图12可见：试验1和试验7中局域力链方向分布均呈近似单花瓣状。其中，随着放矿过程的持续推进，试验1 中概率最大的力链方向范围为65°～75°，其概率变化范围为0.205～0.250；试验7 中力链基本在0°～180°范围内均有分布，概率最大的力链方向范围为55°～65°，其概率由0.134逐渐增加至0.250。综上所述，试验1和试验7中局域力链主方向和该局域颗粒朝放矿口方向移动的趋势基本一致。

为量化两组试验中局域力链方向各向异性程度，统计试验1和试验7不同放矿次数时拟合参数b与a的比值b/a，绘制得到如图13 所示的局域力链方向各向异性程度变化曲线。由图13 可知：1) 试验1 中b/a先减小后增大，其变化范围为1.0～1.6，即局域力链方向各向异性程度整体呈先增大后减小的趋势；试验7 中b/a随放矿次数增加而快速增大，其变化范围为0.6～1.5，即局域力链方向各向异性程度整体呈快速减小的趋势。2) 在放矿阶段1 和阶段2 中，试验7 中局域力链方向各向异性程度明显高于试验1；在放矿阶段3 即局域内颗粒均进入松动范围后，试验7和试验1中局域力链方向各向异性程度逐渐趋于一致。由图12 和图13可知：当粗颗粒及其四周细颗粒未产生松动时，粗颗粒的存在可显著提高局域力链方向各向异性程度，维持更广方向范围内力链的稳定；而当粗颗粒及其四周细颗粒产生松动后，粗颗粒的影响逐渐降低，其局域力链方向各向同性程度逐渐提高，局域力链方向逐渐向放矿口方向集中，驱使该局域内颗粒不断朝放矿口方向移动。

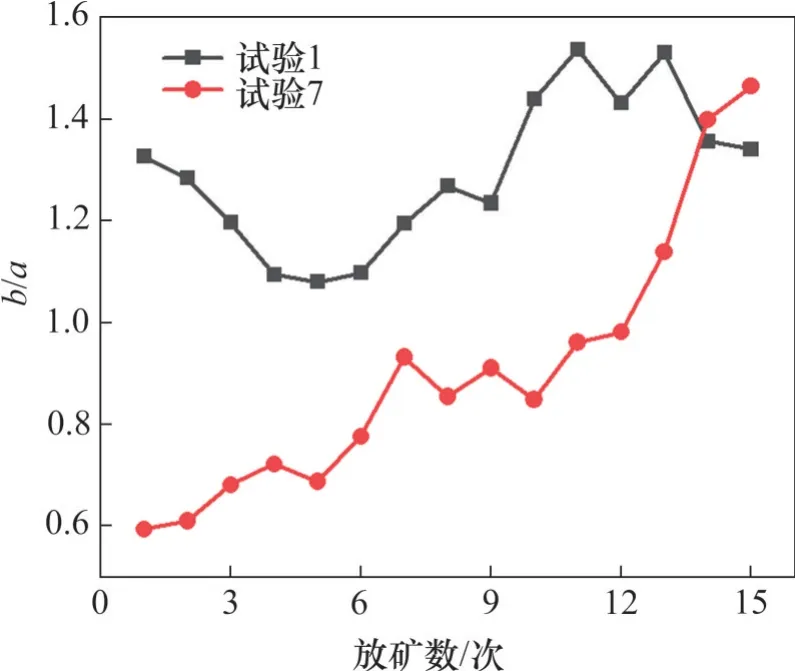
图13 试验1和试验7中局域力链方向的各向异性程度变化Fig. 13 Evolution of anisotropy degree in the direction of local force chain in tests 1 and 7

4 结论

1) 针对0.3～0.8 m 的三维矿岩细颗粒体系，仅当粗细颗粒粒径比dc/df大于6.0 且粗颗粒处于矿岩颗粒剪切带区域时，单一粗颗粒的存在才会导致粗颗粒一侧的松动体形态产生明显变异，引起局域细颗粒的提前移动。随着松动体高度增加，粗颗粒一侧的松动体最大半径显著增加，两者间不再满足倒置水滴理论所述幂函数关系。

2) 三维力链主要分布于矿岩颗粒体系内的非松动区域；当颗粒进入松动区域后，其四周力链数量将显著减少。粗颗粒能够产生力链聚集效应，显著提高其四周局域内力链分布密度、力链接触数占比以及力链平均强度，增强局域力链承载能力，而对力链准直性无显著影响。

3) 无论是否存在粗颗粒，在各放矿阶段局域内力链概率均随其长度增加而呈负指数函数形式减小，力链长度越短，其占比越大；从统计意义的角度而言，力链最大长度均不超过10。

4) 当粗颗粒及其四周细颗粒未产生松动时，粗颗粒的存在可显著提高局域力链方向各向异性程度，维持更广方向范围内力链的稳定；当粗颗粒及其四周细颗粒产生松动后，粗颗粒的影响逐渐降低，其局域力链方向各向同性程度不断提高，局域力链方向逐渐向放矿口方向集中，驱使该局域内颗粒不断朝放矿口方向移动。

5) 一定粒径以上的单一粗颗粒能够显著影响矿岩颗粒流动特性，引起松动体形态产生显著形态，不利于采场结构参数设计和放矿控制。因此，实际崩落法矿山应优化爆破孔网参数和爆破效果，降低大块率。

6) 针对大块率较高的放矿问题，后续作者将基于物理试验和数值试验手段，进一步探究不同粒径、间距和含量粗颗粒影响下的崩落矿岩流动特性、局域小颗粒穿流特性、放矿口堵塞问题以及相应矿岩颗粒体系三维力链演化特征等，丰富和完善现有放矿理论。