基于有效应力法的不排水条件下大直径管桩水平循环动力响应数值分析

曹光伟，欧强，丁选明，周鹏

(1. 重庆大学 土木工程学院，重庆，400045；2. 重庆大学 山地城镇建设与新技术教育部重点实验室，重庆，400045)

大直径单桩基础是海上风电基础的首选[1-2]。随着风机发电功率的不断增大，风电桩基础逐渐大直径化，其直径甚至可达10 m，然而，目前针对大直径海洋管桩的设计方法尚不成熟。我国东部沿海广泛分布深厚软黏土[3]，欧洲现有设计经验无法直接用于我国风电建设，水平动载下黏土大直径管桩的基础变形及承载力特性有待进一步研究。此外，与陆地不同，海床地基始终处于饱和状态，需考虑孔压对土体力学性能的影响：1) 波浪直接作用于海床，在海床表面形成动孔压边界，造成土体强度弱化[4]；2) 波浪作用在桩身，桩周土受到扰动，引起土体孔压累积；此外，随桩径增加，排水路径变长，这种累积更为明显[5]。鉴于此，基于孔压-有效应力分析的风电基础变形及承载力特性研究就显得尤为重要[6-7]。

数值模拟作为重要的研究手段在海上风电基础领域得到了广泛应用[2-4,8-11]，但往往受限于土体本构模型的选择。以ABAQUS 为例，其内置的M-C模型、D-P模型和MCC模型均无法有效地反映土体动力循环特性(如刚度退化和变形累积)，不适用于水平循环荷载下的桩-土非线性问题。此外，该软件的孔压-有效应力分析功能仅限于Standard 静力分析，但Standard 隐式模块对复杂接触和大变形问题(如桩-土接触和桩的贯入)收敛性极差。ABAQUS/Explicit子块非常适用于强烈非线性和大变形问题的研究。目前，ABAQUS/Explicit仅具有总应力分析功能，无法直接进行基于孔压-有效应力的不排水分析。

在以往的不排水分析中，通常采用M-C 模型或D-P模型的总应力进行分析，并取泊松比υ=0.5来考虑不排水过程体变为0的条件。但该方法无法反映动孔压累积及土体有效应力变化情况，不满足有效应力分析的要求。为此，YI 等[12-13]基于MCC 模型开发了适用于ABAQUS/Explicit 的不排水分析VUMAT 子程序。MCC 模型不能有效地反映土体动力循环特性(刚度退化和变形累积)，因此，上述VUMAT 子程序得到土体孔压是不真实的，也不适用于研究海洋大直径管桩基础的变形累积问题。有研究表明，海上风电基础在其生命周期内需要承受约107次负载循环[14]。风电结构对基础刚度和变形有着极其严格的要求，因此，在孔压-有效应力分析条件下，土体动本构模型二次开发对近海风电工程具有非常显著的现实意义。本文基于有效应力原理和黏土有效应力本构模型[15]，开发适用于不排水下的有效应力分析的VUMAT子程序。通过单元试验和离心机试验的验证，发现所开发程序可有效模拟循环动载下土体孔压、累积变形及刚度退化特性，适用于复杂海洋环境荷载下风电基础的受力分析。在此基础上，对水平循环动载下软黏土大直径单桩响应进行数值研究，以进一步揭示水平循环动载下大直径单桩基础变形及刚度退化规律，并给出相应的经验公式。

1 Explicit 模块下不排水条件有效应力分析的数值方法

1.1 黏土本构模型

目前考虑黏土循环特性的本构模型中，以DAFALIAS[16]为代表的边界面模型因参数意义明确和土动力学行为表征合理等优点而备受关注[17-18]。本文采用的模型为ZHOU 等[15]提出的饱和黏土边界面本构模型。该模型可正确预测正常固结与超固结饱和黏土在小应变与大应变下的弹塑性响应及循环荷载下刚度退化和变形累积特征。在本文研究中，弹性剪切行为取决于当前的平均应力p'和当前的空隙比e，弹性应变增量可表示为：

边界面方程是控制土体屈服和塑性模量的关键，在p'-q平面内的边界面方程表示为

式中：F为屈服面函数；n和r为边界面形状参数，当分别取为1.6 和2 时与修正剑桥模型一致；p0为先期固结压力；M为临界状态应力比。

边界面初始大小由p0控制。p0的增量取决于塑性体积应变，并应与修正剑桥模型保持一致。基于非关联流动法则和一致性条件，塑性应变增量可表示为：

1.2 不排水有效应力分析

虽然ABAQUS/Explicit求解得到的均是土体总应力，但总应力{σ}为有效应力{σ′ }与土体孔压{u}之和。因此，有效应力{σ′} 与土体孔压{u} 可分别通过定义土骨架的弹塑性刚度矩阵[D′ep]和水体积模量矩阵[Dw]进行求解，进而求得土体总应力{ }σ，见式(9)～(11)。将上述过程编译到用户自定义的材料子程序VUMAT中，便可实现不排水条件下的孔压-有效应力分析[12]。

式中：{dε}为应变增量；[De]为弹性刚度矩阵；g为塑性势函数；Kw为水的体积模量，本文取2.18 GPa；n为土体孔隙率；E和0分别表示为各元素为1和0的3阶矩阵。

1.3 数值实现

VUMAT子程序的主要任务是基于上一步应力状态及当前给定的应变增量，直接对材料点的应力进行更新并反馈给主程序，无需求解材料的雅可比矩阵[19]。基于此，在VUMAT子程序内部，对所有与土体骨架相关参数均按有效应力状态进行更新求得有效应力，再对孔压进行单独求解，并根据叠加原理求解总应力。对于土体单元的孔压与有效应力输出可通过输出相关状态变量来实现。

数值积分算法是求解土体有效应力的关键。目前，数值积分算法主要有2大类：显式积分算法和隐式积分算法。考虑到对高度非线性问题的收敛性及计算效率，本文采用带有误差控制的改进欧拉应力积分算法[20]来求解积分点处的应力。该算法引入子步概念，根据主程序输入参数的初值，将问题划分成多个子步进行逐步求解。当应力预测值误差满足给定的控制误差时(为尽可能控制求解误差，本文取控制误差为10-6)，对子步中的材料点应力和状态变量进行更新。当所有子步的总步长等于1时，计算土体孔压，更新材料积分点处的总应力和状态变量，并反馈至主程序，具体流程见图1，其中：steptime 为ABAQUS 软件中分析时间；ΔT为子步步长；T为累积步长；Tn为第n次修正后子步步长；ξ为步长修正系数。本程序采用Fortran语言进行双精度编程，共有9 个材料常数和19 个状态变量，可实现显式模块下饱和黏土的完全排水及不排水的动力分析。

图1 VUMAT计算流程Fig. 1 Computing flow of VUMAT

2 数值方法验证

2.1 单元试验

2.1.1 Itsukaichi海洋黏土不排水动三轴

为了评估本程序对饱和黏土静力与动力特性的描述性能，对HYODO等[21]的Itsukaichi高塑性海洋黏土动三轴试验结果进行数值重现。土样直径为50 mm，高度为100 mm，在平均围压200 kPa下固结，其土体参数见表1。三轴不排水单调加载试验为应变控制，加载应变速率为0.001 min-1；单向循环试验为应力控制，加载频率为0.02 Hz。图2 所示为土体单调与循环响应的试验结果与模拟结果对比，其中：pc为初始固结压力；qs为初始偏应力；qcyc和qd均为循环偏应力。由图2 可以看出：偏应力预测曲线与试验曲线基本吻合，VUMAT子程序可较好地模拟Itsukaichi 黏土在单调荷载下不排水过程中的有效应力。对于循环荷载，偏应力计算曲线可以很好地反映黏土在加卸载过程中的位移累积特性，与试验曲线吻合较好。

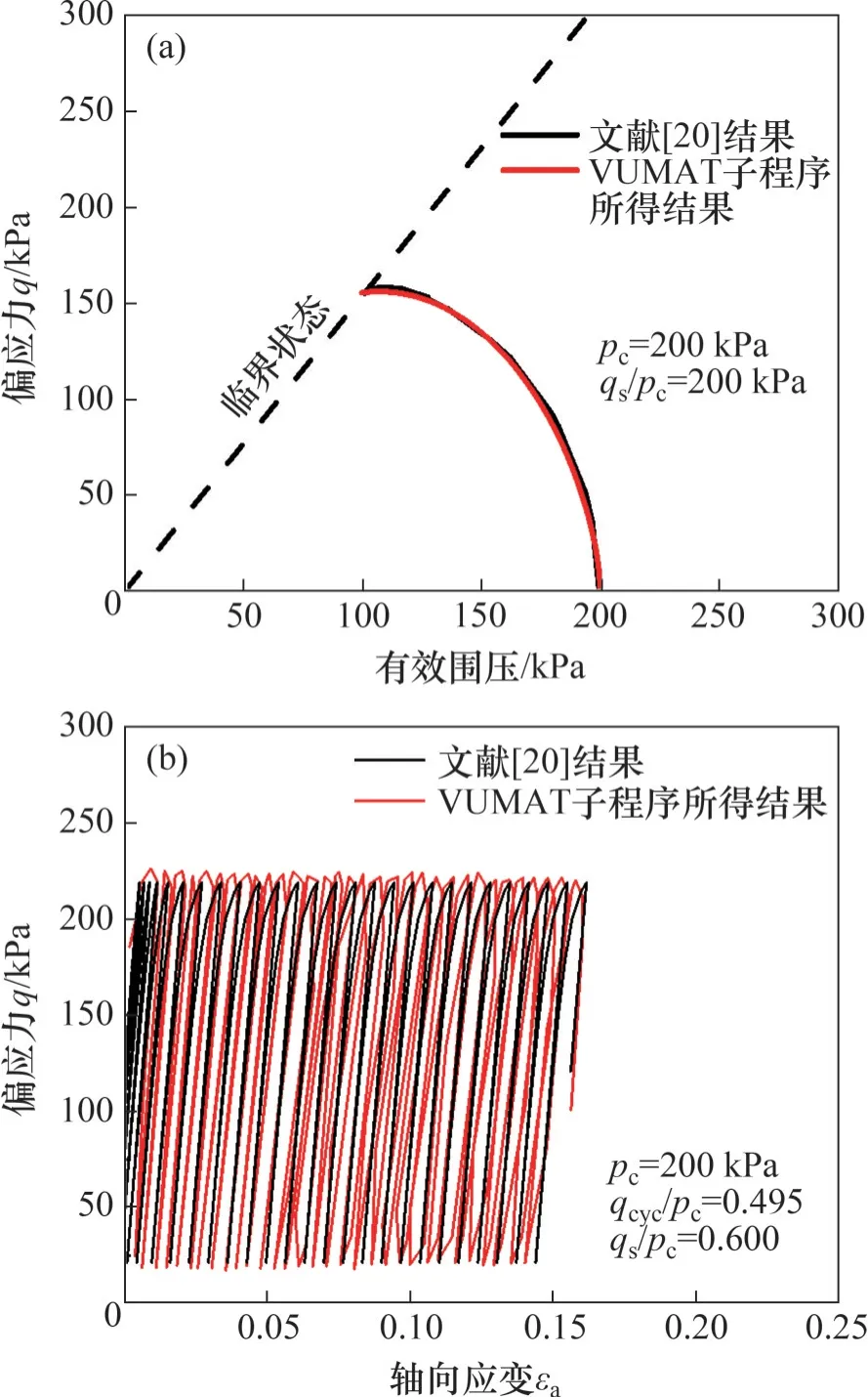
图2 数值模拟结果与试验结果对比Fig. 2 Comparisons between simulation and test

2.1.2 饱和高岭黏土不排水动三轴

为了进一步验证程序的有效性，分别对LI等[22]得出的高岭黏土单向与双向循环三轴试验结果进行了模拟。黏土材料基本参数见表1。试样直径为98 mm，高为110 mm，循环加载频率为0.1 Hz。单向加载试样平均围压为450 kPa，循环动应力幅值为116 kPa；双向加载试样平均围压为350 kPa，循环动应力幅值为130 kPa。图3 所示为孔压-循环次数关系曲线。由图3 可以看出：无论是双向还是单向循环加载，孔压均随循环次数的增加逐渐累积并趋于稳定，数值曲线与试验曲线差异较小，总体基本一致。

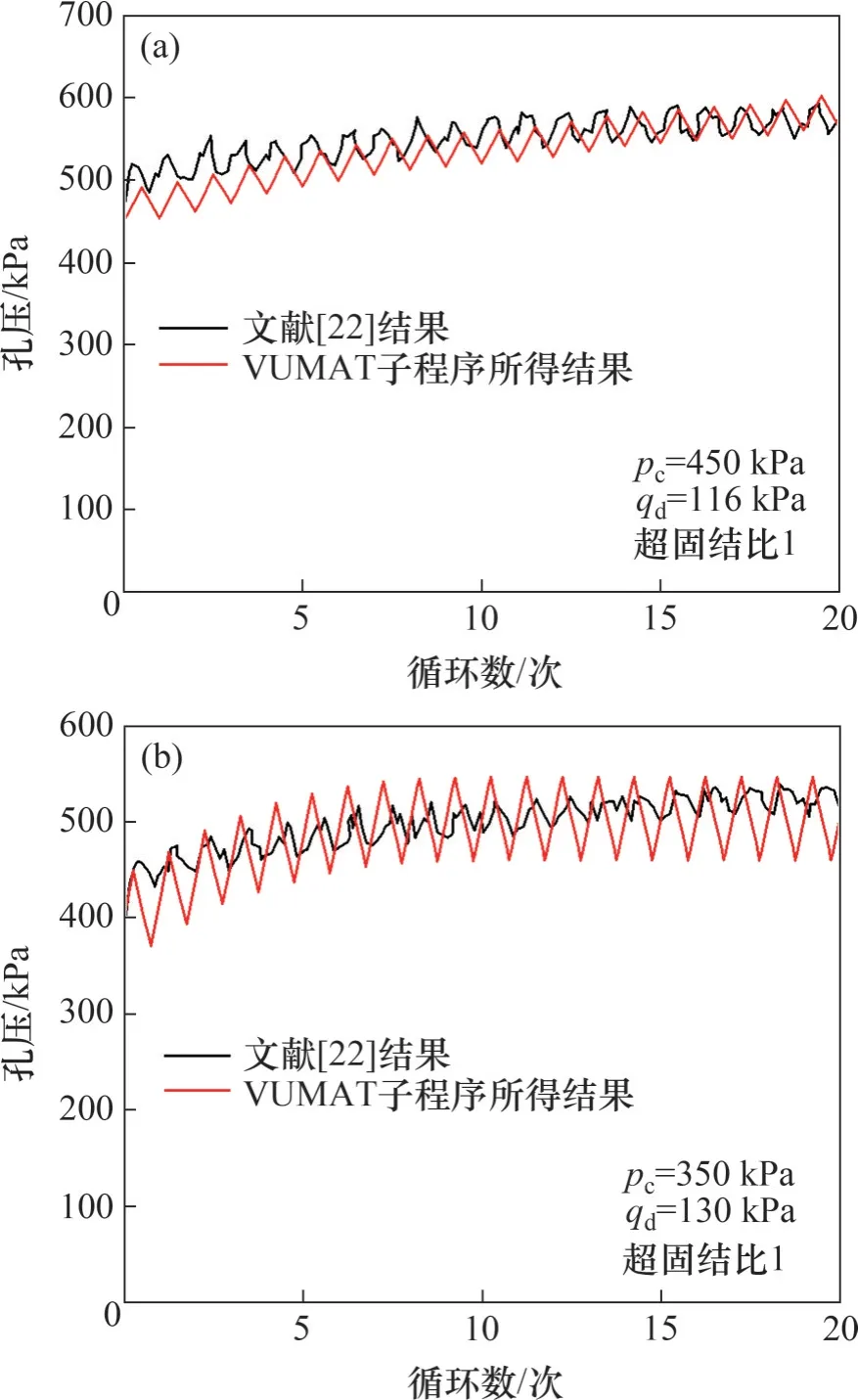
图3 孔压-循环次数曲线Fig. 3 Pore pressure changes versus number of cycles

2.2 单桩离心机试验

为验证本程序对侧向荷载下桩-土不排水行为预测的性能，选取文献[23]中的水平加载单桩离心机试验作为研究对象。试验缩尺比为1∶48，原型桩外径为0.91 m，壁厚为50.8 mm，单桩预埋长度为20.2 m，位于泥线以上的偏心距为4.3 m。试验所使用土为Alwhite 高岭土，其材料特性见表2。原型钢桩密度为7 800 kg/m3，弹性模量为206 GPa，屈服强度为414 MPa。由于模型试验的对称性，取桩土模型的一半进行建模。土体采用增强沙漏控制的C3D8R实体单元建模，单桩采用C3D8I单元。为消除边界的影响，土体半径取20 倍桩径。土体底部采用固定边界，采用外侧弧面约束侧向位移；此外，限制桩和土对称平面的Y向位移。对浅层和靠近桩身(5D内，D为单桩直径)的土体网格进行加密处理，保证桩-土分析的计算精度。采用库仑摩擦法则和考虑接触后分离的硬接触的面-面接触属性表征桩-土界面行为。根据文献[24]推荐公式计算桩-土界面的摩擦因数，本文取0.3。试验循环加载为单向循环位移控制，荷载频率为1 Hz。图4所示为单调与循环荷载下数值与试验结果对比。从图4(a)可以看出：数值曲线可以很好地模拟单桩荷载-位移曲线的加工硬化特性；此外，在深度为6D处的归一化循环P-y曲线的模拟曲线中，随着循环次数的增长，滞回曲线逐渐下移，即存在刚度与承载力退化现象，这与试验结果是一致的。由于文献[23]并未给出高龄黏土的边界面形状参数n与r，因此，本文采用了与修正剑桥一致的形状参数(即n=1.6和r=2)，这可能也是引起计算与试验误差的主要原因。虽然模拟荷载-位移曲线略低估了单桩承载性能且单圈滞回圈面积比试验结果略大，但数值与试验结果的整体趋势基本一致。

表2 Alwhite高岭土参数[23]Table 2 Parameters for Alwhite kaolin[23]

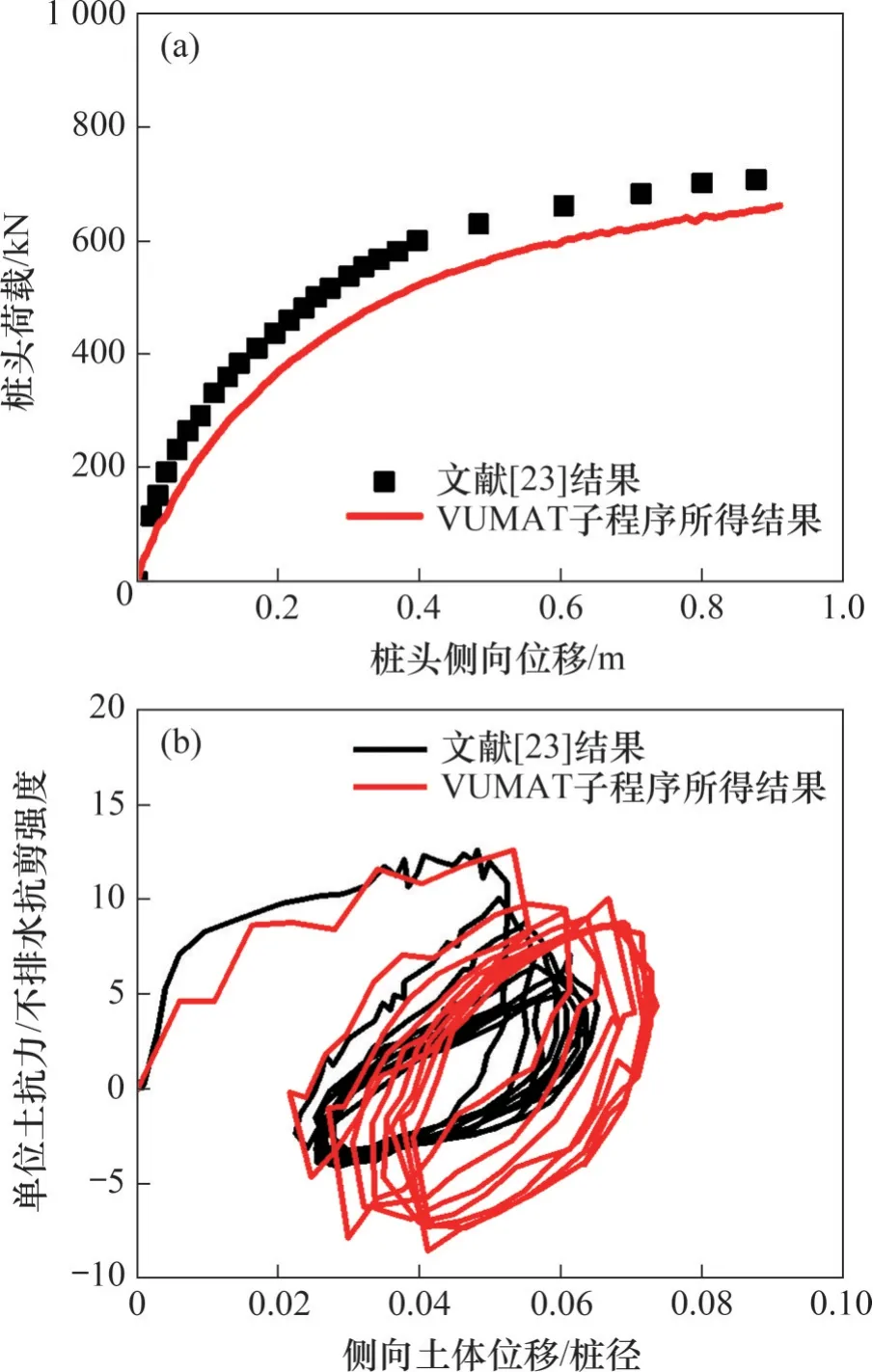
图4 离心机与数值结果对比Fig. 4 Comparisons between centrifuge and simulation results

3 计算结果及分析

在涉及桩-土相互作用的风机动力分析中，常采用子结构法，因此，水平循环荷载下大直径管桩在泥线处的刚度和位移累积规律研究是十分重要的。本节针对不同循环幅值和桩径的大直径管桩，讨论桩的位移累积、刚度退化及孔压累积规律。桩身锚固长度Lp为30 m，壁厚取桩径的1.1%。桩土模型的建模方法与2.2节的相同，土体与管桩的基本材料参数也与文献[23]中的一致。桩顶荷载采用力控制的单向循环水平荷载，加载频率为0.5 Hz，最大循环次数为100 次。桩土相对刚度系数Kr的计算及类型采用Poulos 准则[25](即刚性和柔性桩的Kr上限和下限分别为0.208 0和0.002 5)进行判别。桩研究参数见表3。循环幅值比定义ξ为加载幅值Fcyc比单桩极限荷载Fu，其中极限荷载Fu取泥线0.2D侧向位移所对应荷载[2]。

表3 桩研究参数Table 3 Study parameters for piles

3.1 荷载-位移曲线

图5 所示为循环荷载下桩泥面处荷载-位移曲线(考虑到原荷载-位移过于密集，对其进行了过滤处理)。由图5 可以看出：在整个加载过程中，桩泥线处的侧向位移出现不可恢复的塑性变形，有明显的棘轮效应。循环幅值比对单桩的荷载-位移响应影响非常显著，即循环荷载比越大，由加载引起的土体扰动越大，桩泥线处的位移累积越大。类似地，对于同一循环荷载比下不同直径的桩，桩径越大，累积位移越大。

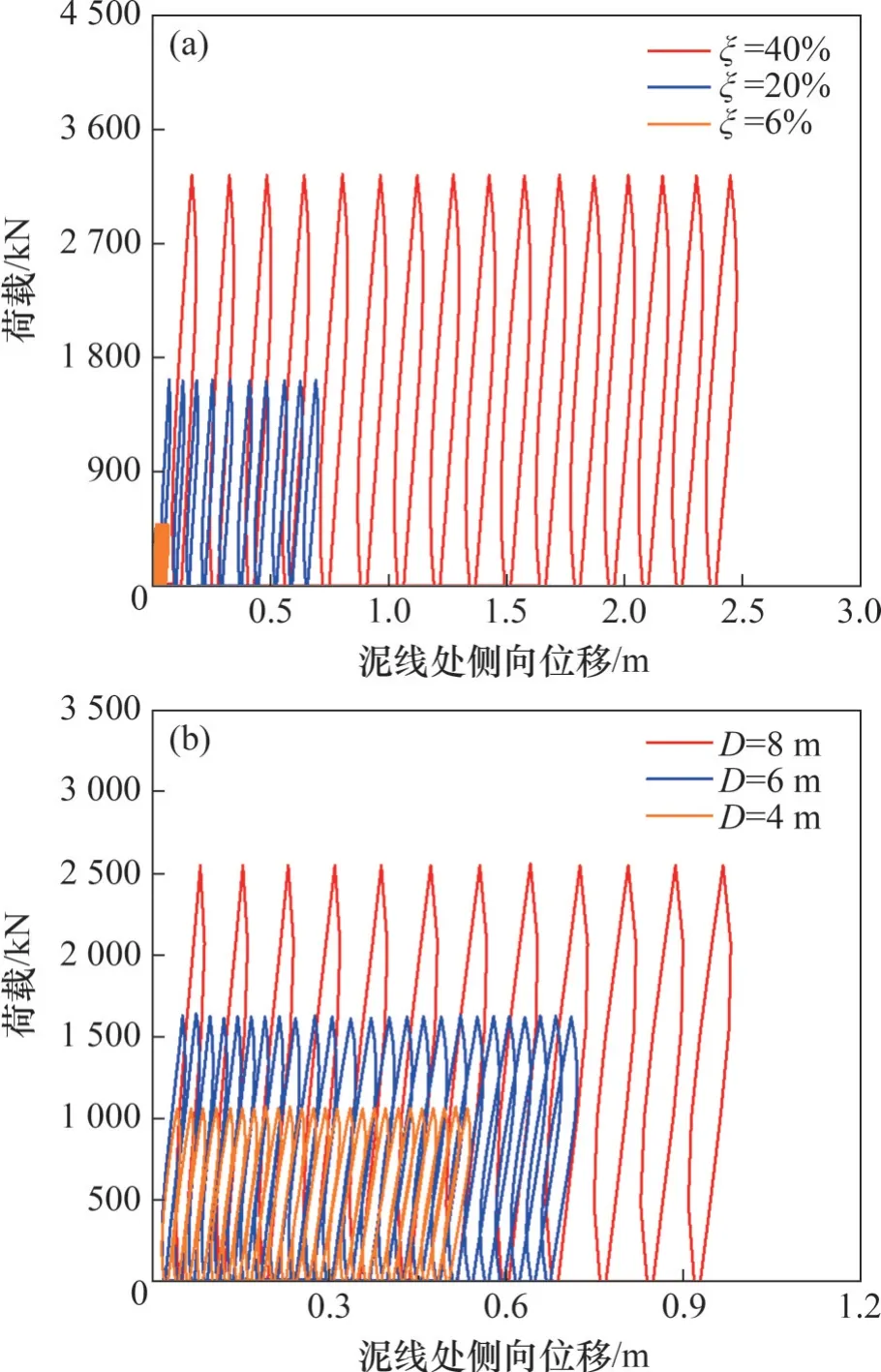
图5 泥线处的荷载-位移曲线Fig. 5 Load-displacement curves at mudline

3.2 累积位移

图6所示为循环荷载下桩泥面处位移随循环次数的演化过程。由图6可以看出：桩泥线处的侧向位移ym随循环次数N的增加而增加；桩的累积位移与循环次数基本呈线性趋势，且在100个循环内无衰减迹象，这与文献[26]中软黏土的离心机试验结果较为类似；另外，随循环幅值的增加，桩泥线处的位移累积速率显著增加；单桩直径越大，累积速率也越大，这与3.1节中的结果一致。使用首次循环卸载后的残余变形(荷载卸至0时的位移)yres,1对残余侧向位移进行归一化处理，结果见图7。从图7 可知：归一化后的累积位移受幅值比控制，但不受直径影响。为预测水平荷载下大直径桩的累积变形情况，采用对数坐标对数据进行拟合。式(12)～(14)为循环次数与累积位移的经验公式，预测公式所得结果与数值结果吻合较好。

图6 泥线处的位移响应Fig. 6 Displacement response at mudline

图7 归一化的累积侧向位移与循环次数曲线Fig. 7 Normalized cumulative lateral displacement versus number of cycles

式中：yres,1和yres,N分别为第1 次和第N次循环的桩泥线处的水平累积位移；Fcyc和Fu分别为循环荷载和静力极限荷载；N为循环次数。

3.3 卸载刚度

对于风机的设计，基础刚度是一个非常重要的参数。定义循环荷载-位移曲线的卸载段最高点与最低点(0 荷载点)之间连线的斜率为卸载刚度。考虑到刚度的退化主要是土体塑性变形引起的，因此，相比于循环次数，桩基础的残余塑性位移更适合用于表征单桩刚度的退化规律。图8所示为归一化后的卸载刚度kun与yres的演化关系曲线。由图8可以看出：在循环初期，桩的卸载刚度随累积变形急剧衰减，然而，随累积变形的持续增长，刚度衰减逐渐趋于平缓，这点与文献[23]的报道一致。此外，不同幅值下的归一化曲线基本一致，归一化的卸载刚度退化受循环幅值比的影响很小；对于不同直径的大直径单桩，直径增加会使卸载刚度衰减更迅速，存在“直径效应”。造成这一现象的原因是：桩径越大，加载引起的土体扰动越大，刚度衰减越迅速。式(15)反映了卸载刚度与累积残余位移之间的经验关系，可有效地反映出单桩直径对于刚度退化的影响，与数值结果整体吻合度较高。

图8 归一化的累积位移与卸载刚度关系Fig. 8 Normalized relationship of unloading stiffness with cumulative displacement

式中：kun,1和kun,N分别为第1次和第N次循环的桩泥线处的卸载刚度；Dref为参考直径，本文取4 m。

3.4 土体孔压

图9 给出了直径为4 m 和8 m 桩在100 个荷载循环后的土体超孔压(状态变量SDV5)分布。由图9可以看到：单桩底部出现明显的超孔压累积，且桩径变大后孔压区域显著增加，尤其是桩底。造成这一现象的原因是：在水平荷载下，刚性桩(或半刚性桩)桩体发生刚体转动，桩底出现“踢脚”位移，对桩底土造成扰动使土体超孔压增大。因此，在工程实际中，应考虑桩底超孔压对土体的弱化。图10 和图11 所示分别为深度3 m 和桩底处(见图9 红色方框)的超孔压与循环次数关系曲线。由图10 和图11 可以看出：加载初期孔压增长迅速，但后期逐渐趋于稳定；另外，荷载增加，桩周土扰动程度加剧，超孔压幅值及其累积显著增加，且初期增长速率增加，但土体超孔压对桩径不敏感。虽然土体超孔压累积量不受桩径控制，但桩径增加后孔压影响区域显著增加(见图9)，这意味着桩径增加会加剧整个土体性能下降，进而影响单桩的受力性能。

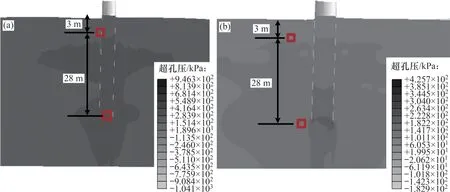
图9 100个循环后的土体超孔压分布Fig. 9 Distributions of excess pore pressure after 100 cycles

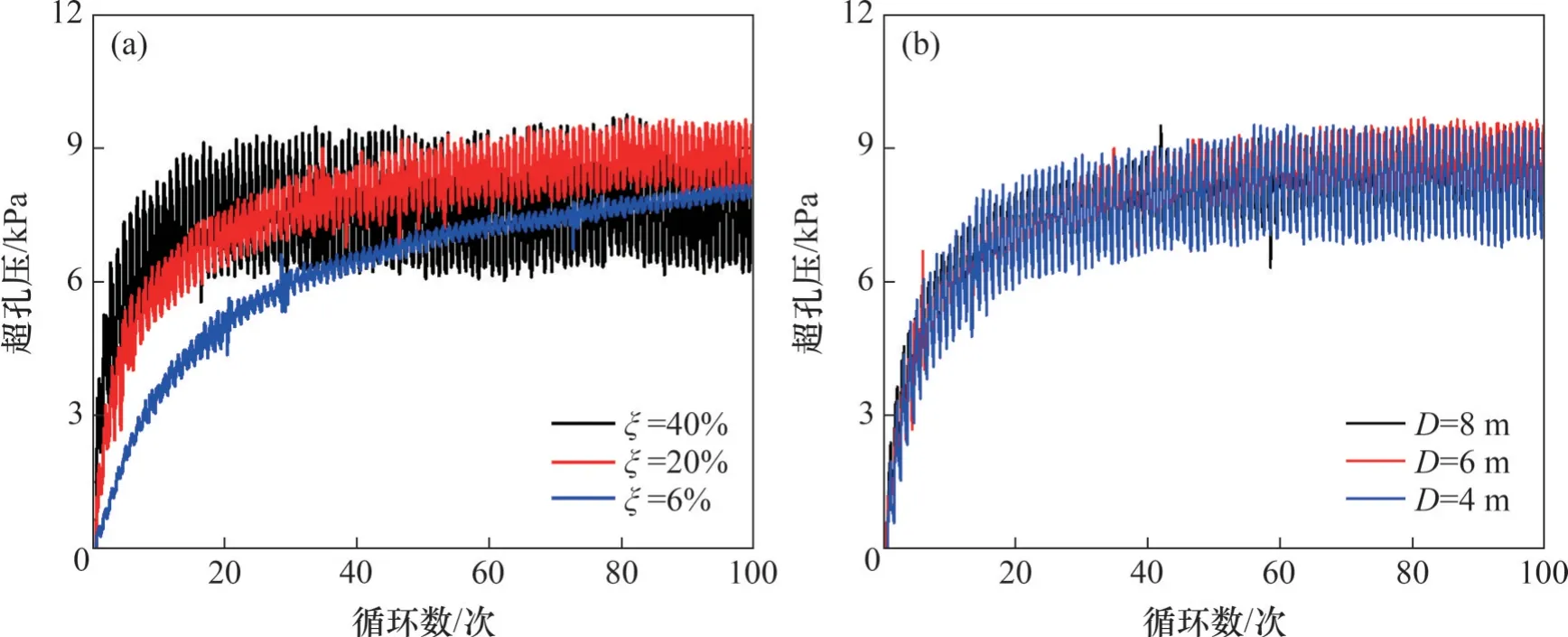
图10 不同加载幅值下桩侧超孔压与循环次数关系曲线Fig. 10 Excess pore pressure changes with number of cycles considering different cyclic amplitudes

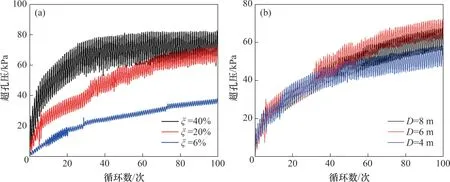
图11 桩底超孔压与循环次数曲线Fig. 11 Excess pore pressure changes with number of cycles at pile base

4 结论

1) 不排水单元试验及水平单桩离心机试验结果表明所开发VUMAT子程序可有效模拟循环荷载下土体在不排水过程中的孔压和位移累积特性及刚度退化行为且具有较高精度。

2) 在水平循环荷载下，桩侧向位移累积随加载次数的增加而增加，有明显的棘轮效应，并与循环次数大致呈线性关系。归一化的位移累积速率会随着循环幅值的增加而显著增加，但与直径无关。

3) 随累积变形增加，单桩卸载刚度衰减速率先大后小，大致呈幂函数关系；归一化的卸载刚度和累积变形演化关系与循环幅值无关，但与直径有关，即卸载刚度的衰减存在“直径效应”，桩径越大，衰减速率越大。

4) 对于大直径海洋单桩，单桩底部会出现显著的孔压累积，工程实际应考虑桩底超孔压对土体弱化的影响。此外，超孔压累积量受循环幅值控制；超孔压对桩径不敏感，但桩径增加后其影响区域显著增加。