三维水下黏质斜坡海床变形冲蚀特征试验研究
窦玉喆,孙淼军,国振,渠立标,朱佳慧,赵洪洋
(1. 浙江大学 建筑工程学院,浙江 杭州,310058;2. 中国电建集团华东勘测设计研究院有限公司,浙江 杭州,311122;3. 海洋岩土工程勘察技术与装备浙江省工程研究中心,浙江 杭州,311122;4. 浙江大学 海洋学院,浙江 舟山,316021)
随着全球气候变化,极端天气频发,海洋环境变得越来越恶劣。海床土体长期承受上部波浪荷载作用,在恶劣海况下容易出现过大变形,诱发海底滑坡,给海洋工程建设带来不利影响,甚至引发重大海洋工程灾害事故,例如1977 年,美国Texaco 公司的海底管道被海底滑坡破坏,造成原油泄漏,产生严重污染[1]。2006年,吕宋海峡发生地震,诱发了多起海底斜坡失稳,致使我国、泰国、马来西亚、越南、韩国和新加坡的海底光缆多处断裂,导致通讯中断长达12 h,造成无法估量的损失[2]。因此,研究波浪作用下海床土体变形失稳特性具备重要的工程价值与意义。
在过去的几十年里,学者们针对波浪作用下海床动力响应进行了大量的研究,主要包括波浪诱发的孔隙水压力响应、海床液化等。SUMER等[3]研究了粉质海床在推进波作用下的响应,例如底砂的输送和海床液化。QI等[4]为了研究波流耦合对超孔隙压力响应的影响,通过一系列大型水槽试验,研究了波浪和水流共同作用下砂质海床的超孔隙水压力响应。SASSA 等[5]通过离心试验研究了波浪荷载作用下海床的液化机理。MIYAMOTO 等[6]结合离心试验结果,研究了推进波作用下可液化土层的变形破坏机理。在理论与数值方面,SUMER 等[7-8]基于Biot 的孔隙弹性理论,在各种假设下建立了波浪-海床相互作用的多孔模型。HSU等[9]提出了有限深海床的Biot方程的解析解,该解析解可以收敛于YAMAMOTO 等[10]和MADSEN[11]提出的无限深海床的解。SASSA等[12]对砂质海床的波浪液化进行了数值研究,并与离心机试验结果进行了比较[5]。同时,人们针对波浪-海床-结构相互作用也开展了许多研究,包括波浪与管线[13-14]以及波浪与桩基[15-18]的相互作用研究。但上述研究均针对砂质海床且忽略了三维特征,对黏质海床的响应特性研究较少,波浪作用下黏质海床的响应特征尚不明确。黏质海床广泛存在于真实的海洋环境中,对其在波浪作用下的动力响应特征的研究同样非常重要。CHEN等[19]基于循环三轴试验,讨论了杭州湾黏土中的孔隙压力发展和耗散特征;杨彦豪等[20]通过空心圆柱扭剪试验研究了波浪荷载作用下软黏土的动力特性。YAMANISHI等[21]研究了试验水槽和潮汐河流中破碎波引起的黏质沉积物冲刷过程。
目前,对于波浪作用下黏质海床的孔压响应以及冲蚀失稳特征的研究较少,且已有的研究大多为单元试验或基于二维条件的模型试验,尚未见波浪作用下三维黏质海床的响应特征研究报道。实际上,近海区域水底一般都不是水平或者均匀坡度的,大多表现为“内凹”或“外凸”。而且,波浪在浅水化过程中对地形变化(包括坡度以及地形形态)较为敏感。DOU等[22]发现在相同波浪参数下,改变海床坡度会导致不同的波浪浅水化特征、破碎类型以及黏质斜坡海床破坏模式。三维海床地形具有更加复杂的波浪场特征,其动力响应特征与二维情况下的不同,从而导致海床土体失稳破坏特征不同。对二维情况下海床的研究结果无法反映真实海洋环境中波浪与三维海底地形的相互作用特征,因此,研究波浪作用下的三维水下黏质斜坡海床变形冲蚀特征具有重要意义。
相比于“外凸”地形,波浪在“内凹”地形传播时波浪有向内凹侧汇聚的趋势,导致波浪在地形内测、坡肩位置和地形较复杂位置表现出更强的非线性。因此,本文针对“内凹”型海床地形开展试验研究,选取舟山某海域作为研究原型,结合现场海底地形,在大型港池中开展一系列试验,研究三维波浪场演化特征以及三维黏质斜坡在波浪作用下的孔压响应特征和冲蚀失稳特征,研究成果可为工程设计提供重要参考及依据。
1 试验设计
1.1 试验设备
本试验在浙江大学海洋学院的大型波流港池中完成,其长为70 m,宽为40 m,深为1.5 m。波流港池可实现潮流、潮位、波浪及泥沙等多因子同步耦合模拟,可采用L 型造波机制造三维波浪。港池工作水深范围为0.2~1.0 m;波周期变化范围为0.3~5.0 s;波高变化范围为0.03~0.30 m。
试验设备还包括波高仪、孔压传感器(PPT)和三维地形扫描仪等,其中,波高仪型号为TCS-1,数据采集采用珠江水利科学研究院研制的高速数据采集器。微型孔隙水压力传感器的量程为20 kPa,表压综合精度为0.2%。试验前,对传感器进行饱和、标定,确保传感器处于正常工作状态。地形扫描采用徕卡ScanStation P30/P40新一代超高速三维激光扫描仪。
1.2 现场条件
试验模拟区域位于舟山某海域,呈“内凹”矩形,长约3.5 km,宽约1.6 km,整个场区内海底地形变化较大,水深在0~80 m 之间,基于现场多波束地形数据建立的等水深线图如图1所示。场区表层和底层的平均流速分别为1.08 m/s和0.78 m/s;表层和底层的最大流速分别为2 m/s 和1.25 m/s。舟山海域为大浪区,平均波高为0.4~1.1 m,最大波高出现在8 月,台风所致波高最大可达11.5 m。因地形复杂,使波浪的运动受地形制约,各处的波浪分布特征不尽相同。海床底质为淤泥质黏土,土体参数见表1。

图1 等水深线图Fig. 1 Bathymetric contour of site

表1 土体参数Table 1 Soil properties
1.3 相似原理
物理模型水槽试验中自由表面重力波的恢复力为重力,而以重力为主要作用力的流动试验参数通常采用弗劳德数Fr相似准则表征。弗劳德数定义如下:
式中,v为流速,m/s;Lc为特征长度,m;g为重力加速度,m/s2。
根据现场地形、波浪资料以及实验室设备条件,采用1∶100几何比例设计港池试验参数,试验比尺详见表2。

表2 试验比尺设置Table 2 Experimental scale set up
1.4 三维海底地形制作
根据目标场区条件,缩尺后的三维地形的长×宽×坡顶高度为38.8 m×12.0 m×0.9 m。试验的三维海底地形采用砖混结构。首先,沿等高线建造砖混框架,然后,在各等高线之间填充废渣,最后,用水泥沿等高线封闭三维地形,尽量保证水体主体与地形之间不发生交换。三维地形在港池中的平面布置及具体尺寸如图2所示。根据现场波浪条件和地形特点确定动床区域位置,如图2中黑色阴影区(长×宽为5.5 m×5.5 m)所示。为预留动床区域,对三维地形施工时,在动床区域的2个侧面以及后面预先按照地形高程设计制作挡墙,以防止土样四处流动。同时,为减少土样用量,在动床区域底部砌筑1个坡顶高度为0.4 m的刚性斜坡体,因此,动床区域坡顶处黏土层厚度为0.5 m。

图2 试验平面布置图(阴影部分代表动床区域)Fig. 2 Test layout plan (shaded part represents live bed area)
1.5 试验用土及试样制备
试验海床由人工制备的结构性淤泥质黏土制成,每次试验需要约10.19 t土样。在制备过程中,首先将土样倒入真空搅拌器中,加水至土样的含水率为液限的2 倍。然后,以30~40 r/min 的转速在真空环境下连续搅拌3 h。为了使土样具有一定的结构性,需要加入土颗粒质量的2%的硅酸盐水泥(#525)[23-24]。将土样、硅酸盐水泥(#525)和水的混合物在真空条件下再搅拌1 h。最后,将制备好的结构性软黏土填筑至三维地形的动床区域,在水下进行自重固结至强度约1 kPa。
1.6 试验工况与传感器布置
本试验仅使用长边造波板造波,三维海床地形试验工况如表3所示,其中,D为坡脚处的初始水深,H为入射波波高,T为入射波周期;g为重力加速度,ζ为波陡,ζ=H/L,L为入射波波长。根据LEMÉHAUTÉ[25]提出的“波浪理论的适用范围”图,本试验入射波主要位于Stokes二阶和三阶波浪理论区,如图3所示。为监测波浪场和海床孔压响应,在港池中布置波高仪并在动床区域沿A-A和B-B断面布置孔压传感器,具体布置方式如图4所示。
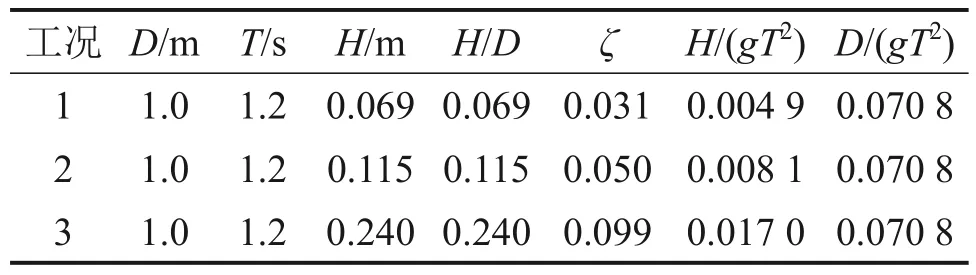
表3 三维海床地形试验工况Table 3 Test conditions of three-dimensional clayey slope seabed

图3 波浪理论的适用范围[25]Fig. 3 Range of suitability of various wave theories[25]

图4 传感器和波高仪布置示意图Fig. 4 Layout diagrams of transducers and wave height meters
1.7 试验步骤
本实验采用从小波高到大波高依次造波的方式进行试验,即首先进行H为0.069 m的波高实验,待水面稳定后再依次进行H为0.115 m和0.240 m的试验。在完成H=0.240 m 试验后进行三维地形扫描。具体步骤如下:1) 根据比例尺在港池中建造三维海底地形;2) 清洗港池;3) 在指定位置安装波高仪;4) 确定试验波高;5) 拆除动床区域地形;6) 饱和并标定孔压传感器;7) 在指定位置安装孔压传感器;8) 制备结构性软黏土;9) 在动床区域内填筑人工制备的软黏土;10) 采用三维地形扫描仪扫描波浪作用前的海床地形;11) 港池注水至完全淹没三维地形,保证海床在水下自重固结至约1 kPa;12) 注水至目标水位,打开数据采集系统,进行造波;13) 停止造波,港池排水,进行三维地形扫描。传感器布置示意图见图4。
2 试验结果及分析
2.1 波浪场特征
图5 所示为波浪在传播过程中的波高沿程变化,其中,x表示波高仪到原点的距离。在A-A断面和B-B断面分别选取距离斜坡坡脚最近的5号和11 号波高仪的位置作为坐标原点,三维地形一侧为正。由图5可知:海底三维地形的存在会导致波浪场具有一定的三维特征,不同断面的波浪特征并不相同。在A-A断面,当波高较小时,波浪在爬坡过程中出现较明显的浅水化现象,波高逐渐增大;当波高H=0.240 m 时,波浪发生明显破碎,导致波高降低。而B-B断面地形较复杂,波浪受地形和反射波影响较大,导致波浪爬坡过程中并未呈现出规则的浅水化特征,在13 号波高仪处波高明显降低。

图5 波浪波高沿程变化Fig. 5 Wave height variation of wave along the path
各阶谐波的幅值随空间变化规律如图6 所示,其中,|An|为n阶谐波振幅(n=1,2,3),Hi/2 为波幅,Hi分别取两断面距离造波板最近的测点(3号和9号波高仪)的波高平均值。从图6可见:与关于水下防波堤或障碍物上波浪传播的结果类似[26-27],高阶谐波分量随着水深的减小而增大,特别是在靠近坡顶的区域,这种现象更明显,这说明波能从主频向高阶转移。在波高H=0.240 m时,三维地形坡顶处的14号波高仪响应出现5阶幅值,如图7所示,由此可知波浪爬坡过程中非线性逐渐增强。

图6 不同入射波下波高的各阶谐波振幅的空间变化Fig. 6 Spatial variation of each order harmonic amplitude of wave height under different incident waves
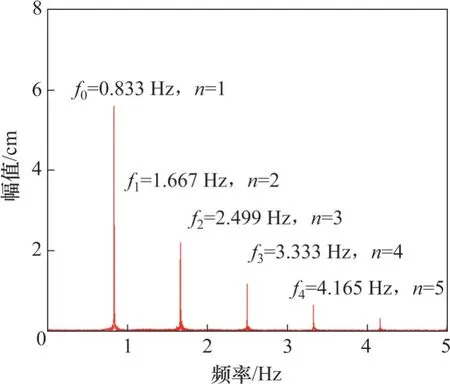
图7 波高H=0.240 m时的频谱特征Fig. 7 Spectral characteristics of wave height H=0.240 m
2.2 斜坡海床孔压响应
波浪与黏性斜坡海床的相互作用非常复杂,是冲蚀、孔压变化以及失稳三者相互耦合直至达到稳定平衡状态的过程。以往研究发现,在波浪荷载作用下,海床孔隙水压力按增长方式的不同可以分为2类,即与瞬时体积应变有关的振荡孔压和由永久压密趋势引起的累积孔压,前者由振荡波压力直接产生,在波浪作用过程中没有累积;后者会引起海床土体内部有效应力逐步减小,对于砂土海床甚至会发生液化现象[28]。
对于波高H=0.069 m 和0.115 m 的情况,海床内部孔压有一定累积,但累积并不明显,因此,本文仅给出了波高H=0.069 m 和0.115 m 时黏质斜坡海床不同位置的振荡孔压幅值随深度变化规律,如图8所示,其中,z为孔压传感器埋深,h为孔压传感器断面处的土层厚度。由图8可知,由于波浪浅水化以及三维化效应,导致不同断面处振荡孔压幅值沿深度变化规律不同。
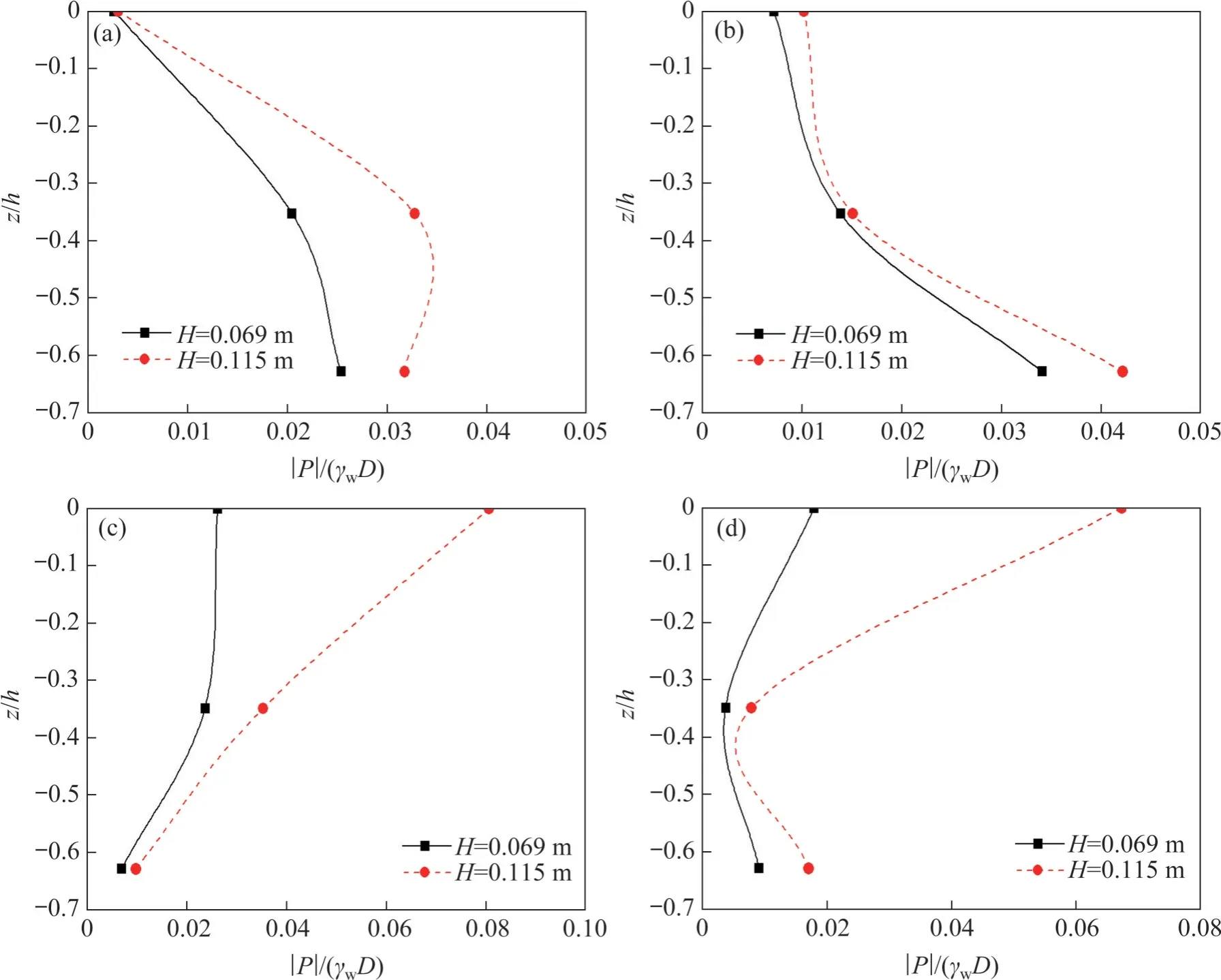
图8 振荡孔压幅值沿深度变化规律Fig. 8 Variation of amplitude of oscillatory pore water pressure with depth
当波高H=0.240 m时,超孔压累积明显,采用信号分析的方法可以有效地提取2种孔压信号的特征。本文选择Daubechies小波对波浪荷载作用下黏质海床超静孔隙水压力响应信号[29]进行分解,进而分离累积孔压分量和振荡孔压分量。图9所示为通过傅里叶变换得到的孔压传感器PPT-1 的孔压响应频谱图。由图9可知:除了与波浪荷载相同的特征频率外,其主要的能量集中在低频区。

图9 孔压响应频谱图Fig. 9 Pore pressure response spectrum
图10 所示为PPT-1 的孔压响应信号通过MATLAB 得到的10 层小波变换分解图,其中,S为原始信号,a10为分解后第10层的低频分量,a10反映了累积孔压分量(低频区);dj为第j层的高频信号,d6反映了振荡孔压分量(高频区)。由图10 可知:通过小波变换可较好地分离累积孔压分量和振荡孔压分量。
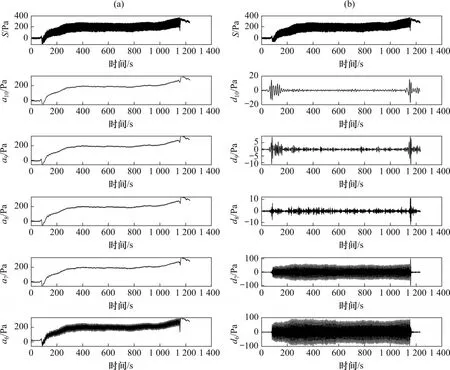
图10 孔压传感器PPT-1的孔压响应信号的小波变换分解图Fig. 10 Wavelet decomposition diagrams of pore pressure response signal of PPT-1
现对波高H=0.240 m时,A-A和B-B断面不同位置的孔压响应信号进行小波变换分析。
图11 所示为波高H=0.240 m 时斜坡土体不同位置处的超孔压累积情况。由图11 可知,在波浪作用的整个过程中,土体表层孔隙水压力基本没有累积;在波浪作用初期,A-A断面处斜坡海床内部的超静孔隙水压力会出现累积现象;在波浪作用过程中,3 号和4 号孔压传感器的响应表现为超静孔隙水压力呈不断增长的趋势,直至加载结束;而6和7号孔压传感器响应则不同,波浪作用初期表现为超孔压累积,随着波浪持续作用,黏质斜坡海床在该位置处受波浪影响较大,海床土体发生冲蚀失稳,导致超孔压逐渐消散,因此,超孔压总体表现为先累积后消散。从图11(c)可见,由于海床土体的冲蚀失稳,7号孔压传感器原本要累积的超孔压在t=500 s 时强制消散,并且随着波浪的持续作用,海床超孔压逐渐消散。
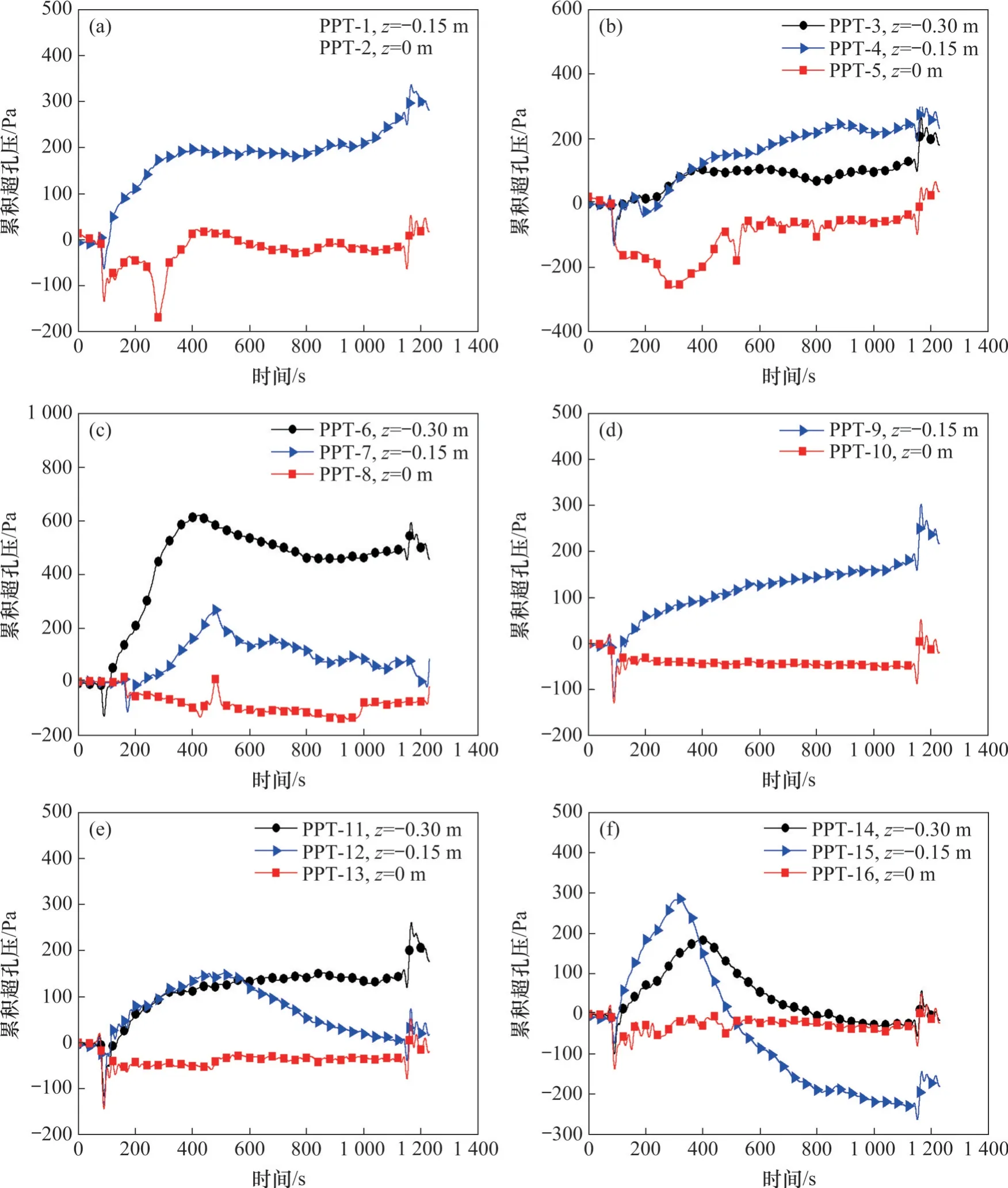
图11 累积超孔压时程曲线Fig. 11 Time history curves of accumulated excess pore pressure
B-B断面处土体内部的超孔压同样由于波浪的循环作用产生累积,但相比于A-A断面消散较明显。与较深处(z=-0.30 m)相比,较浅处(z=-0.15 m)孔压比消散得早且消散较快。斜坡海床A-A和B-B断面的超孔压表现出不同的响应特征,表明由于三维地形的影响,波浪场以及斜坡海床的破坏特征均具有一定的三维特征。通过以上分析可知,波浪场特征、海床内部孔压响应特征以及海床土体冲蚀失稳特征三者相互耦合、相互影响。
2.3 三维地形破坏特征
当波高H=0.240 m时,波浪在坡顶处破碎,波压力在破波区达到最大。在波浪不断地对动床土体拍击、回卷,冲蚀作用明显。同时,斜坡土体在波浪循环荷载作用下,孔压增大,有效应力降低,最终导致斜坡发生破坏。斜坡最终的冲蚀失稳形态如图12(a)所示,波浪作用前后斜坡海床地形如图12(b)和(c)所示。由图12(a)可知:斜坡坡顶位置首先发生冲蚀,然后由坡顶向坡脚方向发生浅层破坏,在靠近坡脚处出现明显的黏土碎屑状堆积;破坏范围集中在动床中间区域,由于地形和波浪的三维效应,海床并未沿着完全平行于动床两侧边界方向破坏,而是斜向潮汐通道。

图12 斜坡海床三维地形图Fig. 12 Three-dimensional topography of sloping seabed
为了更清晰地观察斜坡冲蚀失稳情况,将地形右上角定义为参考原点,分别取距参考原点水平距离1.38、2.75 和4.12 m处的二维剖面,3个剖面分别命名为剖面I-I、Ⅱ-Ⅱ和Ⅲ-Ⅲ。其中,距参考原点1.38 m 和4.12 m 处为地形布置孔压传感器的A-A和B-B断面;距离参考原点2.75 m 处的剖面Ⅱ-Ⅱ为动床区域的中间剖面,如图12(b)所示。3个断面的二维剖面图如图13 所示,其中,红色虚线表示该剖面处原始地形的形态。由图13可知:3个断面的破坏形态并不相同,剖面I-I和剖面Ⅱ-Ⅱ被明显冲蚀破坏,且中间断面Ⅱ-Ⅱ处斜坡土体变形最为显著,距离坡顶2 m范围内的土体由于波浪的冲蚀作用产生了明显的凹陷,而距离坡顶2.5~3.5 m处的黏土碎屑产生了明显的堆积。
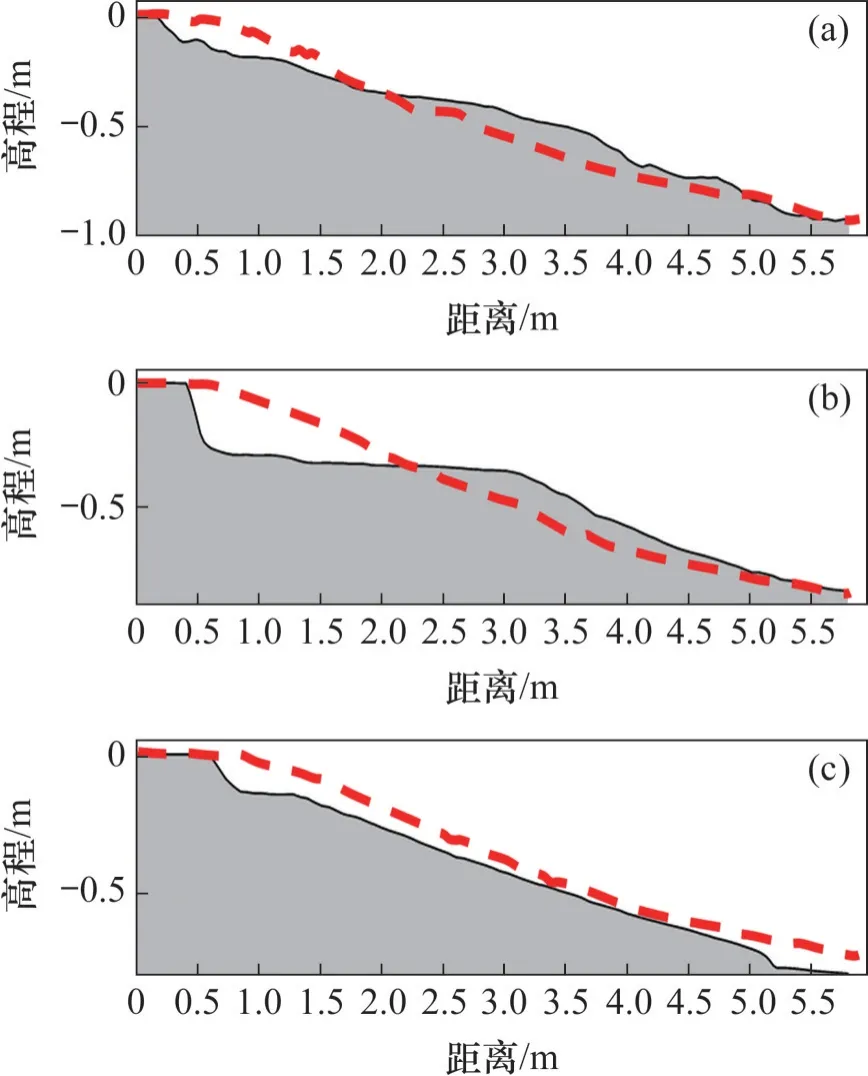
图13 斜坡海床二维剖面图Fig. 13 Sloping seabed of two-dimensional profiles
2.4 三维地形与二维地形的破坏特征对比
为了研究三维地形对海床的影响,同时开展波浪海床相互作用的二维水槽试验,水槽试验的土体与港池试验的相同,试验工况如表4所示。图14 所示为二维水槽试验中不同坡度黏质斜坡的破坏模式。由图14 可见,黏质岸坡与潜坡的破坏模式并不相同,海床坡度对海床的破坏模式影响较大。对于黏质岸坡,波浪在坡上破碎,海床出现冲蚀与块体滑动相互耦合的破坏特征;对于黏质潜坡,海床发生自坡顶向坡脚的浅层破坏。

表4 二维水槽试验工况Table 4 Flume test conditions

图14 二维水槽试验黏质斜坡破坏模式Fig. 14 Failure mode of clayey slope in two-dimensional flume test
通过与二维试验结果比较可以发现,三维水下黏质斜坡的破坏形态与二维水下斜坡的破坏形态并不相同,受三维地形和三维波浪场的影响,海床破坏形态具有一定的三维特征,其冲蚀破坏方向并未在该二维剖面内,而是朝向动床区域左下方的出口(系现场地形的潮汐通道),见三维地形扫测图(图12(c))的箭头方向。综上所述,动床区域发生的破坏是由波压力和波浪破碎的冲蚀效果共同作用导致的,而海床最终的破坏特征对水下三维地形(包括坡度和三维形态等)较为敏感。
3 结论
1) 波浪在三维斜坡地形上传播时会表现出与二维地形类似的、较明显的浅水化现象。但由于三维地形的存在导致波浪场具有一定的三维特征,具体表现为海床的不同断面表现出不同的波浪特征,在坡度较大、地形较复杂处,波浪的高阶分量越明显,非线性也越强。
2) 波浪与黏性斜坡海床的相互作用非常复杂,是冲蚀、孔压变化以及失稳三者相互耦合直至达到稳定平衡的过程。
3) 斜坡海床的孔压响应特征与其冲蚀失稳特征密切相关,高度耦合。三维地形的存在导致海床不同断面处的孔压响应不同,具有较为明显的三维特征。当波高较小时,海床的超孔压没有明显的累积,大多表现为振荡孔压;当波高逐渐增大时,海床内部超孔压在波浪作用初期产生明显累积,土体有效应力降低,随着波浪持续作用,海床土体发生破坏,海床冲蚀失稳特征和程度不同会引起超孔压不同程度地消散。
4) 海床最终的破坏特征对水下三维地形(包括坡度和三维形态等)较为敏感。由于三维地形的存在和波浪的三维化效应,斜坡破坏具有明显三维特征,其并未沿着完全平行于动床两侧边界方向破坏,而是斜向潮汐通道。对于黏质水下斜坡,首先在斜坡坡顶发生冲蚀破坏,然后由坡顶向坡脚方向发生浅层破坏,在靠近坡脚处出现明显的黏土碎屑状堆积。海床的破坏特征与波浪条件、三维地形以及土体性质密切相关。

