经历建构过程 发展符号意识

李玥　孙燕鹏

摘要：发展学生的符号意识是数学教学的重要目标。在课堂教学中，教师要创设合适的情境，设计具有挑战性的数学活动，引导学生经历知识的建构过程，帮助学生在探索中归纳和理解数学模型，并进行解释和应用，进而发展学生的符号意识。

关键词：建构；符号意识；分类活动

“正比例”是北师大版数学教材六年级下册第四单元“正比例与反比例”第二课时内容。本节课，教材注重引导学生从两个相关联的量的变化特征中寻求不变，理解成正比例的量的规律，尝试用数学的眼光观察、分析生活中的数学现象，建立概念模型，发展符号意识。 为了更好地建立“正比例”概念模型，发展学生符号意识，我们通过具体的分类活动，让学生经历正比例意义的建构过程，引导学生从变化中找到不变，建立概念模型。同时，在正比例意义建构过程中培养学生符号意识。

一、 联系生活，理解相关联的量

理解正比例意义的第一个关键是理解“相关联的量”。教师在上课伊始以现实生活素材为教学切入点，创设游戏情境，引导学生初步感知生活与数学中事物之间相关联的现象，为本课的自主探究活动奠定基础。

【教学片段1】

师：同学们，这节课我们先来玩一个小游戏，请你们来扮演小船，按照老师描述的情境去做动作。（小船在宽阔的水面上漂浮着，开始时水面涨高了一些，后来水面越来越高）

师：同学们的表演很精彩，你能根据大家的表演猜一个成语吗？

生：水涨船高。

师：看来河水的变化引起了小船的变化，像这样，一个事物变化，另一个事物也随着变化，我们把生活中的这种变化称为“相关联”现象，变化的这两个量就称为相关联的量。那么，在我们的数学学习中是否有这样的现象呢？

接下来，教师从生活中相关联的量类推到数学上相关联的量，将“比值不变”“积不变”“差不变”以及“无变化规律”4份数学素材一起呈现给学生，要求学生判断每组中的两种数量是否相关联。学生对每组中两种数量的变化规律进行了充分分析与描述，进一步理解了相关联的量的本质意义。这样的设计，有效激活了学生已有的认知经验，有助于学生感受数量之间的变化和关联，从而为后续探索正比例的意义提供了必要的支持和丰富的素材资源。

【教学片段2】

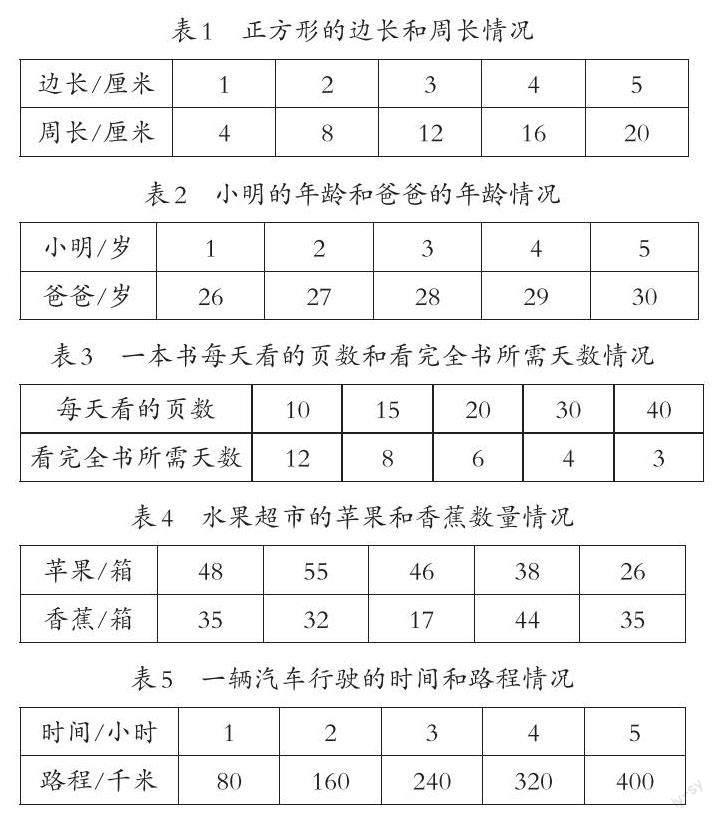
师：请同学们观察表1，你能判断出这两个量是否是相关联的量吗？

生：正方形的边长和周长是相关联的量，因为边长增加，周长也跟着增加。

生：是相关联的量，因为周长随着边长的变化而变化。

师：接下来，请判断下面4个表格中的两个量是否是相关联的量。

生：在表2中，小明的年龄和爸爸的年龄是相关联的量，当小明1岁的时候，爸爸26岁，小明的年龄增加，爸爸的年龄也增加，爸爸年龄随着小明年龄的增加而增加。

生：在表3中，每天看的页数和看完全书所需天数是相关联的量，每天看的页数越多，看完全书所需的天数越少。

生：通过表4可以看出，苹果和香蕉箱数的变化没有关系，所以它们不是相关联的量。

生：通过表5可以看出，汽车行驶的路程随时间的变化而变化，所以路程和时间是相关联的量。

二、借助分类，培养学生符号意识

理解正比例意义的第二个关键是相关联的量“比值一定”。在解决这个问题时，教师先引导学生将几组量分类。学生在辨析过程中依次剥离“无关联”的量和“积不变”的量，除去这两个量对正比例认识的干扰，强化学生对同增同减量的认知。在此基础上，教师又引导学生进行了第二次分类，在同增同减的量中又剥离掉“差一定”的量，最终明晰了构成正比例的一个必要条件——比值一定。

【教学片段3】

师：同学们观察得很准确，在这5个表格中，有一些是相关联的量，还有一些不是相关联的量，还记得表几不是吗？那么，既然表1、表2、表3、表5中的两个量都是相关联的量，你能根据这4组相关联的量的变化特点，对这4个表进行分类吗？请你先独立思考，然后把你的想法在小组内和同伴进行交流。

生：我们小组认为分两类，表1、表2、表5是一类，表3是一类。因为表1、表2、表5中两个相关联的量都是一个量随着另一个量的增加而增加，而表3是一个量随着另一个量的增加而减少。

生：我们组也是这样分类的，我们发现，表1、表2、表5中两个量之间的变化关系就是同增同减，而表3中两个量的变化关系是一增一减。

师：如果我们继续对表1、表2、表3进行分类，你想怎样分呢？

生：我们认为表1和表5分为一类，表2分为一类，因为表1和表5中两个相关联的量的变化规律是一样的，而表2的变化规律和它们不一样。表1中正方形周长总是边长的4倍，表5中汽车行驶的路程总是时间的80倍，而表2不存在这样的倍数关系，爸爸的年龄始终比小明大25岁。

生：我们发现表1、表5中周长与边长的比值始终不变，路程与时间的比值也不变，而表1中爸爸与小明的年龄差是不变的。

在这样具体的分类活动中，学生经历观察分析、分类比较、归纳概括的学习活动和正比例意义的建构过程，感悟到“变化之中蕴含着不变”。同时，教师引导学生根据不变的量抽象出数学关系表达式，培养了学生的数学符号意识。

三、归纳概括，强化学生符号意识

理解正比例意义的第三个关键就是抽象出正比例的字母表达式，建立正比例的模型。当意义揭示后，教师引导学生回顾成正比例关系的例子，概括出它们所具备的共同特点：一是“相关联”，二是“比值一定”。接着，教师让学生尝试用式子表示正比例关系，学生对正比例的表征方式是多样的，不管是文字叙述、表达式概括、字母描述等，都是他们心里自然生长出来的。教师引导学生通过不同关系式的解说与对比，抽象出正比例关系的字母表达式，帮助学生清晰地构建了正比例的数学模型，强化了学生的数学符號意识。

【教学片段4】

师：像表1和表5这样，周长和边长、路程和时间这两组变量，一个量变化，另一个量也随着变化。但不管这两个量怎样变化，它们的比值总是一定的，我们就说这两个量成正比例。

师：你能用自己的话说一说表1和表5这两个情境中的变量为什么成正比例吗？

师：请你根据表6判断购买文具盒的数量和总价是否成正比例，为什么？

师：请同学们观察这几个成正比例關系的例子，其实生活中像这样成正比例关系的例子还有很多，你能用一个关系式来概括吗？

生：两种相关联的量，而且两个量之间的比值一定。

生：[一个量另一个量] =比值（一定），一个量和另一个量成正比例。

生：[AB]=C（一定），A和B成正比例。

师：虽然同学们表示的方法不同，但是都能看出来是两种相关联的量，而且两个量之间的商或者比值是一定的。其实在数学上，我们一般用字母x和y分别表示两种相关联的量，用k来表示它们的比值。那么正比例的关系可以怎样表示？请你试着写一写。

四、在巩固中明辨，深化学生符号意识

为了深化学生对正比例意义的理解，教师在正比例概念模型的基础上，设计了多样的、富有层次的练习，帮助学生打破思维定势：只有满足[yx]=k（一定）的情况，y和x这两个相关联的量才成正比例。这样，可以帮助学生进一步明辨正比例的意义，深化数学符号意识。

【教学片段5】

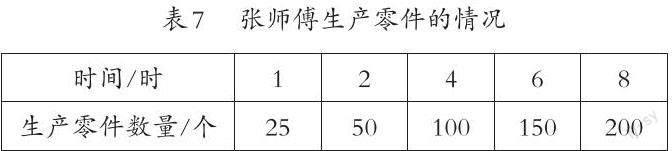
练习：张师傅生产零件的情况如表7。

（1）表格中相关联的量是（）和（），   （）随着（）的变化而变化；

（2）写出几组生产零件数量与时间的比，并计算比值（比值表示什么），你的发现了什么？

（3）生产零件的数量与时间是不是成正比例？ 说明理由。

拓展：其实，古希腊的数学家泰勒斯就利用两个相关联的量成正比例关系来解决实际问题。据说，埃及的金字塔建成1000多年后，没有人能够准确地测出它的高度。人们尝试过很多方法，但都没有成功。泰勒斯用数学方法测量出了金字塔的高度。泰勒斯站在金字塔前，让别人测量他影子的长度。当他影子的长度与他的身高完全相等时，他立刻在金字塔的投影处做一个记号，测量出金字塔影子的长度。这样就得到了金字塔的高度。

延伸：看了古希腊数学家泰勒斯测金字塔的故事后，如果要测量学校教学楼的高度，你能想到什么方法呢？

本节课，教师先从数学素材入手，再抽象出数学关系表达式，最后用字母式来表征正比例，逐层递进，不仅让学生经历正比例意义的建构过程，同时也培养了数学符号意识。

参考文献：

［1］杨强.符号化思想在小学数学教学中的渗透［J］. 辽宁教育，2013（1）.

［2］朱立明，马云鹏.“数学符号意识”研究：内涵与维度［J］. 教育理论与实践，2015（11）.

（责任编辑：杨强）