货物旋转对三向叉车横向稳定性影响及控制策略研究

杨 鹏, 肖本贤, 倪有源, 方紫剑, 肖献强,3

(1.合肥工业大学 电气与自动化工程学院,安徽 合肥 230009; 2.合肥搬易通科技发展有限公司,安徽 合肥 230012; 3.合肥壹恒智能机器人有限公司,安徽 合肥 230009)

0 引 言

随着信息技术、互联网技术和电子商务技术的发展,物流行业也随之迅速发展,叉车作为物流运输环节中的重要设备,其应用领域越来越广阔。其中三向叉车具有独特的货叉旋转及侧移机构,可实现货叉180°旋转及左右侧移堆垛动作,广泛适用于物流、医药、食品及低温冷库现场的高位窄巷道堆垛、装卸、短途运输作业,是实现高货位仓储、提升库容量和提高劳动效率的理想机械。为降低叉车在工作过程中发生倾覆及失稳的风险,国内外研究者对此进行了大量的控制模型、控制算法及控制器方面的技术研究。文献[1]在叉车结构的基础上建立两级侧翻动力学模型,设计了由上层稳定区域识别控制器、基于模型预测控制(model predictive control,MPC)的中层控制器和下层执行控制器组成的防侧翻控制器;文献[2]研究了自动导引叉车(automatic guided vehicle,AGV)原位转向控制策略,采用自适应模糊PID控制算法构建AGV转向控制系统;文献[3]设计一种基于模型预测算法的主动后轮转向控制器,实现叉车的主动后轮转向控制;文献[4]根据重型车辆的三自由度模型设计了一种基于差动制动的模糊滑模控制器,求解出车辆所需的目标横摆力矩,提高了重型车辆在行驶过程中的操纵稳定性和路径跟踪能力。

上述研究考虑了普通叉车合成重心对叉车横向稳定性及纵向倾覆的影响,但并未考虑三向叉车的货叉装载货物旋转引起合成重心变化对叉车横向稳定性的影响。因此,本文首先建立考虑货物旋转情况的三向叉车横向稳定性模型;然后提出一种基于天牛须搜索的粒子群算法(particle swarm optimization based on beetle antennae search,BAS-PSO)来优化线性二次型控制器(linear quadratic regulator,LQR)状态矩阵加权系数的方法,进而设计LQR转向控制器,实现对理想横摆角速度和质心侧偏角的快速跟踪;最后进行双移线换道工况仿真分析,从而验证了所提控制策略的有效性。

本文设计的控制器能有效抑制质心侧偏角的偏移,更好地实时跟踪理想横摆角速度,改善三向叉车在载荷情况下货物旋转造成叉车横向稳定性不足的现象。

1 三向叉车模型

1.1 三向叉车动力学模型

本文所研究的三向叉车的货叉结构如图1所示。三向叉车的货叉结构与普通的平衡重式叉车有所不同,货叉既能装载货物进行横向平移,也能完成180°水平旋转,本文研究工况为货叉装载货物的旋转移动,即研究货物的旋转角速度ω对三向叉车横向稳定性的影响。

图1 三向叉车货叉结构

根据三向叉车的结构特点,将叉车视为车体和货物2个质量块,并作如下假设[5-6]:车辆行驶过程中无垂向运动;忽略车辆悬架作用且保持车辆前进速度恒定;忽略因后轮转向控制车身方向发生偏转所导致的前轮轮胎的随动转向,前轮被动的参与转向;忽略因左右车轮垂直载荷变化所导致的轮胎相应动力学特性变化。本文以叉车水平静止时的空载质心位置为坐标原点,以驾驶员右侧方向设为x轴正向,以叉车直线前进方向设为y轴正向,以空载质心位置垂直向上设为z轴正向,建立的叉车动力学模型如图2所示。

图2 叉车动力学模型

图2中:m为叉车空载质量;q为货物质量;m+q点为叉车装载货物后的合成重心点;R为货物的旋转半径,即载荷中心距;S为货物重心距前轴的水平距离;Lf0、Lr0分别为叉车空载重心距前、后轴的水平距离;a、b分别为合成重心距前、后轴的水平距离;Lq为货物重心距车身纵向中轴线的垂直距离;c为合成重心距车身纵向中轴线的垂直距离;B为轮距;v、μ分别为叉车行驶时的横向速度和纵向速度;γ为叉车绕z轴的横摆角速度;Fyf、Fyr分别为前、后轮所受侧向力;δf、δr分别为前、后车轮转角。

根据图2a中力矩平衡和几何关系[7]可得如下方程:

(1)

根据牛顿第二定律以及图2b的叉车横向动力学模型,可得叉车沿z轴的横摆运动,即

(2)

叉车沿y轴的侧向运动为:

(m+q)ay=2Fyfcosδf+2Fyrcosδr

(3)

其中:ay为叉车沿y轴的纵向加速度;Iz为叉车横摆转动惯量。

Fyf、Fyr、ay具体表达式为:

(4)

其中:kf、kr分别为前后车轮的侧偏刚度;β为质心侧偏角。

在不考虑货物升降的情况下,本文研究在货物的旋转工况下叉车合成重心随时间的变化。根据三向叉车实际使用情况,假定货物的初始位置位于平移臂的最右侧且初始旋转角度为0°,则经过时间t后,货物的重心位置变化如下:

(5)

其中,ω为货物的旋转角速度。由(1)式和(5)式可得时间t后合成重心位置变化如下:

(6)

由于三向叉车在实际运行时车轮转角较小,可对叉车部分参数进行线性化处理,其中可近似取sinδf≈δf,sinδr≈δr,cosδf≈1,cosδr=1,综合(2)～(4)式、(6)式可得考虑货物旋转情况下,三向叉车横向稳定性模型的状态空间表达式为:

(7)

其中

1.2 横向稳定跟踪模型

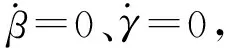
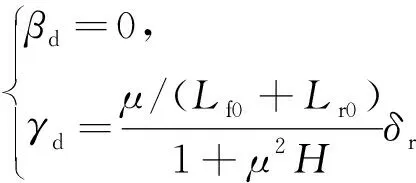
(8)

其中,稳定性因素H为:

2 叉车横向稳定性控制系统设计

2.1 叉车横向稳定性控制原理

本文设计的转向控制策略为后轮转角作为输入信号,经过转向控制器得到前轮控制转角,使得在给定后轮转角输入信号时,前轮同时得到一个修正角度信号,从而提高叉车的横向稳定性。本文设计的叉车横向稳定性控制系统结构如图3所示,主要包括叉车横向稳定跟踪模型、叉车模型、LQR转向控制器和BAS-PSO加权系数调节器。

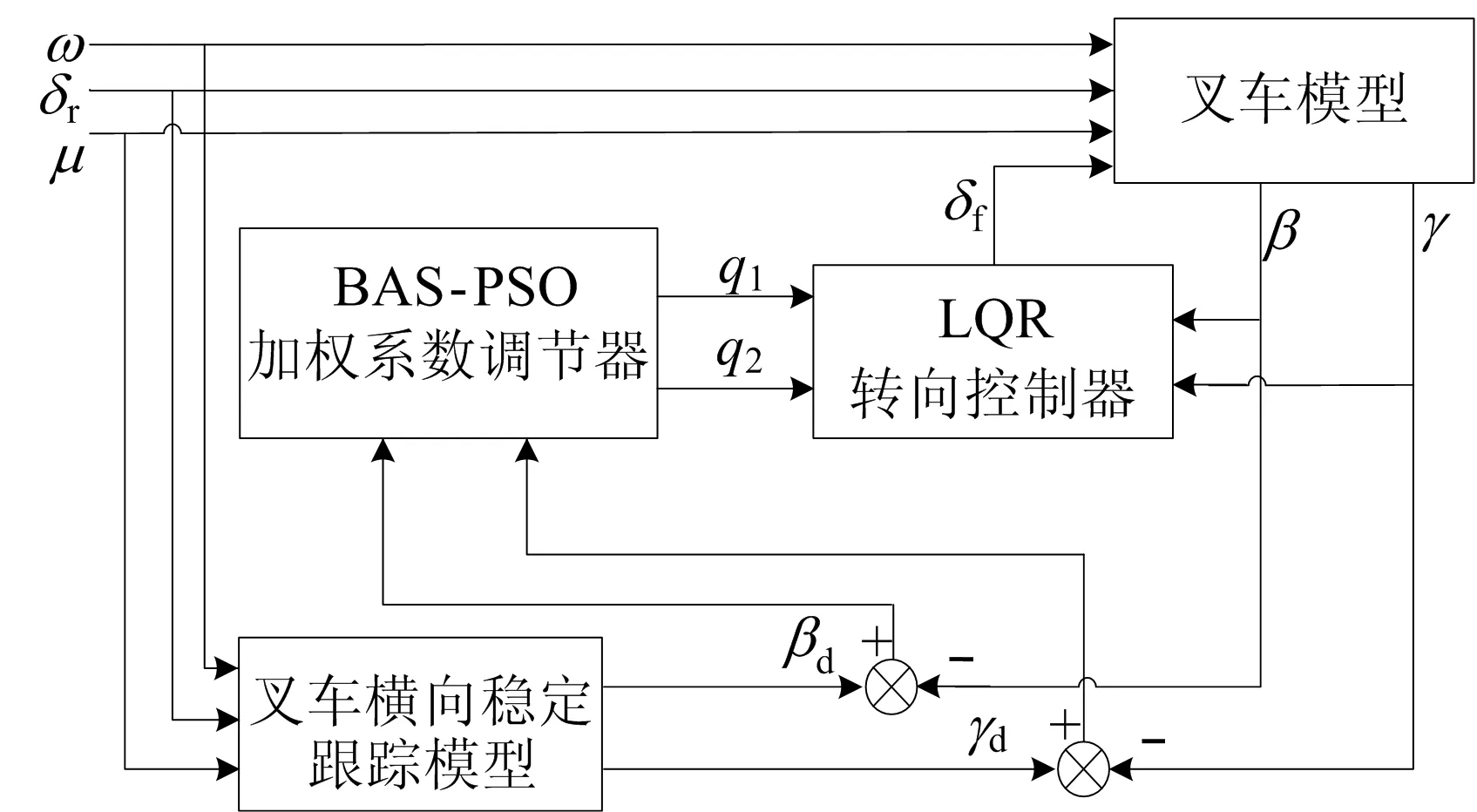
图3 叉车横向稳定性控制原理框图

根据本文设计的转向控制策略,将后轮转角δr、货叉的旋转角速度ω和叉车行驶时的纵向速度μ作为横向稳定跟踪模型的输入量,从而计算出期望的横摆角速度和质心侧偏角;横摆角速度的实际值同期望值之间的偏差和质心侧偏角的实际值同期望值之间的偏差作为BAS-PSO加权系数调节器的输入量,从而在经过寻优运算后得到优化的LQR状态矩阵加权系数q1、q2;LQR转向控制器根据优化后的状态矩阵加权系数得到最优反馈增益Kf,进而得到最优前轮转向角δf,输出给前轮一个修正角度信号,从而提高叉车的横向稳定性。

2.2 LQR前轮转向控制器

根据本文的控制目标,前轮转角作为控制输入,则(7)式可以改为:

(9)

其中

根据LQR最优控制理论[8],三向叉车采用的状态反馈闭环控制系统如图4所示,设叉车前轮优化控制律为:

图4 状态反馈控制框图

u=δf=Kfx

(10)

其中,Kf为状态反馈増益矩阵。为寻找最优前轮转角输入,应该使性能指标函数J取得最小值。

(11)

其中:Q为状态加权矩阵;R为控制加权矩阵。

使上述函数最小化解的计算公式为:

u=-R-1BTPx

(12)

其中,P为Riccati方程的解,计算公式为:

PA+ATP-PBR-1BTP+Q=0

(13)

计算增益后的闭环方程为:

(14)

因此针对本文的线性三向叉车模型,此时有最优前轮转角控制输入,即

u=δf=Kfx=-R-1BTPx

(15)

2.3 基于天牛须搜索的粒子群算法

对于LQR控制器,由于R表示对于执行器u的成本约束,考虑叉车横向稳定性控制的物理意义,可取R=[1]1×1,Q对角阵形式为:

(16)

其中,加权系数q1、q2分别代表对于状态量β、γ的重视程度,LQR控制器的性能好坏很大程度上由Q矩阵的加权系数q1、q2决定。控制器的目标是选取合适的加权系数q1、q2,从而得到合适的反馈增益Kf。但在实际应用中,各加权系数的取值往往来自设计者的经验或大量的实验数据,因此不仅大大降低了工作效率,并且难以达到最优的控制效果。本文将采用BAS-PSO[9-10]作为优化算法,来确定加权系数的选择,以此改善由加权系数选择而导致的最优问题。

粒子群算法(particle swarm optimization,PSO)经过迭代后容易陷入局部最优解,而天牛须搜索(beetle antennae search,BAS)算法中个体初始位置的选择极大地影响了优化的效率和有效性。针对粒子群算法和天牛须搜索算法的不足之处,引入天牛须搜索思想和天牛种群的概念来优化上述算法。

首先需要确定待优化的目标函数,因为本文以横摆角速度偏差和质心侧偏角偏差最小为优化目标,所以根据文献[11]构造如下函数:

(17)

根据(9)式、(12)式、(14)式,可得:

BT(t-τ)P(t-τ)]B2δr}dτ

(18)

其中,P为Riccati方程的解,先给定参数A、B、R、Q,再根据仿真软件中的LQR工具箱计算得出P。由于A、B、R已知,因此目标函数F1、F2中待优化的自变量分别为q1、q2。

取最终的目标函数为:

F=k1F1+k2F2

(19)

根据三向叉车的横向稳定性要求,由于稳定性控制中对横摆角速度的控制效果要求更严苛,在经过多次验证和对比分析后,选定(19)式中k1=0.2,k2=0.8。

2.4 基于BAS-PSO的LQR控制器参数整定

本文基于BAS-PSO对目标函数(19)式进行寻优操作,在保证横摆角速度偏差和质心侧偏角偏差达到横向稳定性控制要求的前提下确定加权系数q1、q2的值。

假设天牛种群中有N只天牛,分别将N只天牛表示为x=(x1,x2,…,xN),根据本文的待优化参数,每只天牛的位置可以定义为xi=[q1iq2i]T,同时也表示一个可能的函数最优解,由于三向叉车的旋转角速度、车轮转角以及车速变化范围通常较小,加权系数q1、q2的取值在某一固定区间内取得,为确定天牛的位置边界,经过LQR工具箱验证测试后,本文选定位置约束条件为:

(20)

(21)

将xi代入本文的目标函数中,得到每个天牛位置的适应度值。随后,天牛的位置发生变化,将天牛位置变化时的速度表示为vi=[v1iv2i]T,本文选定速度的约束条件为:

(22)

速度迭代更新表达式为:

(23)

其中:n为当前迭代次数;r1、r2为[0,1]内的均匀随机数;s=1,2;i=1,2,…,N;根据(17)式、(19)式,Pbesti=[Pbest1iPbest2i]T为第i只天牛的个体极值,将当前种群所有个体的最优解中的最小值作为全局最优解Gbest=[Gbest1Gbest2]T;c1、c2为学习因子常数;w为惯性权重,为加强算法后期的局部搜索能力,其值随迭代过程线性递减,变化规律如下:

(24)

其中,k为最大迭代次数。

本文基于BAS-PSO对上述2个未知参数q1、q2寻优的具体流程如图5所示。位置的更新规律为:

图5 基于BAS-PSO算法的LQR控制器参数整定流程

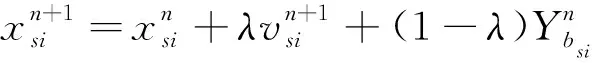
(25)

(26)

(27)

(28)

其中:ξ为步长的衰减系数;d为衰减后的天牛两须之间的距离;e为自然常数。

3 仿真结果及分析

为验证本文提出的三向叉车控制模型和控制算法,根据上文建立的叉车横向动力学模型以及MCA15SQ三向叉车的整车实际数据,并利用仿真软件搭建仿真平台来进行仿真实验,选择在双移线工况下进行仿真。具体仿真模型如图6所示。MCA15SQ三向叉车模型主要参数设置见表1所列。

表1 三向叉车仿真模型主要参数

图6 仿真模型

图6中的反馈增益K=lqr(A,B(:,1),Q,R),取R=[1]1×1,矩阵Q由算法寻优运算求得。首先分析货物旋转对三向叉车横向稳定性影响。设定叉车的纵向速度μ为8 km/h,货叉初始位置位于侧移机构的最右端且初始旋转角度为0°,即货物重心距前轴的水平距离S为0.6 m,货物重心距车身纵向中轴线的垂直距离Lq为1 m,装载货物质量q为500 kg。后轮的最大转角输入幅值为7°(0.122 rad),分别在货物的旋转角速度为0、0.30、0.60 rad/s工况下进行仿真,其仿真结果如图7所示。

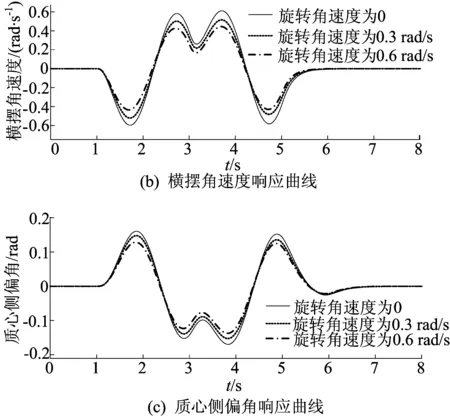
图7 双移线工况叉车位移曲线及仿真结果

从图7b、图7c可以看出,随着三向叉车的行驶和转弯,横摆角速度和质心侧偏角发生相应的变化,且随着货物旋转,横摆角速度和质心侧偏角也出现了一定程度的波动。货物的旋转角速度越慢,叉车的横向稳定性越差,原因在于随着货叉带动货物旋转,叉车的合成重心逐渐向三向叉车纵向中轴线靠拢。在3.8 s,相较于货物旋转角速度为0.60 rad/s时叉车的横摆角速度为0.41 rad/s,旋转角速度为0.30 rad/s时叉车的横摆角速度已经达到0.52 rad/s;在1.8 s,货物旋转角速度为0.60 rad/s时质心侧偏角为0.13 rad,而货物旋转速度为0时叉车质心侧偏角已经达到了0.18 rad。

为了实现对叉车横向稳定性控制,本文设计了基于BAS-PSO优化加权系数的LQR控制器。

在上述双移线工况下,叉车参数设定与上述相同,设定货物的旋转角速度为0.10 rad/s,采用本文所提出的控制策略并与PSO优化加权系数的LQR控制器进行比较。其中:PSO中参数设定分别为c1=c2=1.5,w=0.7;BAS-PSO中各参数设定分别为c1=c2=2,wmax=0.9,wmin=0.4,λ=0.5,ξ=0.95;算法中初始化种群数目N设置为30,迭代次数k为100。2种工况下的仿真结果如图8所示。

图8 不同控制器下的横摆角速度和质心侧偏角响应曲线

从图8可以看出,横向稳定性控制器使叉车在双移线工况下的横摆角速度及质心侧偏角均得到明显的改善。从图8还可以看出,相较于基于PSO优化加权系数的LQR控制器,基于BAS-PSO优化加权系数的LQR控制器具有更良好的实时快速跟随性。在双移线工况下,叉车在无控制状态下的横摆角速度在2.8 s达到峰值0.60 rad/s,质心侧偏角在1.8 s达到峰值0.18 rad,在实际叉车行驶工况过程中,此时叉车已处于横向稳定性不足状态。

采用控制器控制后,叉车横向稳定性不足的情况得到明显改善,在双移线工况下,采用PSO优化控制器时,叉车的横摆角速度在2.9 s达到峰值0.48 rad/s,质心侧偏角在1.9 s达到峰值0.13 rad;采用BAS-PSO优化控制器时,横摆角速度在2.7 s达到峰值0.41 rad/s,且质心侧偏角在1.7 s达到峰值0.08 rad。由于BAS-PSO比传统的PSO具有更强的跳出局部最优解的能力,相较于PSO优化控制器,基于BAS-PSO优化加权系数的LQR控制器能更快速地跟随理想质心侧偏角和理想横摆角速度,使系统的动态控制效果更好,在一定程度上改善了由于三向叉车的货叉带动货物旋转导致横向稳定性变差的问题。

综上所述,基于BAS-PSO优化加权系数的LQR控制器能实现对理想横摆角速度和质心侧偏角的良好跟踪,一定程度上能改善三向叉车因货物旋转造成横向稳定性变差的情况,提高了三向叉车的安全性。

4 结 论

本文根据三向叉车旋转系统的运行特点,首先提出一种考虑货物旋转情况的叉车横向稳定性模型;然后提出一种基于天牛须搜索的粒子群算法(BAS-PSO),优化加权系数的LQR转向控制器跟踪理想横摆角速度和理想质心侧偏角。仿真结果表明,与基于PSO优化加权系数的LQR转向控制器相比,本文所设计的基于BAS-PSO优化加权系数的LQR转向控制器能有效抑制质心侧偏角的偏移,更好地实时跟踪理想横摆角速度,使三向叉车在货叉装载货物旋转时的横向稳定性得到明显改善,一定程度上提高了叉车的工作效率和安全性。