基于WPT 和SVM 的金属薄板损伤信号识别方法*

严宏鑫 朱 平 孙 旺

（中北大学仪器与电子学院 太原 030051）

1 引言

目前，金属薄板由于具有质量轻、强度高、易加工的特性，广泛应用于舰船结构、钢箱梁桥、微反应器等各种复杂的工程领域［1］。但金属薄板在加工和成型过程中易产生内部缺陷问题（如：分层、夹杂物、裂纹等），会降低结构的强度和刚度等力学特性［2］。因此，对金属薄板进行高效、可靠的板材缺陷检测研究已经成为越来越受关注的研究领域。

在超声兰姆波损伤信号识别研究中，微弱信号的特征向量提取常采用经验模态分解、短时傅里叶变换以及小波分解、小波包变换等信号处理方法［3］。其中，小波包变换特征提取方法具有多尺度及多分辨率特性，可以抑制兰姆波回波信号在不同尺度上的噪声，对非平稳信号具有较好的特征表征能力，有效解决多模态中出现的模态混叠问题［4］，适用于复杂工况下金属薄板损伤信号的特征提取。

微弱信号常用的损伤识别分类算法有决策树模型、朴素贝叶斯、神经网络和支持向量机等［5］。其中支持向量机具有高维空间有效的小样本识别优势，需要调节的参数较少，比其他模型方法更适合解决非线性、小样本、高维数据的特征分类问题［6～7］。而模型训练效率受样本数量影响较大，容易陷入局部最优，采用粒子群优化算法对支持向量机的惩罚因子和核函数参数进行寻优，可以有效提升模型的全局收敛能力和局部搜索能力，有助于提高金属薄板损伤识别的分类准确率和鲁棒性［8］。

基于此，本文提出基于WPT 和SVM 的金属薄板损伤信号识别方法，搭建基于超声兰姆波的钢材薄板损伤检测实验平台，采集多种损伤类型的回波信号，经小波包阈值去噪处理后，从时域、频域和时频域多层次构造损伤信号的特征值，在保留原始损伤特征信息的基础上，采用主成分分析方法对特征值作降维处理，有效提高损伤识别效率，然后建立基于SVM 的损伤识别模型进行训练，测试分类出4种损伤类别，验证上述金属薄板损伤特征提取与分类识别方法的有效性。

2 损伤信号特征构建与识别

2.1 基于WPT的特征提取算法

小波包变换（WPT）是在时频域展开的分析方法，不仅可以对包含有大量细节信息的复杂信号低频部分进行逐层分解，而且还能对高频部分做更深入分解，具有良好的时频局部化分析能力［9］。具有典型分解层数的三层小波包分解树结构，如图1所示。

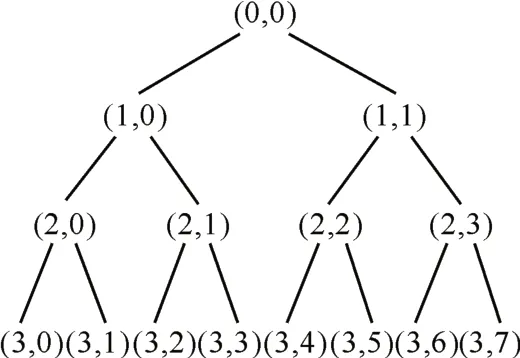
图1 三层小波包分解树结构图

图1 中(i，j)表示小波包分解得到的第i 层的第j个节点，i=0，1，2，3，j=0，1，2，…7。小波包分解树的各个节点都有对应的小波包系数Sij，包含不同频带对应的频率信息。其中，不同分解层数得到的分解信号可由式（1）和式（2）逐层计算得到，小波包分解算法可表示为

小波包重构算法公式为

式中，h(k) 、g(k) 分别表示为高通和低通滤波系数，h′(k)、g′(k)分别表示为高通和低通重构滤波系数，n为采样点数。

本文提出的微弱损伤信号的特征提取算法流程如图2所示。

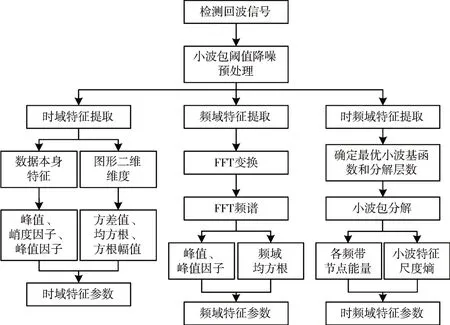
图2 基于WPT的特征提取流程

2.2 SVM基本原理

支持向量机在解决小样本、非线性及高维模式识别中表现出结构简便、泛化能力强等许多特有优势［10］，其结构如图3所示。

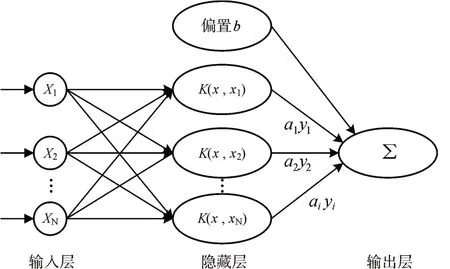
图3 支持向量机结构图

非线性支持向量机通过引入惩罚因子和核函数，将训练样本以非线性映射的方式从原始空间映射到高维特征空间，在高维空间寻找最优分类超平面来逼近目标函数，实现SVM 的分类和回归［11］。其中高维空间的超平面决策函数为

式中，n为训练样本数，训练样本xi所属类别yi，αi为拉格朗日乘数且αi≥0，K(·)表示核函数，b 为偏置因子。

常用的核函数［12］有多项式核函数、Sigmoid 核函数和RBF核函数等。其中，RBF核函数对特征维度和样本数量具有较强的适应能力，因此本文采用RBF核函数，即：

式中，xi、x 为数据样本，γ为核函数唯一超参数，||·||表示向量的范数或模。

2.3 基于WPT-SVM损伤识别流程

基于WPT 和SVM 的损伤识别过程主要包括：数据预处理阶段、损伤特征提取阶段、模型参数优化及损伤识别阶段。图4 为金属薄板损伤信号分析流程图，具体步骤如下：

图4 金属薄板损伤信号分析流程

1）为了消除数据异常点对模型训练的影响，对回波信号作幅值归一化处理，采用小波包阈值降噪作滤波预处理，并对回波信号进行小波包分解。

2）在时域中，选取峰值、峭度因子、峰值因子作为第一至三类特征值（U1～U3），从信号图形角度选取方差值、均方根、方根幅值作为第四至六类特征值（U4～U6），构建出第一部分特征向量；在频域中，对回波信号作FFT 变换进行频谱分析，选取峰值、峰值因子和均方根作为第七至九类特征值（U7～U9），构建出第二部分特征向量；在时频域中，对回波信号进行小波包分解，选取各频带节点能量和小波特征尺度熵［13］作为第十至二十五类特征值（U10～U25），构建出第三部分特征向量；对上述25维特征值组成的损伤特征向量U 作主成分分析（PCA）特征降维处理，并建立样本数据集。其中，特征向量U如式（6）所示。

3）将样本数据集划分为训练样本集和测试样本集，并构建SVM 模型，采用PSO 算法对惩罚因子、核函数进行参数寻优。经过多次训练得到SVM损伤识别模型，对多种损伤类型进行识别分类，并输出识别结果。

3 实验平台搭建

3.1 钢材薄板损伤检测实验

实验平台仪器包括：任意函数发生器、功率放大器、数字示波器等。实验采用500mm×500mm×1.5mm的钢材薄板，主要参数详见表2所示。

在不同钢材薄板的中心处分别人为加工两种模拟损伤的尺寸如下：

孔洞损伤尺寸：φ2mm×1mm；

槽形损伤尺寸：4mm×1mm×1mm。

表1 钢材薄板主要参数

将激励信号通过功率放大器放大后，加载至压电陶瓷片振动待测钢材薄板。接收端压电陶瓷片采集到带有损伤特征的兰姆波信号，通过导线连接到数据采集卡，并由示波器输出信号波形。

3.2 兰姆波激励信号选取

设定采样频率为100 MHz，采样点数为15000个，激励信号则选用经窄带激励（Hanning 窗）调制的、额定激发频率为300 kHz 周期为5 的正弦波信号，如式（7）所示：

式中，激励信号的频率f0，激励信号的周期数n，时间t。

4 结果与讨论

4.1 时域波形分析

同种类型回波波形具有相似性，图5 展示了钢材薄板在无损伤、孔洞损伤、槽型损伤、焊点情况下的典型回波时域信号。

图5 回波信号时域图

4.2 小波包分解结果

本文根据基于变异系数指标融合的复合指标评价方法［14］确定最优分解层数和小波基函数，选取db12小波对回波信号作3层小波包分解，实现对回波信号的小波包阈值降噪。回波信号小波包分解结果如图6 所示，其中纵轴S0 表示回波时域信号，S30～S33 分别表示小波包分解后前四个频段的节点系数。

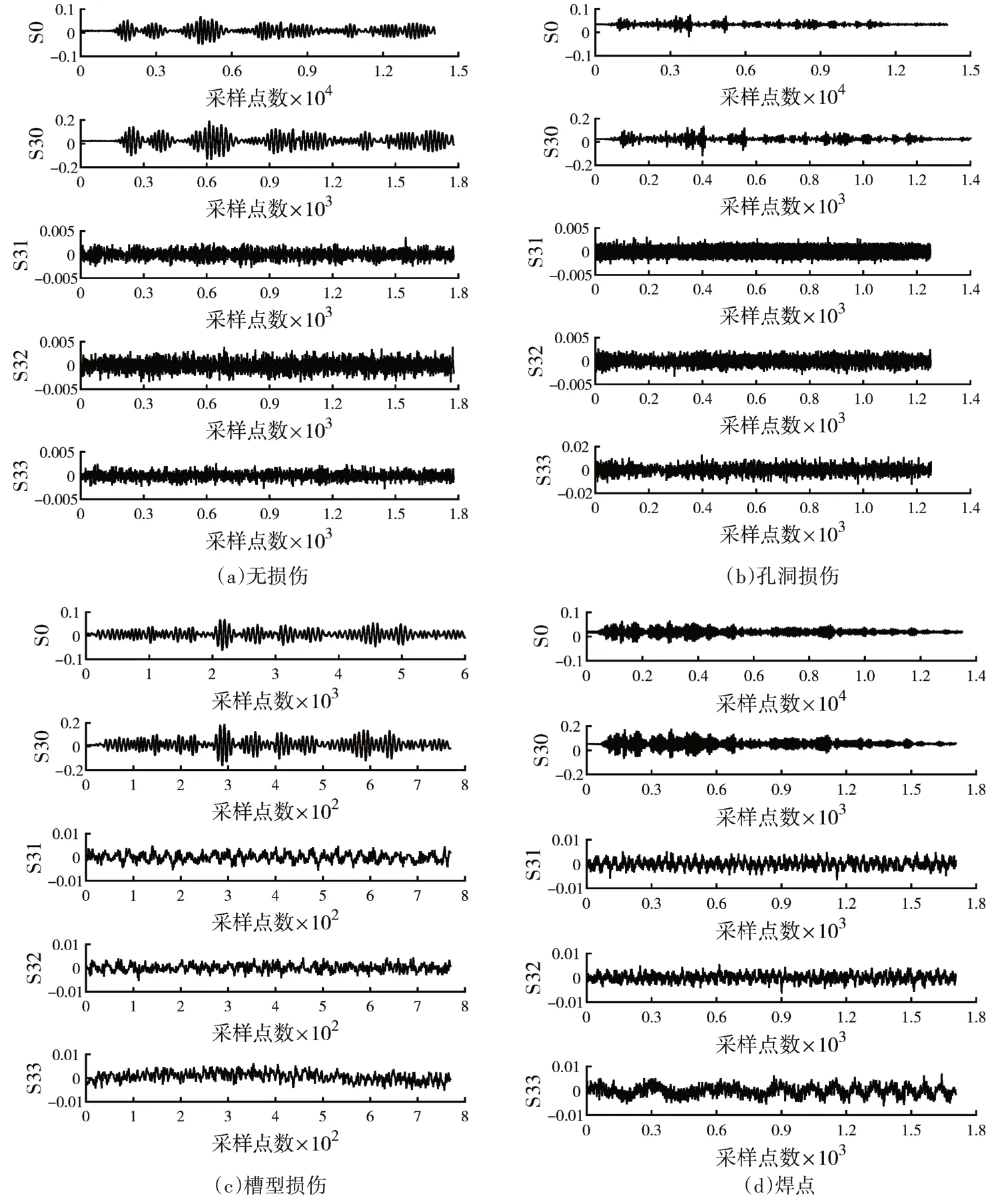
图6 回波信号的小波包分解结果

4.3 构建特征向量

回波信号经小波包阈值降噪后，根据基于WPT 的特征提取方法，在时域、频域和时频域构建损伤特征向量，并对其包含的25 个特征值进行主成分分析。其中，时域、频域和时频域特征参数平均值汇总在表2～5中。

表2 时域特征参数

表3 频域特征参数

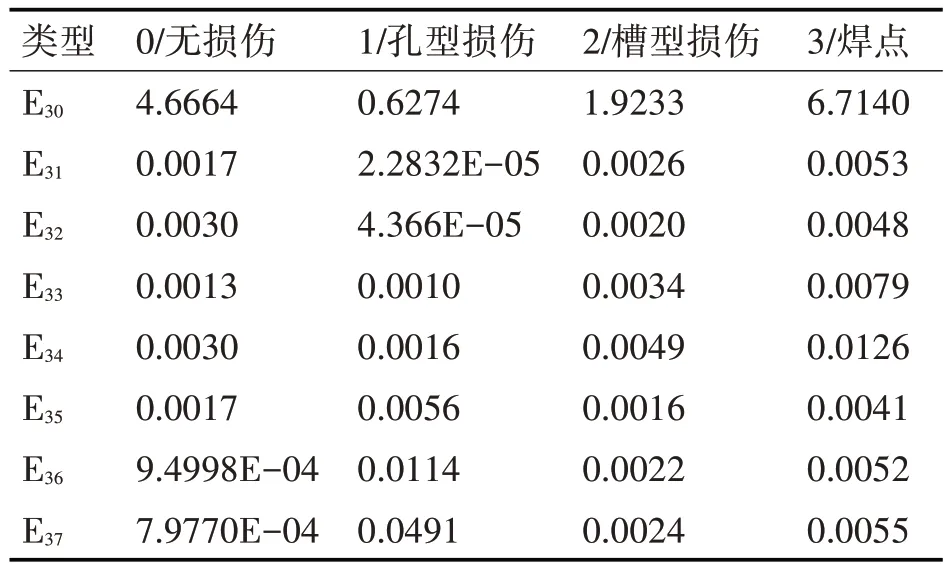
表4 时频域特征参数（各频带节点能量）

表5 时频域特征参数（小波特征尺度熵）

在主成分分析中，当前k 个主成分的累计贡献率超过90%时，则认为这k 个主成分能够代表原信号的绝大部分特征信息［15］。主成分贡献率及累计贡献率如表6 所示，贡献率高的主成分主要集中在前3 个主成分中，其中第一主成分、第二主成分和第三主成分的贡献率分别为34.55%、43.36%和15.41%，而剩余的22 种成分贡献率很低，属于冗余信息，应对其进行剔除。因此，选取特征向量的前3个主成分构建样本数据集。

表6 主成分贡献率及累计贡献率

4.4 SVM分类结果

根据小波包变换-支持向量机损伤识别流程，随机选取200 组损伤信号样本作为样本数据集，其中164 组作为训练样本，剩余36 组作为测试样本，并采用PSO 算法优化SVM 模型参数。图7 为PSO算法迭代次数与适应度值关系曲线。经过多次训练，将测试样本输入到训练好的SVM 模型中进行识别分类，根据输出的标签判断损伤类型，并设定无损伤信号的标识类别为0，孔洞损伤信号的标识类别为1，槽型损伤信号的标识类别为2，焊点信号的标识类别为3。

图7 PSO迭代次数与适应度值关系曲线

从图7 可以看出，随着粒子种群速度和位置的不断迭代进化，最佳适应度值逐渐增大，且在第51次迭代进化时收敛至96%，此时得到最优惩罚因子C和核函数参数γ分别为0.3952和8.1476。将测试样本输入至优化后的SVM 模型进行损伤识别分类，单次随机样本SVM 模型损伤识别分类结果如图8 所示，经过计算，该模型损伤类型识别准确率为91.67%，识别分类效果良好。

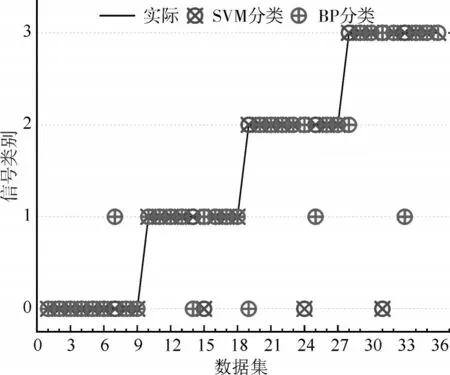
图8 单次随机样本SVM和BP神经网络的分类结果

为了进一步验证本文提出的SVM 模型的识别分类能力，将相同的36组测试样本输入到3层神经网络结构的BP 神经网络中进行分类对比，损伤分类结果展示在图8 中，可以计算出BP 神经网络的分类精度为83.33%，识别准确率较低。

5 结语

本文提出一种基于小波包变换和支持向量机的钢材薄板的损伤信号特征提取与识别方法，通过搭建基于兰姆波的多目标损伤识别实验平台，对产生的回波信号进行小波包阈值去噪预处理，从时域、频域和时频域3 个层次构建出回波信号的特征量，通过主成分分析法降维处理提取出损伤特征向量，作为样本数据集输入支持向量机模型识别分类出4 种损伤类型，与BP 神经网络相比，支持向量机模型识别方法分类精度高，具有较好的分类性能，验证了钢材薄板损伤识别模型的有效性和准确性。