基于简化模型马尔可夫法的核电厂仪控系统可靠性评估方法
张 庆,魏新宇
(西安交通大学 能源与动力工程学院,西安 710049)
0 引言
IEC 61508[1]推荐了几种用于评估核电厂数字化仪控系统(DCS,Digital Control System)可靠性的计算方法,其中包括马尔可夫方法。马尔可夫方法是利用马尔可夫链,表示出系统的状态转移图,可完整表达出系统的全部状态,包括正常状态、降级状态和失效状态。马尔可夫模型中的一个状态转移到另一个状态的概率仅仅取决于系统当前的状态,与其历史状态无关。马尔可夫模型的特点决定了它不仅可清楚地表达出系统的每一个状态在某一条件下的下一个的状态转移情况,也可清晰反映出系统现处于某一功能降级的状态下,经有效的维修处理后返回的状态,在各行各业得到极大认可与应用[2-11]。
然而,当针对状态数量较多的复杂系统建立马尔可夫模型时,会使得模型极为巨大,极易出现状态组合爆炸问题,这也是制约马尔可夫方法应用的一个重要因素。因此,研究设计一种应用于复杂系统的马尔可夫模型构建简化方法是目前急需解决的问题。
为解决核电厂DCS 建立马尔可夫模型时容易出现组合爆炸问题,本研究提出一种应用于复杂系统的马尔可夫模型构建简化方法。进一步地,通过选取1oo2 架构作为实施案例,对提出的简化方法进行应用验证。
1 同类项筛查
如图1 所示,在对复杂系统进行分析时发现,系统实际运行过程中,不同设备在同一故障模式下对系统变量的影响相同,对下一级(系统)的影响也相同。在以往马尔可夫模型的建立过程中,需对每种设备的不同故障模式进行状态转移的建立。因此,传统的马尔可夫模型往往会出现组合爆炸的问题。本研究中,可对此种情况进行简化,分析设备或系统状态,将设备作为一个整体,根据其外部系统的影响情况进行划分,合并影响相同或近似的状态。

图1 复杂系统马尔可夫模型Fig.1 Markov model of complex system
首先,通过对马尔可夫模型中的状态进行检测,筛选出具有相同转移率的状态后组成简化状态组。简化状态组之间相互独立,且每个简化状态组中的成员数量不低于两个。其中,不同状态进入的概率相同,同时不同状态转移出去的概率相同,即为具有相同转移率的状态。
状态2 的转移率计算具体为:
其中,P2(t+Δt)为系统在t+Δt时刻处于状态2 的概率;P2(t)表示在时刻t 的状态2 的概率;λ表示失效率。
以此类推,对于状态n 的转移率可以得到:
式(2)中,Pn(t+Δt)为复杂系统在t+Δt时刻处于状态n 的概率;Pn(t)为复杂系统在t 时刻处于状态n 的概率;P1(t)为复杂系统在t 时刻处于状态1 的概率,λn-1Δt为复杂系统状态1 到状态n 的转移概率;λΔt为复杂系统状态2 到状态n+1 的转移概率。
2 状态合并原则
通过对马尔可夫模型中的状态进行检测,将符合要求的简化状态组中的成员状态以进入率相加、退出率保持不变的原则合并简化成一个状态。通过该状态合并原则,可以将多个状态合并为一个状态,减少马尔可夫模型的状态数量,从而达到简化效果。
简化状态组的合并简化计算具体为:
公式(3)验证了当多个状态具有相同的转换率时,多个状态就可以合并为一个状态,进入率相加,退出率保持不变。
3 简化模型可靠性评估
拒动概率是核电厂数字化仪控系统的一个重要可靠性指标要求。在IEC 61508 以及其他相关文献[11,12]中提出,对核电厂数字化仪控系统进行可靠性评估时,可以采用平均需求时失效概率PFDavg(Average Probability of a dangerous Failure on Demand)对系统拒动概率进行表征。
根据马尔可夫法的求解原理,当应用马尔可夫模型对核电厂数字化仪控系统PFDavg 进行求解时,首先需给定系统的初始矩阵P’如式(4)所示,即表示系统处于状态0。
式(4)表示系统在初始时刻处于第一个状态的概率为1。
然后,可以通过设置马尔可夫步长Δt=1h 来继续对马尔可夫相关解析式进行求解。通过式(4),可以推断出核电厂数字化仪控系统处于第n 小时的状态转移矩阵Pn,如式(5)所示。
式(5)中,转移矩阵Pn中各列对应的概率为系统第n 小时时所处该列对应状态的概率;P为根据马尔可夫模型求解得出的马尔可夫状态转移矩阵。因此,可求得核电厂数字化仪控系统处于拒动状态时,对应的第n 小时需求时失效概率PFDn。
最后,通过对PFDn 进行时间0 ~t 上的积分,再将积分结果进行t 等分,即可得到核电厂数字化仪控系统对应第n 小时时的平均失效概率PFDavg,如式(6)所示。
4 实例分析
4.1 模型建立及简化
假设某核电厂反应堆数字化仪控系统采取如图2 所示1oo2 架构,该架构由两个通道并联组成,任意一个通道都能执行安全功能,且只要有任意一个通道执行了安全功能,系统安全功能正常。因此,当且仅当两个通道都发生危险失效时,需求时安全功能才会失效。
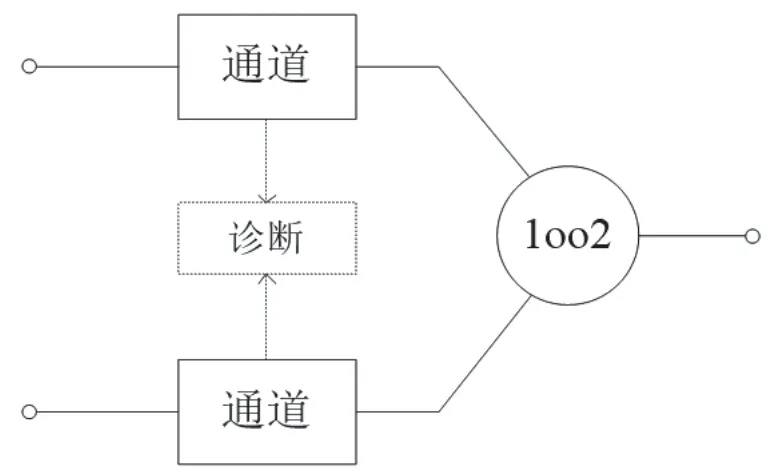
图2 1oo2系统结构框图Fig.2 The system block diagram of 1oo2
如图3 所示,根据1oo2 系统架构,按照传统的马尔可夫模型进行系统模型建立,得到马尔可夫模型。核电厂数字化仪控系统起始于状态0,该状态表示系统处于正常工作状态。当通道1 或者通道2 发生DDN(Dangerous Detected No-common-cause failure,危险可检测非共因失效)时,系统由状态0 转移到状态1 或者状态3;当通道1或者通道2 发生DUN(Dangerous Undetected No-commoncause failure,危险不可检测非共因失效)时,系统由状态0 转移到状态2 或者状态4;当发生SN(Safe No-commoncause failure,安全非共因失效)或者SC(Safe Commoncause failure,安全共因失效)时,系统将直接转移到最终状态5,即系统发生FS(Failure of Safe,安全失效);当发生DDC(Dangerous Detected Common-cause failure,危险可检测共因失效)时,系统将直接转移到状态6,即系统发生FDD(Failure of Dangerous Detected,危险可检测失效);当发生DUC(Dangerous Undetected Common-cause failure,危险不可检测共因失效)时,系统将直接转移到状态7,即系统发生FDU(Failure of Dangerous Undetected,危险可检测失效)。
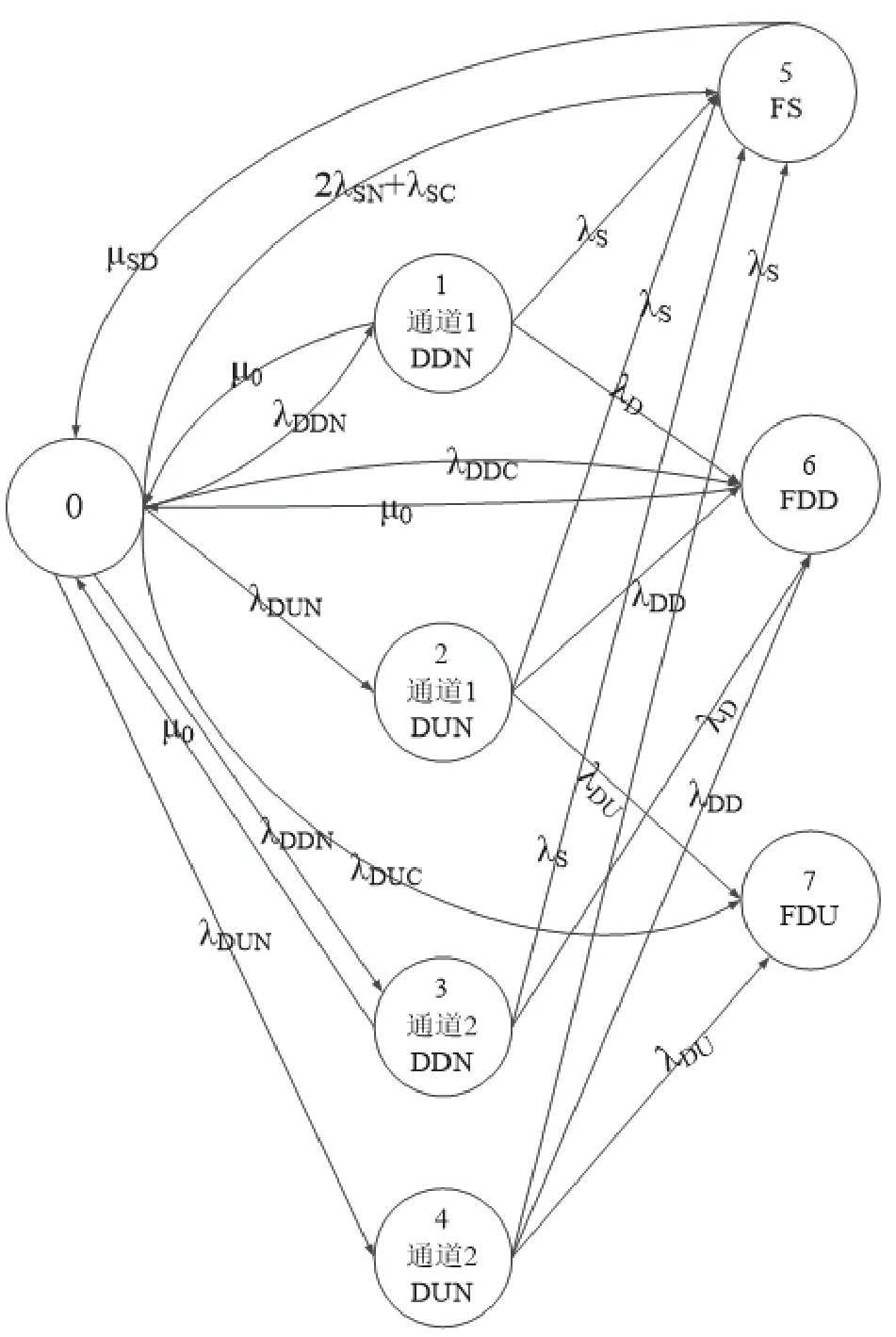
图3 传统的1oo2结构马尔可夫模型Fig.3 Traditional Markov model of 1oo2 structure
当系统处于状态1 或者状态3 时,只要有任一通道再发生S(Safe failure,安全失效),系统将转移到状态5;只要有任一通道再发生D(Dangerous failure,危险失效),系统将转移到状态6。
当系统处于状态2 或者状态4 时,只要有任一通道再发生S,系统将转移到状态5;只要有任一通道再发生DD(Dangerous Detected failure,危险可检测失效),系统将转移到状态6;只要有任一通道再发生DU(Dangerous Undetected failure,危险不可检测失效),系统将转移到状态7。
μ0 表示系统维修率,在状态转移模型中,当系统发生可检测失效时,可通过维修使得系统返回到状态0,对应的转移率用μ0 表示;λ 表示失效率,通过不同下角标用于表示单通道发生不同失效所对应的失效率。
通过图3 所示核电厂数字化仪控系统传统马尔可夫模型,可以得到其对应的状态转移矩阵P0,矩阵中首行首列为第0 行第0 列,然后依次展开,对应不同状态之间的转移率。如:第0 行第1 列表示系统从状态0 转移到状态1的转移率,以此类推。通过观察发现,通过传统的马尔可夫模型得到的状态转移矩阵P0为一个8 阶状态转移矩阵。
此时,应用本文提到的简化方法对建立的传统马尔可夫模型进行简化。
首先,筛选符合同类合并要求的相关状态。对图3 所示传统的1oo2 架构马尔可夫模型分析可知,状态1 与状态3 具有相同的转移率,即进入状态1 和状态3 的概率相同,从状态1 和状态3 转移出去的概率相同,满足所提出的简化原则。同理可知,状态2 与状态4 同样满足所提出的简化原则。
然后,应用同类合并简化原则对找到的状态1 和状态3、状态2 和状态4 进行状态合并,以达到简化马尔可夫模型的效果。如图4 所示,根据所提出的简化原则,状态1与状态3、状态2 与状态4 分别满足简化原则,对其进行简化合并,即“同类合并”。将状态1 与状态3 合并为一个状态,输入率相加,输出率保持不变;将状态2 与状态4合并为一个状态,输入率相加,输出率保持不变,对应状态转移概率矩阵为P,具体为:

图4 “同类合并”简化后的1oo2结构马尔可夫模型Fig.4 Markov model of 1oo2 structure after simplified"like-kind merger"
通过对比图3 所示的简化前马尔可夫模型和图4 所示简化后的马尔可夫模型以及简化前的状态转移矩阵P0和简化后的状态转移矩阵P可知,运用本文提出的马尔可夫模型简化方法,将原本8 阶模型矩阵简化到6 阶模型矩阵。
此实施例只是针对简单的1oo2 架构,通过实际应用可知,当运用到更加复杂的系统时,简化效果将非常明显。不同结构采用本文中提出的简化方法与传统方法之间马尔可夫状态转移矩阵模型大小对比见表1。
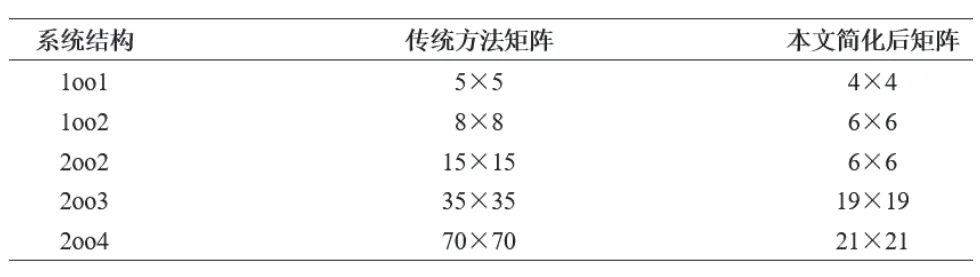
表1 传统方法与本文方法状态转移矩阵模型大小对比Table 1 Comparison of the size of the state transition matrix model between the traditional method and the proposed method
4.2 模型可靠性评估
假设该核电厂数字化仪控系统1oo2 架构中:故障诊断覆盖率DC(Diagnostic Coverage)=95%,系统故障重启时间FRT(Fault Restart Time)=24h,平均维修时间MTTR(Mean Time To Repair)=4h,共因因子β=1.5%,系统定期试验周期PTC(Periodic Test Cycle)=18 个月。
通道失效数据依据SN 29500 电子产品预计手册标准,可得到对应失效数据λ 为:通道安全失效率λS=515FIT,通道危险失效率λD=438FIT。将相关假设数据代入到简化后1oo2 马尔可夫转移矩阵P中,得到:
通过公式(4)、公式(5)以及公式(6)推导得出的应用马尔可夫模型求解系统平均需求时失效概率PFDavg 的可靠性评估方法,可得PFDavg=5.069×10-13。
5 结论
本文提出了一种应用于复杂系统的马尔可夫模型构建简化方法,解决了现有复杂系统建立马尔可夫模型时出现组合爆炸问题。通过对马尔可夫模型中的状态进行检测,筛选出具有相同转移率的状态后组成简化状态组,将简化状态组中的成员状态以进入率相加、退出率保持不变的原则合并简化成一个状态。通过合并同类状态的方法来减少马尔可夫模型状态或状态组以及对应的状态转移矩阵,以此达到简化马尔可夫模型的效果。
本文提出的马尔可夫模型简化方法,可以在核电厂数字化仪控系统马尔可夫模型建立过程中,极大降低系统状态数量以及状态转移矩阵阶数,以此减少马尔可夫模型建模以及计算维度,使得采用马尔可夫法用于核电厂数字化仪控系统可靠性评估工程应用成为可能,并为核电厂数字化仪控系统可靠性评估提供参考。

